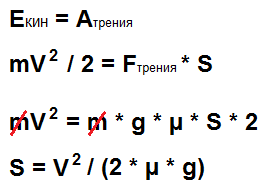Чем больше масса тем больше скорость
Вес тела и бег, как масса бегуна влияет на скорость и технику, расчёт влияния веса на скорость бега
Каким должен быть идеальный вес у бегуна для длинных и коротких дистанций?
Отвечает тренер по бегу.
Самый быстрый марафонец мира и дважды победитель Олимпийских игр Элиуд Кипчоге при росте 167 см весит 52 кг. Это единственный на сегодня человек, пробежавший марафонскую дистанцию в 42 195 м быстрее двух часов. В то же время Усэйн Болт – самый знаменитый спринтер – при росте 195 см весит 94 кг, то есть почти в два раза тяжелее Кипчоге. И оба – лучшие на своих дистанциях. Какой же вес тогда идеален для бегуна и влияет ли он на скорость бега?
На чемпионатах мира и Олимпийских играх нет ни одного атлета с заметной прослойкой жира под кожей.
Влияет ли вес на скорость?
Это зависит от продолжительности бега. Если вы спринтер и дистанция не больше 400 м, то мышцы будут очень интенсивно работать на протяжении нескольких десятков секунд. Такая работа требует большой мощности: спринтеры делают более 200 шагов в минуту, и каждый шаг двигает атлета вперёд на 2,2-2,4 м. Неудивительно, что в стартовые колодки на коротких дистанциях встают парни и девушки с мощными рельефными мышцами.
Александр: Спринтеры проводят много времени в тренажёрном зале, работая с большими отягощениями. В противном случае у них не получается выработать взрывную силу, необходимую для очень быстрого бега. Если же вы бежите 42 км, то главным для вас будет сбережение энергии. Элита марафонского бега делает 180-190 шагов в минуту, каждый длиной 1,6-1,9 м. Среди лучших марафонцев нет людей с большими мышцами, они очень сухие. То есть чем меньше веса вы несёте, тем меньше энергии потратите.
Проще говоря, есть две общие закономерности, связывающие массу тела и скорость бегуна:
Существует ли идеальный соревновательный вес бегуна?
Любой атлет, всерьёз стремящийся к достижению лучших результатов в беге, стремится достичь своего оптимального веса. А именно – сочетание максимально возможной мышечной массы (главным образом, мышц ног) и минимально возможной общей массы тела. Все бегуны – и спринтеры, и стайеры – хотят избавиться от жира, который мешает им бежать быстрее и дольше. И это неудивительно. Для обычных людей, которые бегают в своё удовольствие, контролировать массу тела тоже важно.
Как рассчитать свой идеальный вес для бега?
Александр: Общеизвестное правило «идеальный вес = рост минус 100» вполне работает с поправкой на телосложение. Тем, кому от папы с мамой достались небольшой рост и коренастая фигура, может хватить и формулы «рост минус 90». Но только если при этом кожная складка на животе совсем тоненькая и рельеф мышц живота (те самые «кубики») хорошо виден. Часто такие люди склонны к набору веса, поэтому им нужно регулярно вставать на весы и внимательно контролировать содержимое холодильника. Их тренировки, как правило, должны быть направлены на развитие и поддержание выносливости.
И наоборот, обладателям длинных тонких рук и ног могут понадобиться дополнительные усилия по наращиванию и поддержанию достаточной мышечной массы. Это нужно для того, чтобы справляться с нагрузками во время беговых тренировок и соревнований. У людей с таким типом фигуры чаще всего не возникает проблем с выносливостью. Но без работы на развитие силы им не хватает скорости.
В любом случае, какая бы фигура у вас ни была и как бы вы ни бегали, главное – продолжать тренироваться, поддерживать физическую активность и получать от этого удовольствие.
Второй закон Ньютона (Расчёты Примеры)
Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.
В результате чего были выведена новая формула второго закона ньютона а = F /m,
Что такое второй закон Ньютона, масса и вес тела

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.
Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.
Ускорение от величины силы
I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.
Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at2) : 2 определим ускорение a.
Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку
Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m . Это отношение назовем массой тела.
Зависимость ускорения от массы
II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).
Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть
Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).
Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):
где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.
Результирующая сила F равна векторной сумме всех сил, приложенных к телу;
Следовательно, сила равна произведению массы на ускорение.
Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение
подставим это выражение в уравнение второго закона Ньютона. Получим
Что такое импульс
Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (т υ ).
Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)
Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содер жащегося в данной теле. Это определение несовершенно.
Из второго закона Ньютона вытекает следующее определение массы. Из равенства
видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость это го тела и наоборот.
Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.
Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:
где m — масса тела, движущегося со скоростью υ; m0 — масса этого же тела, находящегося в покое; с = 3 • 10 8 м/с скорость света в вакууме.
Проанализируем данное уравнение:
По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.
Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.
Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.
Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.
Масса тела с ростом скорости
Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.
Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.
Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).
Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ0 = 0) называется свободным падением.
Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.
Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.
Если Р — сила тяжести, m — масса, g — ус корение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м /с 2 ), то применяя второй закон динамики, получим
Выразим с помощью этой формулы веса двух различных тел. Тогда:
Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.
Задачи на второй закон ньютона
Дано:
m = 1000 кг
a = 1 м/с 2
Решение:
Запишем второй закон Ньютона :
F = 1000 кг • 1 м/с 2 = 1000 Н
Ответ: 1000 Н.
2. На мяч действует сила F = 70 Н, масса мяча m = 0,2 кг, найти его ускорение a.
Дано:
Найти:
Решение:
Запишем второй закон Ньютона :
Статья на тему Второй закон Ньютона
Похожие страницы:
Понравилась статья поделись ей
Конечно влияет чем больше вес, тем меньше скорость.
Нет. чем больше масса тем меньше
ускорение. Ускорение это скорость изменения
скорости. Если сила (действующая
на тело) одна и та же а масса
больше, значит тело будет
медленнее разгонятся, значит и
ускорение тела будет меньше.
это зависеть от человека)) ) Выносливость, переносимый
вес.
здесь нет корреляции. Скорость зависит от скорости нервных импульсов в мышце и ее эластичности и разумеется от ее силовой способности
конечно же, чем больше масса, тем сложнее ускоряться.
Если сравнивать полного и худого людей с одинаковыми мышечными массами, то обгонит 90% худой.
Чем больше масса, тем тяжелее её разогнать, слишком быстро бежать не получиться, а вот тормозить будет тяжко)
если вес в мышцах выражен то нет, если в жире то да)
если вы бегаете медленно, то вес НАЧИНАЕТ (тоесть вам ещё надо бегать около часа) только через час, но вместе с ним сжигается и мышачная масса. Если бегать прирывесть. То есть, 100М быстро, 200м медлено, 100м пройтись, вес начинает сжигатся сразу, с такой техникой надо бегать всего 15-20 минут. А так не влияет.
если ноги из правильного места растут, то даже при большом весе можно быстро бегать
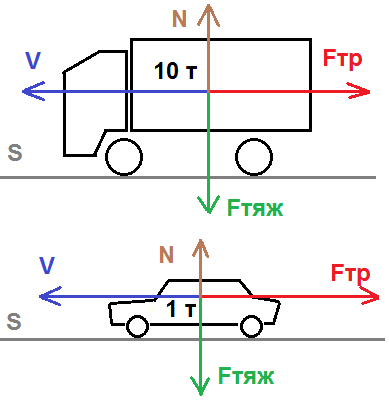
Конечно, ведь 10-тонная фура ездит быстрее 1-тонной легковушки (сарказм).
Смотря какой этот вес. Если жировой, то да. Если мышечный, то развитые накаченные ноги будут только в помощь на спринтерских дистанциях.
смотря от того, жирный ты или жилистый
Зависит ли тормозной путь от массы, или физика за 8 класс
Чтобы не отнимать время у членов ЛЛ, отвечаю сразу: нет, не зависит. Но дьявол как всегда кроется в деталях. Вообще говоря, жизненный опыт подсказывает нам, что тяжёлые предметы разогнать и остановить куда тяжелее, чем лёгкие. И вообще, если одновременно бросить камень и пёрышко, то камень приземлится на землю первым. Что же ты нам, ТС, втираешь? А мне сказать нечего – да, камень приземлится раньше пера. Это очевидно. Но только пока мы находимся в воздушном пространстве. Вспомните-ка опыт, который наверняка показывали в школе: в длинной стеклянной колбе находятся пёрышко и камушек. Пока колба заполнена воздухом, камень падает на дно колбы гораздо быстрее пера. Но стоит откачать воздух, как рвутся все наши шаблоны: перо и камень приземляются одновременно.
Ладно, ладно! Дураку понятно, что тут виной сопротивление воздуха. Но ведь всё равно камень же тяжелее пёрышка! Земля притягивает камень сильнее, чем перо. И с этим утверждением тоже трудно поспорить. Тогда какого чёрта они в вакууме падают одновременно? Масса-то у них разная! И вот тут нужно сделать одно важное отступление. Вообще говоря, в физике различают инертную массу и гравитационную. Так уж было угодно демиургам нашей вселенной, что они в точности совпадают, поэтому в жизни мы не делаем различия между этими видами масс. Килограмм – он и в Африке килограмм. Однако, различие заключается в проявлении этих масс. Инертная масса показывает, насколько тяжело вывести тело из состояния покоя (или равномерного прямолинейного движения, что в сущности, по заветам первого закона Ньютона, одно и то же). Представьте себе тяжёлый маятник, подвешенный на длинной нитке. Масса его, допустим, 1 тонна. Сможете ли вы раскачать его? Скорее всего да, но это будет очень тяжело и долго. Точно так же трудно будет вам и остановить такой маятник, если он будет раскачиваться. Вот она – инертная масса.
С гравитационной массой всё немного проще. Именно она определяет то, с какой силой все тела притягиваются к Земле (ну а в общем случае то, как сильно тянутся друг к другу любые два тела в пространстве). И если 1000-килограммовый маятник вы хоть и с трудом, но сдвинуть в воздухе сможете, то приподнять его даже на миллиметр не сможет никто. Даже втроём. Забавно, что окажись этот маятник на Луне, то три человека его вполне бы подняли. А вот раскачать этот маятник было бы точно так же тяжело, как и на Земле. И даже на борту МКС. Инертная сущность массы проявляется в том, что чем она больше, тем тяжелее ей придать какое-то ускорение. А гравитационное проявление массы связано с массой второго тела, к которому она притягивается (но поскольку 99,9999999% людей живут на Земле, то мы волей-неволей считаем вторым телом нашу hjlye. планету, и даже ввели константу g — ускорение свободного падения на Земле, с помощью которой отождествляем МАССУ тела и СИЛУ, с которой оно притягивается к Земле). Надеюсь, с видами масс разобрались.
Вернемся к камню и пёрышку. Почему же в вакууме они падают одновременно? А потому, что насколько сильнее камень притягивается к Земле, нежели пёрышко, настолько же тяжело ему сдвинуться из состояния покоя. Допустим, камень весит 100 грамм, а перо – 1 грамм. Чтобы разогнать более тяжёлый и инертный камень, нужна сила в 100 раз бОльшая, чем для пера. Но, с другой стороны, камень в 100 раз сильнее притягивается к Земле, нежели пёрышко. И вот оно – наглядное подтверждение равенства инертной и гравитационной массы тела.
Ну что за нудятина? И при чём тут торможение вообще? Где сравнение КамАЗа и легковушки? Спокойно! Сейчас всё будет!
Итак, на картинке у нас два автомобиля: первый давит на опору всеми своими 10 000 килограммами, а второй только 1 000 кг. При этом опора (дорога, асфальт) по третьему закону Ньютона отвечает автомобилям с точно такой же силой N, но направленной в противоположную сторону, т.е. вверх. Представим, что оба движутся с одинаковой скоростью V, например, 72 километра в час, что равняется 20 метрам в секунду. Едут они по одной и той же дороге. Дорога идеально ровная, сухой асфальт. И вот в один и тот же момент они резко бьют по тормозам, колёса идут юзом, и автомобили останавливаются. Давайте разбираться, что же при этом происходит.
Как мы помним из нашей любимой физики, движущееся тело обладает кинетической энергией. Численно она равна половине произведения массы на квадрат скорости (в коментах напишите, кто при встрече с бетонной стеной ухандокается сильнее: 1000-килограммовый седан на скорости 110 км/ч или же 2-тонный внедорожник на 75 км/ч?). А у остановившегося автомобиля кинетической энергии нет, ибо скорость нулевая. Но мы же помним, что энергия просто так никуда не пропадает, она лишь переходит из одного вида в другой. Куда же перешла вся кинетическая энергия при торможении? А перешла она в тепловую – асфальт и шины тупо нагрелись. И заставила их нагреться сила трения Fтр. При этом, до момента торможения автомобиль проходит какой-то путь S. Таким образом, сила трения (которая зависит от массы m, ускорения свободного падения g и коэффициента трения µ) совершает работу по остановке автомобиля, равную произведению силы трения на это расстояние. И, поскольку вся кинетическая энергия пошла на работу по нагреву шин и асфальта, мы их тупо приравниваем:
Как нетрудно заметить, в третьей строке у нас сократились массы в левой и правой части. Физический смысл такого сокращения описан выше – это эквивалентность инертной (в левой части) и гравитационной (в правой) масс. Чем сильнее разогнать массивное инертное тело, тем неохотнее оно будет останавливаться. С другой стороны, чем больше масса тела, тем сильнее оно прижимается к Земле, тем выше сила трения, которая тормозит эту массу. Таким образом, тормозной путь автомобиля зависит только от скорости и коэффициента трения µ.
НО! Всё вышесказанное справедливо только при условии, что дорога идеально ровная, и все колёса обоих сравниваемых автомобилей тормозят юзом. Впрочем, пока что информации хватит. Если тема покажется интересной, то обо всех этих нюансах и об отличиях теории от реалий поговорим в следующий раз.
Зависимость массы от скорости и Релятивистская масса.
Некоторым просто интересна физика, для других это любимый предмет в школе, остальные вовсе хотят понять как устроен окружающий мир, и некоторые из нас встречались с одним из самых популярных утверждениях в физике — «масса тела зависит от скорости».
1) Верность самого утверждения.
Кажется что ничего сложного нету, масса как масса, скорость как скорость, однако, люди которые разбираются в этой теме, сразу зададутся вопросом, про какую массу идет речь. Дело в том что в физике есть «инвариантная масса» (так же называемая «масса покоя») и «релятивистская масса», и собственно верность утверждения напрямую зависит от выбранной вами массой. Релятивистская масса тела растет с увеличением скорости тела, а вот масса покоя тела— нет. (Но если все же быть более точным, то ответ будет — нет, так как под массой в современной физике подразумевается именно инвариантная масса, а термин релятивистская масса уже просто не актуален.)
2) Масса покоя/Инвариантная масса.
Масса покоя и инвариантная масса это самая обыкновенная масса, с которой мы знакомы еще со школы.
Масса в Ньютоновской механике:
1. Масса является мерой количества вещества, количества материи.
2. Масса составного тела равна сумме масс составляющих его тел.
3. Масса изолированной системы тел сохраняется, не меняется со временем.
4. Масса тела не меняется при переходе от одной системы отсчета к другой, в частности, она одинакова в различных инерциальных системах координат.
5. Масса тела является мерой его инертности (или инерции, или инерционности, как пишут некоторые авторы).
6. Массы тел являются источником их гравитационного притяжения друг к другу.
Масса в релятивистской механике Эйнштейна:
СТО и ОТО были прорывом в понимании нашего мира. Теория относительности — физическая теория пространства-времени, то есть теория, описывающая универсальные пространственно-временные свойства физических процессов.
Релятивистская теория (Теория относительности) в отличии Ньютоновской механики (т.е. нерелятивистской) учитывает предельную скорость для распространения информации c = 3 · 10^8 м/с (скорость электромагнитной волны в вакууме), кроме того, Эйнштейн изменил фундаментальные взгляды на время и пространство.
Наиболее строгое определение массы даётся в специальной теории относительности (СТО): масса — это абсолютная величина 4-вектора энергии-импульса:
Основными соотношениями теории относительности для свободно движущейся частицы (системы частиц, тела) являются:
Где E — энергия, p — импульс, m — масса, v — скорость частицы (системы частиц, тела), здесь масса и скорость те же самые величины знакомые нам с Ньютоновской механики.
Подобно четырехмерным координатам t, r, энергия E и импульс p являются компонентами четырехмерного вектора. Они меняются при переходе от одной инерциальной системы к другой согласно преобразованиям Лоренца. Масса же остается при этом неизменной, она является лоренцевым инвариантом. Как и в ньютоновой механике, так и в теории относительности справедлив законы сохранения энергии и импульса для изолированной частицы или изолированной системы частиц, кроме того, как и в ньютоновой механике, энергия и импульс аддитивны.
Что касается массы, то в теории относительности масса изолированной системы сохраняется, не меняется со временем, но свойством аддитивности не обладает. Одним из важнейших отличий релятивистской механики от ньютоновской является то, что энергия тела (обладающей массой) не равна нулю даже когда такое тело покоится (т. е. при v = 0, p = 0). Это видно из одной из самых популярных формул Эйнштейна и физики в целом:
Замечательным свойством уравнений (2.2) и (2.3) является то, что они описывают движение частиц во всем интервале скоростей: 0 ⩽ v ⩽ c. В частности, при v = c из (2.3) следует, что:
Подставив это равенство в (2.2), мы приходим к выводу, что если частица движется со скоростью с, то ее масса равна нулю, и наоборот. У безмассовой частицы нет системы координат, где она покоится.
Для массивных частиц (все частицы с ненулевой массой) формулы для энергии и импульса удобно выразить через массу и скорость. Для этого подставим (2.3) в (2.2):
Извлекая квадратный корень, получим:
Подставляя (2.7) в (2.3), получим:
Из формул (2.7) и (2.8) очевидно, что массивное тело (с массой не равной нулю) не может двигаться со скоростью света, так как при этом должны обратиться в бесконечность энергия и импульс тела.
В литературе по теории относительности обычно используются обозначения:
Используя γ, можно записать E и p в виде:
Определим кинетическую энергию Е(кин) как разность полной энергии E и энергии покоя E(0):
В пределе, когда v/c ≪ 1, в выражениях (2.12), (2.13) следует оставить первые члены ряда по β. Тогда мы естественным образом возвращаемся к формулам механики Ньютона:
Откуда видно, что масса тела в Ньютоновой механике и масса того же тела в релятивистской механике — это одна и та же величина.
Что в итоге мы имеем?
1). В релятивистской механике материя имеет более фундаментальное понятие, чем в Ньютоновской, нет принципиальной разницы между веществом (протонами, нейтронами, электронами и т.д.), т.е. масса не является мерой количества материи.
2). Масса систем частиц зависит не только от количества составных частиц, но и от энергий этих частиц и связей создаваемых между частицами, в нерелятивистской механике чем больше отдельных частиц тем больше масса системы, однако в релятивистской механике масса составного тела не равна сумме масс составляющих его тел.
3). Как и в Ньютоновой механике, масса изолированной системы тел сохраняется, не меняется со временем. Только теперь, разумеется, в число этих тел необходимо включить не только «вещество», скажем атомы, но и «излучение» (фотоны).
4). Как и в Ньютоновой механике, в теории относительности масса тела не меняется при переходе от одной инерциальной системы отсчета к другой.
5). Масса релятивистски движущегося тела не является мерой его инертности. Более того, единой меры инертности для релятивистски движущихся тел вообще не существует, поскольку сопротивление тела ускоряющей его силе зависит от угла между силой и скоростью.
6). Масса релятивистски движущегося тела не определяет его взаимодействия с гравитационным полем. Это взаимодействие определяется выражением, зависящим от энергии и импульса тела
7). Согласно теории относительности масса частицы является мерой энергии, заложенной в покоящейся частице. Это свойство массы было неизвестно в нерелятивистской механике.
3) Откуда пошла зависимость массы и скорости?
Думаю все мы встречались с знаменитой формулой Эйнштейна:
Согласно формуле 3.1 любое тело с энергией Е имеет массу равную Е/с², с другой стороны по формуле 3.2 масса m имеет в себе заложенную покоящуюся энергию Е(0), кроме того по формуле 3.1 фотон обладает массой, а по формуле 3.2 фотон будет являться безмассовой частицей.
Формула 3.1 появилась еще до создания теории относительности (в 1900г), автор формулы А. Пуанкаре. За год до появления формулы 3.1 Лоренц впервые ввел понятие продольной и поперечной масс ионов.
В итоге получилось что до создания теории относительности уже существовало три массы, которые растут вместе с энергией тела, это:
Физикам так же пришлось ввести четвертую массу — массу покоя, этот термин обозначал простую массу, которую по началу обозначали m(0), но в последствие в теории относительности стали обозначать как m. Так и получилась «банда четырех» которой удалось успешно внедриться в рождающуюся теорию относительности, в итоге создав путаницу по сей день.
4) Релятивистская масса.
Термин релятивистская масса так и остался в физике, само введение этого понятия не дало никаких новых возможностей для физиков, в общем это просто энергия тела поделенная на скорость света в квадрате. Последнее десятилетия все физики в основном используют только лоренц-инвариантную массу (масса покоя, инвариантную масса).
К сожалению релятивистская масса продолжает встречаться в учебниках, в школьных программах, в научно-популярном контенте, это не просто живучий педагогический вирус, это иногда и реальный вред, пустое понятие в физике.
Понятие релятивистской массы не только пустое в научном смысле, но и вредное — в педагогическом. Масса, растущая со скоростью, формирует у человека яркое, интуитивно привлекательное, но неправильное понимание явлений, развивает неправильную физическую интуицию. Если человек собирается заниматься физикой всерьез, то ему всё равно придется переучиться. Но даже если не собирается, эта интуиция будет постоянно ему подсовывать неверное толкование некоторых физических ситуаций. Вот несколько примеров, когда интуиция, основанная на релятивистской массе, приводит к неправильному предсказанию или к не состыковке с другими физическими утверждениями.
СТО и ОТО на данный момент полностью самосогласованные теории, прекрасные и идеальные, а такая путаница в терминологии может не просто запутать человека который пытается ее понять, но и вовсе построить неверное представление о физике.
5) Некоторые вытекающие вопросы и утверждения.
Термин релятивистская масса процветает именно в научно-популярной сфере, нежели в чисто научной, сами ученные не путаются, они все между собой договорились, они все прекрасно понимают что подразумевается под массой, а вот любители нет. Вследствие этого, у некоторых могут возникнуть следующие вопросы, или заблуждения.
1) Невозможно двигаться со скоростью света (именно массивному объекту), так как чем ближе приближаемся к скорости света, тем масса тела больше, соответственно она стремится к бесконечности.
Нет, масса тела не растет со скоростью. На самом деле массивные объекты не могут двигаться со скоростью света из за взаимодействия с полем Хиггса. Необходимо передать бесконечное количество энергии что бы добраться до скорости света, что в общем-то и не возможно.
2) Фотон имеет массу, которую мы можем найти через формулу релятивистской массы.
Нет, фотон не то что массой не обладает, но и размерами. Именно благодаря тому что фотон безмассовая частица, он и может двигаться со скоростью света, при чем в любой системе координат его скорость будет постоянной.
3) У всех ли одного типа частиц одинаковая масса?
Да, у всех протонов одна и та же масса, у всех электронов одинаковая масса, у всех нейтронов одинаковая масса и так далее.
4) Масса электрона может быть больше массы ядра, так как электрон двигается с высокой скоростью.
Нет. Масса электрона никак не зависит от его скорости.
5) Тело двигаясь с около световой скоростью может стать черной дырой, так масса тела растет, а продольный размер сокращается, то значит, рано или поздно радиус Шварцшильда превысит размер тела.
Нет. Тело не в коем случае не может стать черной дырой таким образом.
6) Статья К. Адлера опубликованная в «Американском журнале физики» в 1987 г.
В данной статье рассказывается о случае, когда сын автора статьи спрашивает у отца — «Папа, а масса действительно зависит от скорости?», Ответ был — «Нет!». «Впрочем, да», «На самом деле нет, но не говори об этом своему учителю». На следующий день сын прекратил заниматься физикой.
7) Где же встречается релятивистская масса?
Не только интернет, но даже и книжные издания распространяют термин релятивистской массы. Например в YouTube, канал QWERTY, видео «Теория относительности для чайников (часть 1)»: