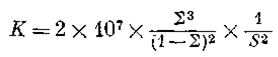Чем больше пористость тем больше проницаемость

Зависимость проницаемости от пористости

Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеально пористой среды оценивается из соотношения уравнений Пуазейля и Дарси. В этом случае пористая среда представляется в виде системы прямых трубок одинакового сечения длиной L, равной длине пористой среды.

Уравнение Пуазейля описывает объёмную скорость течения жидкости через такую пористую среду:

, (1.22)

где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

F – площадь фильтрации;

m – вязкость жидкости;

DР – перепад давлений.

Коэффициент пористости среды, через которую проходит фильтрация:

. (1.23)

Следовательно, уравнение (1.22) можно переписать следующим образом:

. (1.24)

Из уравнения Дарси следует, что:

. (1.25)

Приравняв правые части уравнений (1.24) и (1.25) получим взаимосвязь пористости и проницаемости:

. (1.26)

Из чего следует, что размер порового канала будет равен:

. (1.27)

. (1.28)

Для реальных условий используется эмпирическое уравнение Ф.И. Котякова:

, (1.29)

j – структурный коэффициент, описывающий извилистость порового пространства.

Значение j можно оценить путём измерения электросопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, j изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

. (1.30)

Для оценки коэффициента проницаемости при фильтрации через каналы используются соотношения уравнений Пуазейля и Дарси.

и . (1.31)

Подставив эту величину в уравнение Пуазейля и сократив одинаковые параметры в (1.29) получим:

. (1.32)

Оценка проницаемости для фильтрации через трещиноватые поры оценивается из соотношения уравнений Букингема и Дарси.

Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

, (1.34)

где h – высота трещины;

v – линейная скорость фильтрации.

Подставив это выражение в уравнение Дарси, получим:

. (1.35)

Виды проницаемости

Проницаемость абсолютная (физическая) – проницаемость пористой среды для газа или однородной жидкости при следующих условиях:

1. Отсутствие физико-химического взаимодействия между пористой средой и этим газом или жидкостью.

2. Полное заполнение всех пор среды этим газом или жидкостью.

Для продуктивных нефтяных пластов эти условия не выполняются.

Проницаемость фазовая (эффективная) – проницаемость пористой среды для данного газа или жидкости при одновременном наличии в порах другой фазы или системы (газ-нефть, газ-нефть-вода).

При фильтрации смесей коэффициент фазовой проницаемости намного меньше абсолютной проницаемости и неодинаков для пласта в целом.

Относительная проницаемость – отношение фазовой проницаемости к абсолютной.

Проницаемость горной породы зависит от степени насыщения породы флюидами, соотношения фаз, физико-химических свойств породы и флюидов.

Фазовая и относительная проницаемости для различных фаз зависят от нефте-, газо- и водонасыщенности порового пространства породы, градиента давления, физико-химических свойств жидкостей и пористых фаз.

Насыщенность– ещё один важный параметр продуктивных пластов, тесно связанный с фазовой проницаемостью.

Предполагается, что продуктивные пласты сначала были насыщены водой. Водой были заполнены капилляры, трещины, каналы.

При миграции углеводороды, вследствие меньшей плотности, стремятся к верхней части пласта, выдавливая вниз воду. Вода легче всего уходит из трещин и каналов, из капилляров вода не уходит в силу капиллярных явлений. Таким образом, в пласте остаётся связанная вода.

Чтобы определить количество углеводородов, содержащихся в продуктивном пласте, необходимо определить насыщенность порового пространства породы нефтью, водой и газом.

Водонасыщенность S_В – отношение объёма открытых пор, заполненных водой к общему объёму пор горной породы. Аналогично определение нефте- и газонасыщенности:

. (1.37)

Обычно для нефтяных месторождений S_В = 6-35%; S_Н = 65-94%, в зависимости от созревания пласта.

Для нефтяных месторождений справедливо следующее соотношение:

Для газонефтяных месторождений:

Пласт считается созревшим для разработки, если остаточная водонасы­щенность S_В

Источник

Зависимость проницаемости от пористости. Теоретически доказано, что для хорошо отсортированного, окатанного, однородного материала (например

Теоретически доказано, что для хорошо отсортированного, окатанного, однородного материала (например, кварцевый мономиктовый песок, представленный на 90 % одним минералом) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются и более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеальной пористой среды можно оценить из соотношений законов Пуазейля и Дарси.

Уравнение Пуазейля описывает объёмную скорость течения жидкости через пористую среду, которая представляется в виде системы прямых трубок одинакового сечения длиной (L), равной длине пористой среды:

, (1.25)

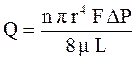
где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

F – площадь фильтрации;

m – вязкость жидкости;

DР – перепад давления.

Коэффициент пористости среды, через которую проходит фильтрация, можно представить следующим образом:

. (1.26)

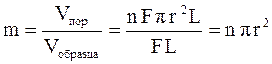
С учетом 1.26, уравнение 1.25 можно переписать следующим образом:

, (1.27)

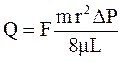
и сравнить его с уравнением Дарси ( ).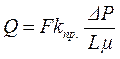

Приравняв правые части уравнений, после сокращения подобных членов получим выражение для взаимосвязи проницаемости, пористости и радиуса порового канала:

. (1.28)

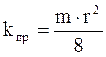
Выражение 1.28 используется при проведении прогнозных и модельных расчетах коэффициента проницаемости для образцов кернового материала с известной пористостью. Измерения показали, что радиусы пор, по которым в основном происходит движение жидкостей, находится в пределах от 5 до 30 мкм.

Из уравнения 1.28 следует, что радиус (размер) порового канала можно оценить:

. (1.29)

. (1.30)

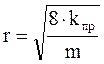
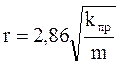
Уравнения 1.28-1.30 характеризуют взаимосвязь между пористостью, проницаемостью и радиусом порового канала и справедливы только для идеальной пористой среды, например, для кварцевого песка.

Для реальных коллекторов оценка радиуса порового канала производится с учётом структурных особенностей порового пространства пород. Обобщенным выражением для этих целей является эмпирическое уравнение Ф.И. Котяхова:

, (1.31)

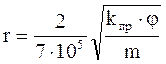
j – структурный коэффициент, учитывающий извилистость порового пространства.

Значение j оценивают для модельных сред путём измерения электрического сопротивления пород. Для керамических, пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, j изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

. (1.32)

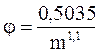
Для оценки взаимосвязи коэффициента проницаемости от радиуса порового каналапри фильтрации жидкости только через каналы, капилляры (поры круглого сечения) используются соотношения уравнений Пуазейля и Дарси:

и . (1.33)

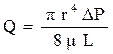
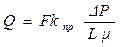
Причем, пористая среда представляет собой систему трубок. Общая площадь пор, через которые идет фильтрация флюидов, оценивается как:

.(1.34)

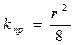
Оценка взаимосвязи коэффициента проницаемости от высоты поровой трещиныпри фильтрации жидкости только через трещиноватые поры оценивается из соотношений уравнений Букингема и Дарси.

Потеря давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

, (1.36)

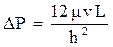
где h – высота трещины;

v – линейная скорость фильтрации жидкости.

Выразив из уравнения Дарси величину перепада давления (∆P = v·μ·L/k_пр.), приравняв правые части с 1.36 и сократив одинаковые параметры получим выражение:

. (1.37)

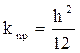
Уравнения 1.35 и 1.38 используется для теоретической оценки коэффициентов проницаемости для конкретного вида пор.

Рассмотрим пример.Через кубик породы размером 10·10·10 см, с проницаемостью 10 мД фильтруется жидкость при линейной режиме вязкостью 1 спз, при градиенте давления (∆Р/∆L), равном 0,25 атм/м (0,0025 атм/см). Определить дебит?

Решение. Рассмотренный случай – субкапиллярной фильтрации, то есть фильтрация равномерная и проходит через всю площадь образца, имеющего субкапиллярную пористость. Дебит (Q₁)составит:

= 100 · 0,01 · (0,0025 /1) = 0,0025 см 3 /сек.

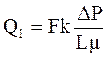
Если в этом кубике будет один канал диаметром 0,2 мм той же длины, что и кубик, то при том же градиенте давления дебит фильтрующейся жидкости через этот канал будет:

= 12,5 · 10 6 · (0,02 /2) 2 · π · (0,02 /2) 2 · 0,00025 = 0, 001 см 3 /сек

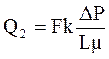
Следовательно, при наличии в кубике одного канала и субкапиллярной пористости, т. е. при наличии неравномерной фильтрации суммарный дебит (Q₃) фильтрующейся жидкости составит:

Q₃ = Q₂ + Q₁ = 0,001 + 0,0025 = 0,0035 (см 3 /сек).

Суммарный дебит (Q₃) имеет величину на 40 % больше чем при субкапиллярной фильтрации (Q₁).

Если в кубике вместо канала имеется трещина высотой 0,2 мм и шириной 10 см, ее влияние на общий дебит жидкости, фильтрующийся через породу, будет существенным:

= (84,4 ·10 5 · (0,02) 2 · 0,02 · 10 · 0,0025) / 1 = 1,688 см 3 /сек.

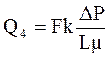
А суммарный дебит (Q₅) с учетом субкапиллярной фильтрации (Q₁) составит:

По сравнению с первым случаем дебит увеличится в 675 раз.

Пример свидетельствует о большом влиянии наличия каналов и особенно трещин в породе на объём фильтрующейся жидкости.

На практике проницаемость породы определяют в лабораторных условиях по керновому материалу (см. лабораторный практикум).

Источник

Связь между пористостью и проницаемостью

Связь между пористостью и проницаемостью

Количественная зависимость между пористостью и проницаемостью весьма

.

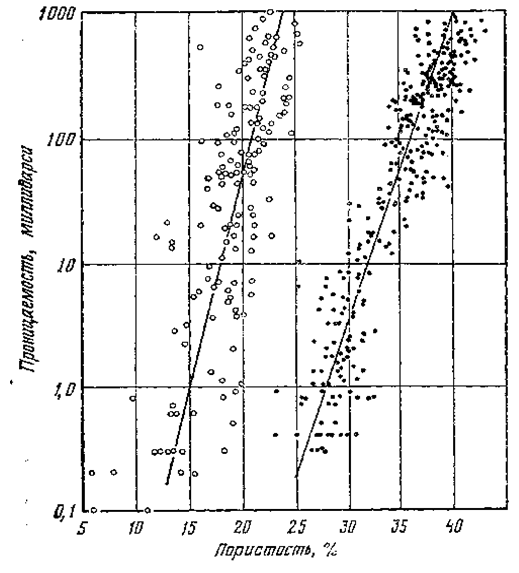
Рис. 1. Зависимость меду пористостью и проницаемостью в двух коллекторах: песчанике Верхний Уилкокс (эоцен) в Мерси, Техас (слева), и мелкозернистом песчанике Накаточ (верхний мел) в Белвью, Луизиана (справа) (Archie, Bull. Am. Assoc. Petrol. Geol., 34, p. 945, Fig. 1). Наблюдается общее увеличение проницаемости с увеличением пористости

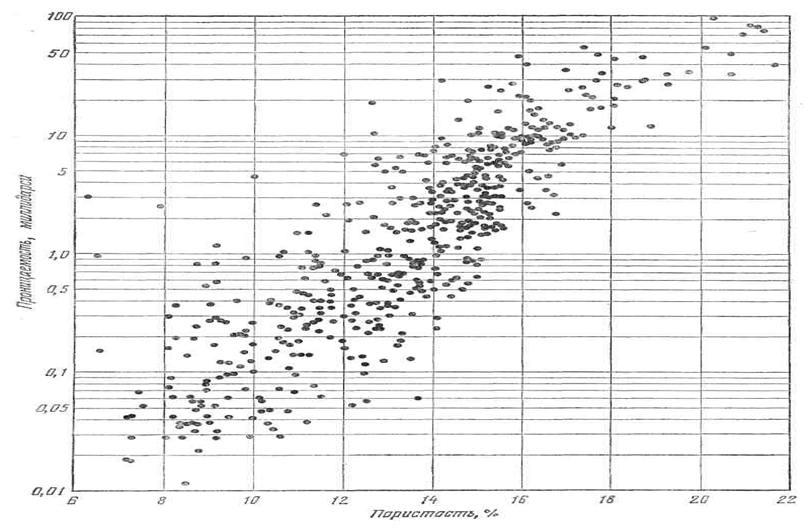
изменчива и трудно поддается определению. Помимо общеизвестного факта, что проницаемая порода должна быть также и пористой, между двумя ее свойствами, по-видимому, нет более тесной связи (рис. 1). Было произведено множество замеров пористости и проницаемости песчаников Брадфорд (нижний девон), Пенсильвания, которые в силу своей равномерной мелкозернистости, казалось, должны бы были характеризоваться достаточно постоянной зависимостью между этими параметрами, если она вообще существует. Однако, как видно из (рис. 2), даже в этих породах наблюдается лишь самая общая связь менаду ними. Влияние трещиноватости на пористость и проницаемость известняков и доломитов, установленное в результате обобщения данных нескольких сотен измерений, показано на (рис. 3). Линия К_90° (проницаемость перпендикулярно к системе трещин) отражает связь с первичной пористостью и кавернозной пористостью; линия К_макс отражает максимальную проницаемость пород в направлении, параллельном системе трещин. Проницаемость нетрещиноватых доломитов возрастает в обоих направлениях в соответствии с увеличением пористости. В то время как пористость является безразмерной величиной, проницаемость в соответствующих единицах измерения отражает сопротивлениепо роды прохождению через нее гомогенного флюида. Теоретически проницаемость может быть увязана с характером структуры горной породы согласно уравнению

Рис. 2. Значения пористости и проницаемости для 500 образцов песчаников Брадфорд (нижний девон) из месторождения Брадфорд в северо-западной Пенсильвании (Ryder, World Oil, p. 174, 1948).

Все образцы представляют собой колонки керна длиной в 1 фут, отобранные из 29 скважин, сосредоточенных на небольшой площади. Считается, что песчаник Брадфорд характеризуется эднородным строением, и на графике, несмотря на общее увеличение проницаемости с увеличением пористости, наблюдается широкий разброс точек, свидетельствующий об отсутствии тесной связи между пористостью и проницаемостью. Так, любому значению проницаемости соответствуют различные значения пористости (от 6 до 10 значений).

Эффективная пористость и проницаемость представляют собой основные свойства пород-коллекторов. Эффективная пористость обеспечивает пространство, в котором происходит скопление нефти и газа, а проницаемость способствует их миграции в породе.

Инженеры-промысловики и сотрудники лабораторий достигли больших успехов в понимании факторов, влияющих на пористость пород-коллекторов, особенно в выяснении роли глинистых частиц, действия различных пластовых вод и петрофизических свойств пустот различных типов. Собрана масса детальных количественных данных о пористости и проницаемости отдельных природных резервуаров, влиянии каждого из этих параметров на дебиты нефти и газа и взаимосвязи порового пространства с содержащимися в нем флюидами. Однако предстоит еще многое изучить, особенно в отношении совершенствования методов извлечения нефти из пород с чрезвычайно низкой пористостью и проницаемостью, влияния размеров зерен на пористость и проницаемость и связи различных видов пористости и проницаемости с обстановкой накопления осадков. Все это поможет лучше понять условия, существующие на глубинах, и повысить точность прогнозирования перспектив нефтегазоносности.

¹Такие коллекторы можно назвать техноколлекторами.

¹В карбонатных коллекторах эффективным является применение гидрокислотного разрыва, под действием которого наряду с образованием трещин и увеличением степени II раскрытия происходит и растворение отдельных компонентов породы.

Источник

Нефть, Газ и Энергетика

Блог о добычи нефти и газа, разработка и переработка и подготовка нефти и газа, тексты, статьи и литература, все посвящено углеводородам

Зависимость проницаемости от пористости

Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются и более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеальной пористой среды оценивается из соотношений уравнений Пуазейля и Дарси. В этом случае пористая среда представляется в виде системы прямых трубок одинакового сечения длиной L, равной длине пористой среды.

Уравнение Пуазейля описывает объёмную скорость течения жидкости через такую пористую среду:

где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

F – площадь фильтрации;

m – вязкость жидкости;

DР – перепад давлений.

Коэффициент пористости среды, через которую проходит фильтрация:

Следовательно, уравнение (1.20) можно переписать следующим образом:

Приравняв правые части уравнений (1.22) и (1.23) получим выражение для взаимосвязи пористости, проницаемости и радиуса порового канала:

Из чего следует, что размер порового канала можно оценить:

Если выразить проницаемость в мкм2, то радиус поровых каналов (в мкм) будет рассчитываться:

Для реальных коллекторов оценка радиуса порового канала производится с учетом структурных особенностей пород. Обобщенным выражением для этих целей является эмпирическое уравнение Ф.И. Котякова:

где r – радиус пор; j – структурный коэффициент, учитывающий извилистость порового пространства.

Значение j можно оценить путём измерения электрического сопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, j изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

Для оценки взаимосвязи коэффициента проницаемости от радиуса порового канала (при фильтрации жидкости только через каналы, капилляры) используются соотношения уравнений Пуазейля и Дарси.

Причем, пористая среда представляет собой систему трубок. Общая площадь пор через которые происходит фильтрация равна: F = π · r2, откуда π = F/ r2.

Подставив эту величину в уравнение Пуазейля и сократив одинаковые параметры в выражениях (1.29) получим:

Если r измеряется в [см], а коэффициент проницаемости в [Д] (1Д = 10-8см). то вводится соответствующий коэффициент пересчета = 9,869·10 –9. Тогда, коэффициент проницаемости при фильтрации жидкости через капилляр оценивается эмпирическим выражением:

Кпр = r2 / (8·9,869·10 –9) = 12,5 · 106 r2. (1.31)

Оценка взаимосвязи коэффициента проницаемости от высоты поровой трещины (для фильтрации жидкости только через трещиноватые поры) оценивается из соотношений уравнений Букингема и Дарси.

Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

где h – высота трещины; v – линейная скорость фильтрации.

Подставив это выражение в уравнение Дарси (1.23) и сократив подобные члены, получим:

С учетом того, что r измеряется в [см], а коэффициент проницаемости в [Д], вводим соответствующий коэффициент пересчета = 9,869·10 –9. Тогда, коэффициент проницаемости при фильтрации жидкости через трещину оценивается:

Кпр = h2 / (12 · 9,869·10 –9) = 84,4 · 105 h2. (1.34)

Уравнения (1.31) и (1.34) используется для теоретической оценки коэффициентов проницаемости для конкретного вида пор. На практике проницаемость породы определяют в лабораторных условиях по керновому материалу (см. раздел лаборат. практикума).

Источник

Документы

§ 6. ЗАВИСИМОСТЬ ПРОНИЦАЕМОСТИ ОТ ПОРИСТОСТИ И РАЗМЕРА ПОР

Прямой зависимости между проницаемостью и пористостью горных пород не существует. Например, трещиноватые известняки, имеющие малую пористость, часто обладают большой проницаемостью и, наоборот, глины, иногда характеризующиеся высокой пористостью, практически непроницаемы для жидкостей и газов, так как их поровое пространство слагается каналами субкапилляр-ного размера. Однако на основании среднестатистических данных можно сказать, что более проницаемые породы часто и более пористые 45 (рис. 1.10).

Проницаемость пористой среды зависит преимущественно от размера поровых каналов, из которых слагается поровое пространство. Поэтому изучению структуры, строения и размеров пор уделяется большое внимание.

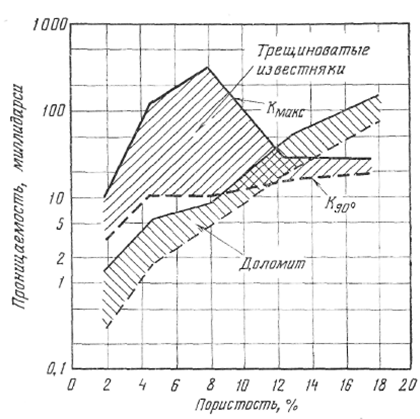
Зависимость проницаемости от размера пор можно получить путем приложения законов Дарси и Пуазейля к пористой среде, которую представим в виде системы трубок одинакового сечения. По закону Пуазейля расход Q жидкости через такую пористую среду составит

где п — число пор, приходящихся на единицу площади фильтрации;

R — радиус поровых каналов (или средний радиус пор среды);

Рис. 1.10. Зависимость между проницаемостью и пористостью пород двух коллекторов (по А. И. Леворсену). / — песчаник эоценового возраста; 2 — тонкозернистый песчаник мелового возраста.

F — площадь фильтрации;

Ар — перепад давления; ц — динамическая вязкость жидкости; L — длина пористой среды. Коэффициент пористости среды

Подставляя в формулу (1.14) вместо п nR 2 значение пористости т, получим

По закону Дарси расход жидкости через эту же пористую среду

Здесь к — проницаемость пористой среды. 28

Приравнивая правые части формул (1.17) и (1.16), получим

Если выразить проницаемость в дарси, то радиус поровых каналов R (в м) будет равен

Или, если R выразить в мкм, то

Величина Л, определенная по формуле (1.19), представляет собой радиус пор идеальной пористой среды, обладающей пористостью т и проницаемостью к. В приложении к реальной пористой среде величина R имеет условный смысл и не определяет среднего размера пор, так как не учитывает их извилистость и сложное строение.

По предложению Ф. И. Котяхова лучше вычислять средний радиус пор реальных пористых сред по эмпирической формуле

где ф — структурный коэффициент, характеризующий отличительные особенности строения порового пространства реальных коллекторов. Величину ф можно оценить путем измерения электросо

противления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28 по экспериментальным данным ф изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно определить также по эмпирической формуле

Другим широко применяемым методом исследования структуры и строения высокодисперсных пористых тел является экспериментальная порометрия — измерение размеров и характера распределения пор по размерам.

Источник