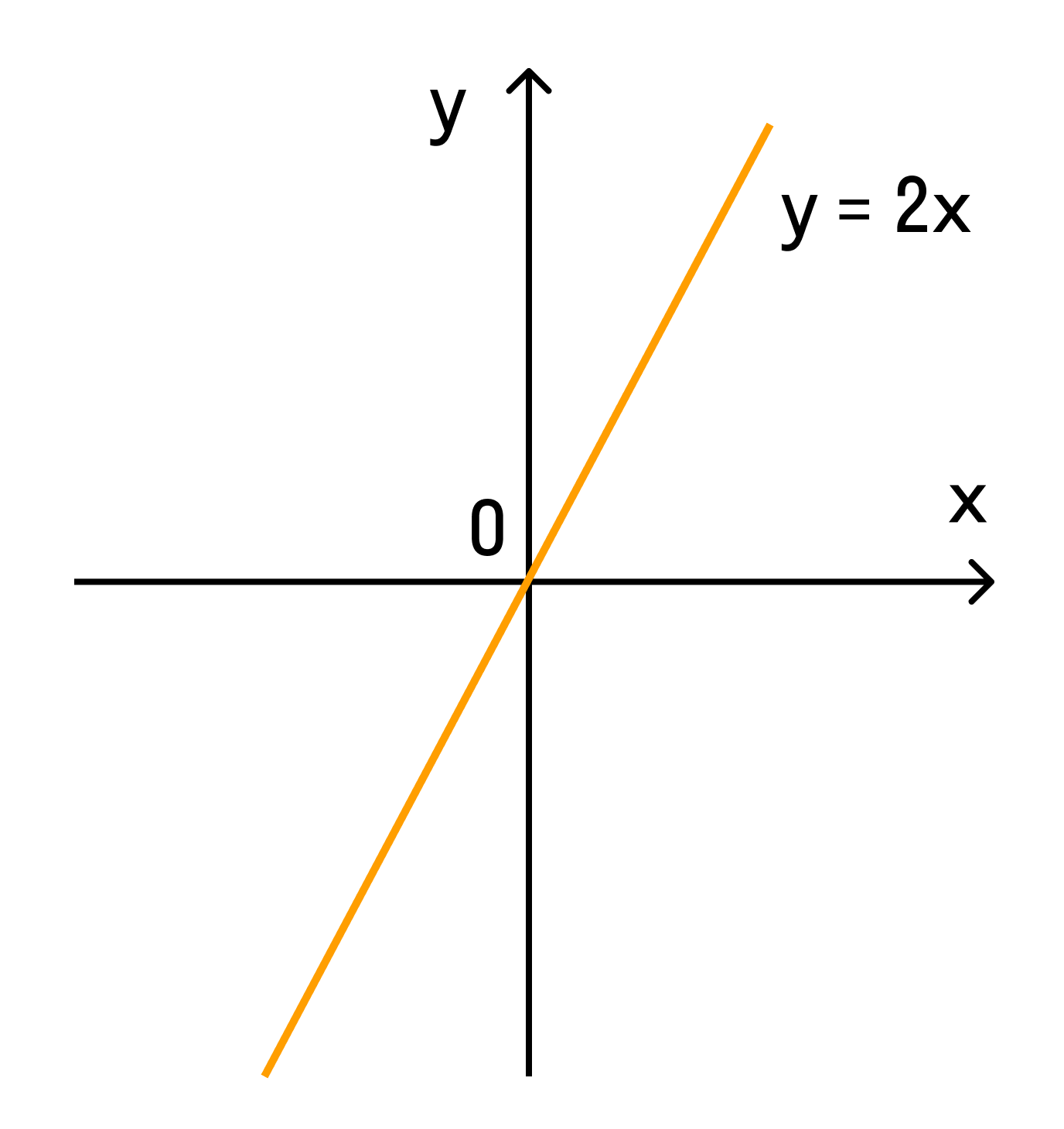Чем больше скорость тем меньше время
Время, скорость, расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 м
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 м
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Время на квантовом уровне течет иначе. Но как? И что это означает для физики?
До начала ХХ столетия считалось, что время – есть величина абсолютная. Но после того, как Альберт Эйнштейн опубликовал общую теорию относительности (ОТО), стало понятно, что время – понятие более субъективное и имеет отношение к наблюдателю, который его измеряет. И все же, многие продолжали трактовать время так, словно это прямая железнодорожная линия, двигаться по которой можно только вперед или назад. Но что, если эта железнодорожная линия ветвится или вовсе имеет окружные пути, двигаясь по которым поезд возвращается на станцию, которую уже проезжал? Иными словами, можно ли путешествовать в будущее или прошлое? Начиная со знаменитого романа Герберта Уэллса «Машина времени», научные фантасты придаются фантазиям во всю. Но в реальной жизни представить нечто подобное невозможно. Ведь если бы кто-то в будущем изобрел машину времени, неужто он бы не предупредил нас об угрозе пандемии COVID-19 или об ужасных последствиях глобального потепления? Но к нам так никто и не прибыл. Быть может, стоит посмотреть на время под другим углом?
Законы квантового мира очень сильно отличаются от тех, что мы можем непосредственно наблюдать
Квантовая механика – раздел теоретической физики, описывающий физические явления, действие в которых сравнимо по величине с постоянной Планка.
Ход времени
Наше понятие времени восходит к картине, описанной Исааком Ньютоном: стрела времени движется только вперед, лишая нас всякой возможности вернуться назад, в прошлое. В то же самое время ОТО гласит, что ход времени различен для наблюдателей в разных гравитационных полях.
Это означает, что у поверхности Земли время течет медленнее, так как сила гравитации на планете сильнее, чем на орбите. И чем сильнее гравитационное поле, тем больше этот эффект. Подробнее о том, почему время на вершине горы и на пляже течет по-разному, можно прочитать здесь.
Выходит, законы движения Ньютона положили конец идее абсолютного положения времени в пространстве, а теория относительности и вовсе поставила на этой идее крест. Более того, как пишут в своей книге «Кратчайшая история времени» физики Стивен Хокинг и Леонард Млодинов, путешествия во времени возможны.
Обложка замечательной книги Стивена Хокинга и Леонарда Млодинова, настоятельно рекомендуем к прочтению
Теория относительности показывает, что создание машины времени, способной переместить нас в будущее действительно возможно. Все, что нужно сделать после ее создания – войти внутрь, подождать некоторое время, а затем выйти – и обнаружить, что на Земле время шло иначе, нежели для вас. То есть намного быстрее. Безусловно, никто на планете не обладает подобными технологиями, но их появление – вопрос времени. Ведь если хорошенько подумать, то что нужно для изобретения такой машины?
Во-первых, она должна разгонятся до околосветовых скоростей (напомню, что скорость света достигает 300 000 км/с), а во-вторых, следует вспомнить знаменитый парадокс близнецов, при помощи которого физики пытаются доказать противоречивость специальной теории относительности, которая гласит, что с точки зрения «неподвижных» наблюдателей все процессы у двигающихся объектов замедляются.
Согласно специальной теории относительности (СТО) все физические законы одинаковы для всех свободно двигающихся наблюдателей, независимо от их скорости.
Альберт Эйнштейн опубликовал теорию относительности 106 лет назад.
Немного проясним – данный способ предполагает, что машина времени, в которую вы вошли, взлетает, разгоняется до околосветовой скорости, движется так какое-то время (в зависимости от того, как далеко вперед во времени вы направляетесь) и затем возвращается назад. Когда путешествие заканчивается, покинув машину времени вы понимаете, что для вас прошло намного меньше времени, чем для всех жителей Земли – вы совершили путешествие в будущее. Но если отныне мы воспринимаем время по-другому, быть может, законы физики подскажут, как путешествовать в прошлое?
Можно ли отправиться в прошлое?
Первый намек на то, что человек может совершать путешествия во времени, появился в 1949 году, когда австрийский математик Курт Гедель нашел новое решение уравнений Эйнштейна. Или новую структуру пространства-времени, допустимую с точки зрения ОТО.
Вообще, говоря об уравнениях Эйнштейна, важно понимать, что они удовлетворяют множество разных математических моделей Вселенной. Эти модели различаются, например, начальными или граничными условиями.
И чтобы понять, соответствуют ли они Вселенной, в которой мы живем, мы должны проверить их физические предсказания.
Кстати, если вы давно не пересматривали «Назад в будущее» – самое время)
Гедель, будучи математиком, прославился тем, что доказал – не все истинные утверждения можно доказать, даже если дело сводится к попытке доказать все истинные утверждения, например, с помощью простой арифметики. Таким образом, подобно принципу неопределенности, теорема Геделя о неполноте может быть фундаментальным ограничением нашей способности познавать и предсказывать Вселенную.
Принцип неопределенности – принцип, сформулированный Гейзенбергом и утверждающий, что нельзя одновременно точно определить и положение, и скорость частицы; чем точнее мы знаем одно, тем менее точно другое.
Интересно, что пространство-время Геделя имело любопытную особенность: Вселенная в его представлении вращалась как целое. А вот Эйнштейн был очень огорчен тем, что его уравнения допускают подобное решение. Общая теория относительности в его понимании не должна позволять путешествия во времени. Уравнение Геделя, однако, не соответствует Вселенной, в которой мы живем, но его труд позволил миру взглянуть на время (а заодно и на Вселенную) иначе.
Итак, пространство-время, как известно, тесно взаимосвязаны. Это означает, что вопрос о путешествиях во времени переплетается с проблемой перемещения на скоростях, превыщающих 300 000 км/с, то есть скорость света. А когда речь заходит о фотонах, общая теория относительности, увы, уходит на задний план, а ее место занимает квантовая механика.
Подробнее о том, что изучает квантовая механика, а главное как, мы рассказывали в этой статье, рекомендую к прочтению!
Переход на квантовый уровень
Не так давно команда физиков из Университетов Вены, Бристоля, Балеарских островов и Института квантовой оптики и квантовой информации (IQOQI-Вена) показала, как квантовые системы могут одновременно развиваться по двум противоположным временным стрелкам (вперед и назад во времени). Иными словами, квантовые системы могут двигаться как вперед, так и назад во времени.
Квантовые системы могут двигаться как вперед, так и назад во времени
Ранее, чтобы понять почему, ученые установили, что время знает только одно направление — вперед. Так что нам с вами придется вспомнить второй закон термодинамики. Он гласит, что в замкнутой системе энтропия системы (то есть мера беспорядка и случайности внутри системы) остается постоянной или увеличивается.
Если наша Вселенная представляет собой замкнутый цикл, свернутый в клубок, ее энтропия никогда не может уменьшиться, а это означает, что Вселенная никогда не вернется в более раннюю точку. Но что, если бы стрела времени «посмотрела» на явления, где изменения энтропии невелики?
Второй закон термодинамики – это статистический закон, в среднем верный для макроскопической системы. В микроскопической системе мы можем видеть, как система естественным образом эволюционируют в сторону ситуаций с более низкой энтропией, – пишут авторы научной работы.
Вот что говорит об этом Джулия Рубино, научный сотрудник Университета Бристоля и ведущий автор новой статьи: «Давайте предположим, что в начале газ в сосуде занимает только его половину. Затем представьте, что мы удаляем клапан, который удерживал его в пределах половины сосуда, так что газ теперь может свободно расширяться по всему сосуду».
Термодинамика хранит в себе множество тайн о нашем мире и Вселенной
В результате мы увидим, что частицы начнут свободно перемещаться по всему объему сосуда. Со временем газ займет весь сосуд. «В принципе, существует ненулевая вероятность того, что в какой-то момент газ естественным образом вернется, чтобы занять половину сосуда, только эта вероятность становится меньше, чем больше становится количество частиц, составляющих газ», – объясняет Рубино.
Если бы существовало только три частицы газа вместо огромного количества газа (состоящего из миллиардов частиц), эти несколько частиц могли бы снова оказаться в той части сосуда, откуда они первоначально стартовали. Вот такая физика.
ОТО допускает путешествия во времени в будущее. С прошлым все намного сложнее
Далее, как вы могли догадаться, следует второй закон термодинамики – так называемый статистический закон, который является верным в среднем для макроскопической системы. «В микроскопической системе мы можем видеть, как система естественным образом эволюционирует в сторону ситуаций с более низкой энтропией», – отмечают исследователи.
Стрела времени
Чтобы разобраться еще подробнее, отметим, что в ходе нового исследования физики задавались вопросом о последствиях применения описанной выше парадигмы в квантовой области. Согласно принципу квантовой суперпозиции, отдельные единицы (например, свет) могут существовать одновременно в двух состояниях, как в виде волн, так и в виде частиц, проявляясь в том или ином виде в зависимости от того, что именно вы тестируете.
Команда Рубино рассмотрела квантовую суперпозицию с состоянием, которое развивается как назад, так и вперед во времени. Измерения показали, что чаще всего система в конечном итоге движется вперед во времени. Если бы не небольшие изменения энтропии, система действительно могла бы продолжать развиваться как вперед, так и назад во времени.
Разрушение суперпозиции состоянии при взаимодействии с окружением с течением времени Изображение Joint Quantum Institute
Так как же эти сложные физические понятия соотносятся с реальным человеческим опытом? Неужели наконец-то пришло время начать собирать вещи для путешествия назад во времени? Увы.
«Мы, люди, являемся макроскопическими системами. Мы не можем воспринимать эти квантовые суперпозиции временных эволюций», – говорит Рубино. Для нас время действительно движется вперед. Возможно, это тот случай, когда мир немного не определился.
И действительно – на самом фундаментальном уровне мир состоит из квантовых систем (которые могут двигаться вперед и назад). Более глубокое понимание того, как описать течение времени на уровне этих элементарных составляющих, могло бы позволить физикам сформулировать более точные теории для их описания и, в конечном счете, получить более глубокое понимание физических явлений мира, в котором мы живем.
Еще больше интересных статей обо всем на свете, а также о путешествиях во времени и Мультивселенной читайте на нашем канале в Яндекс.Дзен. Там регулярно выходят статьи, которых нет на сайте!
Выводы
Однако не все согласны с тем, что различие между макроскопическим и микроскопическим является четким. Как пишет Popular Mechanics, Рамакришна Подила, доцент кафедры физики и астрономии Университета Клемсона в Южной Каролине, говорит, что статистика многих частиц по сравнению со статистикой отдельных частиц является более точным способом описания вещей.
Даже у одной частицы есть свои собственные, уникальные микросостояния. Подила считает, что в нашем стремлении понять время мы ставим уравнения выше физической реальности — и упускаем главное.
Связывание стрелы времени с энтропией или коллапсом квантово-механической системы (как указано в статье) – это не формальные утверждения, а популярные методы, которые просты в использовании. Даже то, что время движется вперед, само по себе не аксиома, а теория, которую астрофизик Артур Эддингтон придумал и популяризировал в 1927 году.
Время и пространство неразрывно связаны, но правильно ли мы их понимаем?
Так что, возможно, идея о том, что пространство и время сливаются в один переплетенный континуум, имеет право на жизнь. С тех пор как Альберт Эйнштейн сформулировал теорию относительности, мы перестали воспринимать пространство как трехмерную фигуру, а время — как одномерное.
Время стало четвертым элементом четырехмерного вектора, описывающего пространство и время, — говорит Рубино. Это единая, динамичная сущность, над которой мы все еще ломаем голову.
В заключение же хочу не только поблагодарить читателя за внимание, но и вновь процитировать ученых: «Хотя время часто рассматривается как непрерывно увеличивающийся параметр, наше исследование показывает, что законы, управляющие его течением в квантово-механических контекстах, намного сложнее. Это может означать, что нам нужно переосмыслить то, как мы представляем эту величину во всех тех контекстах, где квантовые законы играют решающую роль».
Из-за квантовой суперпозиции ход времени в микромире не имеет определенного направления — исчезает грань между причиной и следствием.
Полностью ознакомиться с текстом научной работы можно в журнале Nature. Кстати, как вы думаете, можно ли путешествовать во времени и что новое исследование говорит нам о Вселенной? Ответ будем ждать здесь, а также в комментариях к этой статье!
Новости, статьи и анонсы публикаций
Свободное общение и обсуждение материалов
Итак, ученые обнаружили гравитационные волны — рябь пространства-времени. Альберт Эйнштейн предположил их существование еще 100 лет назад, и прямые наблюдени…
Может ли Вселенная поглотить сама себя изнутри? К счастью для нас, физики, изучающие явление, называемое “распадом пространства-времени”, считают это маловер…
На протяжении веков человечество вгрызалось в гранит науки, пытаясь выяснить точный состав Вселенной. Древние греки первыми предположили существование атомов…
Прямая и обратная пропорциональность
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Зависимости также можно классифицировать по формам: функциональная и статистическая.
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.
В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.
Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.
Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
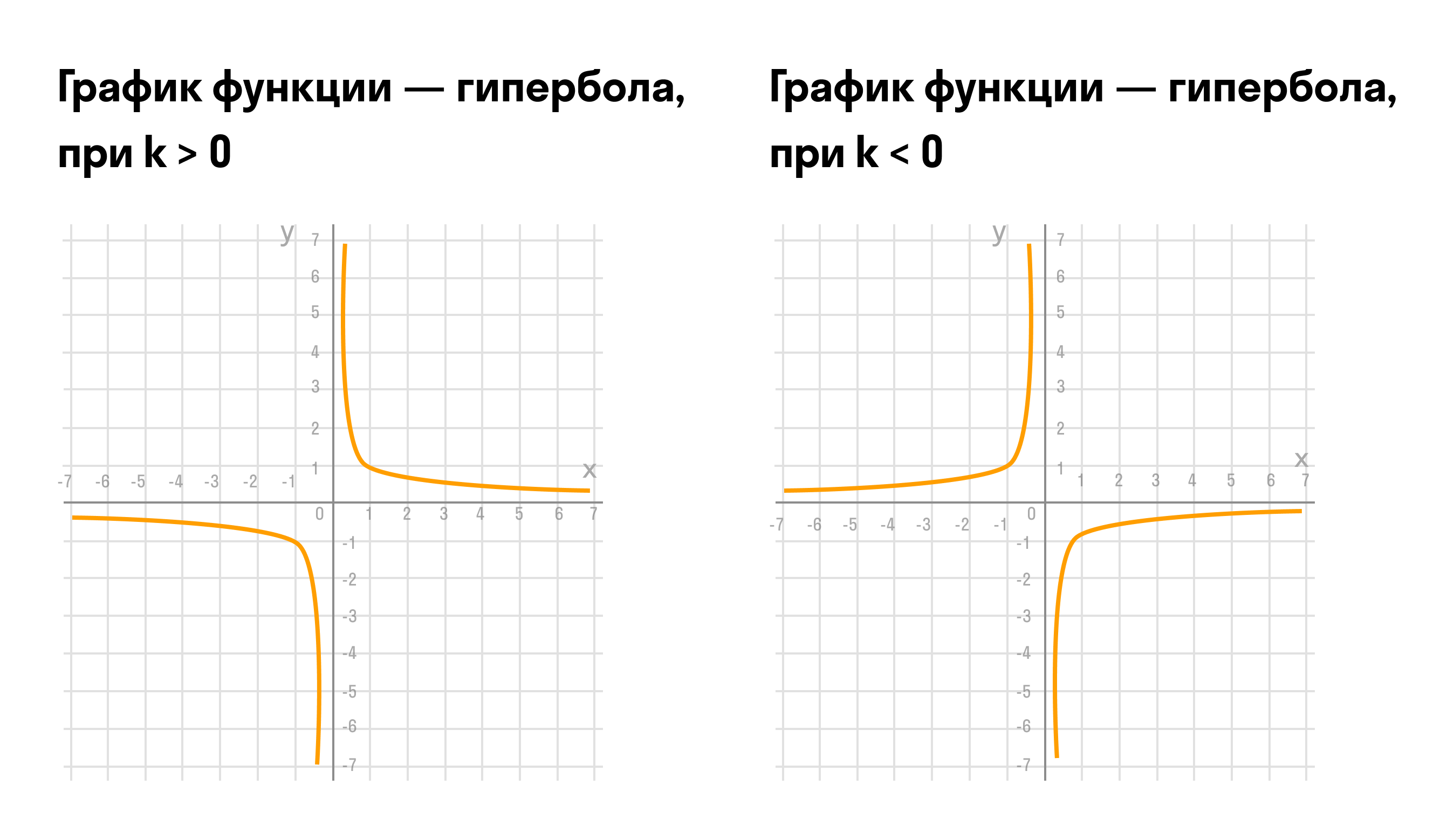
Графиком обратно пропорциональной зависимости величин является гипербола.
Свойства функции обратной пропорциональности:
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.