Чем больше сыра тем меньше сыра
Забавные парадоксы, которые ставят в тупик
1. Парадокс Крокодила
2. Парадокс Пиноккио
Мы все знаем, что нос Пиноккио растёт, когда он врёт. Что произойдет, если Пиноккио скажет «сейчас мой нос удлинится»? Ведь если нос действительно удлинится, то получается, что Пиноккио сказал правду, а от правды нос не должен расти. А если нос не удлинится, то выходит что Пиноккио соврал — и это должно было привести к росту его носа.
3. Корабль Тесея
Корабль Тесея — парадокс, который можно сформулировать так: «Если все составные части исходного объекта были заменены, остаётся ли объект тем же объектом?»
Объясняем. Допустим у нас есть корабль сделанный из дерева. Назовём его кораблём Тесея. Со временем судно начинает гнить, и вы меняете доски одну за другой на такие же, только новые, пока не остаётся ни одной исходной доски. А теперь вопрос: Является ли этот корабль тем же кораблём Тесея, или это уже другой корабль?
4. Парадокс ума
Чем больше вы узнаете, тем больше понимаете, как мало вы знаете. Старая пословица Сократа. Каждый раз, когда вы начинаете лучше понимать, это создает даже больше вопросов, чем ответов. Получается, что чем вы умнее, тем глупее себя ощущаете.
Хороший повод, чтобы не делать в следующий раз домашнюю работу 🙂
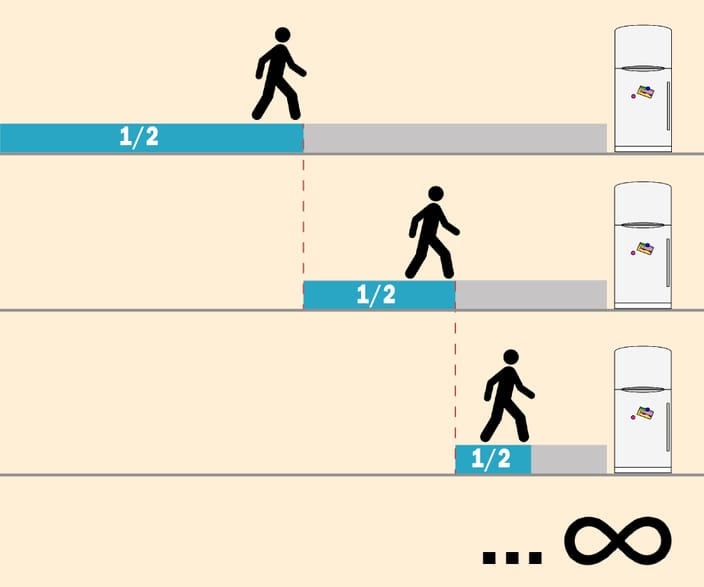
5. Парадокс половины
Представьте, что вам нужно дойти до холодильника. Чтобы преодолеть весь путь до холодильника, нужно сначала преодолеть половину пути, после этого половину из оставшегося пути, а потом половину из этой половины, и так далее до бесконечности. Из этого вывод, что вы постепенно будете приближаться к холодильнику, но никогда его не достигнете. Получается, что мы никогда не дойдём до холодильника, но всё равно толстеем 🙁
Следующий раз, когда мама отругает вас за то, что вы не помыли посуду, скажите ей что вы просто не смогли дойти до посуды.
6. Парадокс стрелы
Парадокс стрелы, или стрела Зенона, является парадоксом, который показывает, что любое движение невозможно. Другими словами — движения не существует.
Парадокс заключается в следующем: если зацепить свой взгляд в определенный момент времени на летящей стреле, то она представится неподвижной. И в каждый момент времени стрела будет неподвижной. Если не существует момента, когда стрела движется, то из этого следует, что она неподвижна. Вопреки видимому, стрела в полёте не может двигаться.
Другими словами, вы видите, что стрела двигается в полёте, но согласно сказанному выше, она не должна двигаться.
И напоследок забавный парадокс сыра
Больше сыра — больше дырок, больше дырок — меньше сыра, получается что чем больше сыра — тем меньше сыра?
Получается что все утверждения исходят друг от друга, но последняя сильно противоречит самой себе. Чем больше кусок сыра — тем больше количество дырок в нём. Но чем больше в нём дырок, значит тем больше в сыре пустого пространства, и сыра меньше. Так выходит, что чем больше кусок сыра, тем меньше в нем сыра?
Чем больше сыра тем меньше сыра
увеличение объёма сыра не пропорционально увеличению объёма дырок..так как скажем в 1кг сыра- сыра больше чем дырок иначе не было бы сыра значит при увеличении объёма-мы получим сыра больше чем дырок. чем больше сыра-тем больше дырок, но тем больше сыра)))
ну короче, больше тренируешься-больше устаешь, больше устаешь-меньше тренируешься, больше тренируешься-меньше тренируешься. Ты меня не учи софизму, я собаку сожрал в этом деле
у собаки вкусное мясо, советую попробовать
По сути, чем больше сыра (с дырками), тем меньше объема сыра без дырок. Потому что с увеличением кол-ва сыра, увеличивается и кол-во дырок.
ЯБывают сыры без дырок) Это раз. А дав—сыр продают на вес—а не на «объём» так что от будь он хоть бубликом—его меньше не станет)
А в хлебе видел сколько дырок. Значит чем больше мы едим бутербродов. тем едим меньше.
Всё зависит от конкретного количества дырок на конкретный сантиметр площади сыра.
чем больше сыра тем меньше дырок) выбираете плавленный сыр. там вообще нет дырок))
Чем больше сыра, тем сытнее обед, а дырки пофиг, они не такого размера, как сыр)
Ни фига се. С утра и такой вопрос получить. голову можно сломать. )))))))))))
дырок в сыре много не бывает!))))) или покупайте тогда сыр без дырок!)))))
у каждого своя суть,бери сыр без дырок и заморачиваться не придётся
Чем меньше сыра тем меньше дырок, чем меньше дырок тем больше сыра)))
Чем лучше сыр, тем больше дыры (их не много, они большие должны быть)
А суть проста,чем больше сыра тем меньше народу достанется.
Самые интересные логические парадоксы
Парадокс означает некое утверждение, которое отличается от общепринятого. Или это явление, существование которого кажется невозможным и весьма неожиданным. В качестве одного из примеров можно привести парадоксальное рассуждение Алисы из сказки, написанной Льюисом Кэроллом. Алиса размышляла: «Чем больше сыра, тем больше в нем дырок, но ведь, чем больше дырок, тем меньше остается сыра. Соответственно, чем больше сыра, тем меньше его будет?» Многие специалисты начали пытаться разбирать самые интересные логические парадоксы. Давайте рассмотрим наиболее яркие примеры.
Проклятая бутылка Стивенсона
Еще одна сказка, написанная Робертом Льюисом Стивенсоном, под названием «Сатанинская бутылка», знакомит читателя со спокойным гавайцем Кэаве, который приобретает бутылку с чертом, исполняющим абсолютно любые желания. Взамен этого владелец бутылки после смерти должен попасть в ад, если только ему не удастся продать эту бутылку дешевле, чем он приобрел ее сам. Парадокс здесь заключается в том, что, запросив за нее, например, 50 рублей, продать ее можно в принципе кому угодно. Но главным условием черта было совершение честного договора, то есть новый покупатель должен будет знать о таких последствиях. По словам автора, такая книга ранее стоила огромных денег, а владел ей даже сам Наполеон. То есть, даже если попытаться приобрести ее за максимальную сумму, то средств может просто напросто не хватить, да и найти покупателя будет крайне сложно, ведь чем больше сумма, тем меньше ценность такой бутылки.
Автор данной сказки решил эту задачу довольно простым образом. Выбор решения состоял из трех опций: сделка с использованием курса валюты других стран, самопожертвование (допустим, близкий родственник или любимый человек решается приобрести данную бутылку, чтобы снять проклятие), и последнее — алчный покупатель с безразличием к жизни после смерти. Несмотря на это, данная задача и по сей день считается одним из самых интересных логических парадоксов.
Известный с античных времен логический парадокс лжеца
Еще с древних времен известно суждение: «Данное высказывание — ложно. Истинно ли это или нет?». Любой скажет, что здесь ответ может быть как положительным, так и отрицательным. По этому поводу высказывал свои мысли популярный научный деятель начала двадцатого века Бертран Рассел. Он говорил, что эта загадка, которая в древности воспринималась как шутка, имеет отношение к кардинальным и ординальным числам. Парадокс лжеца — не единственное, над чем работал Рассел. Его главное достижение — опровержение наивной теории множеств Кантора.
Образование новых штатов
Число представителей от старых штатов может изменяться с появлением еще одного штата. Этот парадокс был обнаружен еще в начале двадцатого века во времена, когда Оклахома отделилась и стала самостоятельной. Прежде Палата представителей состояла из 386 мест. В соответствии с населением Оклахомы было решено выделить для данного штата 5 мест. Исходя из этого, общее число мест Палаты стало 391. Однако при этом предполагалось, что число мест других штатов останется прежним. Но в результате пропорционально-территориального распределения мест штат Мэн получил дополнительное представительское место, а Нью-Йорк, в свою очередь одного места лишился.
Парадокс бережливости
Многие знают изречение Брежнева о том, что экономика должна быть экономной. Но не всегда экономия приносит пользу. Если все люди вместе станут экономить в период кризиса, то это приведет к снижению спроса товаров, после чего последует разорение фирм и, соответственно, снижение зарплат в совокупности с ростом безработицы. Таким образом, формируется некий якорь, который как бы «тащит» экономику вниз. Однако существует и иное мнение. В классической модели экономики подразумевается, что чем больше доходов идет на сбережение, тем значительней становятся темпы роста экономики в целом.
Парадокс воронов
Карл Густав Гемпель — это философ, который интересно объясняет данный парадокс. Предположим, что каждый ворон черного цвета. Следуя простой логике, все не являющиеся чёрными предметы не будут считаться воронами. Чем больше человек увидит черных воронов, тем сильнее закрепится в его сознании, что все вороны одинакового цвета. Увидев же коричневых коров, белых медведей и синие ели человек только усилит свое мнение о том, что все не являющиеся чёрными предметы — это не вороны. Но подобный вывод в корне противоречит интуитивному восприятию реальности. Если же человек натолкнется на белого медведя, в большей вероятности, это увеличит уверенность в том, что все не являющиеся чёрными предметы не будут считаться воронами, но при этом вряд ли это заставит его думать, что все вороны обязательно должны быть черного цвета.
Лотерейный парадокс
Вероятность выигрыша конкретного лотерейного билета в отдельности очень мала. Невозможно знать заранее, какой билет выигрышный, но мы точно знаем, что один из билетов является таковым. Таким образом, мы можем считать, что выигрышный билет среди огромного числа билетов, скорее всего, не первый, вряд ли второй и так далее, вплоть до последнего. Тем самым, мы считаем, что каждый билет не является выигрышным, однако понимаем, что один из них точно таковым является.
Парадокс всемогущества
Суть этого парадокса связана со следующим вопросом: способен ли Всемогущий создать камень, который он был бы не в силах поднять? То есть, если Всемогущий может создать такой камень, но не может его поднять, то его могущество становится спорным. А если же он не может создать такой камень, то опять же его всемогущество ставится под вопрос. Отвечая на этот вопрос, некоторые философы утверждали, что Бог не может создать ситуацию, при которой он подверг бы сомнению свое могущество. А другие утверждали, что существование Всемогущего не может быть воспринято человеческим разумом и находится вне человеческой логики.
Почему важно развивать логическое мышление?
Развитая логика — это возможность правильно анализировать различные ситуации и принимать верные решения. Применение логики в жизни позволяет быстро распознавать обман, эффективно работать с большими объемами информации, решать массу сложных задач. Всё это говорит о том, что работа над логическим мышлением необходима человеку. У Викиум есть специальный курс для этого — «Мышление Шерлока». Кроме того, на сайте можно найти много интересных и полезных тренажеров, также направленных на развитие логики. Умение мыслить логически не дается просто так, этому нужно учиться. Поэтому советуем не терять время!
10 занятных парадоксов для любителей поломать голову
Парадоксом называют такую ситуацию или утверждение, которое разбивает привычное представление об истине и на первый взгляд противоречит здравому смыслу. Сочинением парадоксов занимались самые выдающиеся мудрецы
Парадоксом называют такую ситуацию или утверждение, которое разбивает привычное представление об истине и на первый взгляд противоречит здравому смыслу. Сочинением парадоксов занимались самые выдающиеся мудрецы. Вот несколько ярких примеров:
Парадокс-сорит
Если из горсти песка убрать одну песчинку, то она всё равно останется горстью песка. Продолжайте убирать песчинку за песчинкой и в какой-то момент горсть исчезнет. Может ли одна единственная песчинка определять разницу между горстью песка и ее отсутствием?
Парадокс Пиноккио
Этот итальянский парень, как известно, был деревянным врунишкой. Кроме того, у него было одно уникальное свойство: как только он говорил неправду, его нос немного подрастал. И тут обнаруживается любопытный парадокс:
Что будет, если он скажет: «Сейчас у меня вырастет нос»?
Если нос не вырастет — получится, что парень соврал, и носу полагается вырасти. А если нос вырастет — значит, он сказал правду, тогда с чего бы носу расти?
Девочка и её бабушка
Парадокс швейцарского сыра
В швейцарском сыре много дырок. Чем больше дырок – тем меньше сыра. Чем больше сыра – тем больше дырок. Получается, чем больше сыра – тем меньше сыра.
Да или нет?
Попробуйте ответить правдиво (либо “да”, либо “нет”) на следующий вопрос: “Будет ли следующее слово, которое вы произнесёте, словом “нет”?
Парадокс пирата
Всё детство мне внушали, что надо делиться, а теперь они арестовали меня именно за это!
Парадокс хипстера
Хипстеры – это люди, которые стараются быть “не как все”. Однако если они оказываются невероятно популярными и большинство людей становится хипстерами, то хипстеры оказываются мейнстримом и перестают быть хипстерами.
Парадокс миссионера
Один миссионер попал в плен к людоедам и те задумали устроить праздничный обед. Миссионер слёзно просит его отпустить, но людоеды соглашаются всего-навсего предоставить несчастному самому определить, будет он зажарен или сварен. Для этого ему предлагают произнести какое-нибудь высказывание с условием, что, если это высказывание окажется истинным, они его сварят, а если оно окажется ложным, его зажарят.
Парадокс обнаруживается, когда сообразительный миссионер отвечает: «Вы меня зажарите». Людоеды оказываются в безвыходной ситуации: если они действительно зажарят миссионера, то получится, что его слова истинны, стало быть, его следовало сварить. Если же его сварят, его высказывание окажется ложным, и его следовало зажарить.
Парадокс всемогущества
«Допустим, существует некто, в чьих силах абсолютно все. По идее, это существо должно быть в состоянии придумать задачу, которую не сможет выполнить; таким образом, это существо не может выполнить любую задачу. С другой стороны, если это существо не может придумать для себя невыполнимую задачу, значит, существует все же что-то, что оно не может сделать».
Парадокс “Корабль Тесея”
«Вполне логичным выглядит утверждение, что можно заменить любую часть корпуса или оснастки корабля, и при этом корабль останется тем же кораблем Тесея. Тогда можно заменить все составные части корабля постепенно, одну за другой, на новые, и все равно это будет тот же корабль. А если из всех оригинальных частей корабля, в свое время замененных на новые, собрать целый корабль, которое из двух получившихся судов будет тем же кораблем Тесея?» опубликовано econet.ru
Понравилась статья? Напишите свое мнение в комментариях.
Подпишитесь на наш ФБ:
Чем больше сыра тем меньше сыра
Чем больше сыра, тем больше в нём дырок, но, чем больше дырок, тем меньше сыра. Получается, чем больше сыра, тем меньше сыра? сыр дырка
В таком абстрактном понятии можно прийти и к такому выводу. Просто это как сравнивать одинаковые числа, но в разных системах исчисления.
Ната иногда полезно что в хлебе ну очень много дырок!)) еще много дырок на чулках в сеточку..ну очень много. далее по твоей формуле!)))
Чем больше сыр,тем больше дырок в нем,все пряиопропорционально друг другу или по другому количество зависит от обьема!!)))))))))))
Это может стать началом неплохой сырно–финансовой пирамиды. Только убедить всех, что мало это много.
если хороший сыр не бывает без дырок,значит дырки это сыр, получается чем больше дырок тем больше сыра
Если в сыре много дыр, значит вкусным будет сыр. Если в нем одна дыра,значит вкусным был вчера!