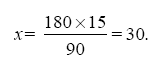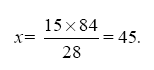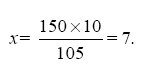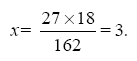Чем длиннее рычаг тем меньше
Почему, чем больше рычаг, тем меньше тратится сил

Добрый день. Подскажите есть ли средство для рейтингования таким образом чтобы меньшее значение.
«Чем больше женщину мы любим, тем меньше нравимся мы ей»
Я привел известную цитату Пушкина. Что вы думаете по этому поводу? Я пока не определился.
Чем меньше интервал таймера, тем больше он «врет»
Ситуация в следующем. Пытаюсь разобраться с таймером в C#. Написав некоторый код программы и.
Добавлено через 20 минут
Он может быть объяснён на основе более общих законов (наподобие уравнений статики для моментов силы и закона сохранения энергии для них же), и в некоторых специфических условиях для очень маленьких (атомные ядра) или очень быстрых (около скоростей света) он не выполняется, но в быту его нарушение может представиться в случае обманщиков (из оперы «обвеса» полыми гирями на рычажных весах и т.д.), а так он всегда выполняется.
Добавлено через 5 минут
Мда. Не шибко в мультике объяснили. Не шибко)
Добавлено через 2 часа 34 минуты

Нужно написать программу, которая каждую мс будет выполнять определенное действие. За основу решил.
Чем больше тем лучше ЧБТЛ спасибо
Прошел курс само учителя на Яве хочу отточить свои знания задайте пож для меня какие нибудь задания.
Рычаги
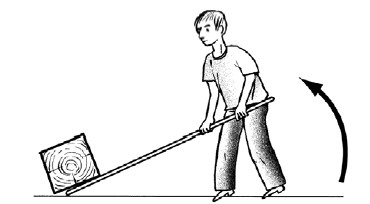
Когда приходится приподнимать тяжелый груз, например, большой валун на поле, часто поступают так: подсовывают прочную палку одним концом под валун, подкладывают близ этого конца небольшой камень, полено или что-нибудь другое для опоры и налегают рукой на другой конец палки. Если валун слишком тяжел, то таким способом удается его приподнять с места.
Такая прочная палка, могущая поворачиваться вокруг одной точки, называется «рычагом», а точка, вокруг которой рычаг поворачивается, – его «точкой опоры». Надо запомнить также, что расстояние от руки (вообще от точки, где приложена сила) до точки опоры называется «плечом рычага»; так же называется расстояние от места, где на рычаг напирает камень, до точки опоры. У каждого рычага, следовательно, два плеча. Эти названия частей рычага нам нужны для того, чтобы было удобнее описать его действие.
Испытать работу рычага нетрудно: вы можете превратить в рычаг любую палочку и пробовать опрокидывать ею хотя бы стопку книг, подпирая свой рычаг книгой же. При таких опытах вы заметите, что, чем длиннее плечо, на которое вы напираете рукой, по сравнению с другим плечом, тем легче поднять груз. Вы можете на рычаге небольшою силою уравновесить большой груз только тогда, когда действуете на достаточно длинное плечо рычага, – длинное по сравнению с другим плечом. Каково же должно быть соотношение между вашею силою, величиной груза и плечами рычага, чтобы сила ваша уравновешивала груз? Соотношение таково: ваша сила должна быть во столько раз меньше груза, во сколько раз короткое плечо меньше длинного.
Приведем пример. Предположим, нужно поднять камень весом 180 кг; короткое плечо рычага равно 15 см, а длинное – 90 см. Силу, с которой вы должны напирать на конец рычага, обозначим буквой х. Тогда должна существовать пропорция:
Значит, вы должны напирать на длинное плечо с силою 30 кг.
Еще пример: вы в состоянии налегать на конец длинного плеча рычага с силою только 15 кг. Какой наибольший груз можете вы поднять, если длинное плечо равно 64 см, а короткое – 28 см?
Обозначив неизвестный груз через х, составляем пропорцию:
Значит, вы можете таким рычагом поднять не больше 45 кг.
Сходным образом можно вычислить и длину плеча рычага, если она неизвестна. Например, сила в 10 кг уравновешивает на рычаге груз в 150 кг. Какой длины короткое плечо этого рычага, если его длинное плечо равно 105 см?
Обозначив длину короткого плеча буквою х, составляем пропорцию:
Короткое плечо равно 7 см.
Тот вид рычага, который был рассмотрен, называется рычагом первого рода. Существует еще рычаг второго рода, с которым мы теперь познакомимся.
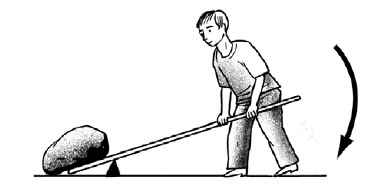
Предположим, нужно поднять большой брус (рис. 14). Если он слишком тяжел для ваших сил, то вы засовываете под брус прочную палку, упираете ее конец в пол и тянете за другой конец вверх. В данном случае палка является рычагом; точка его опоры на самом конце; ваша сила действует на второй конец; но груз напирает на рычаг не по другую сторону от точки опоры, а по ту же сторону, где приложена ваша сила. Иными словами, плечи рычага в данном случае: длинное – полная длина рычага и короткое – часть его, засунутая под брус. Точка же опоры лежит не между силами, а вне их. В этом отличие рычага 2-го рода от рычага 1-го рода, у которого груз и сила расположены по разные стороны от точки опоры.
Рис. 14. Рычаги 1-го и 2-го рода: груз и сила расположены по разные стороны от точки опоры
Несмотря на это отличие, соотношение сил и плеч на рычаге 2-го рода такое же, как на рычаге 1-го рода: сила и груз обратно пропорциональны длинам плеч[4]. В нашем случае, если для непосредственного поднятия двери нужно, например, 27 кг, а длина плеч 18 см и 162 см, то сила х, с которой вы должны действовать на конец рычага, определяется из пропорции
Ваше усилие должно быть не меньше 3 кг (не меньше потому, что сила в 3 кг только уравновешивает сопротивление двери).
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
11. Сочленения и рычаги в опорно-двигательном аппарате человека. Эргометрия
11. Сочленения и рычаги в опорно-двигательном аппарате человека. Эргометрия Движущиеся части механизмов обычно бывают соединены частями. Подвижное соединение нескольких звеньев образует кинематическую связь. Тело человека – пример кинематической связи.
Чем длиннее рычаг тем меньше
1. Что такое рычаг?
Самый простой и распространенный механизм — рычаг.
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.
2. Как используют рычаг?
Можно для поднятия груза использовать в качестве рычага лом.
Для этого надо с силой F нажимать на конец лома В или приподнимать конец В.
В любом случае при поднятии груза необходимо преодолеть вес груза Р — силу, направленную вертикально вниз.
Для этого надо повернуть лом вокруг оси, проходящей через неподвижную точку лома — точку его опоры О.
Сила F, с которой человек действует на рычаг, меньше силы Р.
Используя рычаг, получаем выигрыш в силе.
2. Что называют плечом силы?
Например, есть рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В.
F1 и F2, действующие на рычаг, направлены в одну сторону.
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
3. Как найти плечо силы?
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Длина этого перпендикуляра и будет плечом данной силы.
OA — плечо силы F1,
OB — плечо силы F2.
4. Какое действие оказывают на рычаг силы?
Силы, действующие на рычаг, могут повернуть его вокруг оси или по ходу, или против хода часовой стрелки.
На рисунке выше:
С ила F2 вращает рычаг по ходу часовой стрелки.
Сила F1 вращает рычаг против хода часовой стрелки.
Результат действия силы зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу и как направлена.
5. В чем состоит правило (условие) равновесия рычага?
Правило равновесия рычага было установлено Архимедом (287—212 гг. до н. э.).
Правило (условие) равновесия рычага:
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
К рычагу по обе стороны от точки опоры подвешивают грузы так, чтобы рычаг оставался в равновесии.
Действующие на рычаг силы равны весам этих грузов.
Далее измеряют модули сил и их плечи.
Если сила F2 уравновешивает силу F1, то плечо меньшей силы в 2 раза больше плеча большей силы.
где
F1 и F2 — силы, действующие на рычаг,
l1 и l2 — плечи этих сил.
6. Как уравновесить меньшей силой большую?
При помощи рычага можно меньшей силой уравновесить большую силу.
При этом плечо меньшей силы должно быть длиннее плеча большей силы.
Задача.
Человеку необходимо поднять с помощью рычага плиту массой 240 кг.
Большее плечо рычага равно 2,4 м.
Меньшее плечо рычага равно 0,6 м.
Какую силу надо приложить человеку к большему плечу рычага?

Человек преодолевает силу 2400 Н, прикладывая свою силу, равную 600 Н.
Здесь рычаг дает выигрыш в силе в 4 раза.
Однако плечо, на которое действует человек, в 4 раза длиннее того, на которое действует вес плиты:
2,4 м : 0,6 м = 4.
Что это рычаг в физике? Принцип работы рычага. Виды рычагов
Физическое понятие о рычаге

На рисунке выше показан рассмотренный простой механизм, который является рычагом первого рода (см. ниже).
Историческая справка
Каждый школьник слышал уже в 7 классе о знаменитом рычаге Архимеда. Греческий философ утверждал, что при определенных размерах этого простого механизма он мог бы перевернуть нашу Землю, будь вторая такая планета, которую можно было бы использовать в качестве опоры. Архимеду действительно принадлежит большая заслуга в развитии статики, поскольку он смог экспериментально получить математическое равенство, которое в настоящее время носит название «Условия равновесия рычага».
Однако сам принцип рычага использовался задолго до нашей эры. Так, известно, что для забора воды из рек применялся этот простой механизм. Существуют исторические свидетельства, что при строительстве пирамид египтяне также применяли систему рычагов.
Принцип работы рычага
Познакомившись с вопросом, что такое рычаг в физике (это наипростейший механизм), перейдем к рассмотрению принципа, согласно которому с помощью рычага получается выигрыш в силе или в пути перемещения. Для этого вспомним, что в физике существует величина, которая называется моментом силы. Последний равен произведению плеча силы на модуль силы, то есть:
Если вспомнить статику, то второе условие равновесия системы твердых тел в ней гласит, что система не будет совершать вращательного движения, если сумма всех n моментов сил в ней равна нулевому значению. То есть:
Прежде чем переходить к формулировке условия равновесия рычага, отметим, что момент силы, который стремится повернуть систему против часовой стрелки, является положительным. Противоположный ему момент будет отрицательным.
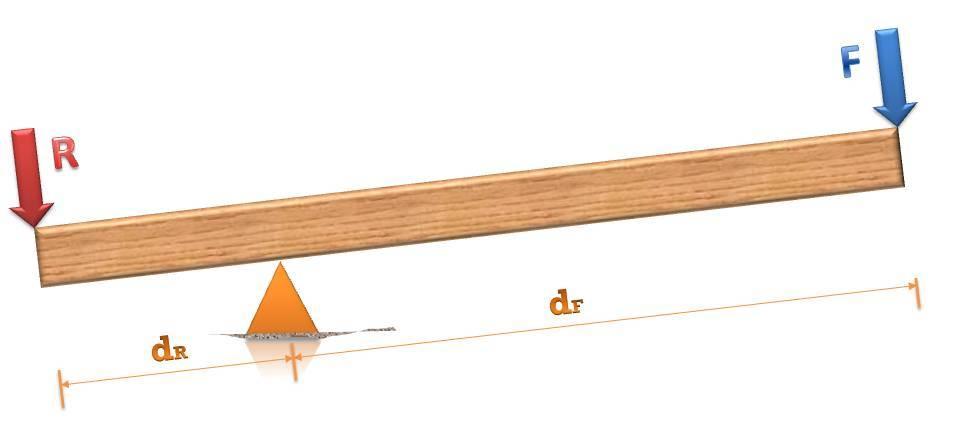
Выше показан рычаг, на который оказывают действие внешняя сила F и сила нагрузки R. Учитывая значение плеч сил и направления моментов, можно записать следующее равенство:
Откуда получаем условие равновесия рычага, полученное еще Архимедом:
Это условие говорит о том, что чем длиннее плечо dF, тем меньшую силу F следует приложить, чтобы поднять вес R. При этом высота подъема этого веса будет меньше, чем высота, на которую опустится плечо dF. Таким образом, при dF>dR получается выигрыш в силе, но проигрыш в пути. При обратном соотношении плеч получится выигрыш уже в пути, но силу F придется приложить большей величины, чем вес R.
Таким образом рычаг можно применять как для подъема тяжестей, так и для сообщения скорости телу весом R. Последнее раньше использовалось в катапультах.
Виды рычагов и примеры
В зависимости от положения опоры и порядка расположения действующих на балку сил рычаги бывают трех родов. Расскажем кратко об особенностях каждого из них.
В качестве рычагов третьего рода можно привести в пример рыбацкую удочку, пинцет или столовую вилку.
Простые механизмы. «Золотое правило» механики
п.1. Виды простых механизмов
По традиции, сложившейся ещё со времен Возрождения, к простым механизмам относятся:
Примеры физических систем в механике
п.2. Принцип действия рычага
Подробно рычаги и условия равновесия были рассмотрены в §26 данного справочника.
В этом разделе мы рассмотрим принцип работы рычага с точки зрения закона сохранения энергии.
Пусть действие приложенной силы \(F_1\) приводит к перемещению \(h_1\) левого плеча вниз.
Работа приложенной силы равна \(A_1=F_1h_1\).
Тогда правое плечо при этом переместится вверх на расстояние \(h_2\).
Получаем, что \(F_1h_1=F_2h_2\).
Что соответствует результату, полученному ранее.
п.3. «Золотое правило» механики
 | Архимеду приписывают следующую фразу: «Дайте мне точку опоры, и я переверну Землю». |
Попробуем для начала хотя бы сдвинуть Землю на 1 микрон с орбиты, \(h_2=1\ \text<мкм>=10^<-6>\ \text<м>\). Это послужит хорошей иллюстрацией «золотого ПРАВИЛО» механики.
Расстояние от Солнца до Земли – 1 астрономическая единица – это «всего лишь» 150 миллионов километров:\(1\ \text<а.е.>\approx 1,5\cdot 10^<11>\ \text<(м)>\).
Значит, если на одной стороне рычага мы сдвигаем Землю на 1 микрон, то на другой стороне – прикладывая весь свой вес – должны преодолеть расстояние в полторы Солнечных системы. Вот что такое – «проигрыш в расстоянии».
п.4. Блоки и полиспасты
Блок — это колесо с желобом, по которому пропущена веревка или трос.
В технике используют неподвижные и подвижные блоки.
Подвижный блок даёт выигрыш в силе в 2 раза.
При этом получаем двойной проигрыш в расстоянии: чтобы поднять груз на высоту \(h\), нужно вытравить канат справа на длину \(2h\).
В реальных ситуациях выигрыш в силе при использовании подвижного блока получается меньшим, т.к. часть работы уходит на подъем самой веревки и блока (они тоже имеют вес) и преодоление трения.
На практике используют комбинации из неподвижных и подвижных блоков – полиспасты.
Они позволяют получить выигрыш в силе и менять её направление.
Чем больше в полиспасте подвижных блоков, тем большим будет выигрыш в силе.
Характеристики полиспастов представлены в таблице.
| № | К-во неподвижных блоков | К-во подвижных блоков | Изменение направления силы, раз | Выигрыш в силе, раз | Проигрыш в расстоянии, раз |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 2 | 2 |
| 3 | 1 | 2 | 1 | 3 | 3 |
| 4 | 1 | 3 | 1 | 4 | 4 |
| 5 | 1 | 4 | 1 | 5 | 5 |
| 6 | 1 | 5 | 1 | 6 | 6 |
п.5. «Золотое правило» механики для гидравлического пресса
Подробней о гидравлическом прессе – см. §30 данного справочника.
Работы малого и большого поршня равны.
Таким образом, «золотое правило» для гидравлического пресса также выполняется.
Гидравлический пресс не дает выигрыша в работе.
п.6. «Золотое правило» механики для наклонной плоскости
В любом случае тело, оказавшись в точке B, приобретает потенциальную энергию \begin
Получаем \begin
Наклонная плоскость не дает выигрыша в работе.
Выигрыш в силе компенсируется проигрышем в расстоянии.
Выигрыш в силе равен отношению длины наклонной плоскости к высоте.
Например, из пяти наклонных плоскостей, представленных на рисунке, наибольший выигрыш в силе даст плоскость 5, т.к. у нее отношение \(\frac Lh\) максимально (угол наклона минимален).
В реальности, если учесть силу трения, этот выигрыш уменьшается, т.к. с уменьшением угла наклона сила трения растет.
п.7. Задачи
Задача 1. Груз весом 200 Н равномерно поднимают по наклонной плоскости на высоту 5 м, прикладывая силу 100 Н. Найдите длину наклонной плоскости. Трением можно пренебречь.
Работы при подъеме тела вверх и при перемещении вдоль наклонной плоскости равны: \(A=Ph=FL\). Получаем \begin
Задача 2. При штамповке детали больший поршень гидравлического пресса поднялся на 1 см, а меньший поршень опустился на 20 см. Какая сила действовала на деталь, если на малый поршень действовала сила 500 Н.
Работы по перемещению поршней равны: \begin
Задача 3. К концам рычага длиной 1 м подвешены грузы массой 8 кг и 12 кг. На каком расстоянии от середины рычага должна быть точка опоры, чтобы рычаг находился в равновесии? Ответ запишите в сантиметрах.
Плечо для груза 1: \begin
Задача 4. Если груз лежит на левой чашке неравноплечих весов, его уравновешивают гири массой \(m_1=2\ \text<кг>\) на правой чашке. Если же груз положить на правую чашку, его уравновесит только одна гиря массой \(m_2=0,5\ \text<кг>\) на левой чашке. Какова масса \(m\) груза? Во сколько раз одно плечо весов длиннее другого?
Пусть длина правого плеча \(L_1\), левого плеча – \(L_2\).
По условию задачи \begin
Ответ: 1 кг; левое плечо длиннее правого в 2 раза
Задача 5*. Прямолинейный кусок проволоки массой \(m=40\ \text<г>\) подвешен за середину. Левую половину куска согнули, как показано на рисунке. Какой массы груз надо подвесить в точке A, чтобы восстановить равновесие.
Пусть длина всей проволоки \(L\).
Тогда расстояние от центра тяжести проволоки слева до точки подвеса \(OK=L/4\), а расстояние от центра тяжести проволоки справа до точки подвеса \(OE=L/2\).
Груз массой \(M\) подвешен на расстоянии \(OA=L/2\).
Из ПРАВИЛА моментов получаем: \begin
Сокращаем на \(gL\) \begin
Задача 6*. Балка массой 1200 кг и длиной 3 м лежит на опорах, равноудаленных от ее концов. Расстояние между опорами 2 м.
Какую силу, перпендикулярную балке и направленную вертикально вверх нужно приложить, чтобы приподнять балку за один из её краёв?