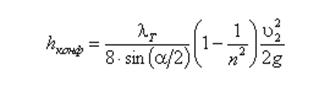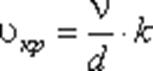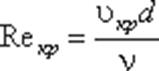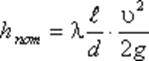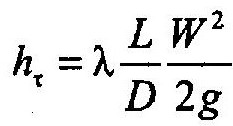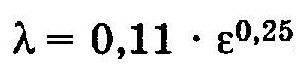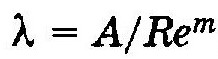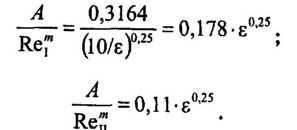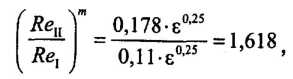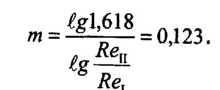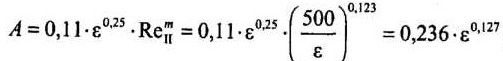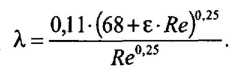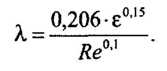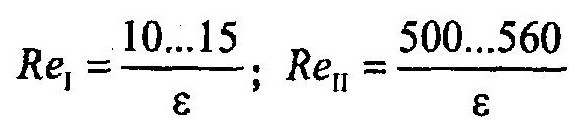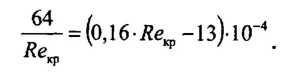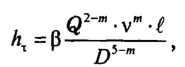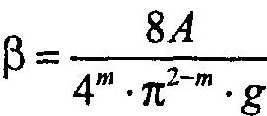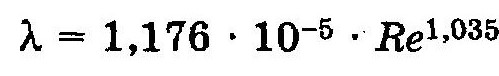Чем в общем случае обуславливается потеря напора при движении жидкости в трубопроводе
Основы гидравлики
Гидравлические сопротивления и их расчет
Виды гидравлических сопротивлений
Таким образом, потери напора при движении жидкости складываются из потерь напора на трение и потерь на местные сопротивления, т. е.:
Потери напора при равномерном движении жидкости в трубах
Найдем общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов.
Если выделить на участке трубы с равномерно текущей жидкостью два произвольных сечения 1 и 2, то потери напора при перемещении жидкости между этими сечениями можно описать при помощи уравнения Бернулли:
где:
z1 и z2 – перепад высот между центрами соответствующих сечений;
p1 и p2 – давление жидкости в соответствующих сечениях;
γ – удельная плотность жидкости, γ = gρ ;
hтр – величина потерянной энергии (потери на трение).
Из этой формулы выразим величину потерянной энергии hтр :
Это выражение называют уравнением равномерного движения жидкости в трубопроводе. Если труба расположена горизонтально, т. е. перепад высот между ее сечениями отсутствует, то уравнение примет упрощенный вид:
Формула Дарси-Вейсбаха для равномерного движения жидкости в трубах
где:
λ – коэффициент гидравлического трения (величина безразмерная);
g – ускорение свободного падения.
Для труб произвольного сечения в формуле Дарси-Вейсбаха используют понятие приведенного или эквивалентного диаметра сечения трубы по отношению к круглому сечению.
В некоторых случаях используют также формулу
Потери напора из-за местных сопротивлений
Потери напора в местных сопротивлениях hм (местные потери напора) вычисляют по формуле Вейсбаха :
где:
v – средняя скорость в сечении, расположенном ниже по течению за местным сопротивлением;
ξ – безразмерный коэффициент местного сопротивления, определяемый для каждого вида местного сопротивления по справочным таблицам или установленным зависимостям.
Потери напора при внезапном расширении трубопровода находят по формуле Борда :
где v1 и v2 – средние скорости течения до и после расширения.
При внезапном сужении трубопровода коэффициент местного сопротивления определяется по формуле:
При резком повороте трубы круглого поперечного сечения на угол α коэффициент сопротивления можно найти по формуле:
Аналогичными методами осуществляют подбор или расчет коэффициентов сопротивления для других видов местных сопротивлений – резкое или постепенное сужение (расширение) трубопровода, повороты, входы и выходы из трубы, диафрагмы, запорные устройства, сварочные швы и т. п.
Приведенные выше формулы применимы для турбулентного режима движения жидкостей с большими числами Рейнольдса, когда влияние вязкости жидкости незначительно.
При движении жидкости с малыми числами Рейнольдса (ламинарный режим) величина местных сопротивлений мало зависит от геометрических характеристик сопротивления и скорости потока, на их величину большее влияние оказывает величина числа Рейнольдса.
В таких случаях для расчета коэффициентов местных сопротивлений применима формула А. Д. Альтшуля :
Значения параметра А и некоторых местных сопротивлений приводятся в справочных таблицах и используются при практических расчетах трубопроводов, предназначенных для движения жидкостей в ламинарном режиме.
Гидравлические потери напора при течении жидкости по трубопроводу
Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов (рассмотрены в п.4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.
1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.
2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).
4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис.4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение
5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис.4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле
6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζотв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.
22. Турбулентное движение жидкости. Распределение скоростей.
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической υ кр.
Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.
Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Reкр и определяется следующим образом:
Как показывает опыт, для труб круглого сечения Reкр примерно равно 2300.
Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re Reкр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.
При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рис. 4.6. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.
Рис. 4.6. Модель турбулентного режима движения жидкости
23. Потери напора при турбулентном движении жидкости по трубопроводу. Способы их определения.
Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:
Впервые наиболее исчерпывающей работы по определению были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости lg(1000λ) от lg Re для ряда значений Δ/r 0. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на рис. 4.7, где построены кривые зависимости lg (1000λ) от lg Re для ряда значений Δ/r0.
Прямая I соответствует ламинарному режиму движения жидкости.
Далее на графике можно рассматривать три области.
Таким образом, ламинарное и турбулентное движение представляют два различных вида движения. Они отличаются не только характером движения частиц, но также особенностями распределения скоростей по сечению и видом зависимости между гидравлическим сопротивлением и скоростью.
5. ПОТЕРИ НАПОРА ПРИ ДВИЖЕНИИ ЖИДКОСТИ
При течении реальной жидкости возникают силы сопротивления, обусловленные вязкими напряжениями. Эти силы производят работу, которая целиком превращается в тепловую энергию. Следовательно, при течении жидкости происходит процесс необратимого превращения части механической энергии во внутреннюю энергию. Работа сил вязкости, произведенная между двумя сечениями потока и отнесенная к единице веса движущейся жидкости, называется потерями напора 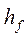
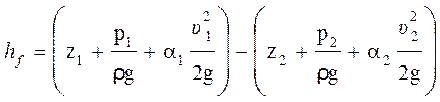
где 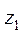
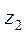
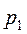
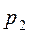
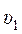
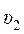
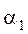
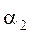
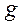
Потери напора при движении жидкости складываются из потерь напора на трение 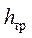
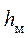
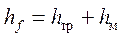
5.1. Потери напора на трение
Потери напора на трение, или потери по длине, возникают в чистом виде в прямых трубах постоянного сечения, т. е. при равномерном течении жидкости. Для горизонтальной трубы постоянного сечения (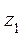
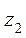
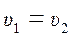
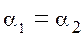
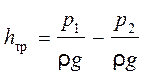
Таким образом, при равномерном движении жидкости потери напора по длине трубы определяются разностью пьезометрических высот в сечениях.
Общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов, имеет вид
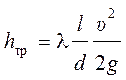
где 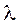
Эта зависимость называется формулой Дарси-Вейсбаха.
5.2. Понятие шероховатости поверхности
Для грубой количественной оценки шероховатости используется понятие средней высоты выступов. Эта высота, измеряемая в линейных единицах, называется абсолютной шероховатостью и обозначается обычно буквой Δ.
При одной и той же величине абсолютной шероховатости влияние ее на величину гидравлических сопротивлений различно в зависимости от диаметра трубы. Поэтому вводится понятие относительной шероховатости, измеряемой отношением абсолютной шероховатости к диаметру трубы, т. е. Δ/d.
Кроме того, даже при одной и той же абсолютной шероховатости и одинаковом диаметре трубы из разного материала могут иметь совершенно различное сопротивление в зависимости от формы выступов, густоты и характера их расположения и т. д. Учесть это влияние непосредственными измерениями практически невозможно. В связи с этим в практику гидравлических расчетов было введено представление об эквивалентной разнозернистой шероховатости Δэ. Под эквивалентной шероховатостью понимают такую высоту выступов шероховатости, сложенной из песчинок одинакового размера, которая дает одинаковую с заданной шероховатостью величину коэффициента гидравлического трения λ.
5.3. Коэффициент гидравлического трения
При ламинарном движении расчетная зависимость для 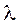
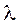
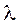
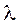
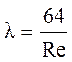
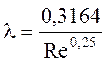
Чтобы распечатать файл, скачайте его (в формате Word).
Почему возникает потеря давления в трубопроводе и как этого можно избежать
Каждый человек, решивший самостоятельно обустроить водоснабжения своего дома, должен быть готов к такой проблеме, как уменьшение напора внутри системы. Как правило, причина кроется в том, что падает общее давление воды в трубе: именно поэтому подбор мощности скважинного насоса должен осуществляться с особой тщательностью.
Почему падает напор в водопроводе
Когда жидкость двигается по трубопроводу, она встречает определенные препятствия на своем пути.
На внутреннее сопротивление водопровода оказывают влияние такие факторы:
Следует сказать, что даже если речь идет о транспортировке воды по прямой трубе, все равно определенное торможение ее потока наблюдается. Чем более увеличивается протяженность водовода, тем более возрастает показатель суммарного сопротивления.
Потеря давления в прямых трубопроводах
Чтобы точно произвести необходимые расчеты, удобнее всего применить особые таблицы и формулы: они позволят получить наиболее точные параметры. Следует также взять во внимание, что питающие водопроводы в последнее время в основном монтируются из полимерных труб. Падение давления в трубопроводе данного типа наблюдается в заметно меньших масштабах.
Для данных изделий характерны следующие эксплуатационные преимущества:
Как учитывать местные сопротивление
Наряду с линейными потерями внутри трубопроводов могут иметься так называемые «местные» сопротивления. Речь идет прежде всего об элементах, обеспечивающих разветвление и управление мощностью потока – тройниках, кранах, вентилях, угловых коленах, клапанах и т.п. На параметры потери внутри этих изделий влияет скорость потока жидкости и их конфигурация. Читайте также: «Какое должно быть давление в трубах водоснабжения – правила расчета».
Формула, по которой рассчитывается внутреннее сопротивление
Как определить потери напора в трубопроводе? Расход воды определяется такой формулой: Q = V×S. Расход воды здесь обозначается, как «Q» (м3/сек), площадь сечения трубы – как «S». Для обозначения скорости здесь используется буква «V» (м/сек). Для вычисления площади сечения используется классическая формула S = π×D2/4, где под «D» понимается диаметр водопроводной трубы. Читайте также: «Как рассчитать расход воды по диаметру трубы – теория и практика».
Когда расчеты искомых величин будут закончены, можно прийти к выводу о мизерности показателей местного сопротивления, при сравнении с общими (суммарными) потерями, вне зависимости от того, какие именно образцы используются. Сопротивление воды в трубах может немного возрасти, если повысить скорость потока: это происходит из-за того, что водный канал по своей узкой части начинает пропускать большой объем воды.
Потери воды в трубопроводах могу возрасти до значительных показателей. Чтобы этого не происходило, рекомендуется изначально комплектовать водопроводы изделиями с большим диаметром: впоследствии некоторые дополнительные финансовые траты с лихвой компенсируются. Это даст возможность вообще отказаться от учета местного сопротивления. Если же говорить об общих ситуациях, то параметры потери в водопроводной системе вычисляются с учетом расхода 2-4 м3 жидкости для местных сопротивлений. Когда приходится учитывать потери при прохождении прямолинейных участков, то уровень суммарных потерь может достигать примерно 5 м3.
Расчет потерь напора в трубопроводах
В процессе течения нефтепродуктов имеют место потери напора на трение hτ и местные сопротивления hMC.
Потери напора на трение
Потери напора на трение при течении ньютоновских жидкостей в круглых трубах определяются по формуле Дарси—Вейсбаха
где λ — коэффициент гидравлического сопротивления; L, D — соответственно длина и внутренний диаметр трубопровода; W — средняя скорость перекачки; g — ускорение силы тяжести.
Величина коэффициента гидравлического сопротивления λ в общем случае зависит от числа Рейнольдса Re = W • D/v и относительной шероховатости труб ε = kэ/D (здесь v — кинематическая вязкость нефтепродукта при температуре перекачки; кэ — эквивалентная шероховатость стенки трубы).
При ламинарном режиме перекачки (Re = ReKp) расчет λ выполняется по формуле Стокса
Эквивалентная шероховатость kэ стальных труб
С незначительной коррозией после очистки
После нескольких лет эксплуатации
Сильно заржавленные или с большими отложениями
В зоне гидравлически гладких труб турбулентного режима (ReKp ReII) расчет λ обычно ведут по формуле Шифринсона
Нетрудно видеть, что формулы Стокса, Блазиуса и Шифринсона могут быть представлены зависимостью одного вида
где А, т — коэффициенты, величина которых для каждой зоны трения неизменна.
Однако формула Альтшуля к этому виду не приводится. Это исключает возможность решения гидравлических задач в общем виде.
Ту же задачу можно было решить следующим образом. При Re = ReI еще справедлива формула Блазиуса, а при Re = RеI уже можно пользоваться формулой Шифринсона. Учитывая, что переходные числа Рейнольдса Альтшулем рекомендовано находить по формулам:
для зоны смешанного трения получаем:
Поделив почленно получим:
Различие в выражениях для расчета коэффициента А объясняется тем, что в первом случае не было сделано необходимое алгебраическое преобразование
Среднеквадратичная погрешность аппроксимации В.ДБелоусова по сравнению с формулой Альтшуля составляет около 5%. Связано это, в частности, с тем, что ее автор не стремился сделать погрешность вычислений минимальной, а исходил из условия равенства коэффициентов X на границах зоны смешанного трения и соседних зон.
Автору совместно с аспиранткой Н.В. Морозовой удалось свести уравнение Альтшуля к виду со среднеквадратичной погрешностью 2,6%. Это было сделано следующим образом.
Представим формулу Альтшуля в виде
Недостатком данной записи является то, что расчетный коэффициент 0,11(68 + ε · Re) °- 25 является функцией числа Рейнольдса. Вместе с тем из формул следует, что в зоне смешанного трения справедливо неравенство
Подставив его получили искомую зависимость
Из нее видно, что в зоне смешанного трения турбулентного режима величины коэффициентов А и т равны 0,206 • е 0,15 и 0,1 соответственно. Среднеквадратичная погрешность расчетов по формуле относительно формулы Альтшуля — менее 3%, что меньше, чем по другим известным аппроксимациям.
Следует подчеркнуть, что учет наличия переходной зоны приводит к изменению критического числа Рейнольдса. Кроме того, А.Д. Альтшуль, строго говоря, для переходных чисел Рейнольдса рекомендует диапазоны
Рассуждая аналогично, можно найти все остальные характерные числа Рейнольдса. Приравняв формулы Гипротрубопровода и Блазиуса, получаем Reкp = 2800. Из равенства правых частей формулы Блазиуса и формулы находим, что ReI = 17,5/ε. Наконец, приравняв правые части формулы и формулы Шифринсона, несложно найти, что ReII = 531/ε.
В тех случаях, когда необходимо, чтобы зависимость потерь напора на трение от расхода Q была выражена в явном виде, удобно использовать обобщенную формулу Лейбензона
Учитывая, что формулу Гипротрубопровода можно привести к виду
Рекомендуемые величины коэффициентов А, β и m