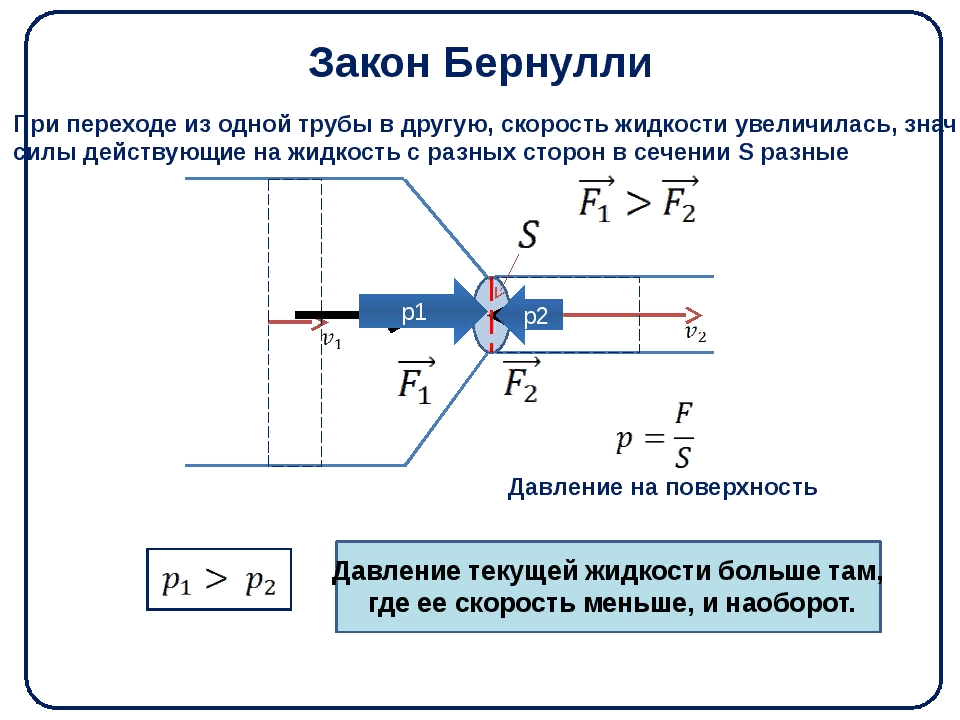
Чем выше давление тем выше скорость

Чем выше давление тем выше скорость

В этом параграфе мы применим закон сохранения энергии к движению жидкости или газа по трубам. Движение жидкости по трубам часто встречается в технике и быту. По трубам водопровода подается вода в городе в дома, к местам ее потребления. В машинах по трубам поступает масло для смазки, топливо в двигатели и т. д. Движение жидкости по трубам нередко встречается и в природе. Достаточно сказать, что кровообращение животных и человека — это течение крови по трубкам — кровеносным сосудам. В какой-то мере течение воды в реках тоже является разновидностью течения жидкости по трубам. Русло реки — это своеобразная труба для текущей воды.

Как известно, неподвижная жидкость в сосуде согласно закону Паскаля передает внешнее давление по всем направлениям и во все точки объема без изменения. Однако, когда жидкость течет без трения по трубе, площадь поперечного сечения которой на разных участках различна, давление оказывается неодинаковым вдоль трубы. Выясним, почему давление в движущейся жидкости зависит от площади поперечного сечения трубы. Но сначала ознакомимся с одной важной особенностью всякого потока жидкости.

Предположим, что жидкость течет по горизонтально расположенной трубе, сечение которой в разных местах различное, например по трубе, часть которой показана на рисунке 207.

Если бы мы мысленно провели несколько сечений вдоль трубы, площади которых соответственно равны и измерили бы количество жидкости, протекающей через каждое из них за какой-то промежуток времени то мы обнаружили бы, что через каждое сечение протекло одно и то же количество жидкости. Это значит, что вся та жидкость, которая за время проходит через первое сечение, за такое же время проходит и через третье сечение, хотя оно по площади значительно меньше, чем первое. Если бы это было не так и через сечение площадью за время проходило, например, меньше жидкости, чем через сечение площадью то избыток жидкости должен был бы где-то накапливаться. Но жидкость заполняет всю трубу, и накапливаться ей негде.

Как же может жидкость, протекшая через широкое сечение, успеть за такое же время «протиснуться» через узкое? Очевидно, что для этого при прохождении узких частей трубы скорость движения должна быть больше, и как раз во столько раз, во сколько раз площадь сечения меньше.

Действительно, рассмотрим некоторое сечение движущегося столба жидкости, совпадающее в начальный момент времени с одним из сечений трубы (рис. 208). За время эта площадка переместится на расстояние которое равно где — скорость течения жидкости. Объем V жидкости, протекшей через сечение трубы, равен произведению площади этого сечения на длину

В единицу же времени протекает объем жидкости —

Объем жидкости, протекающей в единицу времени через сечение трубы, равен произведению площади поперечного сечения трубы на скорость течения.

Как мы только что видели, этот объем должен быть одним и тем же в разных сечениях трубы. Поэтому, чем меньше сечение трубы, тем больше скорость движения.

Сколько жидкости проходит через одно сечение трубы за некоторое время, столько же ее должно пройти за такое

же время через любое другое сечение.

При этом мы считаем, что данная масса жидкости всегда имеет один и тот же объем, что она не может сжаться и уменьшить свой объем (о жидкости говорят, что она несжимаема). Хорошо известно, например, что в узких местах реки скорость течения воды больше, чем в широких. Если обозначить скорость течения жидкости в сечениях площадями через то можно написать:

Отсюда видно, что при переходе жидкости с участка трубы с большей площадью сечения на участок с меньшей площадью сечения скорость течения увеличивается, т. е. жидкость движется с ускорением. А это по второму закону Ньютона означает, что на жидкость действует сила. Что это за сила?

Этой силой может быть только разность между силами давления в широком и узком участках трубы. Таким образом, в широком участке давление жидкости должно быть больше, чем в узком участке трубы.

Это же следует из закона сохранения энергии. Действительно, если в узких местах трубы увеличивается скорость движения жидкости, то увеличивается и ее кинетическая энергия. А так как мы приняли, что жидкость течет без трения, то этот прирост кинетической энергии должен компенсироваться уменьшением потенциальной энергии, потому что полная энергия должна оставаться постоянной. О какой же потенциальной энергии здесь идет речь? Если труба горизонтальна, то потенциальная энергия взаимодействия с Землей во всех частях трубы одна и та же и не может измениться. Значит, остается только потенциальная энергия упругого взаимодействия. Сила давления, которая заставляет жидкость течь по трубе, — это и есть упругая сила сжатия жидкости. Когда мы говорим, что жидкость несжимаема, то имеем лишь в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление упругих сил, неизбежно происходит. Эти силы и создают давление жидкости. Вот это сжатие жидкости и уменьшается в узких частях трубы, компенсируя рост скорости. В узких местах труб давление жидкости должно быть поэтому меньше, чем в широких.

В этом состоит закон, открытый петербургским академиком Даниилом Бернулли:

Давление текущей жидкости больше в тех сечениях потока, в которых скорость ее движения меньше, и,

наоборот, в тех сечениях, в которых скорость больше, давление меньше.

Как это ни покажется странным, но когда жидкость «протискивается» через узкие участки трубы, то ее сжатие не увеличивается, а уменьшается. И опыт хорошо это подтверждает.

Если трубу, по которой течет жидкость, снабдить впаянными в нее открытыми трубками — манометрами (рис. 209), то можно будет наблюдать распределение давления вдоль трубы. В узких местах трубы высота столба жидкости в манометрической трубке меньше, чем в широких. Это означает, что в этих местах давление меньше. Чем меньше сечение трубы, тем больше в ней скорость течения и меньше давление. Можно, очевидно, подобрать такое сечение, в котором давление равно внешнему атмосферному давлению (высота уровня жидкости в манометре будет тогда равна нулю). А если взять еще меньшее сечение, то давление жидкости в нем будет меньше атмосферного.

Такой поток жидкости можно использовать для откачки воздуха. На этом принципе действует так называемый водоструйный насос. На рисунке 210 изображена схема такого насоса. Струю воды пропускают через трубку А с узким отверстием на конце. Давление воды у отверстия трубы меньше атмосферного. Поэтому

газ из откачиваемого объема через трубку В втягивается к концу трубки А и удаляется вместе с водой.

Все сказанное о движении жидкости по трубам относится и к движению газа. Если скорость течения газа не слишком велика и газ не сжимается настолько, чтобы изменялся его объем, и если, кроме того, пренебречь трением, то закон Бернулли верен и для газовых потоков. В узких частях труб, где газ движется быстрее, давление его меньше, чем в широких частях, и может стать меньше атмосферного. В некоторых случаях для этого даже не требуется трубы.

Можно проделать простой опыт. Если дуть на лист бумаги вдоль его поверхности, как показано на рисунке 211, можно увидеть, что бумага станет подниматься вверх. Это происходит из-за понижения давления в струе воздуха над бумагой.

Такое же явление имеет место при полете самолета. Встречный поток воздуха набегает на выпуклую верхнюю поверхность крыла летящего самолета, и за счет этого происходит понижение давления. Давление над крылом оказывается меньше, чем давление под крылом. Именно поэтому возникает подъемная сила крыла.

1. Допустимая скорость течения нефти по трубам равна 2 м/сек. Какой объем нефти проходит через трубу диаметром 1 м в течение 1 ч?

2. Измерьте количество воды, вытекающей из водопроводного крана за определенное время Определите скорость течения воды, измерив диаметр трубы перед краном.

3. Каким должен быть диаметр трубопровода, по которому должно протекать воды в час? Допустимая скорость течения воды 2,5 м/сек.

Источник

Чем выше давление тем выше скорость

Взаимосвязь между размерами тела при рождении и уровнем артериального давления у детей и её влияние на развитие организма исследованы весьма подробно [2, 5, 15, 16]. В частности, благодаря существованию этой взаимосвязи возможна коррекция сниженных темпов роста тела у детей за счет изменения системного АД [1].

Известно, что продольный рост тела человека является одним из интегральных показателей его развития. Многие соматические заболевания, приводящие к нарушению развития, тормозят процесс естественного роста тела. Особенно чувствителен процесс роста к дефициту питания, нарушениям в состоянии эндокринной системе, к ряду хромосомных заболеваний. Показано, что заболевания и травмы опорно-двигательной системы могут оказывать как тормозящее, так и стимулирующее влияние на процесс роста, особенно в условиях оперативной компенсации отставания в длине конечностей [7, 9].

В процессе филогенеза выработаны механизмы компенсации задержек роста, связанных с некоторыми заболеваниями. В этой связи хотелось бы уточнить, какие заболевания и травмы и в какой степени способны повлиять на процесс естественного продольного роста тела и его дефинитивные размеры. Особое внимание мы уделяем изменению уровня артериального давления, рассматривая его динамику как один из эффекторов в реализации программы роста. Доказано, что напряжение растяжения тканей, увеличивающееся у детей, перед окончанием продольного роста длинных костей конечностей опосредованно связано с изменением системного артериального давления [1, 12].

Если у детей доказана прямая взаимосвязь АД и продольных размеров тела, то в дальнейшем о такой связи сведений нет. Более того, отмечается склонность к артериальной гипертензии людей гиперстенического телосложения, отличающихся невысоким ростом.

Цель работы – анализ взаимосвязи продольных размеров тела и уровня АД у здоровых и больных людей в различные возрастные периоды и её значения для роста и развития детей.

Материалы и методы исследования

Проанализированы антропометрические показатели 2700 новорожденных и их матерей без отклонений в развитии в МУ «Курганская городская больница № 2», а также размеры тела и показатели развития 100 детей после рождения. Выполнены антропометрические и динамометрические исследования, определение уровня АД у 423 здоровых детей разного пола в возрасте от 7 до 17 лет, у 200 здоровых студентов, 353 практически здоровых обследуемых 25–75 лет. Обследовано 135 юношей 17–26 лет, студентов Курганского государственного университета и призывников, а также 65 девушек 17–20 лет, студенток университета.

Кроме того, обследованы 898 новорожденных и их матерей с асимметричной задержкой роста тела, 233 детей с врожденным отставанием в росте одной из конечностей на величины от 3 до 18 см, 67 детей дошкольного возраста с отклонениями в росте и развитии, связанном с патологией беременности, родов, наследственными заболеваниями, от воспитания которых отказались родители. Обследованы 1080 больных в возрасте от 16 до 75 лет с 1–3 стадиями остеоартроза нижних конечностей.

У всех обследуемых выполнены антропометрические исследования и определен уровень артериального давления. Данные о перенесённых заболеваниях получены на основании соответствующих карт диспансерного учёта.

Результаты исследования и их обсуждение

При сравнительном анализе здоровых рожениц и женщин, у которых выявлена задержки внутриутробного развития (ЗВУР) плода обнаружено, что у больных наблюдался более низкий уровень систолического АД (соответственно 116 ± 1,1 и 108 ± 1,2 мм рт.ст.; р≤0,001). Выявлена взаимосвязь уровня АД женщин и частоты встречаемости задержки внутриутробного развития плода (рис. 1). Чем ближе систолическое давление у женщин к уровню нормы, тем реже встречалась данная патология.

Рис. 1. Зависимость частоты встречаемости ЗВУР плода от уровня системного АД рожениц

Для нормальной скорости роста плода необходим оптимальный уровень АД матери, который соответствует среднему значению общепринятой нормы – 120 и 80 мм рт.ст. (рис. 2).

Рис. 2. Продольные размеры тела новорожденных детей со ЗВУР при различном уровне систолического АД рожениц

У детей с задержкой внутриутробного развития, родившихся в срок, отставание в массе тела компенсировалось в основном в течение первого года жизни. При аномалиях же развития снижена не только масса, но и длина тела. Если в 3 года принять за 100 % нормы выявленную длину тела детей 91,7 ± 0,8 см и массу тела 13,6 ± 0,2 кг, то у детей, от которых отказались родители, эти показатели снижены соответственно до 89 % (p

Источник

Чем выше давление тем выше скорость

В данном посте опишу теорию гидравлики простыми словами, чтобы понимать принципы поведения воды в трубе.
Как показала практика, многие работающие с системами автоматического полива люди, имеют ошибочное представление о поведении воды в трубопроводе. Так что опытным монтажникам думаю так же будет полезна данная статья.

Статическое давление
Статическое давление- характеризует свойства воды когда она в покое т.е она не движется.
Динамическое давление- свойство воды, характеризующее ее при ее движении в заданном направлении по трубопроводу для обеспечения, например полива. Параметры двигающейся воды, с которыми мы будем в дальнейшем иметь дело это расход и давление.
Итак, статическое давление воды мы имеем в закрытой системе (перекрытые клапана) при неподвижном потоке воды. Значения давления в этом случае меняются только с изменением высоты водного уровня. Статическое давление показывает потенциал давления, с которым система сможет работать.
Следует запомнить, что значение статического давления на плоской местности остается постоянным и действующим с одинаковой силой во всех направлениях. Перепады высот оказывают влияние на его значение. Повышение высоты снижает, а снижение высоты повышает уровень статического давления.
Как только мы открываем, клапан или кран, вода начинает двигаться и, в этом случае, мы уже имеем дело с динамическим давлением. В этом случае появляются новые потери давления, а именно потери давления на трение по трубопроводу и местные потери (фитинги, обратные клапана, электромагнитные клапана и т.д.). Шероховатость стенок трубы, турбулентность — вот лишь та малая часть явлений, которые отрицательным образом сказываются на значении давления в трубопроводе при движении воды от магистрали к дождевателям.

Динамическое давление
Динамическое давление или «рабочее давление» отличается от статического тем, что оно зависит от потерь связанных с движением воды, и его необходимо также учитывать, как и изменение статического давления связанного с изменением высоты. Динамическое давление непосредственно связанно с расходом или тем количеством воды, которое проходит по трубе или в месте местного сопротивления.

С увеличением количества воды протекающего по трубопроводу, увеличивается скорость движения потока, увеличивая потери в давлении. Можно найти ряд таблиц с потерями на трение, учитывающих диаметры трубопровода, его материал и скорость потока воды. А также вы всегда сможете найти таблицу местных потерь давления в зависимости от расхода в каталогах производителей поливочного оборудования.

ВАЖНО!!
Самое частое заблуждение и стереотип даже у опытных людей, много лет работающих с системами автоматического полива- это святая вера в то, что ПРИ ПОСЛЕДОВАТЕЛЬНОМ ЗАУЖЕНИЕМ ДИАМЕТРА ТРУБОПРОВОДА- СОХРАНЯЕТСЯ ИЛИ УВЕЛИЧИВАЕТСЯ ДАВЛЕНИЕ. Это не ТАК.
Увеличение скорости течения жидкости при переходе из участка трубы с большей площадью поперечного сечения в участок трубы с меньшей площадью поперечного сечения означает, что жидкость движется с ускорением.
Согласно второму закону Ньютона, причиной ускорения является сила. Этой силой в данном случае является разность сил давления, действующих на текущую жидкость в широкой и узкой частях трубы. Следовательно, в широкой части трубы давление жидкости должно быть больше, чем в узкой.
Закон Бернулли

Скорость потока (м3/ч, л/с), значение с которым вода двигается через компоненты трубопровода системы полива, очень важный фактор в анализе гидравлического расчета. Чем быстрее вода движется по трубе, тем выше потери на трение. Слишком большие скорости потока воды могут, также быть причинами других проблем (гидравлические удары, выход из строя запорного оборудования и т.д.).
Опытным путем и с помощью расчетов установлено, что скорость потока равная 1,5 м/с, является оптимальной для движения воды по пластиковым трубам. Дальнейшее увеличение скорости потока, приводит к непропорциональному увеличению значения потерь давления, порой в разы, что может привести к неприятным последствиям, когда на отдаленных зонах вы будете иметь давление, при котором полив осуществляться будет некорректно. А также, при скоростях меньших или равных 1,5 м/с, в системе снижается вероятность появления повреждений, связанных с гидравлическим ударом.

Напомню, что в сервисе по проектированию систем автоматического полива IRRISketch весь гидравлический расчёт делается автоматически, но знать азы всё равно полезно даже опытным работникам.

Источник

Закон Бернулли для чайников и учёных

Предисловием можно считать «За что физики не любят математиков»: http://proza.ru/2015/11/16/160

«Наука должна быть весёлая, увлекательная и простая. Таковыми же должны быть и учёные» (П.Л. Капица). и преподаватели. Но более всего наука должна быть честная. И «Ни один человек не должен покидать стены наших университетов без понимания того, как мало он знает» (Роберт Оппенгеймер). и как мало знают учёные. А чтобы так оно и было, нужно срезать профессора математической лженауки на первой же лекции. И прежним занудой он уже не будет. Знаю, что говорю, и привожу очередной пример.

Правильный ответ: неподвижные поверхностные манометры на картинке вверху показывают давление потоков, так как для измерения давления в потоках нужны такие манометры или датчики давления, которые находились бы внутри потоков и двигались вместе с ними. Давление внутри потоков, знаете ли, почти всегда статично. Но таких мобильных манометров, которые могли бы быть неподвижными относительно ламинарных потоков, нет в опытах к теме «Закон Бернулли». Однако вывод сделан такой, словно они есть, словно давление внутри потоков уже измерено. «Для физика должно существовать только то, что измерено» (Нильс Бор). а не то, что можно подумать, придумать, недодумать и сосчитать. Сосчитать то, чего нет, может каждый.

А тем-то он и хуже, что никакой научности и сложности для понимания в нём нет. К тому же, давление потока на поперечную поверхность или «скоростной напор» измеряется с помощью Г-образной «трубки Пито», вставляемой в поток загнутым концом навстречу потоку. Отсюда: давление в самом потоке примерно равно среднему арифметическому от показаний «трубки Пито» и «трубки у Бернулли». Более того, в ньютоновской механике уменьшение силы давления на параллельную потоку или телу поверхность с увеличением скорости потока или тела и одновременное увеличение давления потока или тела на поперечную поверхность можно объяснить простым векторным разложением силы давления потока или тела. Чем больше скорость автомобиля, тем меньше его вес и давление на дорожное полотно; чем больше скорость потока, тем меньше его давление на стенки трубы. Пусть пока будет так.

Конечно, наши выводы профессору будут сильно не по нутру. Но если он будет ещё в состоянии что-то говорить и продолжит настаивать на том, что «С увеличением скорости потока давление внутри потока уменьшается», то срежем его вторым вопросом: «Почему причина и следствие в формулировке общепризнанного закона Бернулли переставлены местами?».

Можно короче: «Чем больше падение давления в потоке или на данном участке трубы, тем больше здесь и скорость самого потока». И это будет тривиальный закон потоков, у которого уже есть все пять обязательных признаков новой истины: простота, ясность, универсальность, «предсказательная сила» и антинаучность. Опровергнуть этот закон сможет только тот, кто создаст поток жидкости или газа, движущийся из области пониженного давления в область повышенного давления, то есть против действия превосходящих сил давления и упругости. Шутка.

Инженер-аэродинамист сформулирует свой закон потоков примерно так: «Давление потока на параллельную или отрицательно наклонную поверхность всегда тем меньше давления в самом потоке, чем больше скорость потока или поверхности (верхней поверхности крыла); а давление потока на поперечную или положительно наклонную поверхность всегда тем больше давления в самом потоке, чем больше скорость потока или поверхности (нижней поверхности атакующего крыла)». И это будет качественный закон взаимодействия потоков с поверхностями, так как в каждом конкретном случае величина давления потока на поверхность зависит не только от скорости потока, но и от физических свойств потока и поверхности, поэтому она не вычисляется, а только измеряется. Следовательно, математикам и в аэродинамике делать особо нечего.

Действие этих двух законов во многих опытах и явлениях складывается или накладывается, поэтому наблюдаемый результат нельзя объяснять действием только какого-то одного закона. Но объединённого закона Бернулли или третьего математического закона потоков никогда не было, поэтому как определить «личную долю» каждого закона в результате того или иного опыта к теме «Закон Бернулли» не знает ни один математик. но знает каждый инженер. Он просто измеряет с помощью манометров и динамометров давление в потоке и давление потока при различной скорости потока, а потом лишь сравнивает результаты измерений. и никаких теорий потоков для него словно не существует. Действительно, зачем вычислять, если можно измерить.

Качественный закон потоков гласит: «Давление потока на параллельную ему поверхность всегда тем меньше давления в самом потоке, чем больше скорость этого потока и чем больше хаос в движении частиц пограничного слоя потока». Можно короче: «Давление потока на параллельную поверхность всегда тем меньше, чем больше хаос в движении частиц потока».

В гидродинамике давление всегда первично, а скорость потока вторична; в аэродинамике скорость крыла всегда первична, а давление неподвижной атмосферы на него всегда вторично. Плоское крыло самолёта или птицы не изменяет давление в неподвижной атмосфере, а изменяется с увеличением скорости и угла атаки лишь взаимодействие быстрого крыла с атмосферой. Но в наших рассуждениях крыло чаще всего неподвижно, а это атмосфера «набегает» на крыло, словно всё происходит в аэродинамической трубе или в статическом (стационарном) потоке. Просто так нам удобнее рассуждать и объяснять.

У инженеров всё, что летает, делает это по причине совсем небольшой положительной разницы или асимметрии атмосферного давления на крыло. Появление подъёмной силы как раз и обусловлено качественным законом потоков: «Давление атмосферного потока на верхнюю отрицательно наклонную поверхность быстрого крыла тем меньше давления в самой атмосфере, чем больше хаос и разрежение частиц воздуха над ней; а давление потока на нижнюю положительно наклонную поверхность крыла тем больше атмосферного давления, чем больше скорость крыла, его угол наклона или атаки и деформация или уплотнение упругого воздуха под быстрым крылом». Как диагональ делит прямоугольник на два равных треугольника, так и плоское атакующее крыло делит набегающий поток на две самостоятельные и равнозначные причины возникновения подъёмной силы.

Вспомним, атмосферное давление на уровне моря равно 1,0033 кг/см2. Это очень большая сила, которая давит на неподвижное плоское крыло совершенно одинаково и сверху, и снизу. Если атмосферное давление со стороны одной из поверхностей крыла убрать, то со стороны противоположной поверхности тут же возникнет сила равная 10033 кг/м2. Да, 10 тонн на каждый квадратный метр крыла! И что мы имеем: орёл весом 4 кг, имея площадь «несущих поверхностей» как раз 1м2, почти неподвижно парит в вышине при положительной разнице атмосферных давлений на его крылья всего 0,04% от теоретически возможного 1 кг/см2; АН-2 («кукурузник») летает горизонтально на разности 0,4% атмосферного давления; а скоростному современному пассажирскому авиалайнеру для горизонтального полёта достаточно и 5% от 1 кг/см2 или 50 г/см2.

Идеальный или самый эффективный аэродинамический профиль – это «беспрофиль», то есть плоское, как лезвие безопасной бритвы, крыло. И это для передовых инженеров уже аксиома или «новая аэродинамика», а Природа это знала ещё со времён первых летающих насекомых и птеродактилей. Так вот, асимметричное атмосферное давление на совершенно плоское крыло возникает и при его нулевом угле наклона к вектору движения набегающего атмосферного потока, если верхняя поверхность крыла испещрена микроскопическими неровностями, а нижняя – максимально гладкая. В воде «эффект хаоса над крылом» проявляется ещё значительно сильнее.

Это утверждение доказано самой эволюцией живой природы и передовой практикой авиастроения. Смотрим на расправленное крыло любой птицы: сверху оно бархатистое и может играть всеми цветами радуги, что физику говорит о дисперсии света на мельчайших неровностях на поверхности, а снизу – всегда очень плотное, гладкое и со стальным отливом. Смотрим на современный пассажирский «Боинг»: сверху он словно матовый, а снизу – зеркально гладкий. И пусть та положительная разница в атмосферном давлении на крыло, которая возникает только по причине различного качества покрытия его аэродинамических поверхностей, будет и недостаточной для полёта, но именно она и позволит самолёту или птице лететь горизонтально с меньшим углом атаки, то есть с меньшим лобовым сопротивлением, экономя топливо и силы.

Инженеры «Боинга» говорят, что уже экономят на «эффекте хаоса над крылом» до 7-ми процентов топлива, а это огромные деньги. Смотрите фотографии «Боингов» и читайте по запросу «Аэродинамика Боинг». А наши дурни из Сколково одной краской покрывают весь Боинг. Смотрите по запросу «Красим Боинг». Кожа акулы тоже только кажется гладкой, а на ощупь она сравнима с наждачной бумагой. Шершавая кожа способствует образованию хаоса в пограничном слое воды, что ещё больше уменьшает её давление на быструю акулу. И таких примеров «мильён».

Однако вторым законом потоков объясняются не только опыты к теме «Закон Бернулли», но ещё один раз доказывается нечто совсем другое, позволяющее увидеть истоки математического идеализма в физике и похоронить математическую физику, как науку о природе. «Законы математики, имеющие какое-либо отношение к реальному миру, ненадёжны; а надёжные математические законы не имеют отношения к реальному миру» (А. Эйнштейн). Сейчас мы эту словесную формулу математического идеализма просто-напросто докажем. Вернее, я докажу, а вы. согласитесь.

«Все жидкости и газы на Земле имеют вес и находятся под давлением веса собственных и выше расположенных слоёв» (Архимед). Поэтому все прозрачные жидкости и газы состоят из примерно одинаковых, равноудалённых и условно неподвижных (колеблющихся или дрожащих) частиц, находящихся в состоянии взаимного отталкивания и относительного (или чуткого) равновесия и взаимно отталкивающихся в газах на расстояниях много больших, чем в жидкостях. Отсюда: давление в любой точке водоёма или атмосферы равно напряжению взаимного отталкивания равноудалённых частиц в этой точке, и по силе оно равно весу всех частиц над этой точкой. Уберите атмосферное давление, и капля воды тут же исчезнет, разлетевшись на молекулы, а аквариум с водой словно взорвётся. И повинно в том будет как раз-таки «напряжение взаимного отталкивания равноудалённых частиц». Смотрите по запросу «Современный Архимед. Трактат «О плавающих телах» и «К физике антигравитонов». Там есть опыты, позволяющие буквально увидеть неподвижность колеблющихся частиц в жидкостях и в газах. Особенно показателен опыт по мгновенному замерзании переохлаждённой воды при её встряхивании в пластиковой бутылке. Многие его знают, но не понимают.

Способность атомов и молекул к движению взаимного отталкивания пропорциональна температуре. А температура – это «опосредованное мерило» интенсивности атомных и внутриатомных движений и величины гравитационных моментов (квантов, импульсов) атомов, передающихся от атома к атому путём индукции.

И ещё. Всем теоретикам и преподавателям на засыпку: «Какой теорией руководствовались братья Райт, когда делали свой воздушный винт, который у них получился с КПД 78-80%, если научной аэродинамики ещё не было, а КПД самых современных пропеллеров из дерева не превышает 85%?».

Хотелось бы услышать возражения или замечания, но их почему-то нет. Видимо, с тем, что мы живём в эпоху математических лженаук, уже никто не спорит.

Воображеньем прозорливым
К догадкам верным нас несло…
Но сонм учёных кропотливых
Свернул наш поиск — на число.

И лязгом счёта оглушённый
Забыл наш ум — решенья ключ…
Стал слепнуть, в шоры цифр втеснённый.
А был так зряч и так могуч!

Уж цифре памятник построен,
Распята Истина на нём.
Поклонник счёта, жрец и воин
Простёрся ниц перед числом:

Не осознать бедняге в заблужденье,
Как много лжи за ширмой исчисленья!

Источник