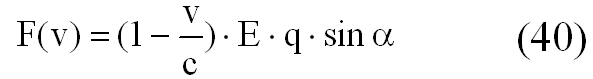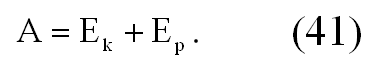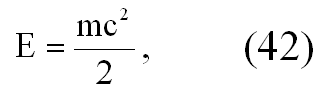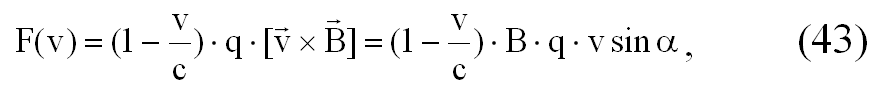Чем выше скорость тем больше масса

14.01.202304.03.2023 admin 0 Comments

15. Масса

С точки зрения классической механики масса тела не зависит от его движения. Если масса покоящегося тела равна m₀, то и для движущегося тела эта масса останется точно такой же. Теория относительности показывает, что в действительности это не так. Масса тела т, движущегося со скоростью v, выражается через массу покоя следующим образом:

Масса — такая же относительная величина, как скорость, время, расстояние. Нельзя говорить о величине массы, пока не будет фиксирована система отсчета, в которой мы изучаем тело.

Из сказанного ясно, что, описывая тело, нельзя просто сказать, что его масса такая-то. Например, предложение «масса шарика 10 г» с точки зрения теории относительности совершенно неопределенно. Численное значение массы шарика ничего еще не говорит нам до тех пор, пока не будет указана инерциальная система, по отношению к которой измерена эта масса. Обычно масса тела задается в инерциальной системе, связанной с самим телом, т. е. задается масса покоя.

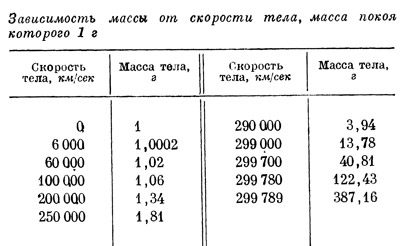
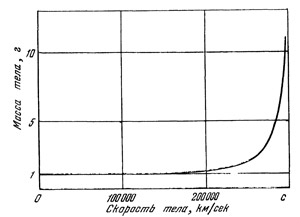
В табл. 6 приведена зависимость массы тела от его скорости. При этом предполагается, что масса покоящегося тела составляет 1 а. Скорости меньше 6000 км/сек в таблице не приводятся, так как при таких скоростях отличие массы от массы покоя ничтожно мало. При больших же скоростях эта разница становится уже заметной. Чем больше скорость тела, тем больше его масса. Так, например, при движении со скоростью 299 700 км/сек масса тела увеличивается уже почти в 41 раз. При больших скоростях даже ничтожное увеличение скорости значительно увеличивает массу тела. Это особенно заметно на рис. 41, где графически изображена зависимость массы от скорости.

Рис. 41. Зависимость массы от скорости (масса покоя тела равна 1 г)

В классической механике изучаются только медленные движения, для которых масса тела совершенно незначительно отличается от массы покоя. При изучении медленных движений массу тела можем считать равной массе покоя. Ошибка, которую мы при этом совершаем, практически незаметна.

Если бы этого не было, то формула (5) потеряла бы всякий смысл, так как деление конечного числа на нуль — недопустимая операция. Конечное число, деленное на нуль, равняется бесконечности — результат, который не имеет определенного физического смысла. Однако мы можем осмыслить выражение «нуль, деленный на нуль». Отсюда и следует, что в точности со скоростью света могут двигаться только объекты, у которых масса покоя равняется нулю. Телами в обычном понимании такие объекты называть нельзя.

Равенство массы покоя нулю означает, что тело с такой массой вообще не может покоиться, а должно всегда двигаться со скоростью с. Объект с нулевой массой покоя, то свет, точнее говоря, фотоны (кванты света). Фотоны никогда и ни в одной инерциальной системе не могут покоиться, они всегда движутся со скоростью с. Тела с массой покоя, отличной от нуля, могут находиться в покое или двигаться с различными скоростями, но с меньшими скоростями света. Скорости света они никогда не могут достигнуть.

Источник

Про смартфон — цены, обзоры и реальные отзывы покупателей

На сайте Pro-Smartfon найдёте отзывы и обзоры топовых смартфонов 2017 года. Всё о плюсах и минусах мобильных телефонов. Свежие фотографии, цены и реальные отзывы покупателей о лучших смартфонах

Чем выше скорость тем больше масса

Здесь легко и интересно общаться. Присоединяйся!

вобще-то у них обратно пропорциональная зависимость

Если вы про релятивистскую динамику, то больше.
Формула зависимости массы от скорости:
M=M0/(КОРЕНЬ ИЗ (1-V^2/C^2))
М0 — масса покоящегося тела, V — скорость тела, C — скорость света.
В случае если скорость нулевая или настолько низкая, что ей можно пренебречь, нижняя часть уравнения примет вид Корень (1-0), то есть просто 1, в итоге будет М=М0
В случае, если скорость объекта близка к скорости света, то в знаменателе будет Корень (1-1), то есть ноль, ну или почти ноль, то есть бесконечно малая величина. При делении Массы на бесконечно малую величину, мы получим бесконечно большую величину.
Итого — чем ближе скорость объекта к скорости света, тем больше его масса.

m = m / √(1 — v 2 /c 2 ) (5)

Отметим сразу же, что скорость, фигурирующая в формуле (5), может быть измерена в любой инерциальной системе. В разных инерциальных системах тело имеет разную скорость, в разных инерциальных системах у него будет также и разная масса.

Рис. 41. Зависимость массы от скорости (масса покоя тела равна 1 г)

Вообще говоря, это не совсем корректно, если не сказать, что совсем не корректно. В физической литературе начала 20 века, когда СТО еще не прижилось в умах людей, использовали понятие массы ‘m’, как отношения энергии ‘E’ на инвариант (квадрата скорости света) ‘c^2’, что отождествляло понятие энергии и массы. Соответственно, чем больше энергия, тем больше т.н. релятивистская масса ‘m’.

С другой стороны, существовало инвариантное понятие массы покоя, соответствующее тому же определению, только энергия бралась в собственной системе отсчета. Делалось это для того, чтобы люди проводили более понятные для себя аналогии с классической физикой.

Позже было понято, что такой подход не особо облегчает дело, и поэтому в современных уже книжках по СТО используют понятие (отдельно) массы покоя и (отдельно) энергии. И в данном случае, энергия ‘E’ не будет равна произведению ‘m0’ — массы покоя — на ‘c^2’.

Так что, ответ на ваш вопрос следующий: масса покоя НЕ зависит от скорости частицы, однако энергия, конечно же, зависит.

С точки зрения же гравитации, как одному из проявлений массы и энергии, там используется т.н. тензор энергии-импульса (что-то типа матрицы), где массе покоя соответствует одна компонента, а энергии движения (импульсу) — другие. Поэтому такое разделение общей энергии и (инвариантной) массы покоя вполне логично.

Источник

МАССА НЕ РАСТЕТ СО СКОРОСТЬЮ!!

МАССА НЕ РАСТЕТ СО СКОРОСТЬЮ!!

Теория относительности, Эйнштейн сначала утверждала, что масса тела растет с увеличением скорости, теперь же отрицает это, но как-то расплывчато, непоследовательно и невнятно.

Авторы (и их статьи) признающие рост массы со скоростью (в хронологическом порядке):

«Масса тела есть мера содержащейся в нем энергии; если энергия изменяется на величину L, то масса меняется соответственно на величину L/(9*10^20) причем здесь энергия измеряется в эргах, а масса — в граммах».
1905 г. Эйнштейн А. Собрание научных трудов. Том 1. стр. 38. «Зависит ли инерция тела (масса) от содержащейся в нем энергии?»
инерция тела растёт с его энергией т1 стр. 397

Гейзенберг 1989 г. «Все частицы состоят из одинаковой субстанции — из энергии».

Современная физика отвергает материализм и признает энергетизм?
=================================================
«Масса любого тела зависит от содержащейся в нем количества энергии. Масса и энергия становятся такими же эквивалентными друг другу величинами, как, например, теплота и механическая работа» 1910 г. Эйнштейн А. Собрание научных трудов. Том 1. стр. 164

«Дорелятивистская физика знала два фундаментальных закона сохранения, а именно:закон сохранения энергии и закон сохранения массы; оба эти фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности слила их в один».
1917 г. Эйнштейн А. Собрание научных трудов. Том 1. стр. 553

«…излучение, испускаемое Солнцем и проходящее через пространство, содержит энергию и поэтому имеет массу; Солнце и все излучающие звезды теряют массу вследствие излучения» [29,179]. Эйнштейн.

Выражение эквивалентности (бред!! Ни в одном учебнике слова эквивалентность нет!!) массы и энергии вошло в науку настолько прочно, что стала символом теории относительности и критерием её практической значимости. Такой точки зрения придерживался не только сам А.Эйнштейн [1], но и другие выдающиеся физики прошлого столетия, такие, как М.Борн (1962), В.Паули (1921), Р.Толмен (1934), Р.Фейнман (1965), В.А.Фок (1955), Е.Тейлор и Дж. Уиллер (1966), не говоря уже об авторах многочисленных учебников, пособий и популярных книг на эту тему.

Цитата из википедии:

Утверждение о том, что масса зависит от скорости, вошло во многие учебные курсы и в силу своей парадоксальности приобрело широкую известность среди неспециалистов. Однако в современной физике избегают использовать термин «релятивистская масса», используя вместо него понятие энергии, а под термином «масса» понимая инвариантную массу (покоя)»

Физическая энциклопедия (т.3=1992 г.) Статья «Масса».

Возникли утверждения, что масса тела растёт с увеличением его скорости. В целом терминология, использующая понятия «М. покоя», «М. движения», ф-лы (11), (12) и т. п. артефакты, мешает понять сущность теории относительности, затрудняет в дальнейшем знакомство с совр. науч. литературой.

Фейнман, Ричард Филлипс (википедия)

1960 г. Масса тела растет с увеличением его скорости.

Большая советская энциклопедия:
Масса частицы (тела) растет с увеличением её скорости. Природа массы — одна из важнейших нерешенных задач современной физики.

Большой энциклопедический словарь ФИЗИКА (1983 г.1998 г.) Статья «Масса».

Чем больше скорость тела, тем больше кинетич. энергия и вместе с тем, как это следует из закона зависимости массы от скорости, тем больше масса тела

Учебник по физике 9 класс:
При увеличении скорости тела его масса не остается постоянной, а растет.

Авторы (и их статьи) отрицающие рост массы со скоростью
(в хронологическом порядке):

Теория Относительности Эйнштейна и ее критика.

Список некоторых оппонентов теории относительности.

Окунь, Лев Борисович (википедия):
2010 г. Университетские профессора, которые позволяют себе говорить, что масса тела растёт с ростом его скорости или импульса вводят в заблуждение школьных преподавателей и их учеников.

2011 г. Эткин. В А. (д. т. н. профессор): Вслед за Окунем Л.Б. утверждаем: Существует единственная масса М, являющаяся мерой колличества вещества, а понятия «массы покоя», «релятивистской». «инертной», «электромагнитной», «гравитационной» и т. п. масс должны быть отброшены как излишние.

ELEMENTY.RU
Есть широко распространенное убеждение, что масса растет со скоростью; ее часто называют «релятивистской массой». Это убеждение основано на неправильной интерпретации связи между энергией и массой: мол, раз с увеличением скорости растет энергия, значит растет и масса. Это утверждение встречается не только во многих популярных книжках, но и в школьных и даже в вузовских учебниках физики.

2014 г. Мамаев А. В. Масса не зависит от скорости.стр.10

2014 г. Мамаев А. В. Масса не зависит от скорости.стр.326

Учебник по физике (школьный):
Масса m, входящая в выражение для импульса, есть фундаментальная характеристика частицы, не зависящая от выбора инерциальной системы отсчета, а, следовательно, и от скорости ее движения. (Во многих учебниках прошлых лет ее было принято обозначать буквой m0 и называть массой покоя. Кроме того, вводилась так называемая релятивистская масса, равная m0/1−β2−−−−−√, зависящая от скорости движения тела. Современная физика постепенно отказывается от этой терминологии)

Академик Гинзбург В. Л. (1916-2009)

Угаров В.А. Специальная теория относительности. М. 1977 г. стр.342 http://www.twirpx.com/file/305036/

Источник

Второй закон Ньютона (Расчёты Примеры)

Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.

В результате чего были выведена новая формула второго закона ньютона а = F /m,

Что такое второй закон Ньютона, масса и вес тела

Обобщая результаты опытов Галилея по падению тяжелых тел, астрономические законы Кеплера о движении планет, данные собственных исследований.

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.

Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.

Ускорение от величины силы

I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at₂) : 2 определим ускорение a.

Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку

Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m . Это отношение назовем массой тела.

Зависимость ускорения от массы

II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).

Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть

Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).

Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):

где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.

Результирующая сила F равна векторной сумме всех сил, приложенных к телу;

Следовательно, сила равна произведению массы на ускорение.

Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение

подставим это выражение в уравнение второго закона Ньютона. Получим

Что такое импульс

Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (т υ ).

Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)

Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содер жащегося в данной теле. Это определение несовершенно.

Из второго закона Ньютона вытекает следующее определение массы. Из равенства

видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость это го тела и наоборот.

Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.

Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:

где m — масса тела, движущегося со скоростью υ; m₀ — масса этого же тела, находящегося в покое; с = 3 • 10 8 м/с скорость света в вакууме.

Проанализируем данное уравнение:

По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.

Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.

Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.

Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.

Масса тела с ростом скорости

Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.

Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.

Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).

Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ₀ = 0) называется свободным падением.

Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.

Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.

Если Р — сила тяжести, m — масса, g — ус корение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м /с 2 ), то применяя второй закон динамики, получим

Выразим с помощью этой формулы веса двух различных тел. Тогда:

Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.

Задачи на второй закон ньютона

Дано:
m = 1000 кг
a = 1 м/с 2

Решение:

Запишем второй закон Ньютона :

F = 1000 кг • 1 м/с 2 = 1000 Н

Ответ: 1000 Н.

2. На мяч действует сила F = 70 Н, масса мяча m = 0,2 кг, найти его ускорение a.

Дано:

Найти:

Решение:

Запишем второй закон Ньютона :

Статья на тему Второй закон Ньютона

6.3. Рост массы в зависимости от скорости

Представление зависимости массы от скорости занимает особое положение в современной физике. История формирования соотношения между массой и энергией изложена В. В. Чешевым в работе [1], где, в частности, сказано: «Представление о возрастании массы электрона было отчасти инициировано гипотезой эфира. В 1881 году Дж. Дж. Томсон, исходя из теоретических соображений, указал, что «электрически заряженное тело из-за магнитного поля, которое оно вызывает, согласно теории Максвелла, так должно вести себя, как будто его масса увеличивается на некоторую величину, зависящую от его заряда и формы». В дальнейшем Томсон показал, что масса движущегося заряда должна возрастать с возрастанием его движения. Опыты Кауфмана закрепили представление о возрастании массы движущегося электрона» [1, c.117].

Это явление как будто проявляется при эксплуатации ускорителей заряженных частиц. Но в ускорителях заряженных частиц наблюдается не изменение массы частиц в зависимости от скорости (это наблюдать невозможно), а необъяснимое в современных физических представлениях изменение ускорения заряженных частиц при контролируемых электрическом и магнитном полях.

Из второго закона Ньютона a = F/m, где а — ускорение, F — сила, m — масса, видно, что ускорение зависит и от силы, и от массы. Поэтому более логичным представляется объяснение наблюдаемого ускорения не ростом массы, а результатом изменения сил взаимодействия электрического и магнитного полей с заряженными частицами, движущимися в этих полях.

Изменение сил взаимодействия определяется конечной скоростью распространения возмущения (изменения) напряженности полей. Неизменность сил взаимодействия при движении взаимодействующих тел возможна только в том случае, если скорость распространения возмущения бесконечна.

Рис. 20

Как бы быстро ни был перемещен заряд q в точку К электрического поля напряженностью Е (рис. 20), созданного заряженными пластинами В и Д, положение, показанное на рис. 21, может иметь место только через конечный интервал времени, определяемый скоростью распространения возмущения в поле Е.

Рис. 21

Полагаем, что взаимодействие поля с заряженной частицей в вакууме происходит со скоростью с, скоростью распространения электромагнитного поля, при этом сохраняется равенство импульса силы моменту количества движения. Тогда сила взаимодействия F (v) электрического поля напряженностью Е и частицы, имеющий заряд q и двигающийся в этом поле со скоростью v, будет равна:

Под воздействием ускоряющего поля возрастает скорость, а вместе с ней кинетическая энергия частицы. При этом происходит определенное изменение конфигурации ускоряющего поля и собственного поля ускоряемой частицы, которое приводит к увеличению ее потенциальной энергии, т. е. переходу потенциальной энергии ускоряющего поля в кинетическую энергию и потенциальную энергию ускоряемого заряда. Полная энергия частицы А, равная qU (U — пройденная разность потенциалов), слагается из ее кинетической энергии — E k и потенциальной — Е p

Кинетическая энергия ускоряемой частицы ограничена пределом

потенциальная же энергия ускоряемой частицы, возможно предела не имеет, пока не виден. Поэтому полная энергия ускоряемой частицы, несмотря на ограничение скорости, продолжает расти и определяется только пройденной разностью потенциалов. Данный процесс обратим, при взаимодействии разогнанной частицы с тормозящим полем происходит освобождение запасенной энергии.

Сила Лоренца — F (v), действующая на движущийся в магнитном поле заряд, определяется аналогичным образом:

Разновидности чувств: любовь, ненависть, злость, апатия.

Чем выше скорость тем больше масса

15. Масса