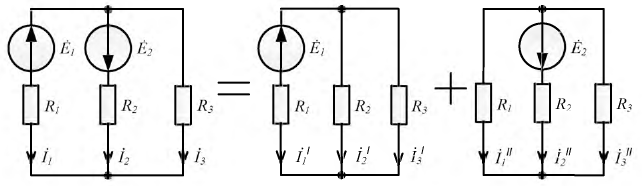
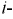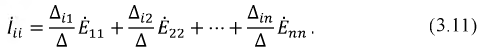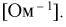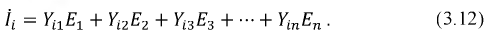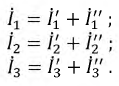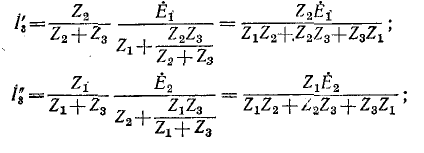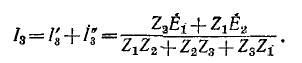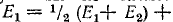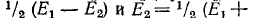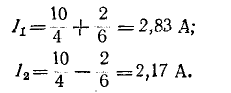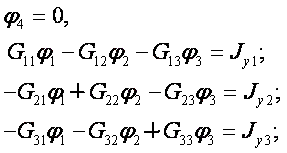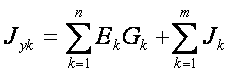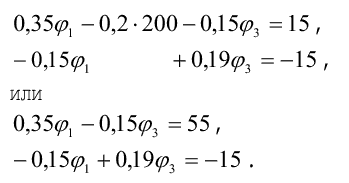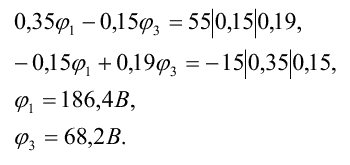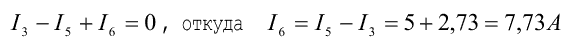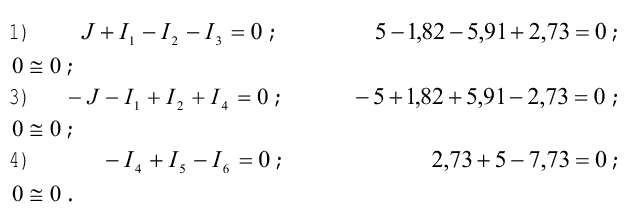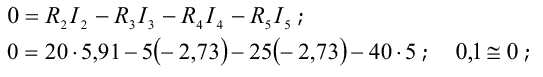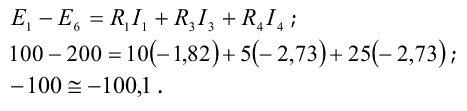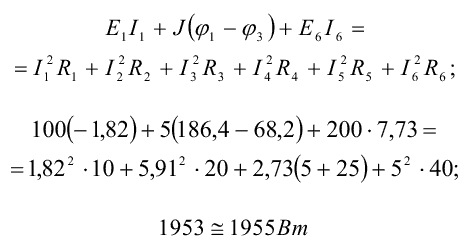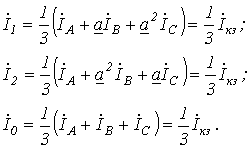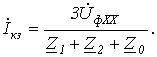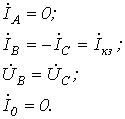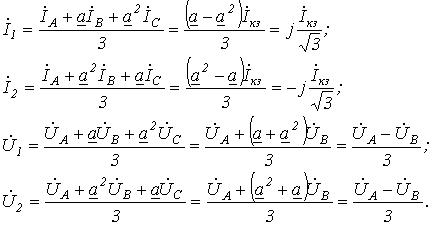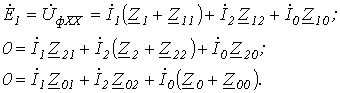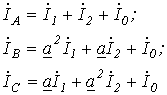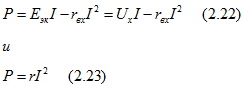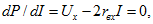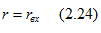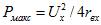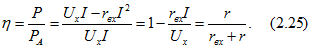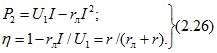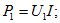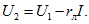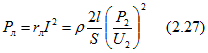Чем заменяется исключаемый источник эдс при расчете методом наложения

1.2 Метод наложения

1.2 Метод наложения

Метод наложения основан на свойстве линейности электрических цепей. Метод наложения справедлив только для линейных цепей. Метод наложения применяется для определения токов в ветвях схемы с несколькими источниками.

Алгоритм метода наложения:

1) выбирают положительные направления токов в ветвях цепи;

2) находят частичные токи в ветвях, вызванные каждым источником по отдельности (схему рассчитывают столько раз, сколько источников действует в схеме);

3) токи в ветвях по методу наложения находят как алгебраическую сумму частичных токов (знак частичного тока при суммировании определяется по положительному направлению тока ветви).

Решение задач методом наложения

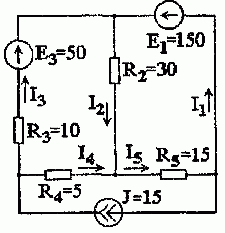
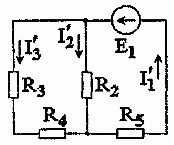
1. Выполним расчет цепи при воздействии источника ЭДС E₁, полагая E₃ = 0, J = 0. Источники считаем идеальными, поэтому внутренние сопротивления ЭДС равны нулю, а источника тока – бесконечности. С учетом этого изобразим расчетную схему (рис. 1.2.2).

Определение токов в полученной схеме будем вести, пользуясь методом эквивалентных преобразований:

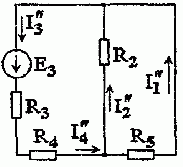
2. Расчет электрической цепи при воздействии ЭДС источника Е₃ выполним, полагая Е₁ = 0, J = 0 (рис. 1.2.3).

В соответствии с рис. 1.2.3 имеем:

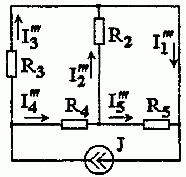
3. Расчет электрической цепи при действии источника тока выполним, полагая E₁ = 0, Е₂ = 0 (рис. 12.4).

В соответствии с рис. 1.2.4 имеем:

Находим токи в параллельных ветвях:

4. В соответствии с принятыми направлениями токов в исходной схеме определим их значения по методу наложения как алгебраическую сумму частичных токов всех промежуточных расчетных схем:

Правильность решения задачи проверяем по первому закону Кирхгофа:

− J + I 3 + I 4 = 0 ; − 15 + 3 + 12 = 0 ; − I 2 − I 4 + I 5 = 0 ; − ( − 0,66 ) − 12 + 11,33 = 0.

Токи I₁ и I₂ получились отрицательными, т.е. их истинное направление в схеме противоположно принятому положительному направлению.

частичные токи, метод наложения

Источник

Принцип и метод наложения

Метод наложения:

Используя метод контурных токов, можно получить обобщённое уравнение по расчёту любого

Сомножитель перед любой ЭДС имеет размерность

Принцип наложения: ток любой 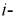ой ветви равен алгебраической сумме токов, созданных каждой из ЭДС цепи в отдельности.

Рис. 3.3. Иллюстрация принципа наложения

На сформулированном принципе базируется метод наложения, суть которого состоит в следующем: в исходной электрической цепи поочерёдно закорачиваются все источники ЭДС, кроме одного, и производится расчет частичных токов в ветвях любым из известных методов. Для определения реальных токов в исходной цепи производится алгебраическое суммирование этих частичных токов:

Метод наложения

В линейной электрической цепи, содержащей источники э. д. с., контурные токи (и соответственно токи в ветвях) представляют собой линейные функции контурных э. д. с. Математически они выражаются формулой (7-4):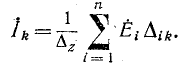

Физический смысл этой формулы заключается в том, что ток в любом контуре линейной электрической цепи может быть получен как алгебраическая сумма токов, вызываемых в этом контуре каждой из э. д. с. в отдельности.

Метод расчета токов, основанный на определении токов в одном и том же контуре (или ветви) при поочередном воздействии э. д. с. и последующем алгебраическом сложении этих токов, называется методом наложения.

При определении частичных слагающих токов по методу наложения необходимо считать включенными внутренние сопротивления тех источников э. д. с., которые принимаются отсутствующими при вычислении слагающих токов. Если в цепи заданы идеальные источники э. д. с., т. е. внутренние сопротивления источников равны нулю, то при определении токов, вызываемых какой-либо э. д. с., все остальные источники э. д. с. закорачиваются.

В свою очередь в линейной электрической цепи, содержащей источники тока, узловые напряжения (и соответственно напряжения на ветвях) представляют собой линейные функции задающих токов источников. Математически они выражаются- формулой (7-6):

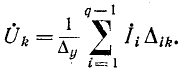
Физический смысл этой формулы заключается в том, что узловое напряжение для любого узла линейной электрической цепи может быть получено как алгебраическая сумма напряжений, вызываемых в этом узле каждым из задающих

токов в отдельности. Таким образом, формула (7-6), так же как и (7-4), представляет собой математическую запись метода наложения, справедливого для линейных электрических цепей.

При определении частичных слагающих узловых напряжений по методу наложения необходимо считать включенными внутренние проводимости тех источников тока, которые принимаются отсутствующими при вычислении слагающих напряжений. Если источники тока заданы без внутренних проводимостей, т. е. проводимости их равны нулю, то при пользовании методом наложения ветви с неучтенными источниками тока разрываются.

Если в линейной электрической цепи заданными являются одновременно источники э. д. с. и источники тока, то метод наложения применим и в этом случае. Например, ток в каком-либо контуре данной цепи может быть получен в результате алгебраического сложения токов, вызываемых в этом контуре поочередным действием источников э. д. с. и тока. При этом отсутствующие источники э.д.с. заменяются внутренними сопротивлениями, а отсутствующие источники тока — внутренними проводимостями.

Пример 7-4.

Пользуясь методом наложения, определить ток в ветви 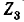схемы рис. 7-4,

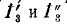
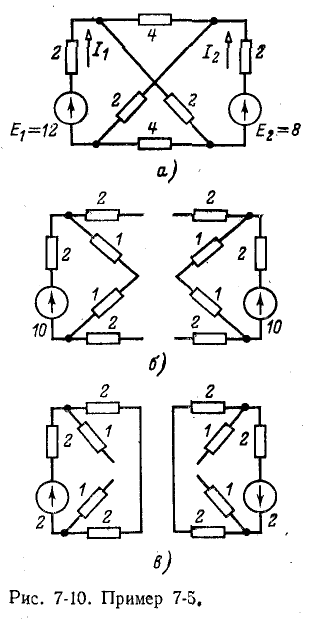
Токи суммируются, а не вычитаются, так как положительные направления их выбраны совпадающими:

Пример 7-5.

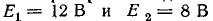
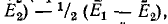
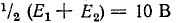
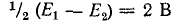
Задана симметричная схема с неравными э. д. с.: (рис. 7-10, а). Значения сопротивлений (в омах) указаны по схеме, тив, что , можно вместо заданной схемы рассмотреть две симметричные схемы, в каждой из которых э. д. с. источников равны. В первой схеме источники имеют э. д. с.и полярность их одинакова; во второй схеме источники имеют э. д. с. и полярность различна.

Пользуясь методикой, описанной, произведем соответствующие рассечения и замыкания накоротко по оси симметрии (рис. 7-10, 6 и в).

Искомые токи найдутся методом наложения:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Расчет электрической цепи методом наложения

Содержание:

Метод наложения

Расчет электрических цепей методом наложения основывается на общем физическом принципе независимости действия сил в линейных системах, так называемом принципе суперпозиций. При помощи этого метода расчет сложной цепи с несколькими эдс сводится к расчету нескольких цепей с одним источником питания.

Ток, в любой ветви, рассматривается как результат наложения токов, получающихся от отдельных эдс, действующих независимо друг от друга.

Порядок расчета цепи методом наложения

1. Заданная схема, в которой предварительно расставляются положительные направления искомых токов, разбивается на подсхемы. При этом в каждой подсхеме оставляется только один источник энергии, остальные заменяются их внутренними сопротивлениями.

2. Рассчитываются частичные токи во всех ветвях каждой подсхемы любым методом.

3. Определяются действительные токи в ветвях исходной схемы путем алгебраического суммирования соответствующих частичных токов. Причем записываются с плюсом тс частичные токи, направление которых совпадает с ранее выбранным направлением тока исходной схемы (см. пункт 1).

4. Производится проверка расчета подсчетом баланса мощностей для исходной схемы.

Возможно вам будут полезны данные страницы:

Пример расчета цепи методом наложения

Условия расчета

Рассчитать цепь, заданную в примере 4.5, методом наложения.

Для решения задачи целесообразно упростить схему заданной цепи (см. рисунок 4.5.2.1), преобразовав ее до двух контуров (см рисунок 4.5.4.4). Рассчитать получившуюся схему методом наложения. Остальные токи найти с помощью законов Кирхгофа, постепенно переходя к исходной схеме.

Схема цепи

Данные для расчета

Расчет

Так как в расчетной цепи, изображенной на рисунке 7.2.2.1,а имеется два источника эдс, разбиваем се на две частичные подсхемы. Расставляем положительные направления токов в схемах и рассчитываем отдельно каждую подсхему, находя частичные токи от действия каждой эдс. Частичные токи в подсхемах можно найти используя закон Ома, преобразование параллельных ветвей и первый закон Кирхгофа.

Расчет подсхемы 7.2.2.1,6 при: , тогда

По первому закону Кирхгофа для узла

Расчет подсхемы 7.2.2.1,в при: тогда

По первому закону Кирхгофа для узла

Действительные токи в ветвях расчетной схемы (см. рисунок 7.2.2.1,а):

Пример задачи с решением 1

Определить токи ветвей схемы с параметрами:

Решение. 1. Приминительно к исходной схеме выбираем условно положительные направления токов

2. Вычерчиваем расчетную схему с одним ИН Ei и определяем частичные токи от действия ЭДС

3. Вычерчиваем расчетную схему с ИН и находим частичные токи:

4. С учетом направлений частичных токов определяем токи в ветвях исходной электрической схемы:

Пример задачи с решением 2

Найти токи в ветвях схемы с параметрами: ,

Частичные токи в схеме, в которой действует только источник ЭДС Е:

Частичные токи в схеме, в которой действует только источник тока J:

Искомые токи ветвей:

Недостатком метода является необходимость повышенной точности расчетов.

Методом наложения нельзя пользоваться для подсчета выделяемых в сопротивлениях мощностей, как суммы мощностей от частичных токов, поскольку мощность является квадратичной функцией тока.

Пусть через R протекают согласно направленные два тока тогда выделяемая мощность:

Она не равна сумме мощностей от частичных токов

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Метод наложения токов. Пример решения

Метод наложения относительно прост, и в основном применяется для не сложных электрических цепей.

Его суть заключается в том, что токи в ветвях определяются как алгебраическая сумма их составляющих от каждого источника. То есть каждый источник тока вносит свою часть в каждый ток в цепи, а чтобы найти эти токи, нужно найти и сложить все составляющие. Таким образом, мы сводим решение одной сложной цепи к нескольким простым (с одним источником).

Порядок расчета

1 – Составление частных схем, с одним источником ЭДС, остальные источники исключаются, от них остаются только их внутренние сопротивления.

2 – Определение частичных токов в частных схемах, обычно это несложно, так как цепь получается простой.

3 – Алгебраическое суммирование всех частичных токов, для нахождения токов в исходной цепи.

Пример решения методом наложения

1. Для начала произвольно выберем направление токов, если в итоге какой либо ток получится со знаком минус, значит нужно изменить направление данного тока на противоположное.

2. Составим частную схему с первым источником ЭДС и рассчитаем частные токи в ней, убрав второй источник. Для удобства частичные токи будем обозначать штрихами.

Свернем схему к одному контуру, с сопротивлением источника и эквивалентным сопротивлением цепи для нахождения тока источника I₁. Для тех, у кого возникают затруднения с нахождением эквивалентного сопротивления рекомендуем прочесть статью виды соединения проводников.

Найдем ток по закону Ома для полной цепи

Найдем напряжение на R 2345

Тогда ток I₃ равен

Определим напряжение на R₂₅

3. Составим частную схему со вторым источником ЭДС

Аналогичным образом вычислим все частичные токи от второй ЭДС

4. Найдем токи в исходной цепи, для этого просуммируем частичные токи, учитывая их направление. Если направление частичного тока совпадает с направлением исходного тока, то берем со знаком плюс, в противном случае со знаком минус.

5. Проверим с правильность решения с помощью баланса мощностей.

Небольшая погрешность связана с округлениями промежуточных значений в ходе выполнения вычислений.

Похожие публикации

Источник

Принцип наложения и метод наложения

Для линейных электрических цепей справедлив принцип наложения, согласно которому ток (напряжение) любой ветви равен сумме частичных токов (напряжений), создаваемых в этой ветви каждым из источников в отдельности. Этот принцип лежит в основе метода наложения. Метод наложения применим только для расчета линейных цепей.

Частичный ток – ток в ветви от действия только одного источника энергии, когда все остальные источники приняты нулевыми. Пусть в цепи действуют nидеальных источников ЭДС и m идеальных источников тока. Тогда ток в i-ой ветви может быть определен как

.

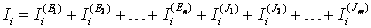
Для удобства использования принципа наложения вводят коэффициентыg_ij и k_ij, определяющие связь тока I_i со значениями источников, так как при действии одного источника ток в линейной цепи пропорционален величине источника:

,

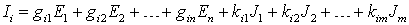
где g_ij – взаимная проводимость ветвей i и j (при j=i g_ij = g_ii называют входной проводимостью ветви i), а k_ij – коэффициент передачи по току между ветвями i и j.

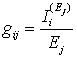
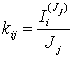
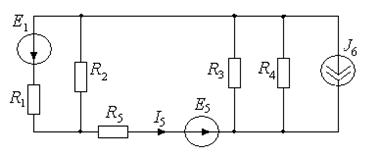
Взаимная проводимость (коэффициент передачи по напряжению) g_ijопределяется как отношение тока в ветви i, обусловленного действием ЭДС E_jк величине этой ЭДС при условии, что остальные ЭДС и токи источников тока цепи равны нулю: . Коэффициент передачи по току k_ij определяется как отношение тока в ветви i, обусловленного действием источника тока J_j к току источника при условии, что остальные источники ЭДС и токи источников тока равны нулю: . Определить частичные токи и соответственно коэффициенты можно по частичным схемам. Используя расчетные коэффициенты можно решать не только задачи прямого анализа электрических цепей, но и обратные задачи, в которых часть параметров цепи с известной топологией неизвестна и подлежит определению, а в число известных параметров могут быть включены токи и напряжения некоторых ветвей цепи.

Пример 6. Определить ток I₅, применив метод наложения. Определить значение ЭДС Е₁, при котором I₅=0.

Решение. По методу наложения .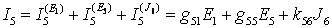

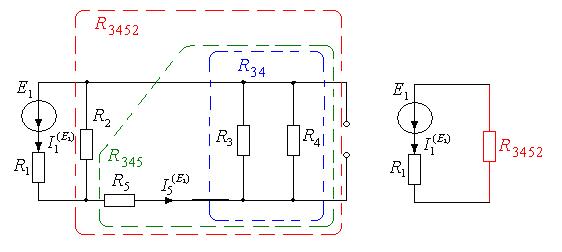
Частичная схема для расчета частичных токов от источника Е₁ (Е₅ = 0,J₆ = 0):

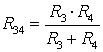
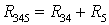
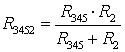
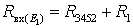
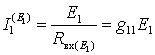
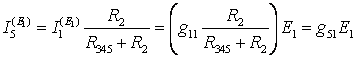
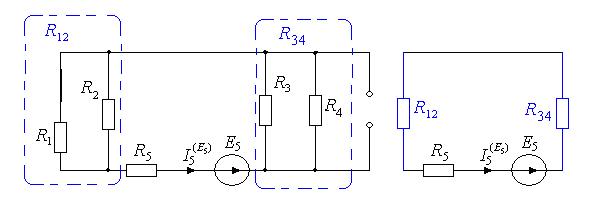
Применим эквивалентные преобразования: _{h«sub>(параллельное соединение резисторов), (последовательное соединение), (параллельное соединение). Входная проводимость 1-ой ветви , где входное сопротивление 1-ой ветви . Частичный ток в ветви с источником . По формуле разброса .}

Частичная схема для расчета частичных токов от источника Е₅ (Е₁=0,J₆=0):

Применим эквивалентные преобразования: , (параллельное соединение резисторов). Входная проводимость 5-ой ветви , где входное сопротивление , тогда .

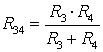
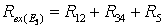
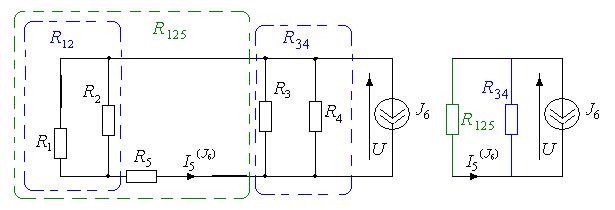
Частичная схема для расчета частичных токов от источника J₆ (Е₁ = 0,Е₅ = 0):

Применим эквивалентные преобразования: , (параллельное соединение резисторов), (последовательное соединение). Напряжение на источнике тока , где , тогда частичный ток .

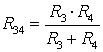
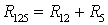
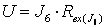
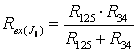
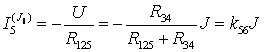
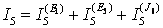
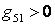
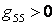
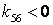
Сумма частичных токов: , коэффициенты передачи , , .

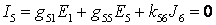
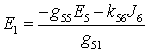
Результат наложения частичных токов равен нулю, т.е. , если при неизменности параметров остальных элементов значение ЭДС будет равно .

9. При расчете электрической цепи методом узловых потенциалов определяются потенциалы узлов цепи, а затем по закону Ома токи в ее ветвях. Метод целесообразно применять в тех случаях, когда число узлов цели меньше или равно числу независимых контуров этой цепи.

Так, для электрической цепи, имеющей четыре узла, составляется три расчетных уравнения (например, для узлов 1, 2 к 3 потенциал узла 4 принимается равным нулю):

Под знаком первой суммы произведения ЭДС ветвей, присоединенных к К-му узлу, на проводимости этих ветвей учитывается ЭДС с положительным (отрицательным) знаком, если она направлена к К-му узлу (от К-го узла). Под знаком второй суммы со знаком «+» («-«) учитываются токи источников тока, которые направлены к К-му узлу (от К-го узла).

Если в цепи между двумя узлами включен идеальный источник ЭДС (внутреннее сопротивление которого равно нулю), необходимо принимать равным нулю потенциал одного из его зажимов, тогда потенциал другого зажима источника будет равен ЭДС с
соответствующим знаком, а количество расчетных уравнений сократится.
Последовательность расчета цепи методом узловых, потенциалов рас-
смотрим на примере. Параметры цепи считаются заданными.

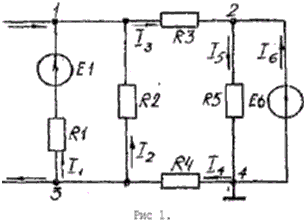
ПРИМЕР 1: Определить токи в ветвях цепи (рис. 1) методом
узловых потенциалов. Положительные направления токов принять по рисунку

E1 = 100В R1 = 10 Ом
E6 = 200В R2 = 20 Ом
I = 5А R3 = 5 Ом R4 = 25 Ом R5 = 40 Ом

1. В заданной цепи четыре узла. Приравняем нулю (заземлим) потенциал узла 4. Тогда ф4 = 0

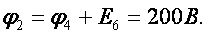
2. Составим расчетную систему уравнений для узлов, потенциалы которых подлежат определению:

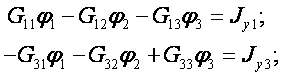
Для узлов 2 и 4 уравнения не составляются, так как потенциалы этих узлов известны.

3. Определим узловые и межузловые проводимости:

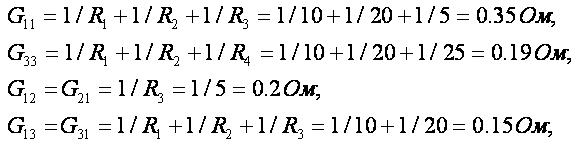
Взаимная проводимость между узлами 2 и 3 равна нулю, так как эти узлы непосредственно не связаны между собой какими-либо ветвями» т.е. G23 = G32 = 0. Проводимость ветви с источником тока J также равна нулю, так как его внутреннее сопротивление бесконечно велико. Если в какой-либо ветви последовательно включено несколько резисторов, вначале определяется общее сопротивление этой ветви, а затем ее проводимость.

Определим узловые токи:

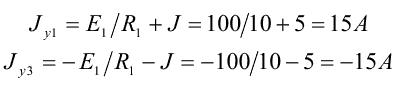
4. Подставим полученные значения узловых и межузловых проводимостей, а также узловых токов в расчетную систему уравнений. Решая ее, определим искомые потенциалы узлов цепи:

Решить систему уравнений можно методом определителей или с помощью микрокалькулятора по соответствующей программе, однако, если система содержит два уравнения, ее целесообразно решать домножением на общие множители:

Запись выше несколько непонятна. Она означает домножение левой и правой частей уравнения на множители. Вообще необходимо любым способом решить систему уравнений: например, подстановкой.

Для проверки расчета целесообразно полученные значения потенциалов, вычисленные с точностью до 3-4 значащей цифры, подставить в исходную систему уравнений, которые при этом, очевидно, должны обратиться в тождества.

5. Используя закон Ома, определим токи в ветвях цепи.

Направления токов в ветвях выбраны произвольно и указаны на схеме (рис. I).
Составим выражение для разности потенциалов (напряжения) между узлами 3 и 1:

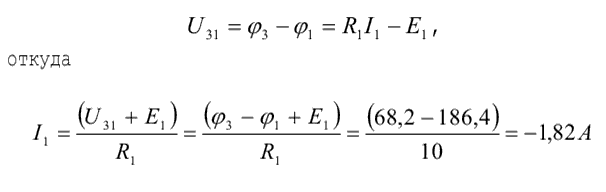
т.е. в дальнейшем при выбранном направлении тока в ветви его величина определяется следующим образом: в числителе выражения от потенциала узла, из которого ток вытекает, вычитается потенциал узла, к которому ток подтекает.

Если в ветви есть ЭДС, она учитывается со знаком «+» («-«), когда ее направление совпадает (противоположно) с направлением тока, В знаменателе выражения для тока находится суммарное сопротивление ветви. Аналогично определяются токи остальных ветвей:

Ток в ветви с идеальной ЭДС Е6 определяется из уравнения, составленного по первому закону Кирхгофа. Например, для узла 2

6. Проверка расчета цепи выполняется по законам Кирхгофа и уравнению энергетического баланса (балансу мощностей), по первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю. Проверяем выполнение этого закона для всех узлов цепи (кроме узла 2: из уравнения для этого узла определялся ток I6:

По второму закону Кирхгофа алгебраическая сумма ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на элементах этого контура. Проверяем выполнение этого закона дня всех независимых контуров заданной цепи;
Для контура с элементами Е1, R1 и R2

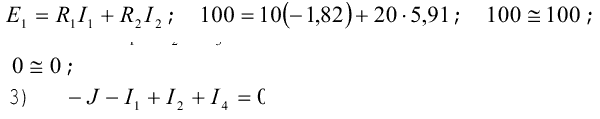
для контура с элементами R2, R3, R4 и R5

для контура с элементами E1, R3, E6, R4 и R1

Дня любой электрической цепи мощность, потребляемая резисторами этой цепи, должна равняться мощности источников энергии. Уравнение энергетического баланса ( баланс мощностей) в общем виде записывается следующим образом:

В левой части уравнения учтена мощность источников энергии. Мощность источников ЭДС учитывается с положительным (отрицательным) знаком, если ток, протекающий через источник ЭДС, совпадает ( противоположен) с направлением ЭДС.

Для определения знака мощности источника тока необходимо определить напряжение на источнике. Если ток источника вытекает из точки с меньшим потенциалом и подтекает к точке с большим потенциалом, мощность источника будет положительной (источник генерирует энергию).

Если ток источника вытекает из точки более высокого потенциала по сравнению с потенциалом точки, куда ток втекает, мощность источника будет отрицательной, а режим его работы соответствует потреблению энергии.

В правой части уравнения энергетического баланса записывается арифметическая сумма мощностей, потребляемых резисторами цепи и определяемых по закону Джоуля-Ленца. По своему физическому смыслу эти мощности могут быть только положительными.
Для заданной электрической цепи (рис. I) уравнение энергетического баланса имеет вид

Расчет считается выполненным правильно, если расхождение между левой и правой частями уравнения электрического баланса не превышает 1. 2%. Следует помнить, что при выполнении проверки расчета по законам Кирхгофа и балансу мощностей уравнения составляются по выбранным. В начале расчета положительным направлениям токов в ветвях заданной цепи, а числовые значения токов в уравнения подставляются со знаками, полученными в расчете.

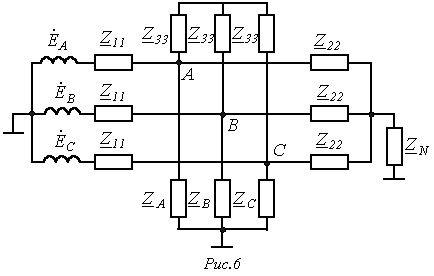
10. В тех случаях, когда трехфазная цепь в целом симметрична, а несимметрия носит локальный характер (местное короткое замыкание или обрыв фазы, подключение несимметричной нагрузки), для расчета удобно применять теорему об активном двухполюснике.

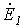
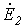
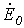
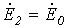
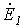
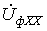
При мысленном устранении несимметрии (несимметричного участка) для оставшейся цепи имеет место симметричный режим холостого хода. В соответствии с методом эквивалентного генератора теперь необходимо определить эквивалентные ЭДС и входные сопротивления симметричной цепи. В общем случае – при несимметрии в системе фазных напряжений источника – помимо эквивалентной ЭДС прямой последовательности будут также иметь место эквивалентные ЭДС обратной и нулевой последовательностей. Однако обычно напряжения генераторов симметричны – тогда . Величина , соответствующая напряжению холостого хода на зажимах подключения локальной несимметрии, определяется при отключении локальной несимметричной нагрузки любым известным методом расчета линейных цепей, причем в силу симметрии цепи расчет проводится для одной фазы.

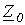
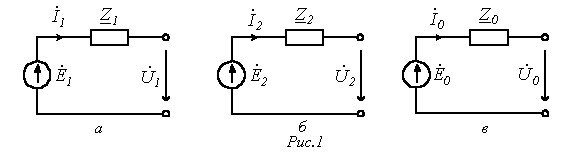
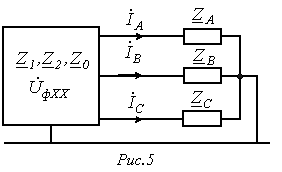
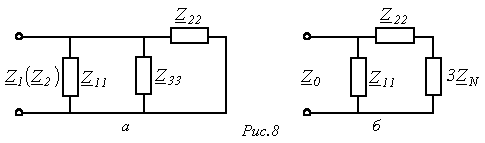
В отдельности рассчитываются входные сопротивления симметричной цепи для различных последовательностей, которая предварительно преобразуется известными методами в пассивную цепь. При этом при расчете входного сопротивления нулевой последовательности необходимо учитывать только те участки цепи, которые соединены с нейтральным проводом или заземленной нейтральной точкой, т.е. принимать во внимание только те ветви, по которым могут протекать токи нулевой последовательности. Схемы для расчета входных сопротивлений прямой и обратной последовательностей одинаковы, однако в случае вращающихся машин величины этих сопротивлений различны.

Поскольку в отдельности для каждой симметричной последовательности имеет место симметричный режим, расчет указанным методом ведется на одну фазу с использованием расчетных схем для прямой (рис. 1,а), обратной (рис. 1,б) и нулевой (рис. 1,в) последовательностей.

Данным схемам соответствуют соотношения

;

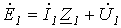(1)

;

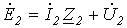(2)

.

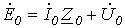(3)

Поскольку соотношений три, а число входящих в них неизвестных шесть 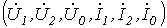, необходимо составление трех дополнительных уравнений, учитывающих конкретный вид несимметрии.

Рассмотрим некоторые типовые примеры применения метода.

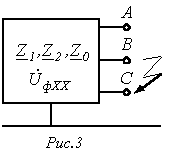
Однополюсное короткое замыкание на землю (рис. 2).

.

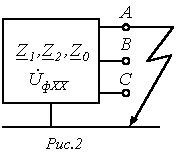
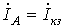
Поскольку фаза А замкнута на землю, то дополнительные уравнения имеют вид

;

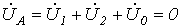(4)

;

.

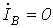
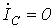
С учетом последних соотношений уравнения (1)…(3) можно записать в виде

;

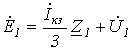(5)

;

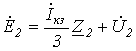(6)

.

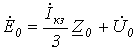(7)

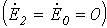
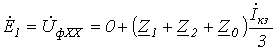
Принимая во внимание (4), а также то, что источник питания симметричный , просуммируем (5), (6) и (7):

,

Двухполюсное короткое замыкание без земли (рис. 3).

Для рассматриваемого случая можно записать

Последнее равенство объясняется отсутствием пути для протекания токов нулевой последовательности.

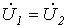
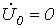
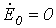
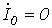
Из двух последних соотношений вытекает, что . При этом , так как и .

Подставив полученные выражения для напряжений и токов прямой и обратной последовательностей в (1) и (2), запишем

;

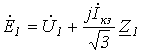(8)

.

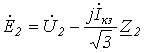(9)

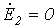
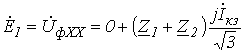
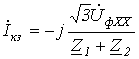
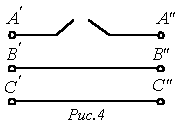
Вычитая из (8) соотношение (9) и учитывая, что в силу симметрии источника , получим

,

.

Обрыв линейного провода (рис. 4) – определить напряжение в месте разрыва.

В рассматриваемом случае дополнительные уравнения имеют вид:

;

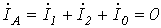(10)

;

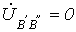(11)

.

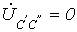(12)

Из соотношений (11) и (12) вытекает равенство:

.

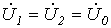(13)

На основании (1)…(3) с учетом (13) запишем

.

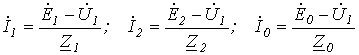
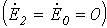
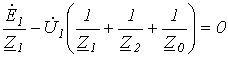
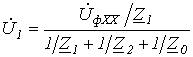
Принимая во внимание симметричность источника , подставим последние выражения в (10):

,

.

Таким образом, искомое напряжение

.

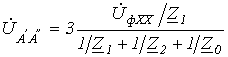
Подключение несимметричной нагрузки 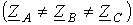к симметричной цепи (рис. 5).

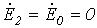
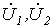
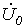
Учитывая, что , подставим в уравнения (1)…(3) определенные в предыдущей лекции выражения и (см. соотношение (12) в лекции №19):

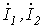
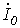
Решая данную систему уравнений, находим и . Тогда

и .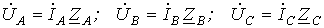

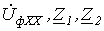
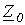
В рассмотренных примерах предполагалось, что необходимые для анализа цепи параметры и предварительно определены. Рассмотрим их расчет на примере предыдущей задачи для некоторой схемы на рис. 6.

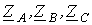
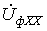
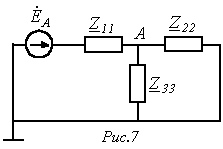
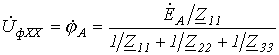
Поскольку при отключении несимметричной нагрузки оставшаяся часть схемы будет работать в симметричном режиме, для определения получаем расчетную однофазную схему на рис. 7.

Из нее

.

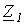
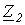
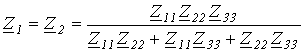
Схема для определения входных сопротивлений прямой и обратной последовательностей одна и та же и соответствует цепи на рис. 8,а. В соответствии с ней

.

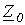
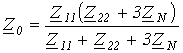
Схема для определения , полученная с учетом возможных путей протекания токов нулевой последовательности, приведена на рис. 8,б. Из нее

.

Передача энергии от активного двухполюсника к пассивному

Прежде всего установим соотношение между сопротивлениями rвх и r, при выполнении которого мощность пассивного двухполюсника максимальна.

Мощность пассивного двухполюсника определяется выражениями

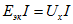
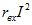
где -мощность, развиваемая эквивалентным активным двухполюсником; -мощность потерь в этом двухполюснике (в сопротивлении rвх).

Для определения тока I, при котором мощность Р максимальна, найдем производную от Р по I из уравнения (2.22) и приравняем ее нулю:

откуда искомый ток 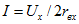[уравнением (2.23) пользоваться нельзя, так как его правая часть содержит две переменные: r и I].
В общем случае (рис. 2.14, д) ток 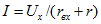. Значит, мощность максимальна при

т. е. при равенстве входных сопротивлений пассивного и активного двухполюсников.
По (2.23) при r = rв мощность

Отношение мощности Р пассивного двухполюсника к мощности 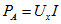, развиваемой эквивалентным активным двухполюсником, называется КПД эквивалентного активного двухполюсника:

Смотри ещё по разделу на websor:

— Принцип наложения (суперпозиции);

— Входные и взаимные проводимости, коэффициенты передачи;

— Принцип компенсации. Зависимые источники;

— Общие замечания о двухполюсниках и многополюсниках;

— Линейные соотношения между напряжениями и токами;

— Теорема о взаимных приращениях токов и напряжений;

— Принцип эквивалентного генератора;

— Передача энергии от активного двухполюсника к пассивному.

Из (2.25) следует, что при максимальной мощности пассивного двухполюсника КПД равен 0,5. Более высокие значения КПД будут при .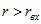

КПД реального активного двухполюсника равен КПД эквивалентного только при выполнении определенного условия. Если при отключении пассивного двухполюсника от реального активного в ветвях последнего не будет токов и потерь, так же как и в эквивалентной схеме на рис. 2.14,д, то КПД реального и эквивалентного активных двухполюсников равны. При невыполнении этого условия КПД реального активного двухполюсника меньше КПД эквивалентного двухполюсника.

Мощность, развиваемая источником,

напряжение на выводах приемника

В случае передачи по линии электрической энергии при большой мощности стремятся получить возможно больший КПД, для чего необходимо, как непосредственно следует из (2.26), иметь 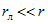. При передаче сигналов по линии связи стремятся получить максимальную мощность в приемнике, что приводит к низкому значению КПД.
Первые опыты передачи электрической энергии при постоянном токе осуществил русский инженер Ф. А. Пироцкий. В 1874 г. вблизи г. Петербурга Ф. А. Пироцкий создал линию передачи энергии при мощности около 6 л. с. на расстояние до 1 км. Затем он проводил опыты передачи электрической энергии по рельсам конно-железной дороги.

На основании своих опытов Ф. А. Пироцкий установил, что можно передавать электрическую энергию при большой мощности на большие расстояния. В качестве источников энергии для первичных двигателей он предложил пользоваться энергией водных потоков. Теоретические основы передачи электрической энергии по линии разработал Д. А. Лачинов. В 1880 г. он опубликовал в первом номере журнала «Электричество» свой труд «Электромеханическая работа».

Источник