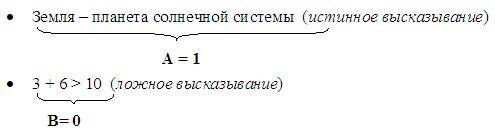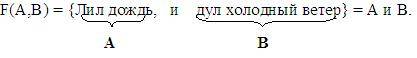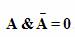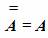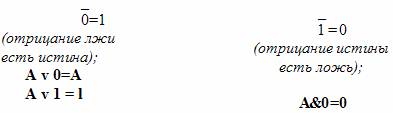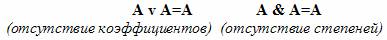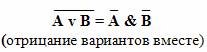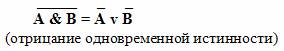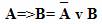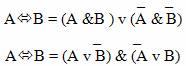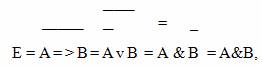Чем заменяются высказывания в алгебре высказываний

Алгебра высказываний

Алгебра высказываний

Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.)

Логическая переменная – это простое высказывание.
Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.

Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Например,

Многие люди не любят сырую погоду.

Пусть А = «Многие люди любят сырую погоду». Получаем логическую функцию F(A) = не А.

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).

Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.

Пример:
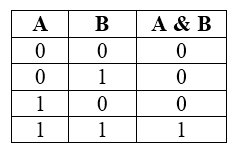
Рассмотрим составное высказывание «2 • 2 = 4 и 3 • 3 = 10». Выделим простые высказывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «3 • 3 = 10» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A /\ B = 1 /\ 0 = 0 (в соответствии с таблицей истинности), то есть данное составное высказывание ложное.

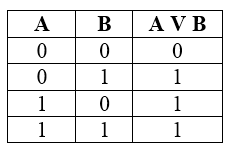
2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;
• в языках программирования — Or.
• Обозначение: \/, +, или, or.
• В алгебре множеств дизъюнкции соответствует операция объединения множеств.

Пример:
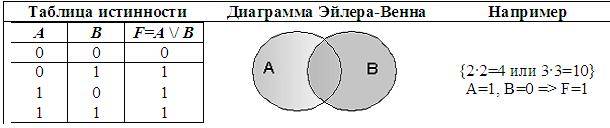
Рассмотрим составное высказывание «2 • 2 = 4 или 2 • 2 = 5». Выделим простые выска-зывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «2 • 2 = 5» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A \/ B = 1 \/ 0 = 1 (в соответствии с таблицей истинности), то есть данное составное высказывание истинно.

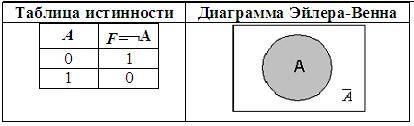
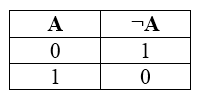
3. Отрицание (инверсия), от лат. InVersion – переворачиваю:

• Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;
• в языках программирования — Not;
• Обозначение: не А, ¬А, not
• В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.

Источник

АЛГЕБРА ВЫСКАЗЫВАНИЙ

АЛГЕБРА ВЫСКАЗЫВАНИЙ является составной частью одного из современных быстро развивающихся разделов математики – математической логики. Математическая логика применяется в информатике, позволяет моделировать простейшие мыслительные процессы. Одним из занимательных приложений алгебры высказываний – решение логических задач.

Объекты алгебры высказываний. Операции над высказываниями. Таблицы истинности.

Алгебра – это наука, которая изучает множество некоторых элементов и действия (операции) над ними. Если элементы алгебры – натуральные числа, а операции – сложение и умножение, то это алгебра натуральных чисел. Действия с направленными отрезками (векторами) изучает векторная алгебра.

Объектами алгебры высказываний являются высказывания. Высказывание – это истинное или ложное повествовательное предложение. Повествовательное предложение, в котором говорится об одном-единственном событии, называется простым высказыванием. Например, предложение «Луна – спутник Земли» есть простое высказывание, предложение «Не сорить!» не является высказыванием.

Высказывания обозначаются большими буквами латинского алфавита. Если высказывание A истинно, то пишут A = 1, если ложно, то используют запись A = 0.

Таблица 1

А	В	АВ
1	1	1
1	0	0
0	1	0
0	0	0

Объединение двух высказываний в одно с помощью союза «ИЛИ», употребляемого в неисключающем смысле, называется операцией логического сложения. Например, высказывание A – «Декабрь – зимний месяц», В – «Летом иногда идет дождь», определим высказывание A+B – «Декабрь – зимний месяц или летом иногда идет дождь». Установить истинность логической суммы можно с помощью следующей таблицы:

Таблица 2

А	В	А+В
1	1	1
1	0	1
0	1	1
0	0	0

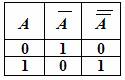
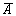
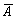
Операция логического отрицания осуществляется над одним высказыванием. Выполнить операцию логического отрицания (обозначается ) – значит получить из данного высказывания новое, присоединяя слова «неверно, что …» ко всему высказыванию. Истинность высказывания определяется таблицей:

Таблица 3

А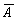
1	0
0	1

Пользуясь определенными выше операциями, можно из простых высказываний образовывать сложные. Например, всевозможные значения для высказывания 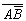можно записать в виде таблицы

Таблица 4

А	B		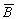A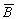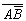
1	1	0	0	1
1	0	1	1	0
0	1	0	0	1
0	0	1	0	1

Тождественные высказывания. Эквивалентные высказывания. Формулы Августа де Моргана.

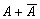
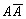
Среди высказываний особое место занимают те, в таблице истинности которых либо одни единицы, либо только нули. Это означает, что высказывание либо всегда истинно, либо ложно, независимо от истинности входящих в него высказываний. Например, высказывание всегда истинно, а высказывание всегда ложно. Доказать это можно составив таблицу истинности этих высказываний.

Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными.

Тождественно истинные или тождественно ложные высказывания, если они встречаются в формулах, заменяются в них, соответственно единицей или нулем:

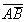
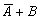
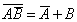
Среди высказываний встречаются такие, таблицы истинности которых совпадают. Эти высказывания называются эквивалентными. Эквивалентными являются, например, высказывания и (то есть ). Это можно проверить составив таблицы истинности этих высказываний:

Источник

Чем заменяются высказывания в алгебре высказываний

Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

1. Логические выражения и логические операции

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).

Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.

Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.

Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.

С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.

Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.

В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.

Существуют разные варианты обозначения истинности и ложности логических переменных:

Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Введем перечисленные логические операции.

В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Источник

Алгебра высказываний

Вы будете перенаправлены на Автор24

Основоположником формальной логики стал древнегреческий философ Аристотель. Формальная логика отвлекается от конкретного содержания высказываний и изучает общие правила построения выводов из преподнесенной информации, которая считается истинной или ложной. Формальная логика изучает высказывания со стороны их истинности или ложности.

Высказывание – это повествовательное предложение, про которое можно однозначно сказать, что оно истинно или ложно.

Побудительные, вопросительные и восклицательные предложения не являются высказываниями.

Используя определение высказывания, определим, можно ли считать высказываниями следующие предложения:

Готовые работы на аналогичную тему

В формальной логике высказывание может быть ложно или истинно, третьего варианта исключено. Обозначим истинное значение за единицу, а ложное за нуль, то получим, что формальная логика представляет собой правила выполнения операций с двоичными кодами (нулями и единицами). Тогда обработка информации сводится к выполнению логических операций над нулями и единицами. Важный шаг в этом направлении сделал английский математик Джордж Буль. Дж.Буль предложил применять для исследования логических высказываний на их истинность или ложность математический механизм. Позже этот раздел математики стали называть алгеброй логики или булевой алгеброй.

Рисунок 1. Дж. Буль (1815‐1864)

Высказывания бывают простые и сложные (составные). Простые высказывания невозможно разделить на более мелкие высказывания, например: «Утро теплое» или «Форточка закрыта». Сложные (составные) высказывания строятся из простых высказываний с помощью логических связок или операций: «И», «ИЛИ», «НЕ», «если…, то», «тогда и только тогда».

Отрицание всегда ставится к действию.

тогда и только тогда: «Утро теплое тогда и только тогда, когда форточка закрыта».

Операции «НЕ», «И» и «ИЛИ» используются чаще других. С помощью этих операций можно описать любое действие, поэтому они называются основными или базовыми операциями.

Таблица истинности для отрицания:

В таблице истинности будет два столбца с исходными значениями.

В алгебре логики доказано, что операций «НЕ», «И» и «ИЛИ» достаточно для того, чтобы записать с их помощью любую другую логическую операцию, которую только можно придумать. Операций «НЕ», «И» и «ИЛИ» являются базисом или базовыми операциями.

Эквивалентность (также равносильность, эквиваленция) – это логическая операция, соответствующая связке «тогда и только тогда» или «необходимо и достаточно».

Источник

Основы алгебры логики

Основные законы алгебры логики.

Законы алгебры высказываний

Алгебра высказываний (алгебра логики) — раздел математической логики, изучающий логические операции над высказываниями и правила преобразования сложных высказываний.

При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы.

Законы алгебры высказываний (алгебры логики) — это тавтологии.

Иногда эти законы называются теоремами.

В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул. Среди законов особо выделяются такие, которые содержат одну переменную.

Первые четыре из приведенных ниже законов являются основными законами алгебры высказываний.

Закон тождества:

Всякое понятие и суждение тождественно самому себе.

Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки.

Например, рассуждение Правильно говорят, что язык до Киева доведет, а я купил вчера копченый язык, значит, теперь смело могу идти в Киев неверно, так как первое и второе слова «язык» обозначают разные понятия.

В рассуждении: Движение вечно. Хождение в школу — движение. Следовательно, хождение в школу вечно слово «движение» используется в двух разных смыслах (первое — в философском смысле — как атрибут материи, второе — в обыденном смысле — как действие по перемещению в пространстве), что приводит к ложному выводу.

Закон непротиворечия :

В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А. Примеры выполнения закона исключенного третьего:

1. Число 12345 либо четное, либо нечетное, третьего не дано.

2. Предприятие работает убыточно или безубыточно.

3. Эта жидкость является или не является кислотой.

Закон исключенного третьего не является законом, признаваемым всеми логиками в качестве универсального закона логики. Этот закон применяется там, где познание имеет дело с жесткой ситуацией: « либо — либо », « истина—ложь ». Там же, где встречается неопределенность (например, в рассуждениях о будущем), закон исключенного третьего часто не может быть применен.

Рассмотрим следующее высказывание: Это предложение ложно. Оно не может быть истинным, потому что в нем утверждается, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.

Парадокс (греч. paradoxos — неожиданный, странный) в этом примере возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере: В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру? В логике из-за ее формальности нет возможности получить форму такого ссылающегося самого на себя высказывания. Это еще раз подтверждает мысль о том, что с помощью алгебры логики нельзя выразить все возможные мысли и доводы. Покажем, как на основании определения эквивалентности высказываний могут быть получены остальные законы алгебры высказываний.

По определению равносильности мы должны найти тот столбец, значения которого совпадают со значениями столбца А. Таким будет столбец А.

Таким образом, мы можем сформулировать закон двойного отрицания:

Аналогичным образом можно вывести и проверить следующие законы:

Свойства констант:

Законы идемпотентности:

Законы коммутативности:

Операнды А и В в операциях дизъюнкции и конъюнкции можно менять местами.

Законы ассоциативности:

A v(B v C) = (A v B) v C;

Если в выражении используется только операция дизъюнкции или только операция конъюнкции, то можно пренебрегать скобками или произвольно их расставлять.

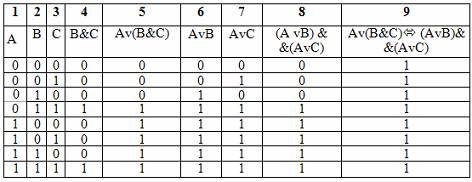
Законы дистрибутивности:

A v (B & C) = (A v B) &(A v C)

(дистрибутивность дизъюнкции
относительно конъюнкции)

А & (B v C) = (A & B) v (А & C)

(дистрибутивность конъюнкции
относительно дизъюнкции)

Закон дистрибутивности конъюнкции относительно дизъюнкции ана­логичен дистрибутивному закону в алгебре, а закон дистрибутивности дизъюнкции относительно конъюнкции аналога не имеет, он справедлив только в логике. Поэтому необходимо его доказать. Доказательство удобнее всего провести с помощью таблицы истинности:

Законы поглощения:

Проведите доказательство законов поглощения самостоятельно.

Законы де Моргана:

Словесные формулировки законов де Моргана:

Мнемоническое правило: в левой части тождества операция отрицания стоит над всем высказыванием. В правой части она как бы разрывается и отрицание стоит над каждым из простых высказываний, но одновременно меняется операция: дизъюнкция на конъюнкцию и наоборот.

Примеры выполнения закона де Моргана:

1) Высказывание Неверно, что я знаю арабский или китайский язык тождественно высказыванию Я не знаю арабского языка и не знаю китайского языка.

2) Высказывание Неверно, что я выучил урок и получил по нему двойку тождественно высказыванию Или я не выучил урок, или я не получил по нему двойку.

Замена операций импликации и эквивалентности

Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.

Так, заменить операцию импликации можно в соответствии со следующим правилом:

Для замены операции эквивалентности существует два правила:

В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.

Знание правил замены операций импликации и эквивалентности помогает, например, правильно построить отрицание импликации.

Рассмотрим следующий пример.

Пусть дано высказывание:

Источник