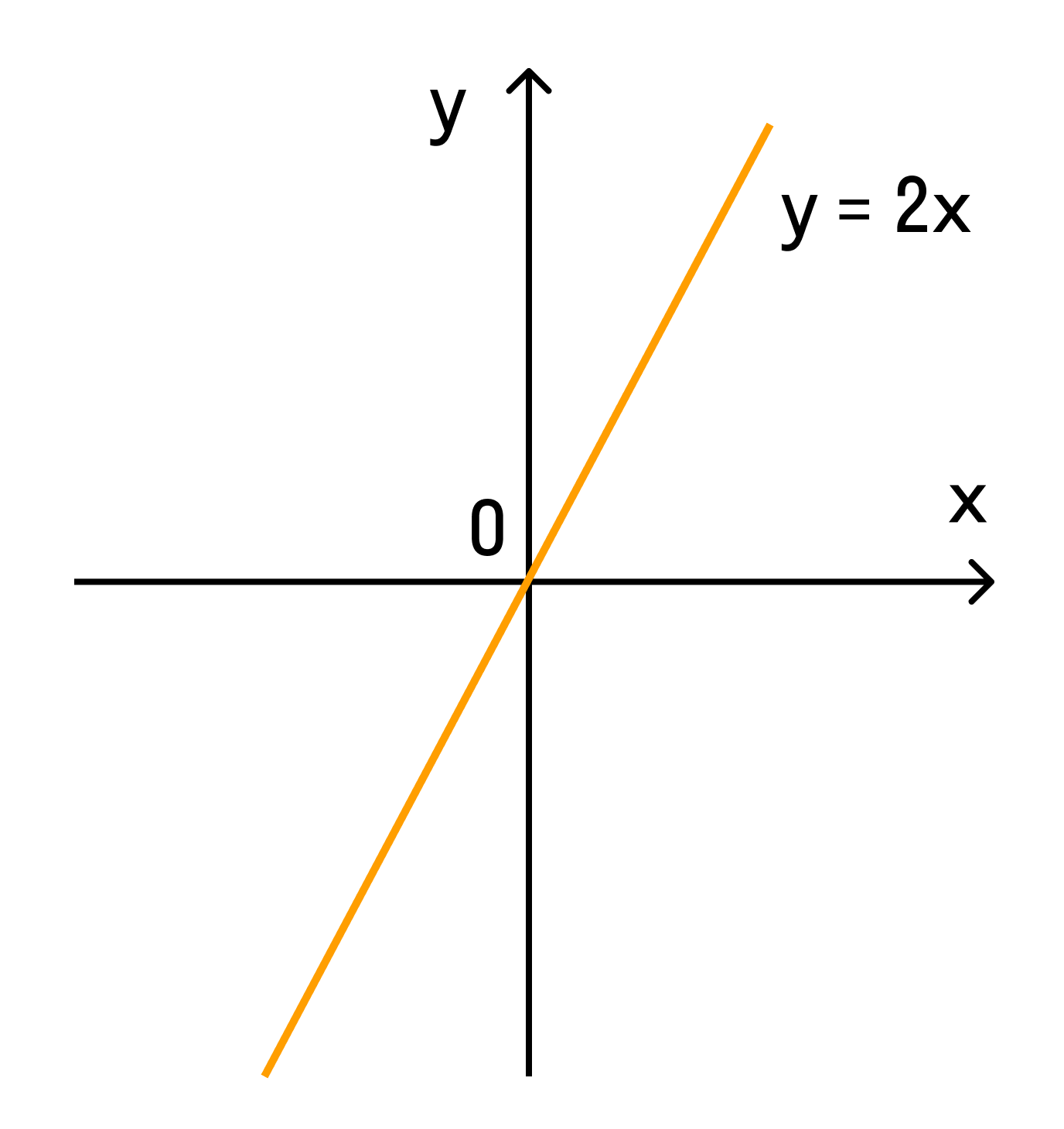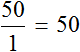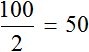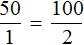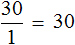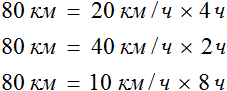Формула чем больше тем меньше

Прямая и обратная пропорциональность

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Зависимости также можно классифицировать по формам: функциональная и статистическая.

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.

В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.

Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Графиком прямо пропорциональной зависимости величин является прямая линия.

Например, при k = 2 график выглядит так:

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

Формула обратной пропорциональности

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

Графиком обратно пропорциональной зависимости величин является гипербола.

Свойства функции обратной пропорциональности:

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Соотношения равны, но перевернуты относительно друг друга.

Источник

Прямая и обратная пропорциональность

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.

Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.

Прямая пропорциональность

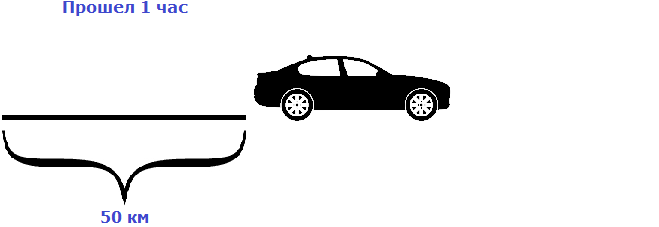
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.

Изобразим на рисунке расстояние, пройденное автомобилем за 1 час

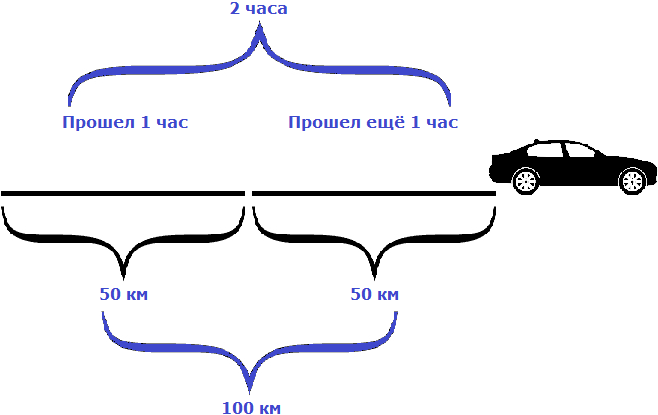
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км

Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.

Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.

Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.

Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.

Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.

В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.

Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50

Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.

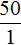
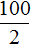
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:

Это отношение можно прочитать следующим образом:

Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.

Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.

Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.

Запишем чему равно отношение тридцати рублей к одному килограмму

Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:

Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.

Обратная пропорциональность

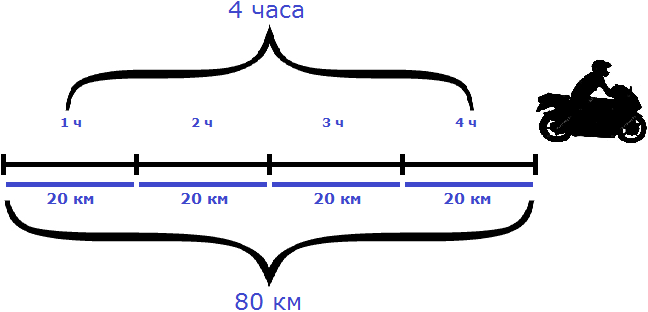
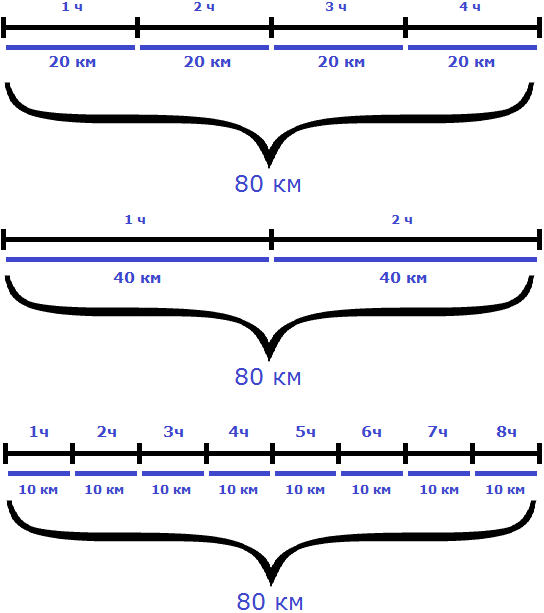
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.

Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:

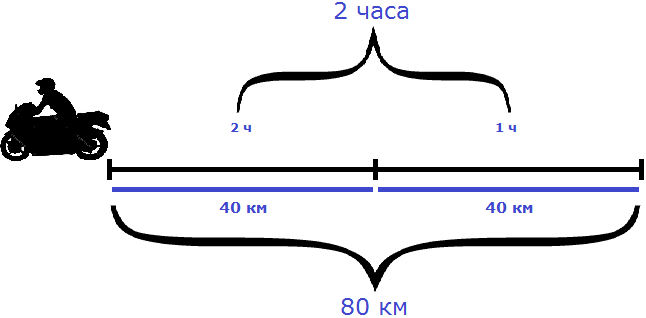
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.

Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.

Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.

Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.

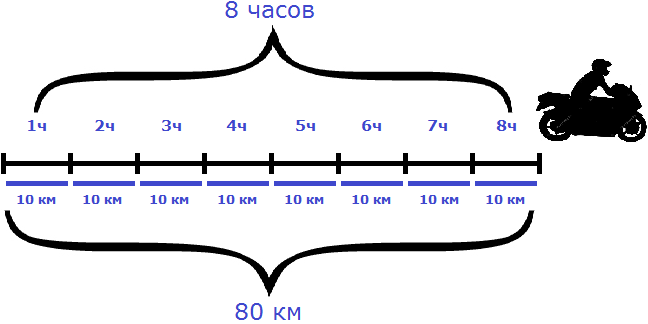
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:

Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.

Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.

В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным

Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

10 thoughts on “Прямая и обратная пропорциональность”

что ценно теория методически верно преподается. очень добрый сайт.

мне теперь всё понятно, большое спасибо сайту

Источник

Урок 23 Бесплатно Прямая и обратная пропорциональные зависимости

На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.

Прямая и обратная пропорциональность

Давайте сначала разберемся, что такое пропорциональность.

Зависимость величин друг от друга может быть прямой и обратной.

Отношение между величинами описываются прямой или обратной пропорциональностью.

Прямая пропорциональность выражается так: \(\mathbf\)

Обратная пропорциональность выражается так: \(\mathbf>\)

x и y величины, зависящие друг от друга.

Пример

Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.

По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.

Какова эта зависимость, сейчас и рассмотрим.

Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.

Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.

Пусть одна клетка равна 1 см. Рассмотрим рисунок:

Ширина прямоугольника b постоянная величина

b = 4 см

a₁ = 6 см

a₂ = 7 см

Найдем площади прямоугольников S₁ и S₂

\(\mathbf = a_ <1>\cdot b = 6 \cdot 4 = 24>\) см 2

\(\mathbf = a_ <2>\cdot b = 7 \cdot 4 = 28>\) см 2

Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.

Рассмотрим другой вариант зависимости

Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см

Площадь прямоугольника S постоянная величина

S = 24 см 2

b₁ = 4 см

Увеличим высоту прямоугольника- сторону прямоугольника b₁ на 2 см_, получим

b₂ = 6 см

Найдем ширину прямоугольника- сторону a₂

Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.

Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:

1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.

2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.

Примеров прямой и обратной пропорциональности множество.

Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.

Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.

Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается

Пройти тест и получить оценку можно после входа или регистрации

Алгоритм решение задач с прямой и обратной пропорциональной зависимостью

Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:

— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин

— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.

5. Записать пропорцию, учитывая характер пропорциональности величин

6. Составить уравнение

7. Найти неизвестный член уравнения (искомую величину)

8. Записать ответ задачи

Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.

Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.

Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.

Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.

При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Обратная пропорциональность. Гипербола

Сейчас мы будем говорить об обратной пропорциональности, или другими словами об обратной зависимости, как о функции.

Мы закрепим понятие функции и научимся работать с коэффициентами и графиками.

А еще мы разберем несколько примеров построения графика функции — гиперболы.

Обратная пропорциональность — коротко о главном

Определение:

Функция, описывающая обратную пропорциональность, – это функция вида \( \displaystyle y=\frac+b \), где \( k\ne 0\), \( x\ne 0\) и \( x\ne а\)

По-другому эту функцию называют обратной зависимостью.

Область определения и область значений функции:

График обратной пропорциональности (зависимости) – гипербола.

Коэффициент \( \displaystyle k\)

\( \displaystyle k\) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).

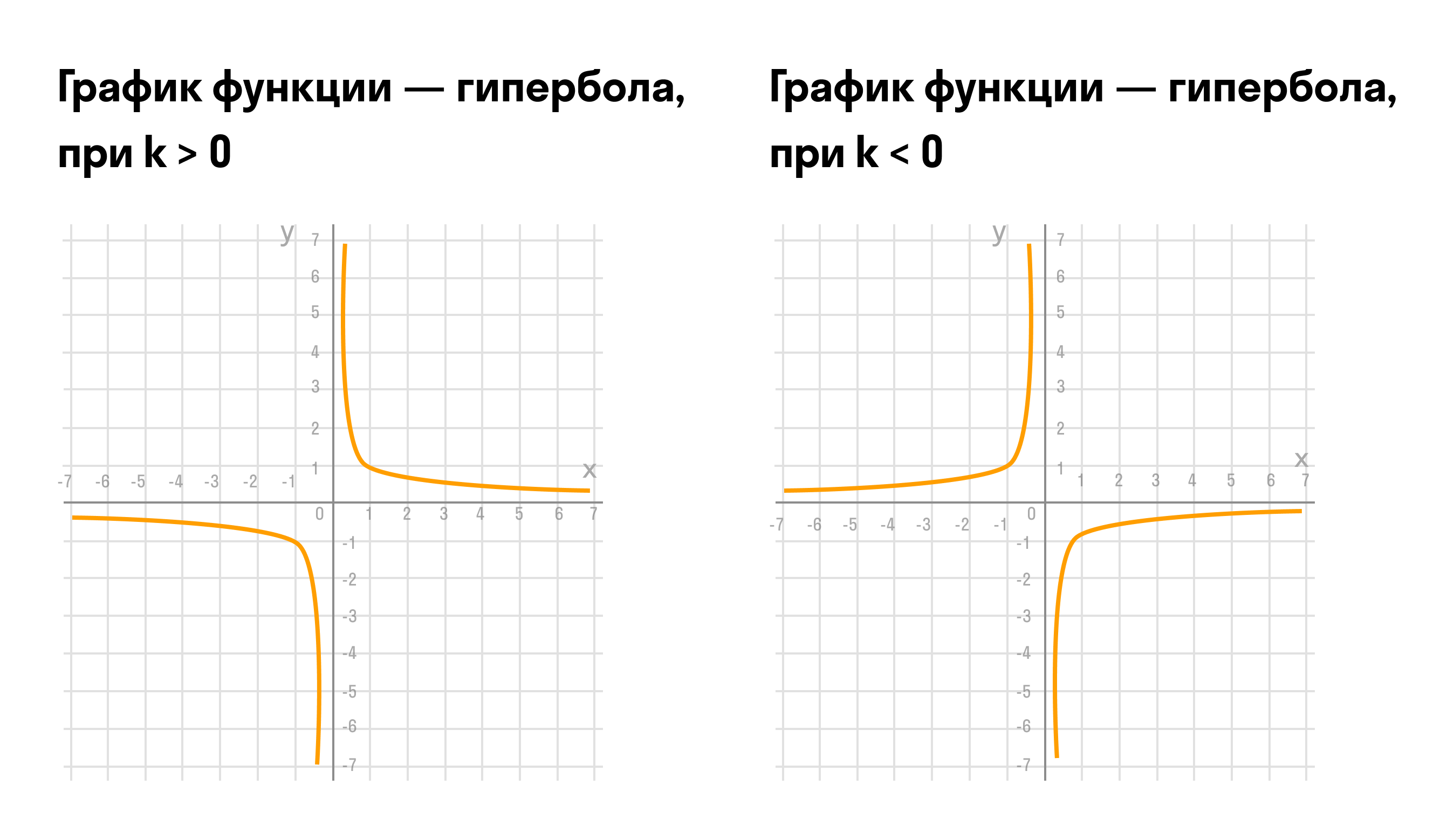
Знак коэффициента \( \displaystyle k\) влияет на то, в каких четвертях расположен график:

если \( \displaystyle k>0\), то ветви гиперболы расположены в \( \displaystyle I\) и \( \displaystyle III\) четвертях;

если \( \displaystyle k

Коэффициент \( \displaystyle a\)

Если внимательно посмотреть на знаменатель, видим, что \( \displaystyle a\) – это такое число, которому не может равняться \( \displaystyle x\).

То есть \( x=a\) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции

Коэффициент \( b\)

Число \( b\) отвечает за смещение графика функции вверх на величину \( b\), если \( b>0\), и смещение вниз, если \( b

Пример 2

Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).

Напомню, что для этого надо найти корни соответствующего квадратного уравнения: \( \displaystyle <^<2>>+4-5=0\).

Я найду их устно с помощью теоремы Виета: \( \displaystyle <_<1>>=-5\), \( \displaystyle <_<2>>=1\). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения».

Итак, получаем: \( \displaystyle <^<2>>+4-5=\left( x+5 \right)\left( x-1 \right)\), следовательно:

Пример 3

Ты уже попробовал решить сам? В чем загвоздка?

Наверняка в том, что в числителе у нас \( \displaystyle 2x\), а в знаменателе – просто \( \displaystyle x\).

Это не беда. Нам нужно будет сократить на \( \displaystyle \left( x+2 \right)\), поэтому в числителе следует вынести \( \displaystyle 2\) за скобки (чтобы в скобках \( \displaystyle x\) получился уже без коэффициента):

Ответ: \( \displaystyle y=2-\frac<5>\).

График обратной пропорциональности

Как всегда, начнем с самого простого случая: \( \displaystyle y=\frac<1>\).

Таблица обратной пропорциональности (зависимости)

Нарисуем точки на координатной плоскости:

Теперь их надо плавно соединить, но как?

Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.

Это график гиперболы и выглядит он так:

Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.

Каждая из них стремится своими концами приблизиться к осям \( \displaystyle Ox\) и \( \displaystyle Oy\), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:

Оно и понятно: так как \( \displaystyle x\ne 0\), график не может пересекать ось \( \displaystyle Oy\). Но и \( \displaystyle y\ne 0\), так что график никогда не коснется и оси \( \displaystyle Ox\).

Ну что же, теперь посмотрим на что влияют коэффициенты.

На что влияют коэффициенты

Рассмотрим такие функции:

Ух ты, какая красота!

Все графики построены разными цветами, чтобы легче было их друг от друга отличать.

Итак, на что обратим внимание в первую очередь?

Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси \( \displaystyle Ox\).

Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.

А что, если функция выглядит сложнее, например, \( \displaystyle y=\frac<1>+2\)?

В этом случае гипербола будет точно такой же, как обычная \( \displaystyle y=\frac<1>\), только она немного сместится. Давай думать, куда?

Чему теперь не может быть равен \( x\)? Правильно, \( x\ne 1\). Значит, график никогда не достигнет прямой \( x=1\).

А чему не может быть равен \( y\)? Теперь \( y\ne 2\). Значит, теперь график будет стремиться к прямой \( y=2\), но никогда ее не пересечет.

Итак, теперь прямые \( x=1\) и \( y=2\) выполняют ту же роль, которую выполняют координатные оси для функции \( \displaystyle y=\frac<1>\).

Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):

Более подробно о том, как строятся такие графики, мы выучим чуть позже.

А теперь попробуй решить несколько примеров для закрепления.

Примеры

1. На рисунке изображен график функции \( \displaystyle y=\frac\). Определите \( k\).

2. На рисунке изображен график функции \( \displaystyle y=\frac\). Определите \( k\)

3. На рисунке изображен график функции \( \displaystyle y=\frac<1>\). Определите \( a\).

4. На рисунке изображен график функции \( \displaystyle y=\frac<1>+a\). Определите \( a\).

5. На рисунке приведены графики функций \( \displaystyle y=\frac,\text< >y=\frac\) и \( y=\frac\).

Источник