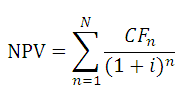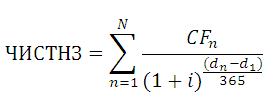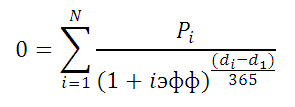Формула всд в excel что показывает
Функция ВСД для расчета внутренней ставки доходности в Excel
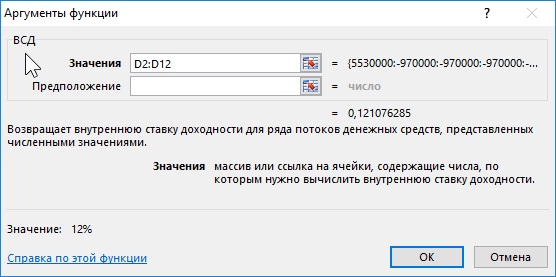
Функция ВСД в Excel используется для расчета внутренней ставки доходности на основе имеющихся числовых данных о финансовых потоках, принимаемых в качестве первого аргумента, и возвращает соответствующее приближенное значение.
Примеры использования функции ВСД в Excel
В отличие от аннуитетной схемы, при которой выплаты должны иметь фиксированную неизменяемую во времени сумму, при расчете внутренней ставки доходности допускаются колебания размеров сумм финансовых поступлений. Для корректных расчетов поступления должны являться регулярными, то есть выполняться через определенные промежутки времени (периоды), например, раз в месяц или раз в квартал.
Внутренняя ставка доходности представляет собой такое значение процентной ставки, при которой стоимость всех финансовых потоков будет равна 0 (нулю), то есть инвестор сможет возместить свои убытки, связанные с финансированием инвестиционного проекта, но без получения какой-либо прибыли.
Сравнительный анализ кредитов по условиям кредитования в Excel
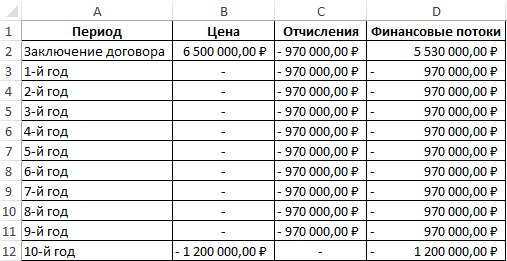
Пример 1. Строительной компании требуется автокран стоимостью 6,5 млн рублей. Стоимость аренды автокрана у другой компании составляет 560000 рублей в год, а срок полезного использования составляет 10 лет, по истечению которых остаточная стоимость автокрана составит всего 1200000 рублей, а он возвращается в собственность арендодателю. Альтернативным вариантом является привлечение стороннего капитала со ставкой 19% годовых. Какой вариант более выгодный?
Вид таблицы данных:
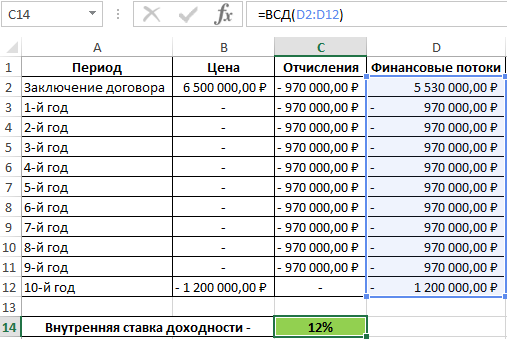
Для расчета внутренней ставки доходности на основе имеющихся данных используем формулу:
Ячейки из диапазона D2:D12 содержат числовые значения финансовых потоков на протяжении 10 лет аренды автокрана. В результате расчетов получим:
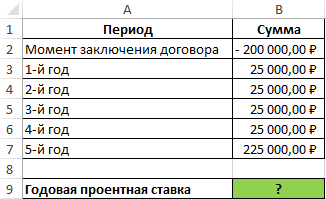
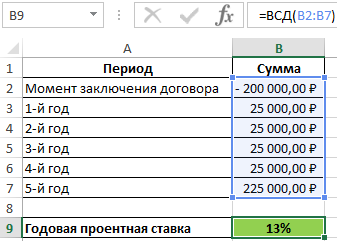
Такой результат свидетельствует о том, что аренда автокрана выгоднее, чем привлечение внешних инвестиций на его приобретение (например, кредит в банке), так как 12% Пример 2. Клиент открыл депозитный счет в банке на 5 лет и перевел средства на сумму 200000 рублей. Ежегодно он снимал по 25000 рублей процентов, а в последний год вывел со счета вложенную сумму и последние начисленные проценты. Определить годовую процентную ставку по депозиту.
Вид таблицы данных:
Начальная сумма указана в виде отрицательного числа, поскольку для клиента операция по внесению средств на депозитный счет является расходной. Процентная ставка по депозиту эквивалентна внутренней ставки доходности, поскольку депозит в банк можно рассматривать в качестве инвестиционного проекта. Рассчитаем значение ставки по формуле:
Депозитный счет был открыт под 13% годовых.
Сравнительный анализ инвестиций по условиям вкладов в Excel
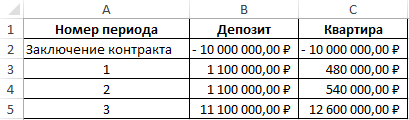
Вид таблицы данных:
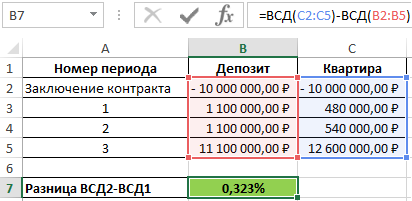
Предположим, что инвестиционный проект по вложению средств на покупку квартиры является более выгодным. Тогда используем следующую формулу для расчета:
Как видно, покупка квартиры и последующая сдача ее в аренду является более прибыльной идеей, однако это предприятие сопряжено с различными рисками и основывается на предположении, что квартиру удастся продать за 12 млн. рублей.
Особенности использования функции ВСД в Excel
Функция имеет следующую форму синтаксической записи:
=ВСД( значения; [предположения])
Пример формулы расчета внутренней ставки доходности в Excel
При вычислении текущей стоимости инвестиций на основе показателей, прогнозируемых будущих регулярных взносов с разными суммами полученное значение, сравнивается с начальной суммой необходимого объема инвестиций. Если текущая стоимость инвестиций больше чем необходимая сумма вложения финансовых средств, значит процент возврата вложенных средств выше чем ожидается. Но в таком случае возникает вопрос: какая же реальная фактическая процентная ставка доходности инвестиций при данных условиях?
Функция ВСД для расчета внутренней ставки доходности IRR проекта в Excel
Для вычисления внутренней ставки нормы доходности будущих вложений Excel предлагает функцию ВСД (Внутренняя Ставка Доходности). Данная функция очень тесно связанна с функцией для вычисления текущей стоимости инвестиций ЧПС. Функция ВСД служит для расчета внутренней ставки доходности в Excel, при которой для тех самых регулярных будущих взносов функция ЧПС буде возвращать свой итоговый результат вычисления равный нулю (0).
Чтобы использовать функцию ВСД необходимо подготовить входные данные. В диапазоне значений должно находится минимум одно отрицательное и одно положительное число суммы будущих платежей. Если же все суммы будут положительными – это будет значит, что ничего не инвестируется, а только возвращается платежами доходности от инвестиций, например, дивиденды, прибыль с выручки и т.п. Это положительный сценарий, но мало вероятный на практике. Обычно платежи инвестирования идут в начале периода реализации инвестиционного проекта, а платежи доходов от инвестиций идут под его конец. Не всегда так бывает, но всегда будет минимум 1 платеж с отрицательным числом (на расход) и минимум 1 платеж с положительным платежом (на приход).
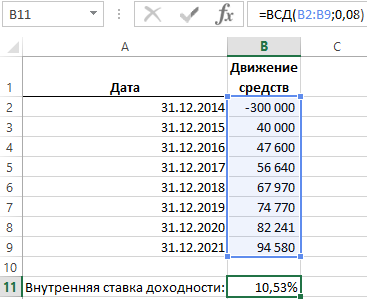
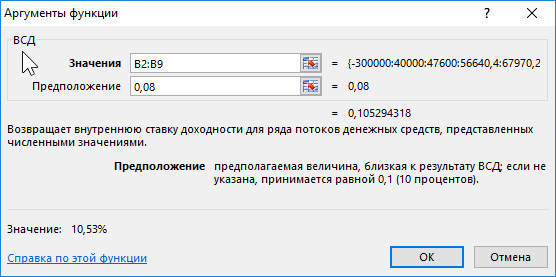
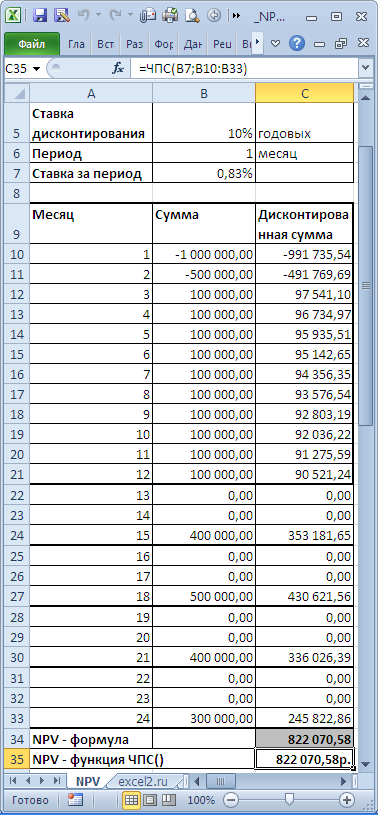
Ниже на рисунке представлен хронологический график дивидендных выплат. В нем учитывается начальная сумма инвестиций для того, чтобы функция ВСД возвращала правильный итоговый результат вычисления. В начале таблицы графика находится строка содержащая значение суммы инвестиционного вложения равной 300 000$. Ниже приведенная формула отображает внутреннюю ставку доходности равной 10,53%:
Первый аргумент функции ВСД содержит диапазон ячеек с платежами на протяжении всего инвестиционного периода:
Во втором аргументе указана внутренняя процентная ставка доходности инвестиций. Если второй аргумент не указан, Excel по умолчанию присевает значение 10%.
Принцип действия функции ВСД основан на вычислениях значений текущей стоимости суммы для каждого платежа при процентной ставке доходности инвестиций. Если в результате вычислений текущая стоимость суммы очередного платежа больше чем >0, функция уменьшает процентную ставку и выполняет то же вычисление еще раз. Excel повторяет эти же операции изменяя размер процентной ставки и суммируя текущие значения пока сумма не будет равна =0. Тогда функция ВСД возвращает в своем итоговом результате вычисления найденную подходящую процентную ставку.
Расчет внутренней ставки доходности с нерегулярными платежами по ЧИСТВНДОХ
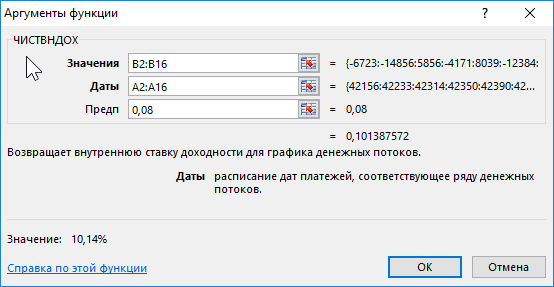
Одинаково как для функции ЧПС так и для функции ВСД принято условия, что все будущие платежи будут регулярными и проведенными в одном и том же промежутке времени. Однако на практике так бывает далеко не всегда. На случай нерегулярных инвестиционных платежей программа Excel предлагает функцию ЧИСТВНДОХ:
В отличии от функции ВСД функция ЧИСТВНДОХ содержит дополнительный обязательный для заполнения аргумент в своем синтаксисе, в которой нужно указать все даты для всех платежей:
Для функции ВСД – даты не нужны, так как обязательным условием считается, что все платежи будут выполнены регулярно и между ними проходит один и тот же период времени. Будит ли это одни день или месяц, или год – для функции ВСД нет никакого значения. Вычисленная процентная ставка с помощью ВСД будет правильной для всех указанных платежей. Это значит, что при ежегодных платежах будет вычисленная процентная ставка доходности – годовых. Если же платежи выполняются ежеквартально – будет получена ставка в ежеквартальной процентной ставке внутренней нормы доходности.
Примечание. Функция ЧИСТВНДОХ имеет родственную функцию ЧИСТНЗ для вычисления текущей стоимости инвестиций при нерегулярных платежах. Данная функция также требует указать даты нерегулярных платежей.
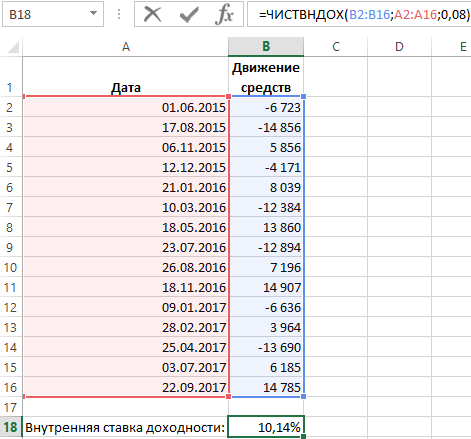
Ниже на рисунке представлен хронологический график с нерегулярными платежами инвестиционных взносов и дивидендных выплат. Иногда инвестор меняет свою инвестиционную стратегию и делает дополнительные вложения на протяжении всего периода реализации инвестиционного проекта при различных условиях: непредвиденные убытки или новые возможности. Учитывая все нерегулярные платежи, инвестиция достигает внутреннюю ставку доходности равную 10,14%. Для ее вычисления была использована функция ЧИСТВНДОХ.
Внутренний принцип действия функции ЧИСТВНДОХ практически идентичный с функционированием ВСД. ЧИСТВНДОХ вычисляет текущую стоимость для отдельно каждого платежа и повторяет результат, изменяя внутреннюю ставку доходности пока вычисляемый результат не будет равен нулю. При вычислении текущей стоимости учитывается количество дней между датами актуального платежа и его предыдущего предшественника. В итоговом результате вычисления функцией ЧИСТВНДОХ будет возвращена реальная внутренняя ставка доходности для всех приходных и расходных нерегулярных инвестиционных платежей.
Внутренняя норма доходности на excel
В данной статье мы рассмотрим, что такое внутренняя норма доходности, какой экономический смысл она имеет, как и по какой формуле рассчитать внутреннюю норму доходности, рассмотрим некоторые примеры расчёта, в том числе при помощи формул MS Exel.
Оглавление
Что такое внутренняя норма доходности?
Внутренняя норма доходности (IRR — Internal Rate of Return) — один из основных критериев оценки инвестиционных проектов (доходности единицы вложенного капитала): ставка дисконта, при которой выполняется равенство суммы дисконтированных доходов по проекту (положительного денежного потока) дисконтированной сумме инвестиций (отрицательному денежному потоку, приведенному объему инвестиций), т.е. когда чистая текущая стоимость (NPV) равна нулю.
В финансово-экономической литературе довольно часто можно встретить синонимы внутренней ставки доходности:
Внутренняя норма доходности отражает как отдачу инвестированного капитала в целом, так и отдачу первоначальных инвестиций. IRR – это ставка дисконтирования, которая приравнивает сумму приведенных доходов от инвестиционного проекта к величине инвестиций, т.е. вложения окупаются, но не приносят прибыль.
Таким образом, анализ внутренней нормы доходности (прибыли) отвечает на главный вопрос инвестора: насколько ожидаемый от проекта денежный поток оправдает затраты на инвестиции в этот проект. Поэтому инвестор при оценке проектов осуществляет расчет IRR каждого проекта и сравнивает его с требуемой нормой прибыли (рентабельности), т.е. со стоимостью своего капитала.
Этот расчет обычно ведется методом проб и ошибок, путем последовательного применения к чистому денежному потоку приведенных стоимостей при различных ставках процента. Главное правило: если внутренняя норма доходности меньше требуемой инвестору ставки дохода на вложенный капитал — проект отвергается, если больше — может быть принят.
Формула расчёта внутренней нормы доходности
Внутренняя норма доходности рассчитывается по следующей формуле:
где
NPVIRR (Net Present Value) — чистая текущая стоимость, рассчитанная по ставке IRR;
CFt (Cash Flow) – денежный поток в период времени t;
IC (Invest Capital) – инвестиционные затраты на проект в первоначальном периоде (тоже являются денежным потоком CF0 = IC).
t – период времени.
или же данную формулу можно представить в виде:
Практическое применение внутренней нормы доходности
Внутренняя норма доходности применяется для оценки инвестиционной привлекательности проекта или для сопоставительного анализа с другими проектами. Для этого IRR сравнивают с эффективной ставкой дисконтирования, то есть с требуемым уровнем доходности проекта (r). За такой уровень на практике зачастую используют средневзвешенную стоимость капитала (Weight Average Cost of Capital, WACC).
| Значение IRR | Комментарии |
|---|---|
| IRR>WACC | У инвестиционного проекта внутренняя норма доходности выше чем затраты на собственный и заемный капитал, т.е. данный проект имеет инвестиционную привлекательность |
| IRR | Инвестиционный проект имеет внутреннюю норму доходности ниже чем затраты на капитал, это свидетельствует о нецелесообразности вложения в него |
| IRR=WACC | Внутренняя норма доходность проекта равна средневзвешенной стоимости капитала, т.е. данный проект находится на минимально допустимом уровне доходности, поэтому следует произвести корректировки движения денежных средств и увеличить денежные потоки |
| IRR1>IRR2 | Инвестиционный проект №1 имеет больший потенциал для вложения чем проект №2 |
Следует отметить, что вместо критерия сравнения WACC может быть использована любая другая норма доходности, например, ставка доходности по государственным облигациям, ставка по банковскому депозиту и т.п. Так, если процентная ставка по депозиту составляет 17%, а IRR инвестиционного проекта составляет 22%, то, очевидно, что деньги следует вкладывать в инвестиционный проект, а не размещать на депозит в банк.
Графический метод поиска внутренней ставки доходности
Предположим, что мы собираемся инвестировать 10 тыс. денежных единиц, и у нас есть варианты их инвестирования в 3 проекта каждый из которых, как предполагается, будет формировать определённые денежные потоки на протяжении 5 лет.
| Период, лет | Проект №1 | Проект №2 | Проект №3 |
|---|---|---|---|
| 0 | -10000 | -10000 | -10000 |
| 1 | 1000 | 1000 | 4000 |
| 2 | 4 000 | 1500 | 3000 |
| 3 | 2000 | 3000 | 2000 |
| 4 | 4000 | 4000 | 1000 |
| 5 | 2000 | 3000 | 1000 |
Продисконтируем вышеуказанные денежные потоки по 3-м проектам по разным процентным ставкам (от 0 до 14%) и на основе полученных результатов построим график.
На графике прослеживается чёткая взаимосвязь между ставкой дисконтирования и чистой текущей стоимостью: чем выше ставка дисконтирования, тем ниже дисконтированная стоимость.
Внутренняя норма доходности, как это следует из определения указанного в начале данной статьи, — это тот уровень ставки дисконта, при которой NPV=0. В нашем примере внутренняя норма доходности определяется в точках пересечения кривых с осью Х. В частности, для проекта №1 IRR составляет 8,9%, для проекта №2 IRR=6,6% и для проекта №3 IRR=4,4%.
Расчёт внутренней нормы доходности (IRR) при помощи MS Exel
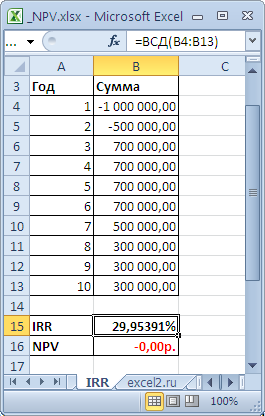
Внутреннюю норму доходности можно довольно легко рассчитать при помощи встроенной финансовой функции ВСД (IRR) в MS Exel.
Функция ВСД возвращает внутреннюю ставку доходности для ряда потоков денежных средств, представленных их численными значениями. Эти денежные потоки не обязательно должны быть равными по величине (как в случае аннуитета), однако они должны иметь место через равные промежутки времени, например ежемесячно или ежегодно. При этом в структуре денежных потоков должен обязательно быть хотя бы один отрицательный денежный поток (первоначальные инвестиции) и один положительный денежный поток (чистый доход от инвестиции).
Также для корректного расчёта внутренней нормы доходности при помощи функции ВСД важен порядок денежных потоков, т.е. если потоки денежных средств отличаются по размеру в разные периоды, то их обязательно необходимо указывать в правильной последовательности.
Синтаксис функции ВСД:
где
Значения — это массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности, учитывая требования указанные выше;
Предположение — это величина, о которой предполагается, что она близка к результату ВСД:
Пример расчёта внутренней ставки доходности (на основе данных о денежных потоках по трём проектам, которые рассматривались выше):
Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в EXCEL
history 3 февраля 2015 г.
Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул MS EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню (взято из Википедии). Или так: Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт cfin. ru) Или так: Текущая стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика . Толковыйсловарь . — М . : « ИНФРА — М «, Издательство « ВесьМир «. Дж . Блэк .)
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма Приведенных стоимостей денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Определившись со сроками денежных потоков, для функции ЧПС() нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см. файл примера, лист NPV ).
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).
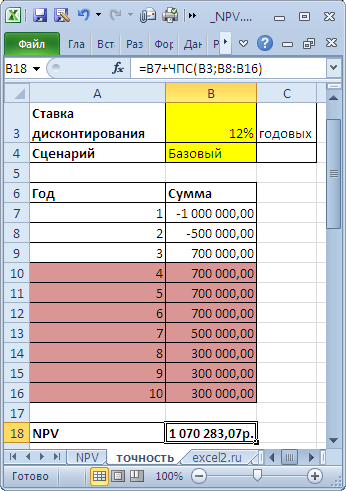
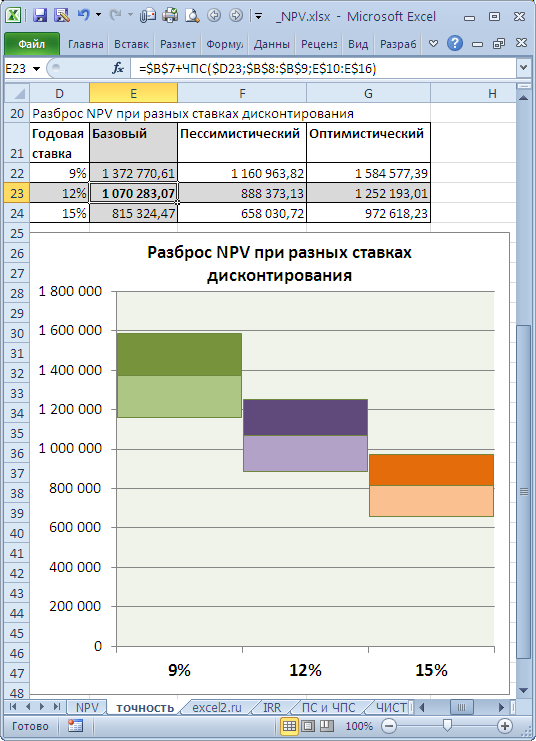
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
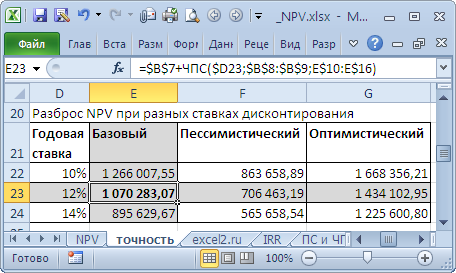
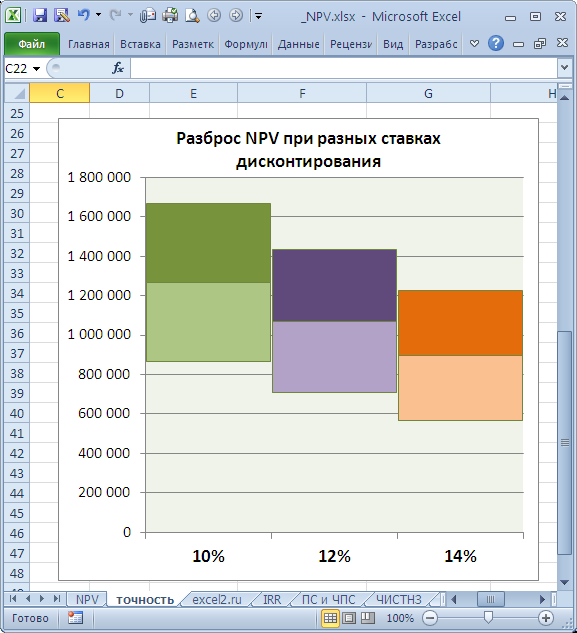
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности IRR (ВСД)
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
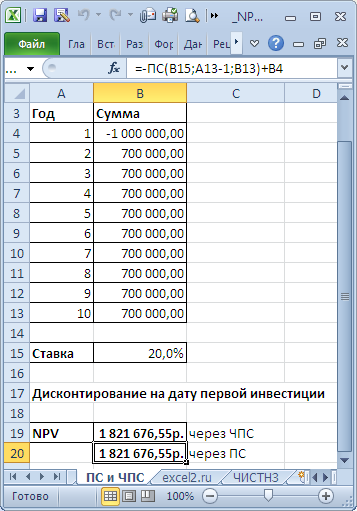
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что аннуитет представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию ПС() (см. файл примера, лист ПС и ЧПС ).
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
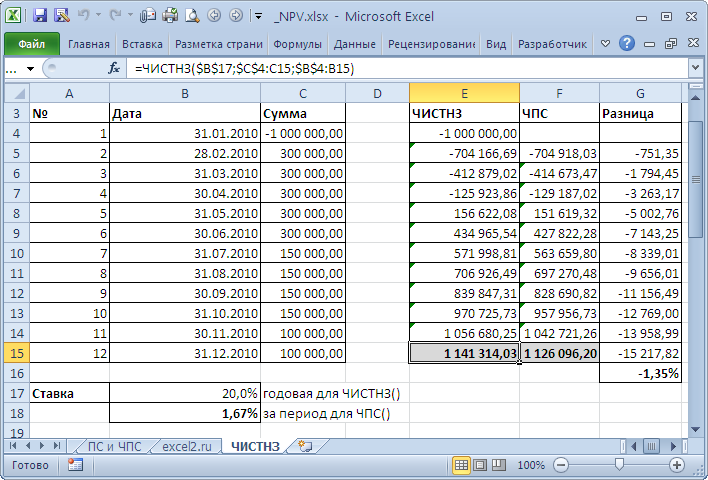
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() (английский вариант – XNPV()).
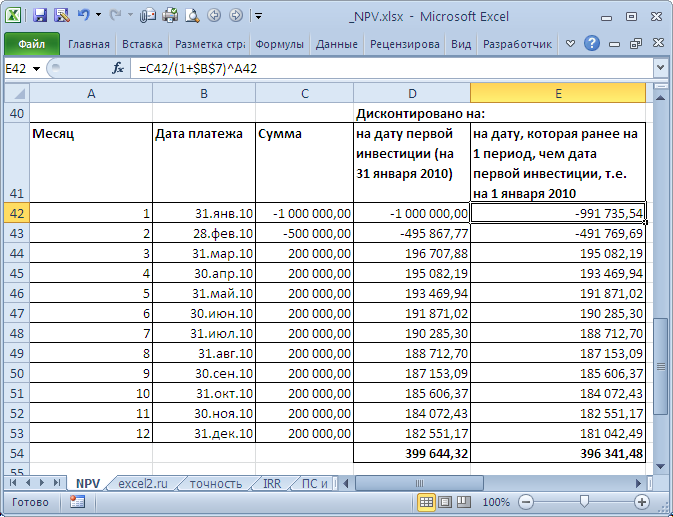
Функция ЧИСТНЗ() возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Это связано с тем, что у ЧИСТНЗ() длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у ЧПС() указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет високосного года).
Внутренняя ставка доходности ЧИСТВНДОХ()
Расчеты в функции ЧИСТВНДОХ() производятся по формуле:
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).