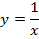Функции f x число t 0 такое что для любого

Периодическая функция

Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).

Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:

Число T называют периодом функции y=f(x).

Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).

Свойства периодических функций

1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).

2) Для любого x из области определения y=f(x) если T₁ — период функции, то

Так как T₂ также является периодом функции y=f(x), то для аргумента x-T₁

Следовательно, число T₁+T₂ является периодом функции y=f(x).

3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.

4) Если T — период функции f(x), то для аргумента kx+b

Значит число T/k — период функции f(kx+b).

5) Эти свойства следуют непосредственно из определения.

Например, для суммы f(x) и g(x):

Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.

Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.

Примеры периодических функций

1) Поскольку для любого x выполняются равенства

то функции y=sin x и y=cos x являются периодическими с периодом T=2π.

2) Так как для любого x из области определения функции y=tg x выполняется равенство

tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.

Аналогично, y=ctg x — периодическая функция с периодом T=π.

3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.

Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.

4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.

Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.

Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.

5) Так как для любого действительного x и любого целого k выполняется равенство =, то функция дробной части числа y= — периодическая с периодом T=k, где k∈Ζ, k≠0.

Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=.

Главный период функций y=sin x и y=cos x T=2π.

Главный период функций y=tg x и y=ctg x T=π.

Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.

То есть любой период функции y=sin x имеет вид 2πn, n∈Z.

Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.

Таким образом, 2π — главный период функции y=sin x.

Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.

Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период

а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период

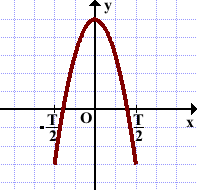
График периодической функции повторяется через промежутки длиной T (на оси Ox).

Дана часть графика

промежутке длиной T.

Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :

Источник

Функции f x число t 0 такое что для любого

376. Транзитивному замыканию бинарного отношения R (a, b): (b — a = 4) удовлетворяет пара
• (12, 28)

377. Транзитивному замыканию бинарного отношения R (a, b): (b/a = 1/3) удовлетворяет пара
• (1, 27)

378. Условной вероятностью события B при условии, что событие A с ненулевой вероятностью произошло, называется:
• р (B/A) = р (AB) / р (A)

379. Формула второго замечательного предела
•

380. Формула первого замечательного предела
•

381. Формула простых процентов, где P — первоначальный вклад, i — процентная ставка, n — число периодов хранения денег, имеет вид
• S = P (1 + n × i)

382. Формула сложных процентов, где P — первоначальный вклад, i — процентная ставка, n — число периодов хранения денег, имеет вид
• S = P (1 + i) n

383. Функция является возрастающей на интервале, если на этом интервале
•

384. Функция является убывающей на интервале, если на этом интервале
•

386. Функция F (x) называется первообразной для функции f (x), если для всех х выполняется равенство
• F¢ (x) = f (x)

387. Функция f (x) называется четной, если для всех x из области определения:
• f (-x) = f (x)

388. Функция называется периодической, если существует такое постоянное число Т 1 0, что для любого x из области определения выполняется равенство
• f (x ± T) = f (x)

389. Функция, задаваемая формулой f (0, Y, Z) X f (1, Y, Z), равна:
• 1

390. Функция, задаваемая формулой &f (0, Y, Z) &X&f (1, Y, Z), равна:
• 0

Источник

Функция

1. Понятие функции

2. Cвойства функций

2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1 ) x2, f(x1) ) f(x2).

область определения (-∞,∞)
область значений (0; ∞)
общего вида
возрастает на (-∞,∞), если a>1;
убывает на (-∞,∞), если 0 непериодическая

Логарифмическая функция

у = log ₐ x (a>0 a≠1)

область определения (0,∞)
область значений (-∞; ∞)
общего вида
возрастает на (0,∞), если a>1;
убывает на (0,∞), 0 непериодическая

Тригонометрические функции

y = sin x

область определения (-∞; ∞)
область значений [-1; 1]
нечетная
возрастает на [-π/2 + 2πn, π/2 + 2πn];
убывает на [π/2 + 2πn, 3π/2 + 2πn], nϵZ;
период Т=2π

y = cos x

область определения (-∞; ∞)
область значений [-1; 1]
четная
возрастает на [-π + 2πn, 2πn];
убывает на [2πn, π + 2πn], nϵZ;
период Т=2π

y = tg x

область определения
(-π/2 + πn, π/2 + πn) nϵZ;
область значений (-∞; ∞)
нечетная
возрастает на (-π/2 + πn, π/2 + πn) nϵZ;
период Т=π

y = ctg x

область определения
(πn, π + πn) nϵZ;
область значений (-∞; ∞)
нечетная
убывает на (πn, π + πn) nϵZ;
период Т=π

y = arcsin x

область определения [-1; 1]
область значений [-π/2; π/2]
нечетная
возрастает на [-1; 1]

y = arccos x

область определения [-1; 1]
область значений [0; π]
функция центрально-симметрична относительно точки (0; π/2)
убывает на [-1; 1]

y = arctg x

область определения (-∞; ∞)
область значений [-π/2; π/2]
нечетная
возрастает на (-∞; ∞)

y = arcctg x

область определения (-∞; ∞)
область значений [0; π]
ни четная, ни нечетная
убывает на (-∞; ∞)

Источник

Функции f x число t 0 такое что для любого

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x₁ Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x₁) ≥ f(x). Аналогично найдётся такая точка x₂, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x₁) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x₂ и x₂‘.

Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a 2

а) в произвольной точке;

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t₀. К этому моменту точка прошла путь s=s(t₀). Определим скорость vматериальной точки в момент времени t₀.

Для этого рассмотрим какой-нибудь другой момент времени t₀+Δt. Ему соответствует пройденный путь s=s(t₀+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t₀+Δt)–s(t).

Рассмотрим отношение . Оно называется средней скоростью в промежутке времени Δt. Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t₀ (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt.

Итак, скоростью движения в данный момент времени t₀ (мгновенной скоростью) называется предел средней скорости в промежутке от t₀ до t₀+Δt, когда Δt→0:

,

т.е. скорость неравномерного движения это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М₀ (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M₀M. Если точка М начинает перемещаться по кривой, а точка М₀ остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М₀ с любой стороны секущая стремится занять положение определенной прямой М₀Т, то прямая М₀Т называется касательной к кривой в данной точке М₀.

Т.о., касательной к кривой в данной точке М₀ называется предельное положение секущей М₀М, когда точка М стремится вдоль кривой к точке М₀.

Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х₀ функция принимает значение y₀=f(x₀). Этим значениям x₀ и y₀ на кривой соответствует точка М₀(x₀; y₀). Дадим аргументу x₀ приращение Δх. Новому значению аргумента соответствует наращенное значение функции y₀+Δ y=f(x₀–Δx). Получаем точку М(x₀+Δx; y₀+Δy). Проведем секущую М₀М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение и заметим, что .

Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М₀. Тогда секущая М₀М будет стремиться занять положение касательной к кривой в точке М₀, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

Т.о., геометрически у ‘(x₀) представляет угловой коэффициент касательной к графику этой функции в точке x₀, т.е. при данном значении аргумента x, производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М₀ (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х 2 в точке М(-1; 1).

Ранее мы уже видели, что (x 2 )’ = 2х. Но угловой коэффициент касательной к кривой есть tg α = y‘|_x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство. Если , то

,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками.

В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – «точка перегиба» cвертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.

Покажем, что она не имеет производной в этой точке.

Т.о., отношение при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная «кривая» не имеет определенной касательной (в этой точке их две).

Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

Источник

Что такое Функция?

7 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

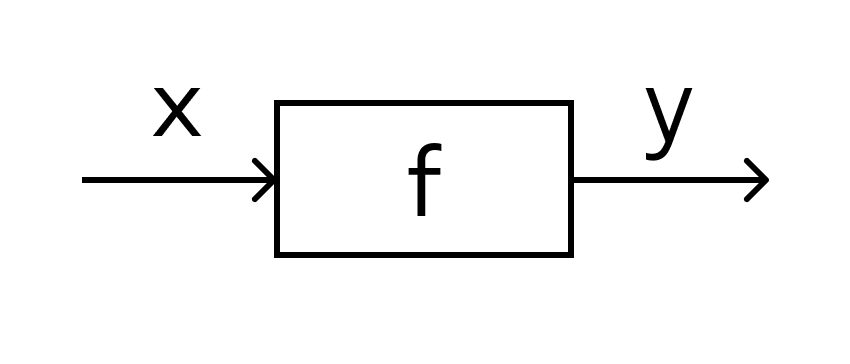
2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник