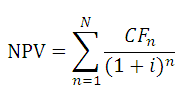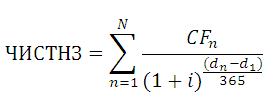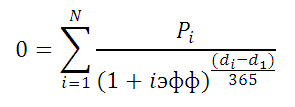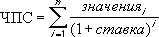Функция чпс в excel что это
Функция чпс в excel что это
Расчет чистой приведенной стоимости в Excel подводит закономерный итог нашим обстоятельным публикациям, посвященным теме приведенной стоимости вообще и чистой приведенной стоимости (NPV) – в частности.
Помимо специальных калькуляторов и таблиц, наиболее эффективным на текущий момент представляется расчет чистой приведенной стоимости именно средствами Excel, хотя бы потому, что это легко, удобно и отвечает современным представлениям об эффективных расчетах.
В сегодняшней статье мы разберем стандартную функцию ЧПС, используемую для нахождения значений чистой приведенной стоимости в таблицах Microsoft Excel, уделив внимание ее синтаксису и приведя несколько наглядных примеров ее практического применения.
Предварительные данные о чистой приведенной стоимости
Освежить свои представления о приведенной и чистой приведенной стоимости можно соответственно здесь и здесь.
Ради экономии вашего (прежде всего) времени ограничусь лишь напоминанием общеизвестной формулы, которую нам придется впоследствии увязывать со стандартной функцией Excel.
Как мы помним, когда речь идет о расчете чистой приведенной стоимости n-ного количества денежных потоков, мы прибегаем к помощи следующей весьма изящной математической конструкции:
Здесь Pi обозначает численное значение денежного потока (которое, кстати говоря, может иметь и отрицательное значение, когда речь идет об оттоках денежных средств), а r – некоторая процентная ставка (ставка дисконтирования).
Разработчики Excel позаботились о том, чтобы предельно упростить стоящую перед нами задачу расчета данного показателя, разработав функцию ЧПС, имеющую следующий формат:
Обязательными в этой функции являются только два параметра: r – размер процентной ставки и P1 – денежный поток в 1-ом периоде. Остальными параметрами можно пренебречь.
Всего формула позволяет обработать 254 значения Pi.
Значения P1, P2, …, Pnмогут быть положительными (в случае ПОСТУПЛЕНИЯ денежных средств) или отрицательными (когда имеют место будущие ВЫПЛАТЫ).
В свою очередь, результат функции ЧПС будет напрямую зависеть от исследуемых эмпирических данных и, как следствие, может принимать как положительные, так и отрицательные значения.
Особенности использования функции ЧПС
Ввести одномоментно 254 значения в одну ячейку бывает весьма утомительно.
Лучше заранее заполнить численными значениями некоторый диапазон, а затем подставлять в формулу ЧПС ссылки на входящие в диапазон ячейки.
Такой подход позволит легко комбинировать данные и исправлять возможные ошибки.
Следует помнить, что для расчета функции ЧПС важен ПОРЯДОК, в котором следуют значения P1, P2, …, Pn. Изменение этого порядка приведет к разным значениям нашей функции.
Предполагается также, что расчет производится для случая, когда выплаты или поступления отстоят друг от друга на один и тот же период (неделя, месяц, год и т.д.), то есть имеет место равномерное распределение денежных потоков во времени.
Все аргументы должны иметь численный формат. Ошибочно введенные в формулу ЧПС буквенные значения или символы при расчетах будут проигнорированы.
Пример расчета чистой приведенной стоимости
Не смею больше испытывать ваше терпение и предлагаю немедля окунуться в завораживающий мир расчета чистой приведенной стоимости с помощью функции ЧПС.
Итак, обещанный пример. Внимательно смотрим на иллюстрацию ниже:
Организуйте на листе вашей таблицы Excel размещение данных, аналогичных вышеприведенным.
Здесь важно заполнить ячейки A1, A2, A3, A4 и A5 конкретными числовыми данными, а в ячейку A7 поместить (важен каждый символ) выражение =ЧПС(A1; A2; A3; A4; A5).
Значение ячейки A7 как раз и будет содержать результат вычисления чистой приведенной стоимости ряда A2:A5.
Соответствующий диапазон, естественно, вы можете расширить или сузить, как вам заблагорассудится, а результирующее значение поместить в любую другую удобную для вас ячейку.
Здесь главное — понять принцип.
Обратите внимание, что значение в ячейке A3 имеет отрицательное значение (-5350).
Это означает, что имеет место выплата денежных средств (что в данном случае соответствует размеру первоначальных инвестиций).
Значения всех следующих аргументов являются положительными, так как мы имеем дело с поступлениями, символизирующими отдачу от наших инвестиций.
Заметим также, что наша функция в ячейке A7 может иметь и более краткий вид: =ЧПС(A1; A2:A5).
Такая запись соответствует синтаксическим стандартам Excel и позволяет сэкономить в ряде случаев и время, и нервы…
Итоговое значение (4110,00р) в денежном формате отображено во все той же ячейке A7.
Обязательно ВРУЧНУЮ проработайте приведенный выше пример.
Вы получите очень важный навык расчета реального финансового показателя – чистой приведенной стоимости — с помощью таблиц Excel.
Если вы планируете серьезно погрузиться в мир инвестиций, вам придется кое-что уметь и кое в чем разбираться.
Умение считать не на бумажке, а с использованием современного программного обеспечения – один из таких навыков.
Дополнительная информация по теме представлена в статье Расчет NPV в Excel (пример).
NPV (чистая приведенная стоимость)
Чистый дисконтированный доход может быть найден за любой период времени проекта начиная с его начала (за 5 лет, за 7 лет, за 10 лет и так далее) в зависимости от потребности расчета.
Для чего нужен
Формула расчета
Для расчета показателя используется следующая формула:
, где
Пример расчета
Для рассмотрения примера расчета показателя NPV возьмем упрощенный проект по строительству небольшого офисного здания. Согласно проекту инвестиций планируются следующие денежные потоки (тыс. руб.):
| Статья | 1 год | 2 год | 3 год | 4 год | 5 год |
| Инвестиции в проект | 100 000 | ||||
| Операционные доходы | 35 000 | 37 000 | 38 000 | 40 000 | |
| Операционные расходы | 4 000 | 4 500 | 5 000 | 5 500 | |
| Чистый денежный поток | — 100 000 | 31 000 | 32 500 | 33 000 | 34 500 |
Подставляя в формулу значения чистого денежного потока за каждый период (там где получается отрицательный денежный поток ставим со знаком минус) и корректируя их с учетом ставки дисконтирования получим следующий результат:
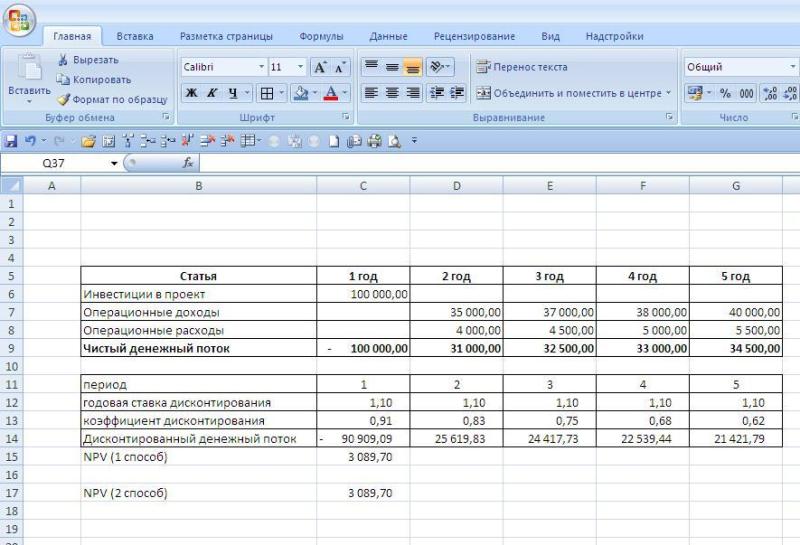
Расчет NPV в Excel
Чтобы проиллюстрировать как рассчитывается NPV в Excel, рассмотрим предыдущий пример заведя его в таблицы. Расчет можно произвести двумя способами
Ниже на рисунке мы привели оба расчета (первый показывает формулы, второй результаты вычислений):
Как вы видите, оба метода вычисления приводят к одному и тому же результату, что говорит о том, что в зависимости от того, чем вам удобнее пользоваться вы можете использовать любой из представленных вариантов расчета.
Примеры расчета NPV в бизнес-планах
Увидеть как рассчитан показатель на конкретном примере бизнес-плана вы можете выбрав соответствующий документ в форме поиска или перейдя по ссылке ниже:
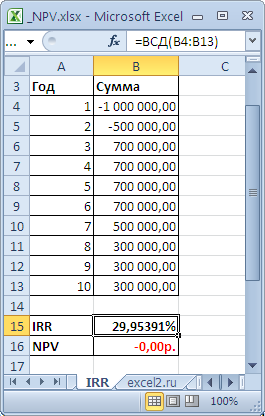
Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в EXCEL
history 3 февраля 2015 г.
Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул MS EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню (взято из Википедии). Или так: Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт cfin. ru) Или так: Текущая стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика . Толковыйсловарь . — М . : « ИНФРА — М «, Издательство « ВесьМир «. Дж . Блэк .)
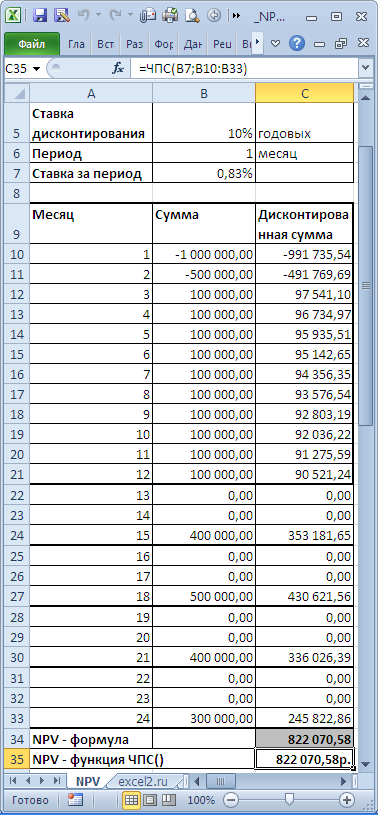
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма Приведенных стоимостей денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Определившись со сроками денежных потоков, для функции ЧПС() нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см. файл примера, лист NPV ).
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).
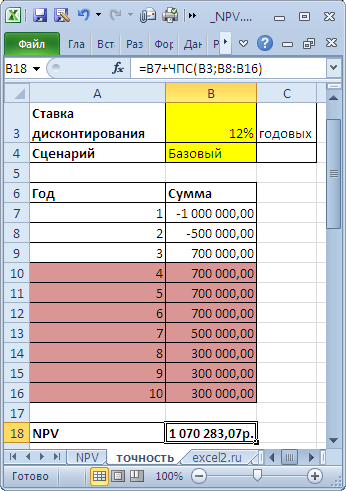
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
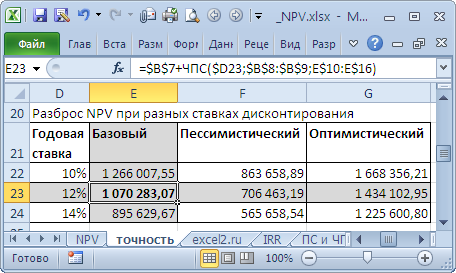
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
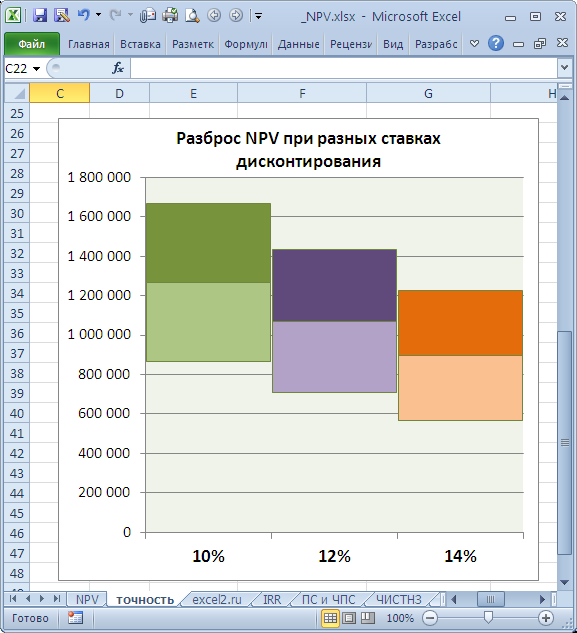
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
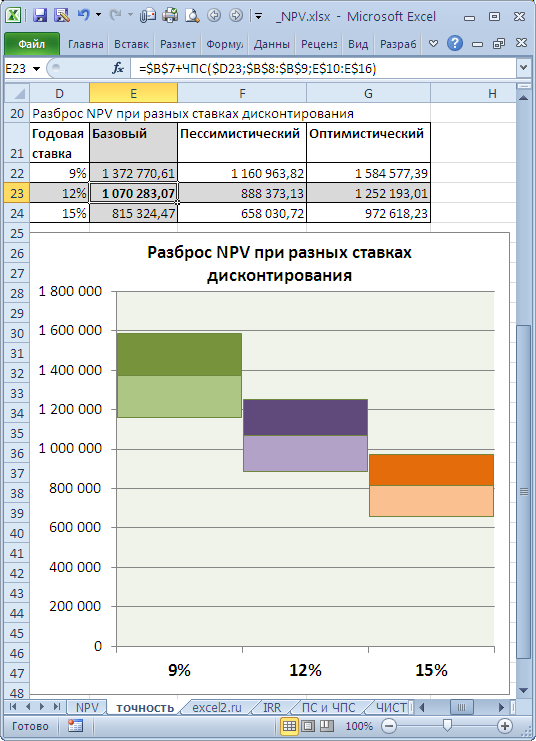
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности IRR (ВСД)
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
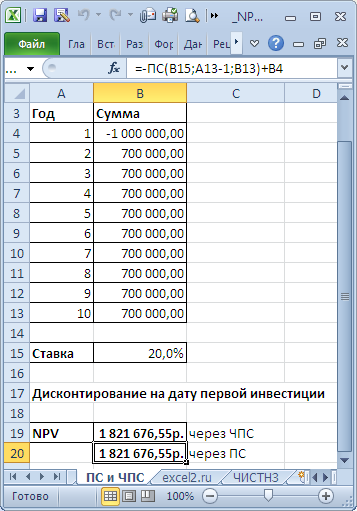
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что аннуитет представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию ПС() (см. файл примера, лист ПС и ЧПС ).
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
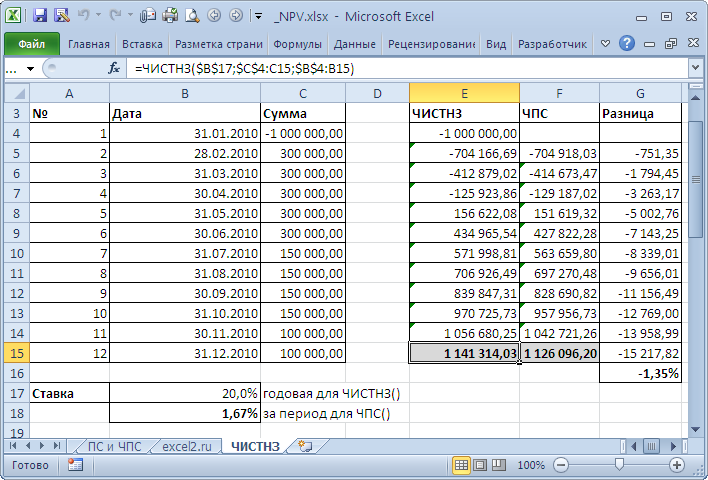
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() (английский вариант – XNPV()).
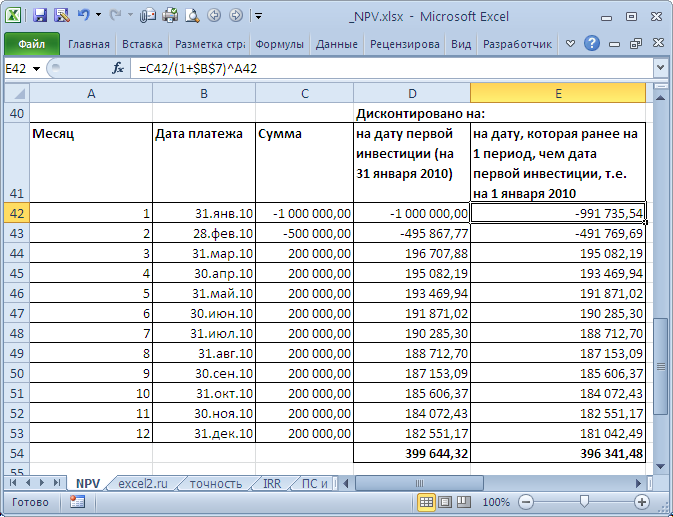
Функция ЧИСТНЗ() возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Это связано с тем, что у ЧИСТНЗ() длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у ЧПС() указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет високосного года).
Внутренняя ставка доходности ЧИСТВНДОХ()
Расчеты в функции ЧИСТВНДОХ() производятся по формуле:
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).
Формула для анализа текущей стоимости инвестиций по ЧПС в Excel
Функция ПС (Приведенная Стоимость) используется для вычисления текущей стоимости денге в Excel, но при условии, что все платежи (выплаты по инвестиционным дивидендам или оплата погашения по кредиту) будут равными суммами. На практике же часто случается, что суммы регулярных выплат бывают разными. Для решения данной задачи программа Excel предлагает функцию ЧПС (Чистая Приведенная Стоимость), которая позволяет вычислить чистую текущую стоимость инвестиций при разных суммах регулярных платежей.
Пример анализа инвестиционного плана с функцией ЧПС в Excel
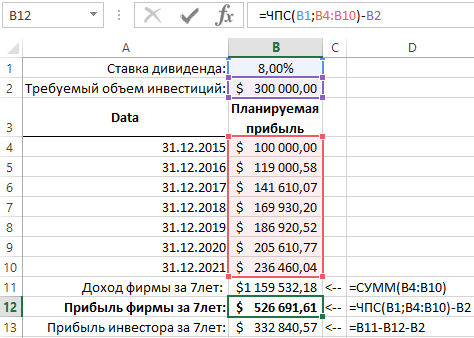
Допустим, молодое предприятие ищет инвестора, который проинвестирует его на сумму 300 000$. По договору предприятие обязуется на протяжении семи лет ежегодно выплачивать инвестору дивиденды. Оценка планируемой прибыльности предприятия за каждый год при данном объеме инвестиций на старте изображена в графике ниже на рисунке. Планируемая доходность данного инвестиционного проекта для инвестора составляет 8% годовых.
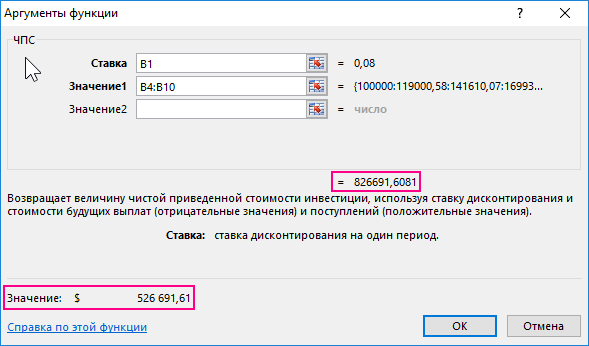
Чтобы проанализировать рациональность привлечения инвестиций под 8% годовых в данное предприятие используется функция ЧПС, которая вычисляет чистую текущую стоимость вложенных финансовых средств.
Функция ЧПС дисконтирует с определенной процентной ставкой каждую дивидендную выплату по отдельности подобно, как и функция ПС, но немного по-другому. В Функции ЧПС используется диапазон значений всех платежей будущих доходов, а не одна сумма платежа. Существенным отличием также является тот факт, что функция ЧПС не имеет аргумента «Количество периодов (Кпер)», так как количество указанных значений в диапазоне и определяет количество будущих платежей:
Хоть платежи могут иметь разные суммы, все же они должны выплачивается регулярно (в данном примере – ежегодно). Кроме того, также, как и в других финансовых функциях Excel вычисляющих стоимость денег во времени, процентная ставка должна соответствовать согласно периодами платежей (процентов годовых, ежемесячных или ежедневных). В данном примере принята процентная ставка 8% годовых, а регулярность платежей так же ежегодно – значит входящие данные согласованы между собой. Если бы дивиденды выплачивались ежеквартально, тогда необходимо было-бы использовать ежеквартальную процентную ставку (8%/4 – восемь процентов годовых разделить на 4 квартала, в результате получим 2% ежеквартальных).
В предыдущем примере инвестору необходимо было в самом начале сделать большую инвестицию, чтобы в будущем получить прибыль. Функцию ЧПС можно также использовать и в других ситуациях. Например, инвестор должен делать инвестиционные взносы, разбитые на меньшие суммы вначале инвестирования, а под конец получать доходы от вложенных средств.
Анализ текущей стоимости денег при разных суммах взносов и выплат
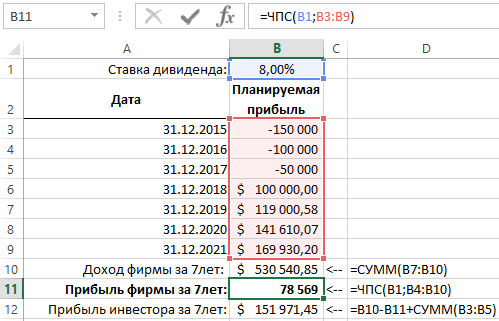
Допустим, что вместо разового инвестиционного взноса 300 000$ можно вложить только 150 000$ в первом году, 100 000$ – во втором и 50 000$ – в третьем году. Суммы, которые будут инвестированы уменьшаются в меру развития предприятия так как с каждым годом оно может позволить себе использовать большую сумму рефинансирования своих собственных средств. На четвертый год не обязательно уже инвестировать, так как ожидается что предприятие буде уже на столько прибыльным, что будет иметь возможность начинать выплачивать дивиденды.
Ниже на рисунке изображен график инвестиционных взносов на протяжении 3-х лет и выплаты дивидендов на протяжении остальных 4-х лет. Используется та же функция ЧПС, что и в предыдущем примере изменены только входящие значения и нет вычитания в формуле, так как в аргументах функции уже используются отрицательные числа:
В первом примере инвестированная сумма не использовалась в вычислениях функции ЧПС. Просто итоговый результат вычисления сравнивался с объемом необходимых инвестиционных средств. В данном примере инвестированная сумма, разбитая на части и все они выражены отрицательными числами (расход), а суммы прибыли фирмы выражены положительными числами (приход).
Работа с денежными потоками: вычисление показателей ЧПС и ВСД в Excel
Вы теряете спящий режим и знаете, как максимально повысить прибыльность и свести к минимуму риски, связанные с бизнес-инвестициями? Остановить переключение и поворот. Расслабьтесь и перейти к потоку.
Наличные, то есть. Взгляните на движение денежных средств, а также на то, что выходит за рамки вашей компании. Положительный денежный поток — это показатель получения денежных средств (продажи, проценты, проблемы с акциями и так далее), тогда как отрицательный денежный поток — это показатель выходных денежных средств (покупки, выплаты, налоги и так далее). Чистое движение денежных средств — это разница между положительным и отрицательным денежными потоками и ответы на наиболее фундаментальные деловые вопросы о том, сколько денег осталось в хлеве?
Для развития бизнеса необходимо принимать ключевые решения о том, куда вкладывать деньги в долгосрочной перспективе. Microsoft Excel сравните параметры и сделайте правильный выбор, чтобы можно было отдохнуть как днем, так и ночью.
Вопросы о проектов по capital investment
Если вы хотите взять деньги с себя, сделать его рабочим и вкладывать их в проекты, которые составляют вашу бизнес, вам нужно задать несколько вопросов об этих проектах:
Будет ли новый долгосрочный проект прибыльным? Когда?
Лучше ли вкладывать деньги в другой проект?
Следует ли вкладывать средства в текущий проект еще больше или стоит ли сократить потери?
Теперь рассмотрим каждый из этих проектов подробнее и спросите:
Каковы отрицательные и положительные денежные потоки для этого проекта?
Какое влияние оказывают крупные первоначальные инвестиции и какой объем будет слишком велик?
В итоге вам действительно нужны номера нижней строки, которые можно использовать для сравнения вариантов проектов. Но для этого необходимо включить в анализ значения времени денежных средств.
Ответы на вопросы с помощью ЧПС и IRR
Существует два финансовых способа, которые помогут вам ответить на все эти вопросы: чистая стоимость (ЧПС) и внутренняя ставка прибыли (IRR). Как ЧПС, так и IRR называются дисконтируемыми методами движения денежных средств, так как они применяют значение времени к оценке проектов по capital investment. Как ЧПС, так и IRR основаны на рядах будущих платежей (отрицательный денежный поток), доходов (положительный денежный поток), потерь (отрицательный денежный поток) или «нулевых денежных потоков».
ЧПС возвращает чистую стоимость денежных потоков, представленных в современных рублях. Из-за денежной стоимости каждый доллар сегодня стоит больше, чем завтра. ЧПС вычисляет обтекаемую стоимость для каждого ряда денежных потоков и объединяет их, чтобы получить чистую стоимость.
Где n — количество денежных потоков, а i — процентная или скидка.
IRR основан на ЧПС. Это можно представить в особом случае ЧПС, где вычисляемая ставка прибыли представляет процентную ставку, соответствующую нулевой (нулевой) чистой стоимости.
Если все отрицательные денежные потоки происходят раньше всех положительных или когда последовательность денежных потоков проекта содержит только один отрицательный денежный поток, IRR возвращает уникальное значение. Большинство проектов по инвестиции в основном начинаются с больших отрицательных денежных потоков (в начале инвестиции), за которыми следуют положительные денежные потоки, и, следовательно, имеют уникальный IRR. Однако иногда может быть несколько допустимых IRR или вообще ничего.
Сравнение проектов
ЧПС определяет, должен ли проект получить больше или меньше желаемой ставки прибыли (уровень сложности), и хорошо определяет, будет ли проект прибыльным. IRR на один шаг дальше, чем ЧПС, чтобы определить определенную ставку прибыли для проекта. Как ЧПС, так и IRR — это числа, которые можно использовать для сравнения проектов и выбора оптимальных вариантов для вашей компании.
Выбор соответствующей Excel функции
hich Office Excel функции, которые можно использовать для вычисления ЧПС и IRR? Существует пять: функция ЧПС,функция ЧПС,функция IRR,ФУНКЦИЯ XIRRи МВСД. Выбор зависит от предпочитаемого финансового метода, от того, происходят ли денежные потоки через определенные интервалы времени и являются ли они периодическими.
Примечание: Денежные потоки заданы как отрицательные, положительные или нулевые значения. При использовании этих функций обратите особое внимание на то, как вы обрабатываете мгновенные денежные потоки, которые происходят в начале первого периода, и все остальные денежные потоки, которые происходят в конце периодов.
Используйте, когда нужно
Определите чистую стоимость на основе денежных потоков, которые происходят регулярно, например ежемесячно или ежегодно.
Каждый денежный поток, заданный как значение,происходит в конце периода.
Если в начале первого периода имеется дополнительный денежный поток, он должен быть добавлен к значению, возвращаемом функцией ЧПС. См. пример 2 в разделе справки по функции ЧПС.
Определите чистую стоимость на основе денежных потоков, которые возникают через нерегулярные интервалы.
Каждый денежный поток, указанный как значение, происходит в запланированную дату платежа.
Определите внутреннюю ставку прибыли с использованием денежных потоков, которые происходят регулярно, например ежемесячно или ежегодно.
Каждый денежный поток, заданный как значение,происходит в конце периода.
Если имеется несколько допустимых ответов, функция IRR возвращает только первый из них. Если IRR не находит ответ, возвращается #NUM! значение ошибки #ЗНАЧ!. Используйте другое значение для предположения, если вы получаете ошибку или результат отличается от ожидаемого.
Примечание. Другой вариант может возвращать другой результат, если имеется более одной внутренней ставки прибыли.
ФУНКЦИЯ XIRR (значения, даты, [предположение])
Определите внутреннюю ставку прибыли с помощью денежных потоков, которые возникают через нерегулярные интервалы.
Каждый денежный поток, указанный как значение, происходит в запланированную дату платежа.
Если имеется несколько допустимых ответов, функция XIRR возвращает только первый из них. Если xiRR не находит ответ, возвращается #NUM! значение ошибки #ЗНАЧ!. Используйте другое значение для предположения, если вы получаете ошибку или результат отличается от ожидаемого.
Примечание. Другой вариант может возвращать другой результат, если имеется более одной внутренней ставки прибыли.
Функция MIRR (значения, finance_rate, reinvest_rate)
Определите модифицированную внутреннюю ставку прибыли с использованием денежных потоков, которые происходят регулярно, например ежемесячно или ежегодно, и учитывайте как стоимость инвестиций, так и проценты, полученные от реинвестирования денежных средств.
Каждый денежный поток, заданный как значение,происходит в конце периода, за исключением первого денежного потока, который определяет значение в начале периода.
Процентная ставка, которую вы платите с денежных средств, используемых в денежных потоках, указана в finance_rate. Процентная ставка, получаемая для денежных потоков при реинвестирования, указывается в reinvest_rate.