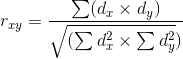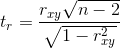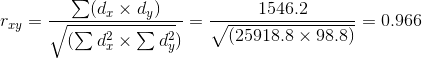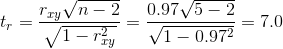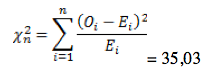Хи квадрат пирсона что показывает
Проверка гипотез критерием хи-квадрат Пирсона
Автор материала: Пятницкий А.М. (bioinformatics.ru/Data-Analysis/Pearson_chisquare_distance.html)
Хи-квадрат критерий – универсальный метод проверки согласия результатов эксперимента и используемой статистической модели.
Расстояние Пирсона X 2
Российский Государственный Медицинский Университет
В 1900 году Карл Пирсон предложил простой, универсальный и эффективный способ проверки согласия между предсказаниями модели и опытными данными. Предложенный им “хи-квадрат критерий” – это самый важный и наиболее часто используемый статистический критерий. Большинство задач, связанных с оценкой неизвестных параметров модели и проверки согласия модели и опытных данных, можно решить с его помощью.
Применение хи-квадрат критерия для проверки простых гипотез.
Квадрат обычного евклидова расстояния был бы равен:
X 2 Euclid = S (Oi-Ei) 2 = (5-10) 2 +(15-10) 2 + (6-10) 2 +(14-10) 2 +(4-10) 2 +(16-10) 2
X 2 Pearson = (5-10) 2 /10+(15-10) 2 /10 +(6-10) 2 /10+(14-10) 2 /10+(4-10) 2 /10+(16-10) 2 /10=15.4
Для правильной игральной кости все ожидаемые частоты Ei одинаковы, но обычно они различны, поэтому поверхности, на которых расстояние Пирсона постоянно ( X 2 Pearson =const) оказываются уже эллипсоидами, а не сферами.
Пирсон определил случайную величину χ 2 n – “хи-квадрат с n степенями свободы”, как сумму квадратов n независимых стандартных нормальных с.в.:
Попытаемся наглядно понять смысл этой важнейшей в статистике случайной величины. Для этого на плоскости (при n =2) или в пространстве (при n =3) представим облако точек, координаты которых независимы и имеют стандартное нормальное распределение f T ( x )
f χ 2 2 (a) = С exp(-a/2) = 0.5exp(-a/2).
При достаточно большом числе степеней свободы n ( n >30) хи-квадрат распределение приближается к нормальному: N ( m = n ; σ = (2 n ) ½ ). Это следствие “центральной предельной теоремы”: сумма одинаково распределенных величин имеющих конечную дисперсию приближается к нормальному закону с ростом числа слагаемых.
После выяснения ошибки, существовавшие таблицы χ 2 пришлось дополнить, так как исходно в них не было случая n =1, так как наименьшее число разрядов =2. Теперь же оказалось, что могут быть случаи, когда расстояние Пирсона имеет распределение χ 2 n =1.
Пример. При 100 бросаниях монеты число гербов равно O 1= 65, а решек O 2= 35. Число разрядов M =2. Если монета симметрична, то ожидаемые частоты E 1=50, E 2=50.
X 2 Pearson = S (Oi-Ei) 2 /Ei = (65-50) 2 /50 + (35-50) 2 /50 = 2*225/50 = 9.
=(Nν-Np) 2 (1/p + 1/(1-p))/N=(Nν-Np) 2 /(Np(1-p))=( (K-Np)/(Npq) ½ ) 2 = T 2
До сих пор мы рассматривали простые гипотезы, для которых ожидаемые средние частоты Ei полностью известны заранее. О том, как правильно выбирать число степеней свободы для сложных гипотез см. ниже.
Применение хи-квадрат критерия для проверки сложных гипотез
В примерах с правильной игральной костью и монетой ожидаемые частоты можно было определить до(!) проведения опыта. Подобные гипотезы называются “простыми”. На практике чаще встречаются “сложные гипотезы”. При этом для того, чтобы найти ожидаемые частоты Ei надо предварительно оценить одну или несколько величин (параметры модели), и сделать это можно только, воспользовавшись данными опыта. В результате для “сложных гипотез” ожидаемые частоты Ei оказываются зависящими от наблюдаемых частот Oi и потому сами становятся случайными величинами, меняющимися в зависимости от результатов опыта. В процессе подбора параметров расстояние Пирсона уменьшается – параметры подбираются так, чтобы улучшить согласие модели и опыта. Поэтому число степеней свободы должно уменьшаться.
Как оценить параметры модели? Есть много разных способов оценки – “метод максимального правдоподобия”, “метод моментов”, “метод подстановки”. Однако можно не привлекать никаких дополнительных средств и найти оценки параметров минимизируя расстояние Пирсона. В докомпьютерную эпоху такой подход использовался редко: при ручных расчетах он неудобен и, как правило, не поддается аналитическому решению. При расчетах на компьютере численная минимизация обычно легко осуществляется, а преимуществом такого способа является его универсальность. Итак, согласно “методу минимизации хи-квадрат”, мы подбираем значения неизвестных параметров так, чтобы расстояние Пирсона стало наименьшим. (Кстати, изучая изменения этого расстояния при небольших смещениях относительно найденного минимума можно оценить меру точности оценки: построить доверительные интервалы.) После того как параметры и само это минимальное расстояние найдено опять требуется ответить на вопрос достаточно ли оно мало.
Общая последовательность действий такова :
где α – “уровень значимости” или ”размер критерия” или “величина ошибки первого рода” (типичное значение α=0.05).
Обычно число степеней свободы n вычисляют по формуле
n = (число разрядов) – 1 – (число оцениваемых параметров)
Если X 2 > χ 2 крит, то гипотеза H 0 отвергается, в противном случае принимается. В α∙100% случаев (то есть достаточно редко) такой способ проверки H 0 приведет к “ошибке первого рода”: гипотеза H 0 будет отвергнута ошибочно.
Пример. При исследовании 10 серий из 100 семян подсчитывалось число зараженных мухой-зеленоглазкой. Получены данные: Oi =(16, 18, 11, 18, 21, 10, 20, 18, 17, 21);
Можно ли считать эти данные однородными?
Здесь неизвестен заранее вектор ожидаемых частот. Если данные однородны и получены для биномиального распределения, то неизвестен один параметр доля p зараженных семян. Заметим, что в исходной таблице фактически имеется не 10 а 20 частот, удовлетворяющих 10 связям: 16+84=100, … 21+79=100.
X 2 = (16-100p) 2 /100p +(84-100(1-p)) 2 /(100(1-p))+…+
(21-100p) 2 /100p +(79-100(1-p)) 2 /(100(1-p))
Объединяя слагаемые в пары (как в примере с монетой), получаем ту форму записи критерия Пирсона, которую обычно пишут сразу:
X 2 = (16-100p) 2 /(100p(1-p))+…+ (21-100p) 2 /(100p(1-p)).
Важные моменты
Оценка параметров. Использование “самодельных”, неэффективных методов оценки может привести к завышенным значениям расстояния Пирсона.
Выбор правильного числа степеней свободы. Если оценки параметров делаются не по частотам, а непосредственно по данным (например, в качестве оценки среднего берется среднее арифметическое), то точное число степеней свободы n неизвестно. Известно лишь, что оно удовлетворяет неравенству:
Результаты А: 25, 24, 26, 25, 24. Вывод исследователя: закон Менделя справедлив(?).
Результаты B : 29, 21, 23, 30, 19. Вывод исследователя: закон Менделя не справедлив(?).
Однако закон Менделя имеет статистическую природу, и количественный анализ результатов меняет выводы на обратные! Объединив пять опытов в один, мы приходим к хи-квадрат распределению с 5 степенями свободы (проверяется простая гипотеза):
X 2 A = ((25-25) 2 +(24-25) 2 +(26-25) 2 +(25-25) 2 +(24-25) 2 )/(100∙0.25∙0.75)=0.16
X 2 B = ((29-25) 2 +(21-25) 2 +(23-25) 2 +(30-25) 2 +(19-25) 2 )/(100∙0.25∙0.75)=5.17
Среднее значение m [ χ 2 n =5]=5, среднеквадратичное отклонение σ[ χ 2 n =5]=(2∙5) 1/2 =3.2.
Поэтому без обращения к таблицам ясно, что значение X 2 B типично, а значение X 2 A неправдоподобно мало. Согласно таблицам P ( χ 2 n =5 A был сторонником генетики, а исследователь B – ее противником.
Критерий Пирсона не всесилен. Существует бесконечное множество альтернатив для H 0, которые он не в состоянии учесть. Пусть вы проверяете гипотезу о том, что признак имел равномерное распределение, у вас имеется 10 разрядов и вектор наблюдаемых частот равен (130,125,121,118,116,115,114,113,111,110). Критерий Пирсона не c может “заметить” того, что частоты монотонно уменьшаются и H 0 не будет отклонена. Если бы его дополнить критерием серий то да!
Критерий хи-квадрат (Chi-Square Statistic)
Данные, используемые при вычислении этой Статистики (Statistics), должны быть случайными, необработанными, взаимоисключающими, взятыми из независимых переменных и взятыми из достаточно большой Выборки (Sample). Например, результаты подбрасывания монеты соответствуют этим критериям.
При проверке гипотез часто используется критерий Хи-квадрат. Статистика сравнивает размер любых расхождений между ожидаемыми и фактическими результатами, учитывая размер выборки и количество переменных. Для этих тестов используются Степени свободы (Degrees of Freedom), чтобы определить, можно ли отклонить определенную Нулевую гипотезу (Null Hypothesis) на основе общего количества переменных и выборок в эксперименте. Как и в случае с любой другой статистикой, чем больше размер выборки, тем надежнее результаты.
Существует два основных вида тестов хи-квадрат: тест на независимость, который задает вопрос о взаимоотношениях, например: «Есть ли связь между полом студента и выбором курса?»; и тест согласия, который спрашивает что-то вроде «Насколько хорошо монета в моей руке соответствует теоретически «честной» монете?»
Независимость
При изучении взаимосвязи между полом учащегося и выбранным курсом можно использовать критерий χ2 на независимость. Для проведения этого теста исследователь собирал данные по двум выбранным переменным (пол и выбранные курсы), а затем сравнивал частоту, с которой учащиеся мужского и женского пола выбирали среди предлагаемых классов, используя формулу, приведенную выше, и специальную статистическую таблицу.
Если нет взаимосвязи между полом и выбором курса (то есть, если они независимы), то следует ожидать, что фактическая частота, с которой студенты мужского и женского пола выбирают каждый предлагаемый курс, будет примерно равной. Число учащихся женского пола на любом выбранном курсе должно быть примерно равным доле студентов мужского в выборке. Тест на независимость может охарактеризовать разницу между фактическим наблюдением и теоретическим ожиданием.
Адекватность модели
Критерий Хи-квадрат предоставляет способ проверить, насколько хорошо выборка соответствует характеристикам Генеральной совокупности (Population). Мы не будем использовать выборку, если она не соответствует ожидаемым свойствам интересующей нас совокупности.
Пример. Рассмотрим воображаемую монету с вероятностью выпадения орла или решки ровно 50/50 и реальную монету, которую вы подбрасываете 100 раз. Если эта реальная монета имеет «справедливую» форму, то она также будет иметь равную вероятность приземления с обеих сторон, и ожидаемый результат подбрасывания монеты: орел выпадет 50 раз, и решка столько же. В этом случае критерий может сказать нам, насколько хорошо фактические результаты 100 подбрасываний монеты сравниваются с теоретической моделью, согласно которой честная монета даст результат 50/50. Фактический бросок может составить 50/50, 60/40 или даже 90/10. Чем дальше фактические результаты от 50/50, тем меньше соответствие этого набора бросков теоретическому ожиданию 50/50 и тем более вероятно, что эта монета на самом деле несправедлива.
Критерий Хи-квадрат и SciPy
Критерий можно вычислить с помощью функции SciPy. Для начала импортируем необходимые библиотеки:
Переформатируем целевую переменную с помощью метода vstack() ^ то есть превратим массивы 1-y и y в вертикальные массивы. Выполним Векторное перемножение (Dot Product) X и Y и посмотрим на результат:
Это наблюдаемые частоты признаков для каждого класса, то есть Таблица сопряжённости (Contingency Table):
Теперь вычислим ожидаемые значения:
Ожидаемые частоты выглядят так:
Наконец проведем тест Хи-квадрат, и для этого создадим два объекта score – результаты теста, и pval – P-значение (P-Value):
Реальные записи довольно плохо соответствуют ожидаемым, и это легко заметить по среднему низкому значению теста. Интересно, что создатели предполагают отображение 8 знаков после запятой, потому третий элемент ряда, «закончившийся» после третьего знака, так забавно выглядит:
Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА
– это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, изменяется ли (возрастает или уменьшается) один показатель в ответ на изменения другого? В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy.
1. История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
2. Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
4. Как рассчитать коэффициента корреляции Пирсона?
Расчет коэффициента корреляции Пирсона производится по следующей формуле:
5. Как интерпретировать значение коэффициента корреляции Пирсона?
Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.
6. Пример расчета коэффициента корреляции Пирсона
Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:
Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769
Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441
Mx = Σ(X) / n = 4769 / 5 = 953.8
My = Σ(Y) / n = 441 / 5 = 82.2
Основные статистические критерии. Критерий Хи-квадрат Пирсона
Психология – уникальная наука, которая сочетает в себе самые разные приемы и элементы. Она исследует взаимоотношения людей, душевное и психологическое равновесие, помогает решать многочисленные задачи путем нефизического (морального, духовного и иного) воздействия.
Психология – уникальная наука, которая сочетает в себе самые разные приемы и элементы. Она исследует взаимоотношения людей, душевное и психологическое равновесие, помогает решать многочисленные задачи путем нефизического (морального, духовного и иного) воздействия.

Для того чтобы правильно подобрать инструмент, необходимо досконально ознакомиться с ситуацией, выявить все возможные факторы, причины и следствия, собрать максимум информации и статистических данных по изучаемой проблеме. Здесь важно не просто наблюдать за происходящим, но и грамотно оценить обстоятельства и результаты, уметь пользоваться теоретическими и статистическими данными.
Для сравнения различных материалов используются специфические приемы, которые основываются на статистике, математике, моделировании и пр. Одним из таких методов является Хи-квадрат Пирсона.
Что это такое?
Хи-квадрат Пирсона – уникальная методика, позволяющая сравнить качественные характеристики, проанализировать частоты и выявить закономерности и тенденции развития испытуемой группы.
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Данное правило успешно применяется для оценки воздействующих на исход исследования факторов. Здесь наблюдается сочетание частот (количественное измерение объекта исследования) с качественными характеристиками. Фактически он позволяет сопоставить опытные данные с теоретическими представлениями, проанализировать сходства и различия, наличие отклонений и пр.
Хи-квадрат Пирсона применяется в ходе анализа так называемых таблиц сопряжения, которые содержат сведения о частоте исходов в зависимости от воздействующих параметров.
Таблицы сопряженности могут быть как простыми, так и сложными. Приведем пример простейшего варианта.

Таблицы сопряженности позволяют представить полученные сведения в более простом для анализа виде. Они напрямую связывают факторы и результаты, уточняя связь статистически данных, минимизируя случайные связи и погрешности.
Правила применения Хи-квадрата Пирсона
Каждая методика применима в определенных случаях и имеет ряд ограничений. В данном случае необходимо соблюдать следующие требования:
Алгоритм расчетов по методу Хи-квадрат Пирсона
В основе действия данного принципа лежит сравнение между существующими частотами (реальность) и рассчитанными показателями (гипотетическими частотами). Если различия между реальными и «гипотетическими» данными малые, то исследователь принимает за истину основную гипотезу. Если же реальные и теоретические данные кардинально разнятся, то нулевая (основная) гипотеза отвергается из-за установления статистически значимых различий.
Чем выше значения Хи-квадрата, тем больше вероятность того, что исследователю придется отвергнуть нулевую идею. Притом важно учесть, что изначально основная гипотеза считается истинной до тех пор пока она не получит достойное опровержение.
В основе методики Хи-квадрат Пирсона лежат следующие показатели:
После сравнения полученного результата Хи-квадрата и критической области исследователю необходимо грамотно интерпретировать вывод. Если Хи-квадрат превосходит критическое значение, то это свидетельствует о наличии статистической связи между явлением и результатом с учетом уровня значимости.
Методика Хи-квадрат Пирсона применима для проверки простых и сложных гипотез. Главное, учитывать все факторы и действовать согласно установленным правилам.
Рассмотрим действие правила Пирсона на конкретном примере.

Команда ОЦ Дисхелп готова помочь в выполнении психологических исследований, студенческих и научных работ по этому направлению. Наши специалисты подберут подходящую методику, произведут все необходимые расчеты и сравнения, грамотно сформулируют выводы. У нас трудятся теоретики и практики, готовые поделиться информацией и опытом. Мы гарантируем высокое качество услуг, индивидуальный подход и конфиденциальность данных!
Трудности с учебой?
Помощь в написании студенческих и
аспирантских работ!
Хи-квадрат (χ 2 ) Пирсона: условия применения метода и интерпретация
Хи-квадрат Пирсона один из самых популярных статистических критериев для анализа качественных данных (номинальных, порядковых, ранговых), анализа частот. Однако, как и у каждого статистического критерия у хи-квадрата есть свои собственные правила применения метода, его интерпретации. Для того, чтобы Вы могли успешно овладеть этим ценнейшим статистическим инструментом сравнения статистических совокупностей по качественным данным предлагаем Вам ознакомиться с этой учебной статьей.
Как использовать хи-квадрат Пирсона?
Хи-квадрат используется прежде всего для анализа таблиц сопряженности (вид таблицы, которая учитывает совместное влияние фактора на исход, данные в таблице сопряженности должны быть представлены в виде частоты номинальных данных или интервалами, но не непрерывными количественными величинами). Стоит отметить, что при работе с сопряженными таблицами хи-квадрат часто является поддержкой для анализа влияния факторов риска с помощью расчета рисков (абсолютный и относительный риски) и отношение шансов.
Таблицы сопряженности могут принимать различные формы, простейшая таблица сопряженности выглядит следующим образом:
| Исход есть | Исхода нет | Всего | |
| Фактор риска есть | A | B | A+B |
| Фактора риска нет | C | D | C+D |
| Всего | A+C | B+D | A+B+C+D |
Как заполнить таблицу сопряженности? Обратимся к простому примеру:
Например, Вы хотите с помощью таблицы сопряженности и как следствия хи-квадрата Пирсона выяснить есть ли различия в частоте артериальной гипертонии в группах курящего и некурящего населения. Предполагается, что по остальным параметрам Ваши группы равномерны и превалирующим фактором риска развития артериальной гипертензии будет именно курение.
Для проведения исследования на основании ретроспективных данных (дизайн: случай-контроль) были отобраны две группы исследуемых — в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую группу вошли 80 некурящих такого же возраста, пола, и социального уровня (прочие систематически ошибки случайны).
В первой группе у 40 человек отмечалась артериальная гипертензия. Во второй — у 32 человек. Соответственно, референсное (нормальное) артериальное давление в группе «курильщиков» наблюдалось у 30 человек (70 — 40 = 30), а в группе «некурящих» нормальное АД наблюдалось у 48 (80 — 32 = 48).
Имея эти данные мы можем заполнить простейшую таблицу сопряженности:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
АД- артериальное давление
Как видно из таблицы: каждая строка соответствует группе пациентов, которая подвергается влиянию фактора, каждый столбец, в свою очередь, обозначает частоту исходов в группе (к примеру: произошло/ не произошло, как в нашем примере).
Таблицы сопряженности служат удобным средством визуализации комбинации частот «фактор- исход» и субстратом для расчета хи-квадрата Пирсона, который в нашем случае сможет дать статистически точный ответ о случайности или не случайности наших находок.
Условия применения статистического критерия хи-квадрата Пирсона
бинарными (пол: мужской/женский, наличие или отсутствие заболевания)
порядковыми (степень артериальной гипертензии),
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 49/13=3,77 | 16/12=1,33 | 9/5=1,80 |
| III | 81/34=2,38 | 144/32=4,50 | 9/14=0,64 |
| IV | 256/26=9,85 | 256/24=10,66 | 0/10*=0,10 |
| Всего | 16 | 16,49 | 2,54 |
как видно из данной таблицы одно из ожидаемых значений равно 0, в данном случае будет подставлена 1, корректнее применить точный критерий Фишера (см. Условия применения хи-квадрата Пирсона)
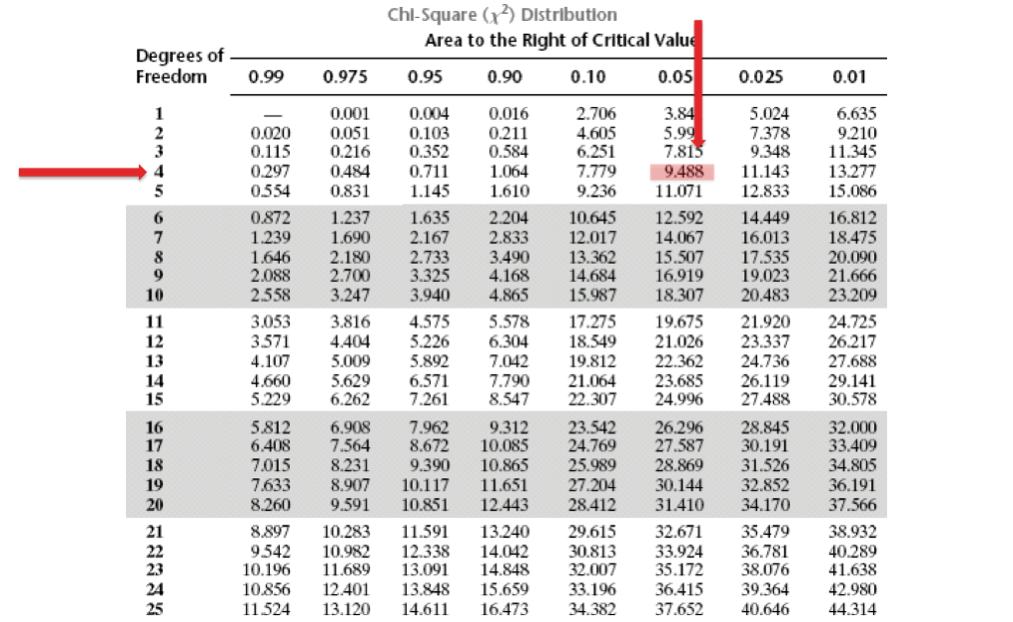
Четвертый этап
Необходимо соотнести полученное значение хи-квадрата с критическим значением хи-квадрата.Возникает вопрос, откуда брать критическое значение? Критическое значение хи-квадрата, как и для большинства, статистических критериев зависит от степени свободы и уровня достоверности (alpha), который Вы выбираете.В нашем случае, наше количество степеней свободы равно (3-1)*(3-1)=4, уровень значимости, который мы хотим соблюсти равен 0,05Обратимся к таблице критических значение хи-квадрата: