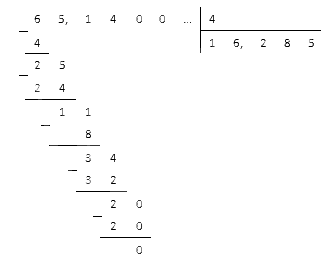Как сделать деление десятичных дробей
Деление десятичных дробей: правила, примеры, решения
Содержание:
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
Точность результата будет зависеть от степени округления.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Решение
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Решение
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Деление десятичных дробей
Пусть хотя бы одно из чисел 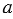
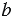
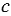
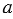
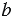
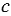
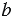
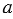
Рассмотрим деление десятичной дроби на натуральное число:
Пример 1: Найдём частное 143,64 : 4.
Выполним данный пример, используя деление уголком, не обращая внимания на запятую:
| — | 1 | 4 | 3 | 6 | 4 | 4 |
| 1 | 2 | 3 | 5 | 9 | 1 | |
| — | 2 | 3 | ||||
| 2 | 0 | |||||
| — | 3 | 6 | ||||
| 3 | 6 | |||||
| — | 4 | |||||
| 4 | ||||||
| 0 |
Чтобы разделить десятичную дробь на натуральное число, нужно:
1) разделить дробь на это число, не обращая внимания на запятую;
2) поставить в частном запятую, когда кончится деление целой части.
Мы рассмотрели пример, когда целая часть делимого больше делителя, если целая часть делимого меньше делителя, то целая часть частного будет равна нулю.
Пример 2: Найдём частное 5,418 : 14.
| — | 5 | 4 | 1 | 8 | 1 | 4 |
| 4 | 2 | 0 | 3 | 8 | 7 | |
| — | 1 | 2 | 1 | |||
| 1 | 1 | 2 | ||||
| — | 9 | 8 | ||||
| 9 | 8 | |||||
| 0 |
Пример 3: Найдём частное 0,4488 : 12.
| — | 0 | 4 | 4 | 8 | 8 | 1 | 2 |
| 3 | 6 | 0 | 0 | 3 | 7 | 4 | |
| — | 8 | 8 | |||||
| 8 | 4 | ||||||
| — | 4 | 8 | |||||
| 4 | 8 | ||||||
| 0 |
Пример 4: Найдём частное 32,86 : 5.
| — | 3 | 2 | 8 | 6 | 5 |
| 3 | 0 | 6 | 5 | 7 | |
| — | 2 | 8 | |||
| 2 | 5 | ||||
| — | 3 | 6 | |||
| 3 | 5 | ||||
| 1 |
Мы видим, что цифры в делимом закончились, но при этом остаток не равен 0. То есть деление не окончено. В таких случаях пользуемся тем, что, если приписать справа от десятичной дроби сколько угодно нулей, дробь не изменится, а, значит, числа делителя не могут закончиться. Тогда получаем:
| — | 3 | 2 | 8 | 6 | 5 |
| 3 | 0 | 6 | 5 | 7 | 2 |
| — | 2 | 8 | |||
| 2 | 5 | ||||
| — | 3 | 6 | |||
| 3 | 5 | ||||
| — | 1 | 0 | |||
| 1 | 0 | ||||
| 0 |
Мы знаем, что одно натуральное число не всегда делится на другое нацело. Рассмотрим такой пример.
Пример 5: Найдем частное 37 : 2.
| — | 3 | 7 | 2 |
| 2 | 1 | 8 | |
| — | 1 | 7 | |
| 1 | 6 | ||
| 1 |
Мы видим, что цифры в делимом закончились, но при этом остаток не равен 0. То есть деление не окончено. Но нам известно, что любое натуральное число можно записать в виде десятичной дроби, поставив запятую после данного числа и после нее подписав необходимое количество нулей, тогда имеем:
| — | 3 | 7 | 0 | 2 |
| 2 | 1 | 8 | 5 | |
| — | 1 | 7 | ||
| 1 | 6 | |||
| — | 1 | 0 | ||
| 1 | 0 | |||
| 0 |
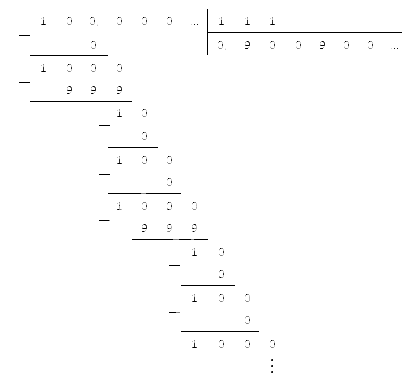
Пример 6: Найдём частное 1 : 160.
Делитель больше делимого, значит, в частное записываем 0, затем ставим запятую. Нам известно, что любое натуральное число можно записать в виде десятичной дроби, поставив запятую после данного числа и после нее подписав необходимое количество нулей, записываем в делимом 0, получаем:
10 меньше 160, значит, в частное записываем 0 и дописываем 0 в делителе, получаем:
| — | 1 | 0 | 0 | 1 | 6 | 0 |
| 0 | 0 | 0 |
100 меньше 160, значит, в частное записываем 0 и дописываем 0 в делителе, получаем:
| — | 1 | 0 | 0 | 0 | 1 | 6 | 0 |
| 9 | 6 | 0 | 0 | 0 | 0 | 6 | |
| 4 | 0 |
| — | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 6 | 0 |
| 9 | 6 | 0 | 0 | 0 | 0 | 6 | 2 | 5 | |
| — | 4 | 0 | 0 | ||||||
| 3 | 2 | 0 | |||||||
| — | 8 | 0 | 0 | ||||||
| 8 | 0 | 0 | |||||||
| 0 |
Правило деления десятичных дробей на на 0,1; 0,01; 0,001 и т.д.:
| Чтобы разделить десятичную дробь на 0,1, 0,01, 0,001 и т. д., надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и т. д. цифры. |
Правило деления десятичных дробей на на 10; 100; 1 000 и т.д.:
| Чтобы разделить десятичную дробь на 10, 100, 1 000 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры. |
Зная это правило, можно следующий следующий вывод:
Если делимое и делитель увеличить одновременно в 10, 100, 1 000 и т. д. раз, то частное не изменится.
Пример 7: Найдем частное 14,364 : 0,4.
Увеличим делимое и делитель одновременно в 10 раз. Тогда получим: 14,364 : 0,4 = 143,64 : 4.
Деление десятичной дроби 143,64 на 4 у нас выполнено выше, значит, мы можем записать, что 14,364 : 0,4 = 143,64 : 4 = 35,91.
Правило деления десятичной дроби на десятичную дробь:
Чтобы разделить десятичную дробь на десятичную, нужно:
1) перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
2) выполнить деление на натуральное число.
Поделись с друзьями в социальных сетях:
Деление десятичных дробей: правила, примеры
В данной публикации мы рассмотрим, как десятичную дробь можно разделить на натуральное целое число или другую десятичную дробь. Также разберем примеры для закрепления изложенного материала.
Деление десятичной дроби на натуральное число
Делитель – 10, 100, 1000, 10000 и т.д.
Чтобы разделить десятичную дробь на натуральное число 10, 100, 1000, 10000 и т.д., выполняем перенос десятичного разделителя (запятой) влево на столько позиций, сколько нулей содержит делитель.
Пример 1
Объяснение: В числе 10 всего один ноль, значит запятую сдвигаем на одну позицию влево.
Пример 2
Объяснение: В числе 100 два нуля, значит запятую сдвигаем на две позиции.
Примечание: если количество нулей в делителе больше количества цифр в целой части делимого, значит отсчитываем столько позиций, сколько позволяет дробь, затем дописываем оставшееся количество нулей слева, ставим запятую и добавляем ноль в целой части новой десятичной дроби.
Пример 3
62,75 : 1000 = 0,06275
Объяснение: Т.к. в числе 1000 три нуля, отсчитываем две позиции влево, добавляем оставшийся ноль с левой стороны, пишем запятую и затем – ноль в целой части полученной дроби.
Делитель – любое число
Чтобы разделить десятичную дробь на любое натуральное целое число:
Пример 4: разделим дробь 12,516 на 3.
Пример 5: разделим дробь 3,726 на 15.
Т.к. целая часть исходной дроби меньше делителя, значит целая часть частного равняется 0 (т.е. пишем ноль, ставим запятую и продолжаем выполнять деление).
Деление десятичной дроби на другую десятичную дробь
Чтобы разделить одну десятичную дробь на другую, умножаем обе дроби на такое число (10, 100, 1000 и т.д.), чтобы они стали целыми числами (количество нулей у множителя зависит от наибольшего количества цифр после запятой у той или иной дроби). Затем находим частное.
Примечание: этот же прием можно применять, чтобы разделить десятичную дробь на целое число.
Пример 6: найдем, сколько будет 5,468 делить на 3,2.
У дроби 5,468 три цифры после запятой, а у 3,2 – всего одна. Значит их обе умножаем на 1000, затем находим требуемый результат.
Урок 45 Бесплатно Деление десятичных дробей
На этом уроке мы продолжим изучать десятичные дроби и математические действия с ними.
Сегодня речь пойдет о делении десятичных дробей.
Сформулируем правило деления десятичной дроби на натуральное число.
Научимся делить натуральные числа без остатка.
Рассмотрим быстрый и удобный способ деления десятичной дроби на 10, 100, 1000 и т.д.
Применим полученные знания при решении различных задач.
Деление десятичной дроби на натуральное число
Решим простую задачу на деление.
15,3 литра компота разлили поровну в 5 банок.
Сколько литров компота налили в каждую банку?
Запишем кратко условие задачи.
В 5 банках- 15,3 л компота.
В 1 банке- ? л компота.
Так как в каждую банку налили одинаковое количество компота, то, узнав сколько литров компота налили в одну банку, определим сколько компота находится в каждой банке.
Чтобы узнать сколько литров компота в одной банке, необходимо общий объем компота разделить на количество банок, в которые его разлили.
Разделим десятичную дробь 15,3 на 5.
Что значит разделить десятичную дробь на натуральное число?
Разделить десятичную дробь на натуральное число- это значит найти такую дробь, которая при умножении на это натуральное число дает делимое.
Рассмотрим правило деления десятичной дроби на натуральное число столбиком (уголком).
Деление десятичной дроби практически не отличается от умножения натуральных чисел, главное правильно определить место десятичной запятой в полученном частном.
Чтобы разделить десятичную дробь на натуральное число необходимо:
Используя данный алгоритм, разделим 15,3 на 5.
Для нашей задачи получаем:
Начнем деление с целой части десятичной дроби.
Выберем в делимом наименьшее неполное делимое, которое делится на 5— это число 15.
Разделим неполное делимое на делитель.
Разделим 15 на 5, получится число 3 запишем его в частное.
Деление целой части закончено (в целой части знаков больше нет), поставим десятичную запятую в частном.
Найдем остаток от промежуточного деления: вычтем из неполного делимого произведение делителя и найденного неполного частного.
Получим: 15 – (5 ∙ 3) = 15 – 15 = 0
Остаток от деления получился равным нулю.
Далее мы будем делить дробную часть десятичной дроби, не обращая внимание на десятичную запятую.
Сносим число 3, но так как 3 на 5 не делится, в частное после десятичной запятой запишем нуль.
Чтобы дальше продолжить деление, необходимо в делимом справа дописать дополнительный один нуль (это действие не изменит дробь), а затем этот нуль снесем к тройке.
Получим следующее промежуточное делимое- это число 30.
Разделим 30 на делитель 5, в частном получим 6 сотых долей.
Найдем остаток от промежуточного деления.
30 – (5 ∙ 6) = 30 – 30 = 0
В остатке получили нуль, в делимом знаков больше нет, деление закончено.
В итоге получаем: 15,3 ÷ 5 = 3,06 (л) компота налили в каждую банку.
Ответ: 3,06 (л).
Могут возникнуть случаи, когда целая часть делимого меньше делителя или равна нулю.
У меня есть дополнительная информация к этой части урока!
Решим простую задачу.
Кусок ленты длиной 2,4 м разделили на 4 равные части.
Определите, какова длина каждой части.
Ленту разрезали на одинаковые части, следовательно, если найдем длину одной части, станет известна длина каждой части.
Разделим десятичную дробь 2,4 на 4 уголком.
Начнем деление с целой части десятичной дроби.
В целой части делимого стоит число 2.
Число 2 на 4 не делится записываем в частное нуль целых и ставим десятичную запятую, так как деление целой части десятичной дроби на этом закончено.
Определим остаток от промежуточного деления: 2 – (4 ∙ 0) = 2 – 0 = 2.
Продолжаем деление, к остатку сносим 4 десятых, образуется неполное делимое 24.
Неполное делимое 24 разделим на делитель 4, получаем число 6, запишем его в частное после запятой.
Найдем остаток от промежуточного деления: 24 – (4 ∙ 6) = 24 – 24 = 0.
В остатке получили нуль, в делимом знаков больше нет, деление закончено.
В результате получаем: 2,4 ÷ 4 = 0,6 (м) длина каждой части ленты.
Ответ: 0,6 (м).
Пройти тест и получить оценку можно после входа или регистрации
Деление натуральных чисел без остатка
На одном из уроков мы выяснили, что любая обыкновенная дробь (правильная и неправильная)- это ничто иное, как математическая операция деления.
С помощью обыкновенной дроби можно записать частное любых двух натуральных чисел.
\(\mathbf<\frac
Рассмотрим простой пример.
Для гостей разрезали пирог на шесть равных частей.
Каждый гость съел по кусочку, в результате пирог закончился, не осталось ни одного куска.
В таком случае дробь \(\mathbf<\frac<6><6>>\) будет показывать, что целое (весь пирог) разделили на шесть равных частей, а потом все эти шесть частей съели.
В любой обыкновенной дроби дробная черта означает знак деления, получаем:
Так как в нашем примере делимое (числитель) равно делителю (знаменателю), получаем:
Что представляет собой неправильная обыкновенная дробь нам тоже хорошо известно.
Числитель в неправильной дроби всегда больше знаменателя.
Семиметровую ленту разрезали на 5 равных частей.
Определите какова длина каждой части.
Чтобы узнать длину каждой части, необходимо длину всей ленты разделить на 5.
Разделим столбиком (уголком) 7 на 5.
Выделим в делимом наименьшее неполное делимое, которое делится на 5.
В нашем случае это само число 7.
Разделим неполное делимое на делитель.
Разделим 7 на 5 получим 1— это неполное частное.
Найдем остаток от промежуточного деления: вычтем из делимого произведение делителя и неполного частного.
7 – (5 ∙ 1) = 7 – 5 = 2.
Получим в остатке число 2.
Раньше на данном этапе мы бы остановили процесс деления.
Но сейчас деление мы можем довести до конца, т.е. разделить 7 на 5 без остатка.
Для этого необходимо разделить 2 единицы, оставшиеся в остатке, на 5 частей.
После того, как мы нашли целую часть (т.е. деление целых частей закончили), в частном после единицы поставим десятичную запятую и приступим к нахождению дробной части.
Чтобы продолжить деление, необходимо делимое натуральное число представить в виде десятичной дроби: в делимом справа поставить десятичную запятую, после запятой дописать один нуль (это действие не изменит число), а затем этот нуль снести к остатку.
Получаем следующее промежуточное делимое- это число 20.
Теперь число 20 легко разделить на делитель 5.
20 ÷ 5 = 4
Запишем полученное число 4 в частное после десятичной запятой.
Умножим делитель на найденное число 4.
5 ∙ 4 = 20
Произведение запишем под неполным делимым.
Найдем остаток от промежуточного деления: 20 – (5 ∙ 4) = 20 – 20 = 0.
Получим в остатке нуль, в делимом знаков больше нет, а это значит деление столбиком завершено.
В итоге получим следующий результат: 7 ÷ 5 = 1,4 (м) длина каждой части ленты.
Ответ: 1,4 (м).
В таком случае делимое (числитель) меньше делителя (знаменателя).
Два друга поровну поделили апельсин, разрезав его на две части.
Определим сколько апельсина достанется каждому из друзей?
Такую простую задачу мы решали не один раз.
Один апельсин, поделенный на две части, можно представить в виде правильной обыкновенной дроби.
½ апельсина достанется каждому из друзей.
Однако, зная, что дробная черта- это знак деления, разделим единицу на 2.
Выполним деление уголком.
Выделим в делимом наименьшее неполное делимое, которое делится на 2.
В нашем случае такое число отсутствует.
Невозможно 1 разделить на 2, поэтому в частное запишем нуль и поставим десятичную запятую.
Умножим делитель 2 на неполное частное 0.
2 ∙ 0 = 0
Запишем полученное произведение под делимым, вычитанием найдем остаток.
Чтобы продолжить деление, необходимо делимое натуральное число представить в виде десятичной дроби: в делимом справа поставить десятичную запятую, после запятой дописать один нуль (это действие не изменит число), а затем этот нуль снести к остатку.
Получаем промежуточное делимое- это число 10.
Приступим к нахождению дробной части.
Для этого 10 разделим на 2.
10 ÷ 2 = 5
Запишем полученное число 5 в частное после запятой.
Умножим делитель на найденное число 5.
2 ∙ 5 = 10
Произведение запишем под неполным делимым.
Найдем остаток от промежуточного деления: 20 – (5 ∙ 4) = 20 – 20 = 0.
Получим в остатке нуль, в делимом знаков больше нет, а это значит деление столбиком 1 на 2 можно считать завершенным.
В итоге получим следующий результат: 1 ÷ 2 = 0,5 (ап.) получит каждый из друзей.
Ответ: 0,5 (ап.).
У меня есть дополнительная информация к этой части урока!
Если разделить целый апельсин на две части, каждая из которых равна ½ = 0,5 и снова их сложить в единое целое, то можно получить тот самый один апельсин.
Проверим данное утверждение:
Выполним сложение двух десятичных дробей по правилам сложения столбиком натуральных чисел, не обращая внимание на десятичные запятые.
Сложим цифры поразрядно.
Нуль, стоящий после десятичной запятой, можно отбросить, получаем:
0,5 + 0,5 = 1 (апельсин)
Пройти тест и получить оценку можно после входа или регистрации
Правило деления десятичной дроби на 10, 100, 1000 и т.д.
Выясним, как легко и быстро разделить десятичную дробь на 10, 100, 1000 и т.д.
Для того чтобы сформулировать правило деления десятичной дроби на 10, 100, 1000 и т.д., рассмотрим три примера.
Пример №1.
Выразим в метрах длину 834,5 дециметров.
Один дециметр в 10 раз меньше метра, следовательно, чтобы перевести величину из дециметров в метры, необходимо количество дециметров разделить на 10.
Разделим десятичную дробь 834,5 на 10 столбиком.
Начнем деление с целой части десятичной дроби.
Выделим в делимом неполное делимое.
Выберем наименьшее число, которое делится на 10- это число 83.
Разделим неполное делимое на делитель.
Разделим 83 на 10, получится число 8 запишем его в частное.
Найдем остаток от промежуточного деления: 83 – (10 ∙ 8) = 83 – 80 = 3.
Получим в остатке число 3.
Продолжим делить целую часть дробного числа 834,5.
К остатку от промежуточного деления сносим число 4.
Получаем следующее промежуточное делимое- это число 34.
Разделим 34 на делитель 10, в частном получим в разряде десятков число 3.
Найдем остаток от промежуточного деления: 34 – (10 ∙ 3) = 34 – 30 = 4.
Так как остаток 4 на 10 не делится, в целой части знаков больше нет, т.е. деление целой части дробного числа закончено, поставим десятичную запятую в частном.
Продолжим деление десятичной дроби 834,5 далее.
Выполним деление дробной части десятичной дроби по правилу деления уголком, как делят натуральные числа, не обращая внимание на десятичную запятую в делимом.
В итоге получаем: 834,5 дм = 834,5 ÷ 10 = 83,45 м.
Пример №2.
Выразим 834,5 сантиметров в метрах.
Один сантиметр в 100 раз меньше метра, следовательно, чтобы перевести величину из сантиметров в метры, необходимо количество сантиметров разделить на 100.
Разделим десятичную дробь 834,5 на 100 столбиком.
Начнем деление с целой части десятичной дроби.
Выделим в делимом неполное делимое.
Выберем наименьшее число, которое делится на 100- это число 834.
Разделим неполное делимое на делитель.
Разделим 834 на 100, получится число 8 запишем его в частное.
Найдем остаток от промежуточного деления: 834 – (10 ∙ 8) = 834 – 800 = 34.
Получим в остатке число 34.
Так как остаток 34 на 100 не делится, в целой части знаков больше нет, т.е. деление целой части дробного числа закончено, поставим десятичную запятую в частном.
Продолжим деление десятичной дроби 834,5 далее.
Выполним деление дробной части десятичной дроби по правилу деления уголком, как делят натуральные числа, не обращая внимание на десятичную запятую в делимом.
В результате получаем: 834,5 см = 834,5 ÷ 100 = 8,345 м.
Пример №3.
Выразим 834,5 миллиметров в метрах.
Один миллиметр в 1000 раз меньше метра, следовательно, чтобы перевести величину из миллиметров в метры, необходимо количество миллиметров разделить на 1000.
Разделим столбиком десятичную дробь 834,5 на 1000.
Чтобы разделить десятичную дробь 834,5 на 1000, необходимо разделить сначала целую часть этой десятичной дроби.
834 на 1000 не делится, записываем в частное нуль.
Деление целой части на этом закончено, следовательно, поставим в частное после нуля десятичную запятую и продолжим деление столбиком, как делят натуральные числа, не обращая внимание на десятичную запятую в делимом.
В результате получаем: 834,5 мм = 834,5 ÷ 1000 = 0,8345 м.
Обратим внимание на полученные равенства.
834,5 ÷ 10 = 83,45
834,5 ÷ 100 = 8,345
834,5 ÷ 1000 = 0,8345
Отметим некоторую закономерность: при делении десятичной дроби на 10, 100, 1000 набор цифр и порядок их следования остается неизменным, а десятичная запятая меняет свое положение в числе.
При уменьшении десятичной дроби в 10 раз, запятая переносится на один десятичный знак.
При уменьшении десятичной дроби в 100 раз, запятая переносится на два десятичных знака.
При уменьшении десятичной дроби в 1000 раз, запятая переносится на три десятичных знака.
Существует правило, которое позволяет легко и быстро разделить любую десятичную дробь на 10, 100, 1000 и т.д.
Правило: чтобы разделить любую десятичную дробь на 10, 100, 1000 и т.д., необходимо перенести в этой дроби запятую на столько знаков влево, сколько нулей стоит после единицы в делителе.
Умножим 123,4 на 1000, для этого нужно запятую перенести на три знака влево.
Однако, для переноса запятой влево не хватает цифр.
Если при делении десятичной дроби на 10, 100, 1000 и т.д. не хватает знаков для переноса запятой, то необходимо в этой дроби слева приписать столько нулей, сколько требуется (данное действие не изменит заданную десятичную дробь).
В нашем случае добавим слева один нуль.
Только после этого перенесем запятую влево на три цифры.
Решим несколько простых задач.
Задача №1.
За 10 килограммов картофеля заплатили 564 рубля.
Сколько стоит один килограмм картофеля?
У меня есть дополнительная информация к этой части урока!
Для решения данной задачи вспомним, что такое цена, количество, стоимость.
Цена- это величина, которая показывает сколько стоит одна единица товара, измеряется в денежных единицах.
Количество- число, которое показывает сколько купили единиц товара, измеряется в штуках, кг, м, л и т.д.
Стоимость- это величина, которая показывает сколько денег потрачено на всю покупку, измеряется в денежных единицах.
Чтобы найти стоимость покупки, необходимо цену товара умножить на количество этого товара.
Формула для определения стоимости выглядит так:
С— стоимость
а— цена за единицу товара
n— количество товара
Задача №2.
15800 метров поезд двигался со скоростью 100 км/ч.
За какое время он прошел этот участок пути?
Ответ запишите в минутах.
У меня есть дополнительная информация к этой части урока!
Переведем 15800 метров в километры.
В 1 км = 1000 м, значит один метр меньше километра в 1000 раз.
Чтобы перевести величину из метров в километры, необходимо заданное количество метров разделить на 1000.
Разделим 15800 на 1000.
Представим натуральное число 15800 в виде десятичной дроби.
Для этого в конце числа поставим десятичную запятую, а после запятой припишем нуль.
Получим: 15800,0.
Найдем значение выражения 15800,0 ÷ 1000.
Чтобы разделить десятичную дробь на 1000, необходимо перенести в этой дроби десятичную запятую на три знака влево.
По условию известны следующие величины:
S— пройденный путь.
V— скорость движения автомобиля.
Неизвестно t— время движения.
Решение данной задачи будет выглядеть так.
Задача №3.
Маша загадала число.
Если это число увеличить в 1000 раз, то получится 2345,6.
Какое число загадала Маша?
Пусть х— это число, которое загадала Маша.
При увеличении задуманного числа в 1000 раз, получится выражение х ∙ 1000.
Зная, что в результате получится число 2345,6 составим уравнение.
х ∙ 1000 = 2345,6
Получили простое уравнение, в котором неизвестен множитель.
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
х ∙ 1000 = 2345,6
х = 2345,6 ÷ 1000
Чтобы разделить десятичную дробь на 1000, необходимо перенести в этой дроби десятичную запятую на три знака влево.
х = 2,3456
Ответ: число 2,3456 задумала Маша.
Пройти тест и получить оценку можно после входа или регистрации