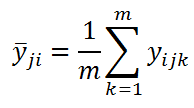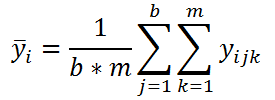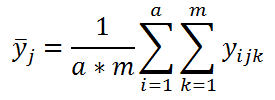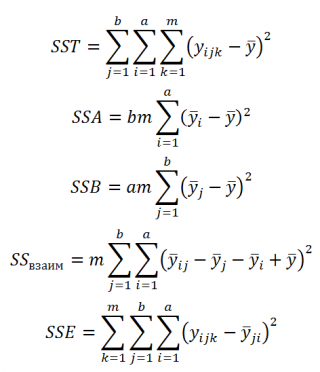Как сделать дисперсионный анализ в excel
Однофакторный дисперсионный анализ в Excel
Однофакторный дисперсионный анализ изучает влияния одного фактора на анализируемый признак.
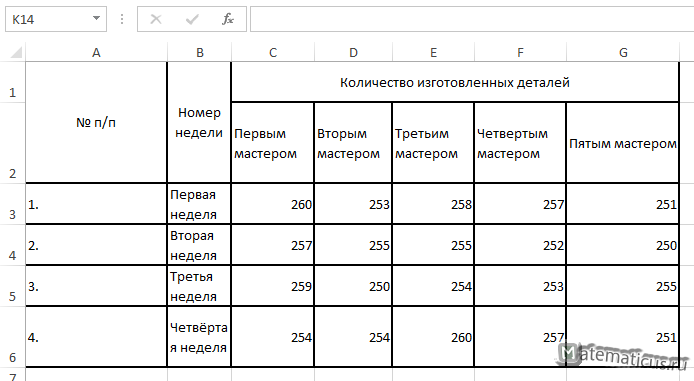
В таблицы приведены статистические данные по количеству изготовленных деталей на заводе каждым мастером в течение каждой недели.
Необходимо выяснить зависимость количества изготовленных деталей от производительности мастера. Уровень значимости равен α=0.05.
| № п/п | Номер недели | Количество изготовленных деталей | ||||
| Первым мастером | Вторым мастером | Третьим мастером | Четвертым мастером | Пятым мастером | ||
| 1. | Первая неделя | 260 | 253 | 258 | 257 | 251 |
| 2. | Вторая неделя | 257 | 255 | 255 | 252 | 250 |
| 3. | Третья неделя | 259 | 250 | 254 | 253 | 255 |
| 4. | Четвёртая неделя | 254 | 254 | 260 | 257 | 251 |
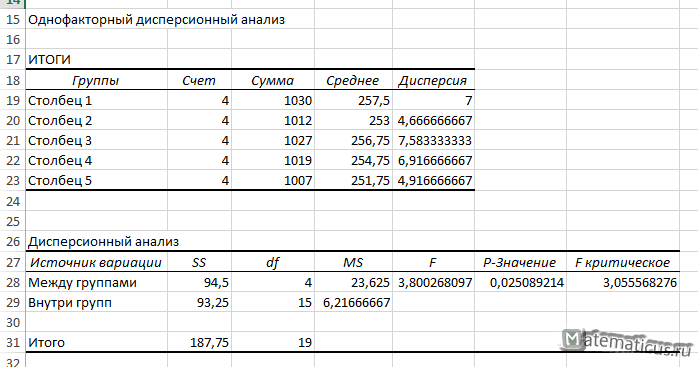
В результате получим решение в виде таблицы.
| Однофакторный дисперсионный анализ | ||||||
| ИТОГИ | ||||||
| Группы | Счет | Сумма | Среднее | Дисперсия | ||
| Столбец 1 | 4 | 1030 | 257,5 | 7 | ||
| Столбец 2 | 4 | 1012 | 253 | 4,666666667 | ||
| Столбец 3 | 4 | 1027 | 256,75 | 7,583333333 | ||
| Столбец 4 | 4 | 1019 | 254,75 | 6,916666667 | ||
| Столбец 5 | 4 | 1007 | 251,75 | 4,916666667 | ||
| Дисперсионный анализ | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Между группами | 94,5 | 4 | 23,625 | 3,800268097 | 0,025089214 | 3,055568276 |
| Внутри групп | 93,25 | 15 | 6,21666667 | |||
| Итого | 187,75 | 19 | ||||
Из таблицы значения F-критерия равно Fнабл=3.8, а Fкрит=3, правосторонний интервал (3; +∞) Fнабл>Fкрит, отсюда следует, что Fнабл лежит в этом интервале, следовательно, нулевую гипотезу H0 о равенстве групповых матожиданий — отвергаем, следовательно фактор — количества изготовленных деталей зависит от признака — производительности мастера.
Найдём выборочный коэффициент детерминации:
Этот показатель говорит о том, что около половины еженедельного количества изготовленных деталей мастерами связано с номером недели.
Двухфакторный дисперсионный анализ в EXCEL
Пусть имеется случайная переменная Y , значения которой мы можем измерять. Исследователь предполагает, что эта переменная зависит от 2-х факторов, значения которых мы можем контролировать, т.е. задавать с требуемой точностью. Покажем как методом дисперсионного анализа проверить гипотезу о наличии или отсутствии влияния указанных факторов на зависимую переменную Y .
В этой статье рассмотрим метод дисперсионного анализа в случае двух факторов (Фактор А и Фактор В) (Two Factor ANOVA with Replication).
Обозначения
Отдельные, заданные значения каждого фактора называются уровнями ( levels ) или испытаниями ( treatments ).
Предполагается, что дисперсии всех выборок σ 2 неизвестны, но равны между собой.
Рассмотрим двухфакторный дисперсионный анализ при решении задачи.
Задача
В компании, изготавливающей изделия путем механообработки, необходимо исследовать влияние на качество изделия двух факторов: Метода обработки поверхности детали, и Исходного материала детали (используется сталь с различным легированием).
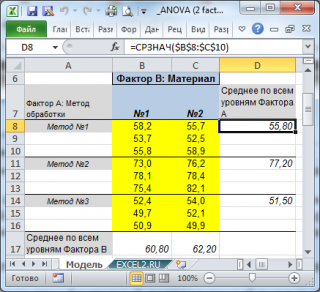
Другими словами мы имеем 6 выборок по 3 значения в каждой. Средние этих выборок для каждой комбинации факторов ij можно вычислить по формуле:
Также для дальнейших вычислений нам потребуется вычислить еще несколько средних значений. Во-первых, вычислим среднее всех измерений, относящихся к каждому уровню i Фактора А:
Во-вторых, вычислим среднее всех измерений, относящихся к каждому уровню j Фактора В:
Взаимодействие факторов
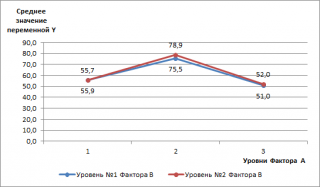
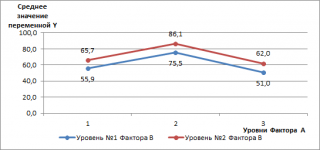
Как видно из диаграммы – синяя и красная линии практически параллельны друг другу. Это означает, что взаимодействие между факторами практически отсутствует (они не влияют друг на друга). Действительно, выбор метода обработки никак не может влиять на выбор конкретного исходного материала.
Вот еще одна диаграмма, демонстрирующая независимость 2-х факторов.
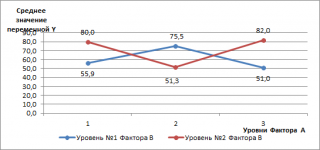
Обратная ситуация показана на диаграмме ниже, когда оба фактора взаимодействуют.
Из этой диаграммы видно, что при уровне №1 фактора В (синяя линия) количество дефектов сначала возрастает, затем снижается (когда мы переходим от метода №1 к №2, затем к №3). Мы наблюдаем диаметрально противоположную ситуацию при уровне №2 фактора В (красная линия): количество дефектов сначала снижается, а затем возрастает. В этом случае говорят о наличии взаимодействия факторов.
Возвращаемся к диаграммам взаимодействия. Очевидно, что делать заключение о наличии или отсутствии взаимодействия факторов невозможно лишь по взаимному расположению линий на диаграмме. Для формулирования утверждения о взаимодействии требуется составить математическое выражение. Это выражение должно вычисляться на основании исходных данных, а результат должен сравниваться с неким критическим значением. Займемся этим в следующем разделе.
Определяем причины изменчивости исходных данных
По аналогии с однофакторным дисперсионным анализом общую изменчивость (разброс) значений Y относительно общего среднего (SST = Sum of Squares Total, общая сумма квадратов) определим как сумму нескольких компонентов, в данном случае 4-х:
SST=SSA+SSB+ SS взаим +SSE
SST и все 4 компонента вычисляются на основании имеющихся исходных данных:
Также в дисперсионном анализе используется понятие среднего квадрата отклонений (Mean Square) или сокращенно MS. Соответственно для SST имеем MST=SST/(N-1), где N= a*b*m является общим количеством измерений (18). Для других SS степени свободы приведены в таблице ниже.
Таким образом, MS имеет смысл средней изменчивости на 1 наблюдение (с некоторой поправкой). Эта поправка отражает тот факт, что MS должна вычисляться не делением SS на соответствующее количество наблюдений, а делением на число степеней свободы (degrees of freedom, DF). Например, чтобы вычислить MST, мы из N (общего количества наблюдений) должны вычесть 1, т.к. в выражении SST присутствует одно (1) среднее значение (аналогично тому, как мы делали при вычислении дисперсии ).
Сначала тестируют гипотезу об отсутствии взаимодействия между факторами. Мы можем отклонить Н 0 взаим в пользу Н 1взаим при заданном уровне значимости α (альфа), если вычисленное значение тестовой статистики F= MS взаим /MSE больше F критич альфа – значения случайной величины F имеющей распределение Фишера с (b-1)*(a-1) и a*b*(m-1) степенями свободы.
Вычисления в MS EXCEL
В файле примера приведено решение вышеуказанной задачи: вычислены средние значения выборок, суммы квадратов (SS), степеней свобод, средние квадратов отклонений (MS).
Для вычислений критических значений в MS EXCEL имеется специальная функция = F.ОБР.ПХ()
Формула для вычисления F 1критич = F.ОБР.ПХ(a-1; a*b*(m-1);альфа)
В MS EXCEL первое p -значение (вероятность того, что случайная величина F 1 = MSА/MSE примет значение более F 01 ) можно вычислить по формуле:
= F.РАСП.ПХ((MSА/MSE; a-1; a*b*(m-1))
Второе p -значение (вероятность того, что случайная величина F 2 = MSВ/MSE примет значение более F 0 2 ) вычисляется по аналогичным формулам.
В нашей задаче p -значения получились 0,000 и 0,253, что значительно меньше обычно принимаемого в качестве уровня значимости 0,05. Таким образом, обе нулевых гипотезы отклоняются.
Как сделать дисперсионный анализ в excel
п.15. Решение прикладных задач средствами EXCEL .
Однофакторный дисперсионный анализ
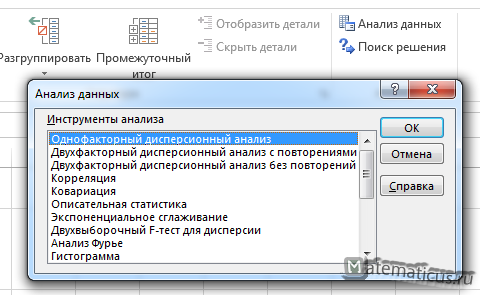
В MS Excel для проведения однофакторного дисперсионного анализа используется процедура Однофакторный дисперсионный анализ.
Для проведения дисперсионного анализа необходимо:
•ввести данные в таблицу, так чтобы в каждом столбце оказались данные, соответствующие одному значению исследуемого фактора, а столбцы располагались в порядке возрастания (убывания) величины исследуемого фактора,
•выполнить команду Сервис > Анализ данных;
•в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать процедуру Однофакторный дисперсионный анализ, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку ОК;
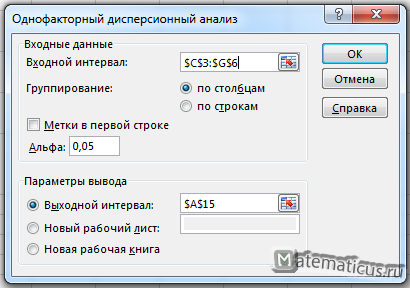
•в появившемся диалоговом окне задать Входной интервал, то есть ввести ссылку на диапазон анализируемых данных, содержащий все столбцы данных. Для этого следует навести указатель мыши на верхнюю левую ячейку диапазона данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
•в разделе Группировка переключатель установить в положение по столбцам;
•указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.
Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа: средние, дисперсии, критерий Фишера и другие показатели.
Интерпретация результатов. Влияние исследуемого фактора определяется по величине значимости критерия Фишера, которая находится в таблице Дисперсионный анализ на пересечении строки Между группами и столбца Р-Значение. В случаях, когда Р-Значение
Изучалось различие в продуктивности воспроизведения одного и того же материала трех групп испытуемых (по 5 человек), различающихся условиями предъявления этого материала для запоминания. Результаты обследования приведены в таблице.