Как сделать доска гальтона
Доска гальтона своими руками
Как обычно гуглил по теме (делаю это периодически, вдруг чего нового нагуглица), и нашёл одно видео (ниже будет), а с него вышел на сайт, а с сайта вышел на замечательную галерею конструкций досок Гальтона (заинтересовавшимся рекомендую после прочтения поста пройтись по ссылкам). Итак, машины:
Эх, было бы у меня такое финансирование, как при создании такой машины, то я бы создал множество таких и ещё лучше и интереснее машин!
Следующая машина ахренительна тем, что имеет в своём составе счётчик падающих шариков, что весьма показательно для оценки флуктуаций.
Ну и ещё несколько девайсов:
Остальное можно поглядеть у них в альбоме.
Ну и собственно говоря завораживающее видео работы этой чудесной машины.
З.Ы. По ссылке, которую я уже давал выше есть ещё несколько интересных видео их работы.
Все ли видели волшебное видео о том, как каждый цвет имеет свою частоту и сталкиваясь с кристаллами кварца каждый цвет попадает только в свою ячейку?
Это видео конечно же фэйк – все шары в видео изначально белые, им назначен цвет уже в компьютерной обработке в зависимости от того в какой ячейке они были в конце.
Но вот само использованное устройство довольно примечательно. Это вариация доски Гальтона, и в нем кроется настоящая магия.
Galton box, также распространены названия квинкункс, quincunx и bean machine) — устройство, изобретённое английским учёным Фрэнсисом Гальтоном (первый экземпляр изготовлен в 1873 году, затем устройство было описано Гальтоном в книге Natural inheritance, изданной в 1889 году) и предназначающееся для демонстрации центральной предельной теоремы, нормального (гауссова) распределения.
В идеальном случае сталкиваясь со штырьком, шарик каждый раз с одинаковой вероятностью может повернуть либо направо, либо налево. Нижняя часть ящика разделена перегородками (число которых равно числу штырьков в нижнем ряду), в результате чего шарики, скатываясь на дно ящика, образуют столбики, которые тем выше, чем ближе к середине доски (при достаточно большом числе шариков внешний вид столбиков приближается к кривой нормального распределения).
Если нарисовать на задней стенке треугольник Паскаля, то можно увидеть, сколькими путями можно добраться до каждого из штырьков (чем ближе штырёк к центру, тем больше число путей).
В некоторых настольных играх, а также игровом автомате Патинко, используется доска Гальтона или схожие с ней устройства.
Устройство
Доска Гальтона представляет собой ящик с прозрачной передней стенкой. В заднюю стенку в шахматном порядке вбиты штырьки, образующие треугольник. Сверху в ящик через воронку (выход из которой расположен ровно посередине между левой и правой стенками) кидаются шарики. В идеальном случае сталкиваясь со штырьком, шарик каждый раз с одинаковой вероятностью может повернуть либо направо, либо налево. Нижняя часть ящика разделена перегородками (число которых равно числу штырьков в нижнем ряду), в результате чего шарики, скатываясь на дно ящика, образуют столбики, которые тем выше, чем ближе к середине доски (при достаточно большом числе шариков внешний вид столбиков приближается к кривой нормального распределения).
Если нарисовать на задней стенке треугольник Паскаля, то можно увидеть, сколькими путями можно добраться до каждого из штырьков (чем ближе штырёк к центру, тем больше число путей).
В некоторых настольных играх, а также игровом автомате Патинко, используется доска Гальтона или схожие с ней устройства.
Распределение шариков
Примечания
Ссылки
Вероя́тность — степень (относительная мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — маловероятным или невероятным. Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей либо меньшей. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднительна. Возможны различные градации «уровней» вероятности.
Исследование вероятности с математической точки зрения составляет особую дисциплину — теорию вероятностей. В теории вероятностей и математической статистике понятие вероятности формализуется как числовая характеристика события — вероятностная мера (или её значение) — мера на множестве событий (подмножеств множества элементарных событий), принимающая значения от 0 
до 1 . Значение 1 соответствует достоверному событию. Невозможное событие имеет вероятность 0 (обратное вообще говоря не всегда верно). Если вероятность наступления события равна p , то вероятность его ненаступления равна 1 − p . В частности, вероятность 1 / 2 означает равную вероятность наступления и ненаступления события.
Классическое определение вероятности основано на понятии равновозможности исходов. В качестве вероятности выступает отношение количества исходов, благоприятствующих данному событию, к общему числу равновозможных исходов. Например, вероятность выпадения «орла» или «решки» при случайном подбрасывании монетки равна 1/2, если предполагается, что только эти две возможности имеют место и они являются равновозможными. Данное классическое «определение» вероятности можно обобщить на случай бесконечного количества возможных значений — например, если некоторое событие может произойти с равной вероятностью в любой точке (количество точек бесконечно) некоторой ограниченной области пространства (плоскости), то вероятность того, что оно произойдёт в некоторой части этой допустимой области равна отношению объёма (площади) этой части к объёму (площади) области всех возможных точек.
Эмпирическое «определение» вероятности связано с частотой наступления события исходя из того, что при достаточно большом числе испытаний частота должна стремиться к объективной степени возможности этого события. В современном изложении теории вероятностей вероятность определяется аксиоматически, как частный случай абстрактной теории меры множества. Тем не менее, связующим звеном между абстрактной мерой и вероятностью, выражающей степень возможности наступления события, является именно частота его наблюдения.
Вероятностное описание тех или иных явлений получило широкое распространение в современной науке, в частности в эконометрике, статистической физике макроскопических (термодинамических) систем, где даже в случае классического детерминированного описания движения частиц детерминированное описание всей системы частиц не представляется практически возможным и целесообразным. В квантовой физике сами описываемые процессы имеют вероятностную природу.
Гальтон, Галтон, Голтон (англ. Galton) — имя собственное; распространено в виде фамилий.
Гальтон, Дороти (1901—1992) — британка, подозревавшаяся британскими спецслужбами в шпионстве на русских (однако доказано это никогда не было).
Галтон, Питер (род. 1942) — американский палеонтолог.
Гальтон, Фрэнсис (1822—1911) — английский исследователь, географ, антрополог и психолог; основатель дифференциальной психологии и психометрики, статистик.
Голтон, Лия (род. 1994) — английская футболистка.
Сэр Фрэ́нсис Га́льтон (Го́лтон; англ. Francis Galton; 16 февраля 1822 — 17 января 1911) — английский исследователь, географ, антрополог и психолог; основатель дифференциальной психологии и психометрики, статистик. Родился в Бирмингеме, в Англии.
Дом занимательной науки — музей, открытый 15 октября 1935 года в Ленинграде с целью популяризации научных знаний среди детей и взрослых и закрытый 29 июня 1941 года, с началом Великой Отечественной войны.
Доска — профильная деталь из древесины для покрытия полов.
Иконная доска — традиционная основа под темперную живопись в иконном писании.
Доска — игровое поле в ряде настольных игр.
Доска для игры в нарды
Доска для игры в Сянци
Доска — наименование спортивных снарядов в ряде видов спорта.
Роликовая доска — Скейтборд.
Сноуборд (спортивный инвентарь)
Доска Гальтона — устройство, предназначающееся для демонстрации центральной предельной теоремы.
Доска Уиджи (на авианосце) — специальный двухуровневый стол.
Доска для плавания — приспособление для плавания.
Доска объявлений — место, на котором размещаются объявления.
Электронная доска объявлений
Виртуальная доска объявлений
Доска почёта — в Советском Союзе — стенд с именами и фотографиями передовиков производства.
Гладильная доска — портативный, складной стол с жаропрочной крышкой.
Классная доска — используемая в образовательных учреждениях поверхность.
Аспидная доска — письменная принадлежность в виде пластины из сланца, на которой некогда учились писать.
Доска для рисования маркерами — вид классной доски.
Интерактивная доска — сенсорный экран, работающий как часть системы, в которую также входят компьютер и проектор.
Мемориальная доска — плита, увековечивающая память о знаменитом человеке или событии.
Приборная доска — Вертикальная передняя панель транспортного средства.
Стиральная доска — приспособление для ручной стирки.
Разделочная доска — предмет кухонной утвари, предназначенный для нарезания, реже разрубания продуктов питания.
Чертёжная доска — приспособление для черчения.
Патинко (яп. パチンコ) — игровой автомат, представляющий собой промежуточную форму между денежным игровым автоматом и вертикальным пинболом, необычайно популярен в Японии.
Так как в Японии не разрешены казино, а тотализатор допускается исключительно на лошадиных скачках, велосипедных и лодочных гонках, игра в патинко пользуется большой популярностью: 15 млн японцев регулярно посещают около 16 тыс. залов патинко, и существует около 34 тыс. профессиональных игроков, прибыль некоторых из них достигает 3 тыс. долларов в месяц. Согласно заявлениям некоторых профессиональных игроков, их ежемесячный выигрыш достигает 100 тыс. долларов, но это представляется маловероятным[кому?].
На других языках
This page is based on a Wikipedia article written by authors (here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
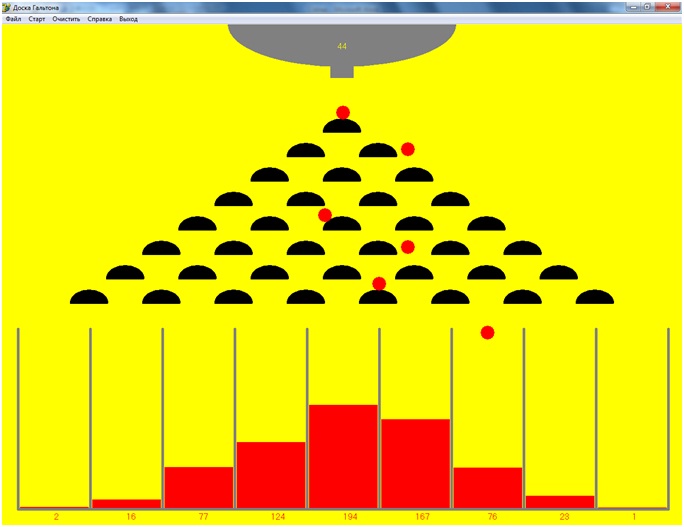
Доска Гальтона на Delphi 7
Доска Гальтона на Delphi 7
Изобразить на экране доску Гальтона с движущимися по ней шариками. Одновременно по доске должно двигаться несколько шариков. Использовать датчик случайных чисел для выбора пути шарика при прохождении через препятствие. Подсчитать число шариков, попавших в каждое из отделений.
Так или «примерно так» звучат задачи из этой серии….
Доска Гальтона (как в материальном, так и в виртуальном виде) при высокой точности изготовления (а умельцев, слава богу, во все времена хватало) демонстрирует «НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ» во всей его красе. Мы не знаем, как будет вести себя любой отдельный шар, но мы знаем, как будет себя вести «большое множество шаров».
Если взять тысячу шаров, то лишь единичные из них отклонятся от своей первоначальной траектории настолько, что попадут в боковые отсеки (полюса). Большая же часть ляжет в центральные карманы. Если один колышек сбивал их вправо, следующий направлял влево и так далее. Это явление называется «нормальным распределением» и широко используется в теории вероятностей.
Нормальное распределение – это такой же мощный закон, как, допустим, гравитационное притяжение. Даже наша жизнь очень напоминает доску Гальтона. Черная полоса в жизни, как правило, сменяется белой. Человека качает из стороны в сторону, но бьет не до смерти. Отдельные личности, конечно, становятся маргиналами-бомжами или, напротив, миллионерами. Но, сами знаете, большинство из нас, поободрав бока о житейские «препятствия», рано или поздно останавливаются в умеренной зоне (т.е. вдали от полюсов).
Ну, «теории» достаточно… Пора дробить поставленную задачу на части…
Раз на экране должны двигаться шары – значит не обойтись без мультипликации.
Раз будет мультипликация, значит, будут сменяющие друг друга, кадры.
Каждый очередной кадр должен показать шары с их новыми координатами (чуть ниже предыдущего местоположения, а правее или левее, как бог-случай даст).
Понятно, что воронка, упоры и стаканы, на всех кадрах – это МОНУМЕНТЫ. Поэтому их целесообразно поместить на отдельный bipmap, а каждый кадр получать, изображая нужные шары на копии этого фонового рисунка.
Сколько в воронке шаров я показываю только числом. Сколько шаров в каждом стакане – цифрами и пропорциональной величины прямоугольником красного цвета. А вот все движущиеся шары нужно прорисовывать конкретно. Так сколько же их будет? Какого размера массив создавать (под движущиеся шары)?
Безусловно, количество, одновременно движущихся шаров, зависит от количества стаканов (число которых, пусть задается пользователем). На единицу меньшим, чем количество стаканов, будет количество упоров в самом нижнем ряду. Да и количество рядов упоров будет таким же (на единицу меньшим, чем количество стаканов). Количество движущихся шаров целесообразно сделать меньше или равным количеству стаканов, допуская, что одновременно будет показываться шар над самым верхним упором или шар ниже последнего ряда упоров. Большее число одновременно движущихся шаров будет мешать зрительному восприятию траектории движения каждого отдельного шара.
const S_ARR=20; //максимальный размер массива движущихся шаров
Данные движущегося шара я храню (и изменяю) в записи-структуре:
Описание массивов:
var
glass:array of integer;
// массив стаканов (размерность устанавливает пользователь)
shar:array [0..S_ARR-1] of shpt;
//массив движущихся в настоящий момент шаров
Перебор всех движущихся шаров производится в процедуре-обработчике события таймера, формируя очередной кадр:
procedure TForm1.Timer1Timer(Sender: TObject);
var i:integer;
begin
inc(cou);
for i:=0 to m-1 do OneStepShar(shar[i]);
…
…
end;
где m – количество движущихся шаров в настоящий момент (в начале процесса растет от 0 до определенного числа, а после того как шары в воронке кончатся, начнет быстро убывать).
if hod=3 then
begin
hod:=0; inc(row);
if(random(1000)
И шар пойдет влево или вправо по воле случая в независимости от того, в какую сторону он двигался до этого.
Конечно, остаются еще некоторые вопросы (рабочие моменты), но Вы либо решите их самостоятельно, либо узнаете после тестирования ехе-шника, когда закажите код целиком (на любом, нужном Вам, языке программирования).