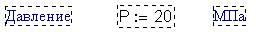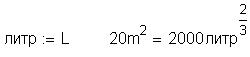Как сделать градусы в маткаде
Как сделать градусы в маткаде
Этот раздел описывает тригонометрические, гиперболические и показательные функции Mathcad вместе с обратными им. Здесь также описываются встроенные функции Бесселя.
Тригонометрические функции и обратные им.
Тригонометрические функции Mathcad и обратные им определены для любого комплексного аргумента. Они также возвращают комплексные значения везде, где необходимо. Результаты для комплексных значений вычисляются с использованием тождеств:
Для применения этих функций к каждому элементу вектора или матрицы используйте оператор векторизации.
Обратите внимание, что все эти тригонометрические функции используют аргумент, выраженный в радианах. Чтобы перейти к градусам, используется встроенная единица deg. Например, чтобы вычислить синус 45 градусов, введите sin(45*deg).
Имейте в виду, что из-за ошибок округления, свойственных машинной арифметике, Mathcad может возвращать очень большое число в той точке, где находится особенность вычисляемой функции. Вообще, необходимо быть осторожным при вычислениях в окрестности таких точек.
| asin(z) | Возвращает угол (в радианах), чей синус — z. |
| acos(z) | Возвращает угол (в радианах), чей косинус — z. |
| atan(z) | Возвращает угол (в радианах), чей тангенс — z. |
Гиперболические функции sinh и cosh определяются формулами:
Эти функции также могут использовать комплексный аргумент и возвращать комплексные значения. Гиперболические функции тесно связаны с тригонометрическими функциями. Справедливы формулы:
sinh(i


| sinh (z) | Возвращает гиперболический синус z. |
| cosh (z) | Возвращает гиперболический косинус z. |
| tanh (z) | Возвращает sinh(z)/cosh(z), гиперболический тангенс z. |
| csch (z) | Возвращает 1/sinh(z), гиперболический косеканс z. |
| sech (z) | Возвращает 1/cosh(z), гиперболический секанс z. |
| coth (z) | Возвращает 1/tanh(z), гиперболический котангенс z. |
| asinh (z) | Возвращает число, чей гиперболический синус — z. |
| acosh (z) | Возвращает число, чей гиперболический косинус — z. |
| atanh (z) | Возвращает число, чей гиперболический тангенс — z. |
Логарифмические и показательные функции
Логарифмические и показательные функции Mathcad могут использовать комплексный аргумент и возвращать комплексные значения. Значения экспоненциальной функции для комплексного аргумента вычисляются с применением формулы
e x+iy =e x (cos(y) + i
Вообще говоря, значения натурального логарифма даются формулой
ln(x + i





В Mathcad функция ln возвращает значение, соответствующее n = 0. А именно:
ln(x + i


Оно называется основным значением логарифма. Рисунок 1 иллюстрирует некоторые основные свойства логарифма.
| exp(z) | Возвращает e в степени z. |
| ln(z) | Возвращает натуральный логарифм z. (z 0). 0). |
| log(z) | Возвращает логарифм z по основанию 10. (z 0). 0). |
На Рисунке 1 показано, как можно использовать эти функции для вычисления логарифма по любому основанию.
Рисунок 1: Использование логарифмических функций.
Эти функции обычно возникают как решения для волнового уравнения, подчиненного цилиндрическим граничным условиям.
Функции Бесселя первого и второго рода, Jn(x) и Yn(x), являются решениями для дифференциального уравнения
Модифицированные функции Бесселя первого и второго рода, In(x) и Kn(x), являются решениями для немного видоизмененного уравнения:
| J0(x) | Возвращает J0(x); x вещественный. |
| J1(x) | Возвращает J1(x); x вещественный. |
| Jn(m, x) | Возвращает Jn(x); x вещественный, 0 m m 100. 100. |
| Y0(x) | Возвращает Y0(x); x вещественный, x > 0. |
| Y1(x) | Возвращает Y1(x); x вещественный, x > 0. |
| Yn(m, x) | Возвращает Yn(x). x > 0, 0 m m 100 100 |
| I0(x) | Возвращает I0(x); x вещественный. |
| I1(x) | Возвращает I1(x); x вещественный. |
| In(m, x) | Возвращает In(x); x вещественный, 0 m m 100. 100. |
| K0(x) | Возвращает K0(x); x вещественный, x > 0. |
| K1(x) | Возвращает K1(x); x вещественный, x > 0. |
| Kn(m, x) | Возвращает Kn(x). x > 0, 0 m m 100 100 |
Следующие функции возникают в широком круге задач.
x должен быть вещественным.
Гамма-функция Эйлера удовлетворяет рекуррентному соотношению
Откуда следует для положительных целых z:
Интеграл ошибок часто возникает в статистике. Он может также быть использован для определения дополнения интеграла ошибок по формуле:
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Как сделать градусы в маткаде
Физические величины в Mathcad
Три «школьных» анекдота в качестве эпиграфа:
1. Диалог в учительской:
Преподаватель Закона Божьего, обращаясь к физику: Сегодня ваш любимчик двойку получил. Спросил я его, что такое Божественная Сила. Так он мне ответил, что это произведение Божественной Массы на Божественное Ускорение.
Физик: Я ему и по физике двойку поставлю. Ведь произведение Божественной Массы на Божественное Ускорение дает Силу с Божественностью в квадрате, а не в первой степени.
2. Диалог на экзамене:
Преподаватель: Что такое лошадиная сила?
Ученик: Это сила, какую развивает лошадь ростом в один метр и весом в один килограмм.
Преподаватель: Да где ж вы такую лошадь видели?!
Ученик: А ее так просто не увидишь. Она хранится в Париже, в Палате мер и весов.
Архимед, Паскаль и Ньютон играют в прятки. Архимед водит и начинает считать. Паскаль убегает за горизонт, «в бесконечность», а Ньютон оглядывается, берёт палку, рисует вокруг себя квадрат со стороной 1 метр и становится внутрь квадрата. Архимед заканчивает считать, открывает глаза и видит Ньютона:
Архимед: Я вижу Ньютона!
Использование вычислительной техники в научно-технических расчетах сыграло с этими расчетами злую шутку: из расчетов были безжалостно выброшены размерности физических величин и единицы их измерения – метры, килограммы, секунды… Ручное решение физической задачи (школьной или вузовской задачи по физике, если говорить конкретнее), как правило, требовало и требует оперирования сугубо размерными величинами. Автоматизация таких расчетов – написание программ для компьютера исключает из задачи ее «физику»: переменные программы хранят только числовые величины, а соответствующие им единицы измерений программист должен «держать в уме». Из-за этого при переводе расчета на язык ЭВМ необходимо придерживаться строгого правила – все физические величины должны быть в одной системе единиц, кроме того, они должны быть без множителей мили, мега и т.д. Это жесткое правило вызывало и вызывает ряд неудобств, основные из которых следующие:
3. В создаваемые программы приходиться вставлять формулы, выведенные не только в результате теоретического анализа проблемы ( F = m g – см. анекдот в эпиграфе, T = m c 2 и т.д.), но и полученные после статистической обработки экспериментальных данных. Коэффициенты таких формул (см., например, рис. 12 ниже), как правило, жестко связаны с той или иной системой единиц измерения и нередко требуют пересчета для использования в программе. Это может вносить дополнительные погрешности и чревато ошибками (промахами).
Пакет Mathcad полностью поддерживает математику работы с размерными переменными, что и будет описано данной статье.
записывая размерность введенной величины в виде комментария, а не в виде множителя у числовой константы и отключая тем самым размерности физических величин из дальнейших расчетов.
Механизм работы с единицами измерений физических величин позволяет в среде Mathcad:
· вводить исходные данные в нужной системе измерений и в нужных единицах измерений;
· вести контроль размерностей в формулах, по которым проводятся расчеты (не складывать килограммы с метрами, грубо говоря);
· выводить рассчитанные данные в нужной системе измерений и в нужных единицах измерений;
Механизм работы с размерными величинами будет проиллюстрирован примерами.
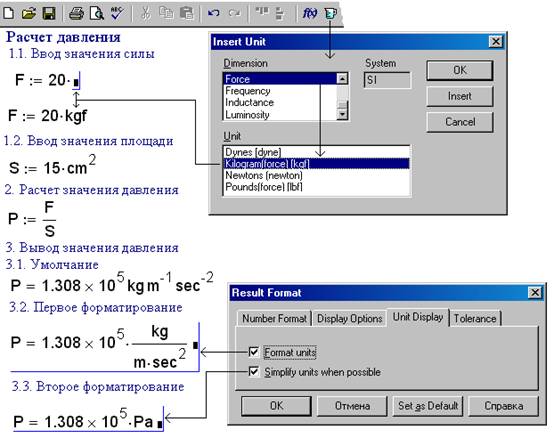
Рис. 1. Расчет давления в среде Mathcad
Физические задачи в среде Mathcad не просто могут, но и должны решаться с подключением единиц измерения физических величин – силы, площади и давления, если иметь в виду нашу задачу. В Mathcad документе по умолчанию синим цветом окрашены комментарии, а черным – математические выражения, а именно:
· Пункт 2. Расчет значения давления. Переменная P при этом принимает не только числовое значение (результат деления значения переменной F на значение переменной S ), но и результат деления килограмма силы на квадратный сантиметр, вернее просто силы на площадь.
· Пункт 3. Вывод рассчитанного значения давления:
· Пункт 3.2. Вывод единиц измерения не в виде одной строки, а в виде дроби: первый шаг форматирования – см. галочку в поле Format Units окна Result Format на рис. 1. Данное окно вызывается на дисплей двойным щелчком по числовому результату.
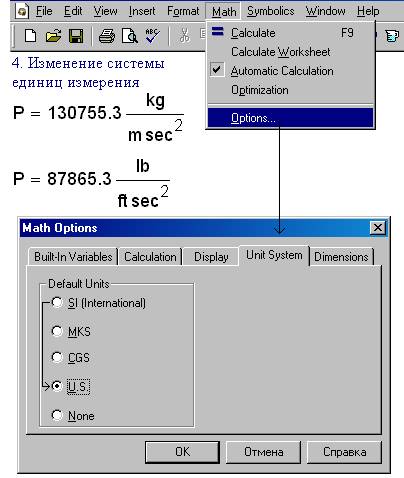
Рис. 2. Изменение системы измерений
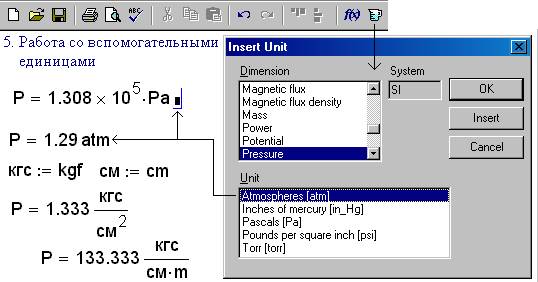
Рис. 3. Смена единиц измерения давления
Рис. 4. Работа с пользовательской нефизической (экономической) величиной
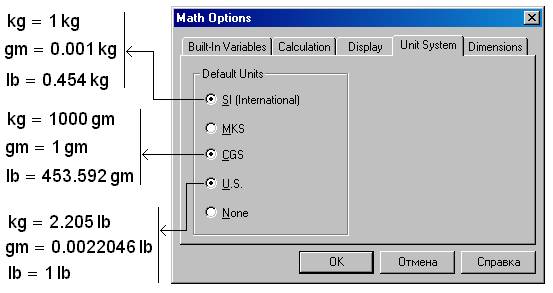
Единицы измерения физических величин – это по своей сути предопределенные переменные, хранящие размерные величины, «вид» которых зависит от выбранной системы измерений – см. рис. 5, где показаны «метаморфозы» трех основных единиц измерения массы: килограмма ( kg ), грамма ( gm ) и английского фунта ( lb [11] ).
Рис. 5. Что хранят единицы измерения массы
На рис. 5 показано, как будут выглядеть три оператора вывода основных единиц массы, если менять систему измерений.
Рис. 6. Контроль размерности переменной
Для контроля размерности переменной можно использовать и встроенную функцию UnitsOf (см. рис. 6), возвращающую единицу измерения своего аргумента.
Рис. 7. «Размерный» график
Элементы Mathcad документа (ввод исходных данных, расчет по формулам, вывод результатов) выполняется в их естественной последовательности – сверху вниз и слева на право. Пользователь Mathcad может нарушить этот порядок, организовав циклы (часть операторов выполняется циклически до тех пор, пока не будет выполнено некое условие) или альтернативы (выполняется либо одна, либо другая группа операторов). Еще два атрибута программирования в среде Mathcad – это объединение части (группы) операторов в операторный блок, который выполняется как один оператор, и работа с локальными переменными, видимыми только внутри программного блока.
Последующие два рисунка (рис. 8 и рис. 9) проиллюстрируют особенности использования единиц измерения в Mathcad-программах.
Рис. 8. Размерность в программах
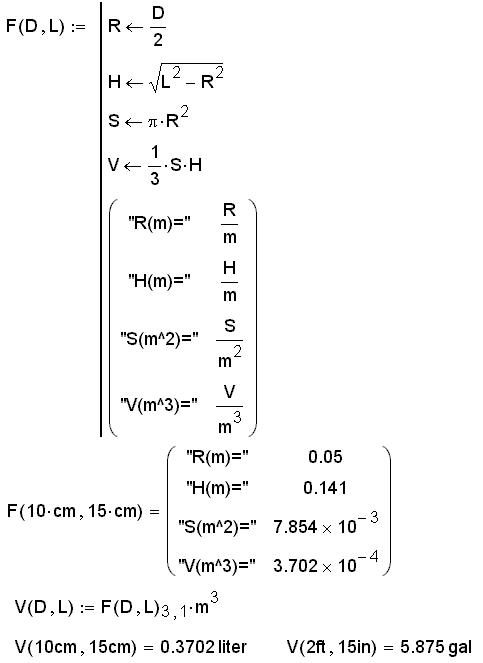
Британский или английский пользователь Mathcad может тут использовать футы и/или дюймы, но на работу функции V это не повлияет: вызывая ее, можно использовать любые единицы длины и объема – см. примеры на рис. 8.
Рис. 9. Функция, возвращающая «букет» переменных
Из формируемой матрицы можно изъять нужный элемент, припечатав к нему нужную единицу измерения:
Рис. 10. Работа с «житейскими» градусами в среде Mathcad
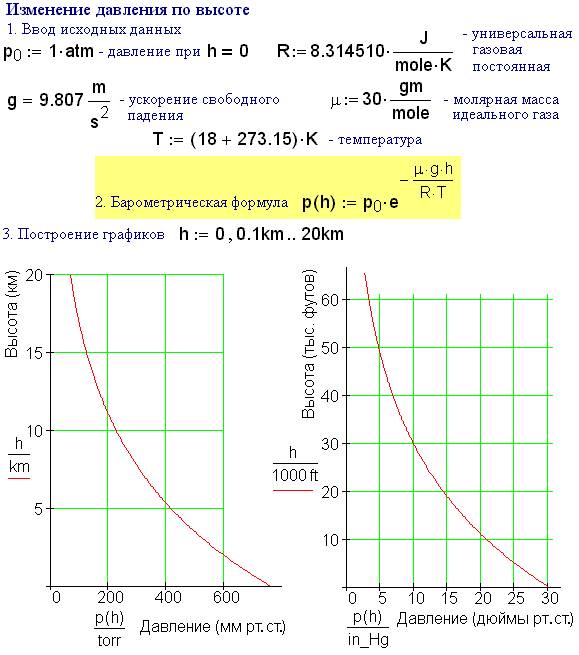
Героям рассказа Марк Твена достаточно было перенести показания барометра на ординату графика на рис. 7, чтобы узнать высоту над уровнем моря. Кипятить термометр следовало лишь в том случае, если бы под рукой не оказалось барометра.
Рис. 11. Определение высоты по температуре кипятка
Серьезный разбор задачи о высоте над уровнем моря – это дело не совсем «серьезное». И не только потому, что юмор Марк Твена всячески «сопротивляется» этому. Дело и в том, что барометрическая формула предназначена только для идеального газа. Кроме того, давление воздуха на одной и той же высоте может сильно колебаться. Температуру воздуха мы приняли за 5 градусов Цельсия, а она сильно изменяется по высоте.
Но цель нашего расчета не в разборе рассказа, а в показе возможностей Mathcad при решении «размерных» задач (тема статьи, если кто-то забыл).
Использование размерностей физических величин в среде Mathcad позволяет по-новому организовать расчеты по эмпирическим формулам, переменные которых «намертво» привязаны к определенным единицам измерения. Переход к новым единицам требует перезаписи формул.
При записи этой же формулы с использованием системы единиц СИ значение постоянного множителя в правой части формулы (1) изменяется.
Необходимо определить новое значение этого множителя. Обозначим его буквой С, тогда:
Подставляя коэффициенты из одной системы единиц в формулу для расчета теплоотдачи при кипении, получаем новое значение постоянного множителя:
и в новых единицах формула (1) примет вид:
На рис. 12 показано решение этой «метрической» проблемы в среде Mathcad.
Рис. 12. Работа с эмпирическими формулами в среде Mathcad
Если формула оперирует только определенными единицами измерений и возвращает ответ с оговоренной единицей, то эти оговорки необходимо записать в формуле так, чтобы при обращении к ней можно было пользоваться любыми встроенными или пользовательскими единицами измерений (см. подсвеченные операторы на рис. 12).
При работе с размерностями Mathcad может возникать интересная ситуация, связанная с округлением степени единицы измерения физической величины до целых значений. На рисунке ниже показана такая ситуация, когда по ошибке или специально из литра извлекается квадратный корень:
Mathcad выдает ответ: квадратный корень из литра равен стольким-то метрам в первой степени, т.е. просто метрам, что смущает вдумчивых пользователей, которые вполне законно делают вывод о том, что Mathcad не совсем корректно работает с размерностями. Но здесь дело в том, что Mathcad округляет до целого степень единицы измерения. Если подставить в ответ другую единицу измерения (метр в степени полтора), то все станет на свои места (см. выше).
Один персонаж Аркадия Райкина (алкоголик) измерял комнату чекушками (бутылками в 0,25 литра водки), а потом пытался высчитать площадь в «квадратных литрах». Он был не очень далек от истины:
Литра будет служить в качестве единицы площади, если его возвести в соответствующую дробную степень (две трети).
Дивертисмент
В романе Агаты Кристи «Убийство в Месопотамии» читаем: «Начнем с того, что его рост, на мой взгляд, не превышал пяти футов и пяти дюймов». Загадка роста знаменитого сыщика – Эркюля Пуаро разгадывается в среде Mathcad одним оператором:
5 ft + 5 in = 165.1 cm
Более сложную загадку о росте своего героя оставил нам И.С. Тургенев. Второй абзац знаменитой повести «Муму» начинается так: «Из числа всей ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырем и глухонемой от рождения».
вершок := 4.445 см (В справочник мы все-таки заглянули)
12 вершок [26] = 53.36 см
Герасим, судя по этому подсчету, не дотягивал не то что до богатыря – не тянул на карлика. В чем тут дело!?
Гипотеза первая. Тургенев, описывая Герасима, имел в виду не простые, а какие-то особые вершки. Ведь есть сажень, а есть косая сажень («косая сажень в плечах!»), маховая сажень, есть метрическая тонна, а есть «длинная» тонна, «короткая» тонна, есть сухопутная миля, а есть морская и т.д. Но поиск [27] таинственных «удлиненных» вершков окончился неудачей – вершки оставались вершками: семь четвертых дюйма, одна четвертая пяди, одна шестнадцатая аршина, одна сорок восьмая сажени и т.д.
Более вероятной представляется другая гипотеза, связанная с принципом умолчания. Дело в том, что рост человека, как правило, укладывается в диапазоне от 2 до 3 аршин:
Аршин := 16 вершок (вершки определены выше)
Три аршина – это хороший баскетболист, а два аршина – рулевой восьмерки в академической гребле.
Опираясь на изложенную гипотезу, несложно подсчитать рост Герасима:
2 аршин + 12 вершок = 195.58 см
Вот это нормальный богатырский рост! (Развитие и некоторое дублирование темы – см. статью Mathcad и некоторые тайны художественной литературы, журнал Домашний компьютер, № 5, 2000).