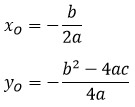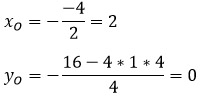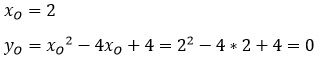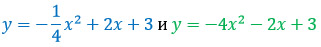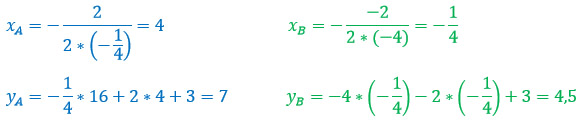Как сделать график квадратичной функции
Квадратичная функция. Построение Параболы
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
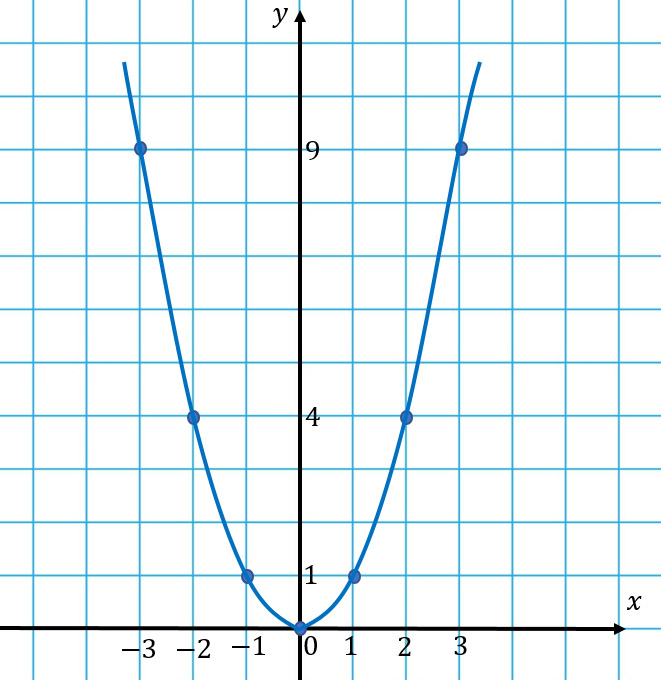
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
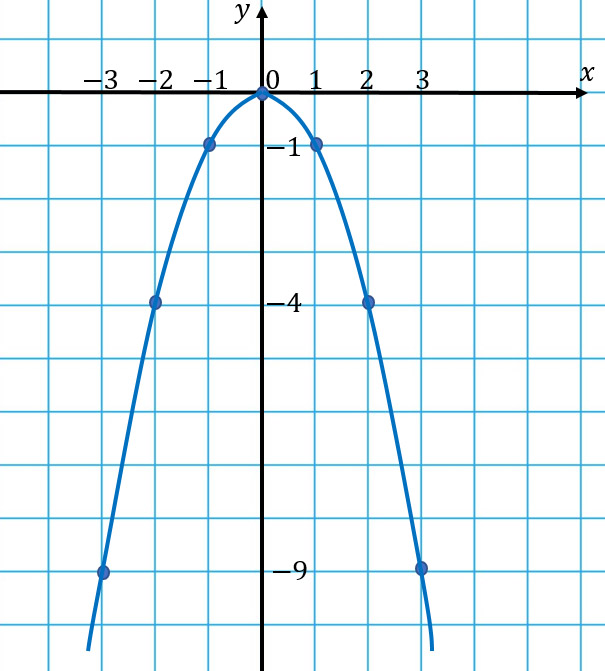
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)
Как строим:
Чтобы не запутаться во всех графиках, приходите вместе с ребенком на бесплатный урок математики в современную школу Skysmart: порисуем параболы на интерактивной онлайн-доске, разберемся в самых коварных формулах и покажем, что математика может быть увлекательным путешествием.
Квадратичная функция (ЕГЭ – 2021)
Построение графика квадратичной функции, ее области определения, коэффициенты, вершина параболы, все варианты ее расположения.
Все, что нужно знать для сдачи ОГЭ и ЕГЭ, в одном месте.
ШПОРА ПО КВАДРАТИЧНОЙ ФУНКЦИИ
Квадратичная функция – функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (коэффициенты), \( c\) – свободный член.
График квадратичной функции – парабола.
Вершина параболы: \( \displaystyle <
Квадратичная функция вида: \( y=a<
Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире.
Варианты расположения параболы в зависимости от коэффициента \( \displaystyle a\) и дискриминанта \( \displaystyle D=<^<2>>-4ac\).
Для построения параболы необходимо:
Для начала скажи мне, что такое функция?
Не знаешь? Тогда сперва прочитай тему «Функции» – она несложная, но очень важная.
А мы пока повторим.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»? Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!
Все дело в понятии «область определения»:
Для некоторых функций не все аргументы можно подставить в зависимость.
Например, для функции \( y=\sqrt
Кстати, а с линейной функцией ты уже дружишь? Про нее все написано в теме «Линейная функция» – там ты поймешь, что в функциях ничего страшного нет и научишься понимать и использовать коэффициенты (это циферки перед буквой \( x\)).
И еще, надеюсь, ты умеешь решать квадратные уравнения? Освежить память можно, почитав тему «Квадратные уравнения».
Понятие квадратичной функции
Квадратичная функция – это функция вида \( y=a<
^<2>>+bx+c\), где \( a\ne 0\), \( b\) и \( c\) – любые числа (они и называются коэффициентами).
Число \( a\) называют старшим или первым коэффициентом такой функции, \( b\) – вторым коэффициентом, а \( c\) – свободным членом.
Другими словами, квадратичная функция – это зависимость, содержащая аргумент в квадрате. Отсюда и ее название.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений\( E\left( y \right)\).
Какими могут быть значения аргумента квадратичной функции \( y=a<
Значит, область определения – все действительные числа:
А теперь множество значений. Все ли значения может принимать функция?
Достаточно рассмотреть самую простую квадратичную функцию \( y=<
\), чтобы убедиться в обратном: ведь какое бы число мы не возводили в квадрат, результат всегда будет больше или равен нулю. Значит, эта функция всегда не меньше нуля. А вот больше нуля она может быть сколько угодно: ведь бесконечно большой x в квадрате будет еще больше. Таким образом, можем написать для \( y=<
В каждом отдельном случае область значений будет разная, но всегда – ограниченная.
Квадратичная функция. График
Наверняка ты слышал, что график квадратичной функции называется параболой. Как она выглядит? Сейчас нарисуем.
Построение графика квадратичной функции
Начнем с простейшей квадратичной функции – \( y=<
Составим таблицу значений:
Нарисуем эти точки на координатной плоскости и соединим их плавной линией:
Именно так и выглядит парабола. Самая нижняя ее точка называется вершиной, а части спарва и слева от вершины называем ветвями параболы. Как видим, ветви симметричны относительно вертикали, проходящей через вершину.
Рассмотрим теперь другую функцию: \( y=<
Составим таблицу значений:
Сравним два рисунка. Видно, что это как будто одна и та же парабола, просто расположенная в разных местах. Во второй параболе вершина переместилась в точку \( \left( 1;-4 \right)\), а ветви переехали вместе с ней. Да, так оно и есть: все параболы с одинаковым старшим коэффициентом, a выглядят одинаково – даже при разных остальных коэффициентах.
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
Регистрируйся здесь и приходи!
Коэффициенты квадратичной функции
Давай разберем, на что влияют коэффициенты квадратичной функции.
Начнем со старшего коэффициента.
Будем рассматривать функции вида \( y=a<
Что ты видишь? Чем они отличаются? Какую закономерность можно заметить?
Во-первых, это невозможно не заметить, если \( \displaystyle \mathbf \mathbf<0>\) – вверх.
Так, хорошо. Значит, если парабола пересекает ось \( \displaystyle Ox\) в двух точках, то у нас два корня квадратного уравнения. Если не пересекает – корней нет. Но бывает ведь, что дискриминант уравнения равен нулю, и тогда только один корень. В этом случае парабола касается оси \( \displaystyle Ox\) вершиной:
А что такое вершина параболы?
Вершина параболы
Корень уравнения в этом случае указывает на вершину параболы. Если вспомнить формулу корня квадратного уравнения при \( \displaystyle D=0\), получим формулу вершины:
Это тоже бывает очень полезно.
Итак, всего возможны шесть разных вариантов расположения параболы. Вот они все на одном рисунке:
Пройди эти 4 урока и ты научишься решать экономическую задачу любой сложности с самого нуля, шаг за шагом. Подробно о том, что входит в курс можно прочитать здесь.
А теперь порешаем задачки.
Примеры решения задач
1. График какой из функций избражен на рисунке?
2. Найдите сумму корней квадратного уравнения \( a<
3. Найдите произведение корней квадратного уравнения \( a<
4. По графику функции \( y=<
Решения:
1. Первое: куда «смотрят» ветви параболы? Вниз. А что это значит? Правильно, \( \displaystyle a d)
2. Проще простого: корни – это точки пересечения параболы с осью \( \displaystyle Ox\).
Смотрим: \( \displaystyle <
3. То же самое: \( \displaystyle <
4 . Хм… Ну, коэффициент с мы бы нашли, да только по оси \( \displaystyle Oy\) нет обозначений. Зато показаны точки пересечения с осью \( \displaystyle Ox\). А это ведь корни уравнения \( \displaystyle <
Как это нам поможет?
Кстати, чему равен старший коэффициент?
Он равен \( \displaystyle 1\). Как называется такое квадратное уравнение? Вспоминай: оно называется приведенным. Теперь догадался? Можно ведь применить теорему Виета. Точно! Ведь она говорит нам, что сумма корней равна второму коэффициенту с обратным знаком:
а произведение – свободному члену:
P.S. Последний бесценный совет!
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут. Почему? Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем большинство твоих сверстников. Проблема в том, что этого может не хватить…
Для успешной сдачи ЕГЭ и поступления в ВУЗ мечты на бюджет и, самое главное, для жизни. Я не буду тебя ни в чем убеждать, просто скажу одну вещь… Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил.
Это статистика. Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Что нужно, чтобы сдать наверняка ЕГЭ, поступить в ВУЗ мечты и быть в конечном итоге… более счастливым? Две вещи.
Первое, тебе нужно набить руку, решая задачи
На экзамене у тебя не будут спрашивать теорию. Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка. “Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
И сейчас будет честная реклама наших курсов подготовки к ЕГЭ, потому что они решают обе эти проблемы.
Тебе же понятен этот учебник? Так вот наши курсы такие же понятные как этот учебник.
Потому что их подготовил и ведет автор этого учебника Алексей Шевчук.
Он буквально разжевывает все на вебинарах. Вы решаете задачи. Много задач. У вас будет проверка домашки и марафон «Год за месяц» в мае, чтобы «упаковать» ваши знания и улучшить результат на 20-30%.
Курсы очень бюджетные: от 2000 до 3990 тыс/мес за 12 двухчасовых занятий с Алексеем.
Кликайте по этим кнопкам и читайте условия, там все очень подробно описано:
Квадратичная функция и её график
Парабола является графиком квадратичной функции, которая задается формулой y = ax 2 + bx + c.
Нарисовать параболу можно, используя таблицу значений, в которой мы выбираем произвольный х и находим у. Но не всегда этот способ является самым рациональным.
Начнем, как всегда, с простого)
Стандартная парабола.
На координатной плоскости отмечаем эти точки и чертим параболу.
Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:
Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя «на ура».
Параболы со смещенной вершиной.
Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции y = ±x 2 + bx + c (обязательно коэффициент перед х 2 должен равняться ±1) является стандартной параболой, только вот вершины этих парабол не будут находится в начале координат.
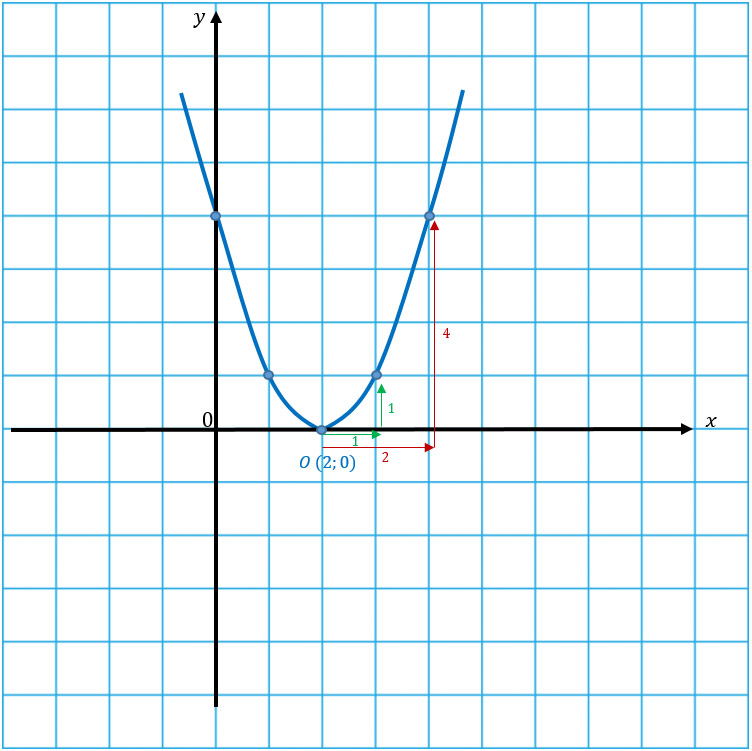
Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.
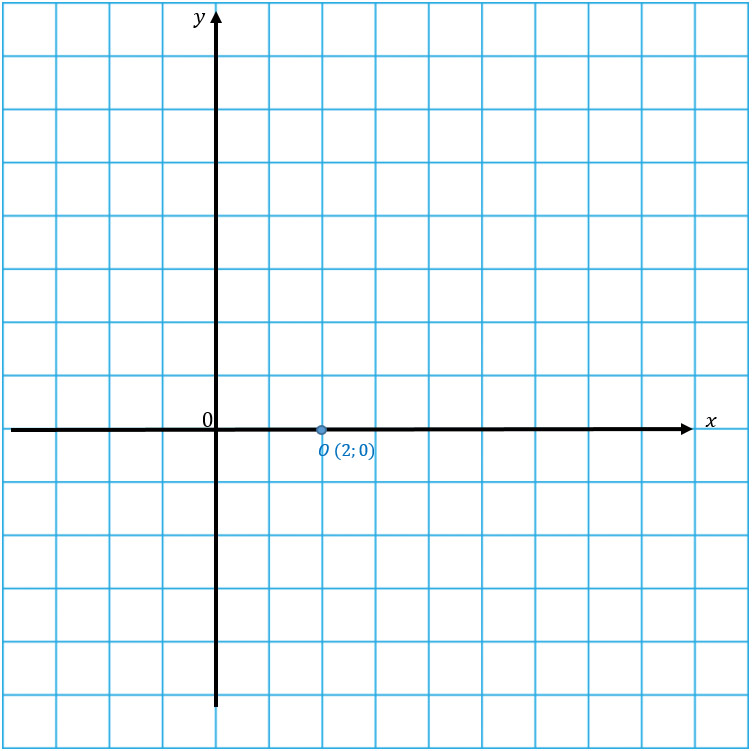
Пусть вершиной параболы будет точка О с координатами (x1; y1). Тогда найти эти координаты можно по формулам:
Кстати, можно найти координаты вершины и другим способом.
Координату хО находим по той же формуле, а координату уО можно найти подстановкой координаты хО в функцию.
Без примера не обойтись)
Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.
1 способ: по формулам.
2 способ: подстановкой.
Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.
Параболы-стройняшки и параболы-пухляшки.
Удивительно, но числовой коэффициент перед х 2 оказывается влияет на стройность и полноту парабол.
Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.
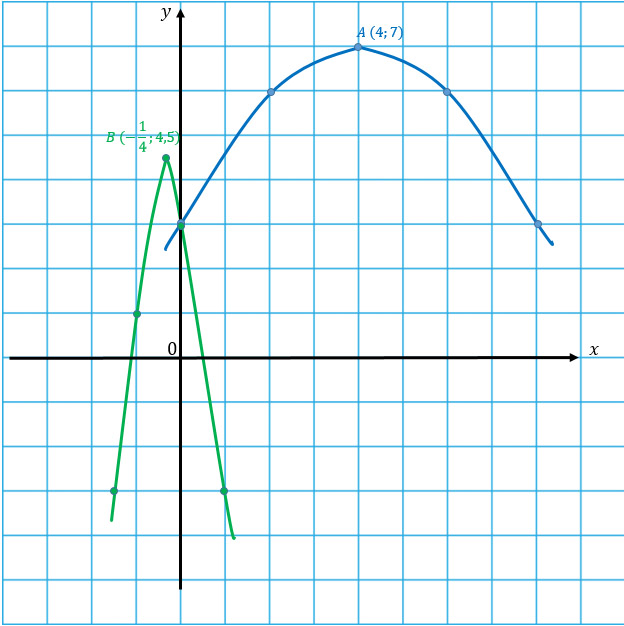
Не веришь? Давай проверим! Для примера возьмем две функции:
К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.
Переходим к таблицам значений.
| x | 0 | 2 | 4 | 6 | 8 |
| y | 3 | 6 | 7 | 6 | 3 |
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
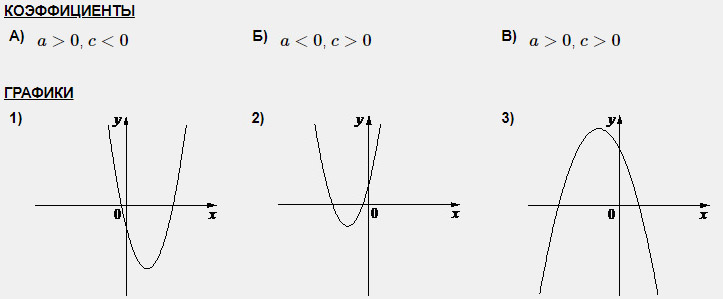
Задание 1. На рисунке изображены графики функций вида y = ax 2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 2.
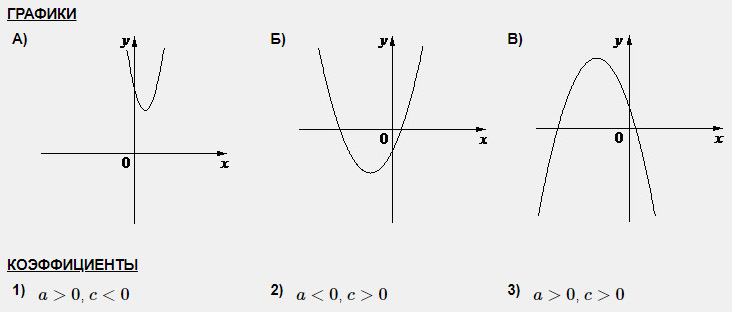
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax 2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с 0. Подходит вариант под номером 2.
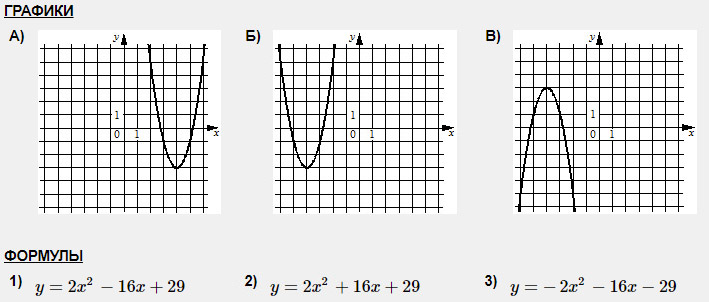
Задание 3. Установите соответствие между графиками и их функциями.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
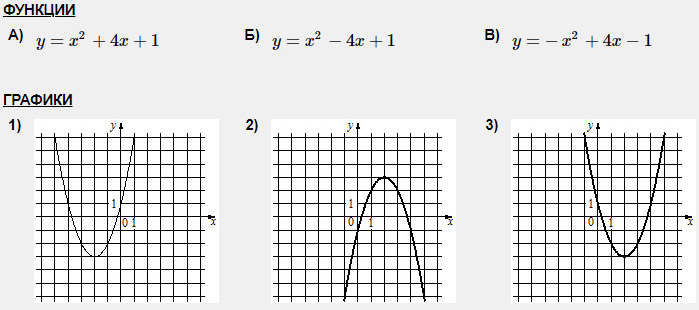
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!