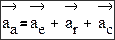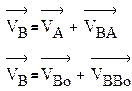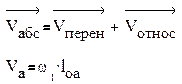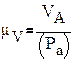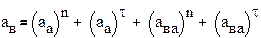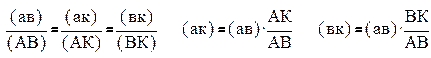Как сделать график перемещения

Как сделать график перемещения

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

V_x — Скорость тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

a_x — Ускорение тела

t — Время движения тела

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [м/с 2 ].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения: v_x = v_xo + a_xt

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

S_x — Перемещение тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

V_x — Скорость тела при равноускоренном движении по прямой

a_x — Ускорение тела

t — Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

— если известны начальная, конечная скорости движения и ускорение.

— если известны начальная, конечная скорости движения и время всего движения

Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:

В координатах зависимость имеет вид:

Источник

Построение диаграммы перемещения.

Строим 12 положений (см.рис.1)

За начало отсчета принимаем положение поршня В_о.

k-коэффициент кратности ординат графика S_в=S_в(t) и

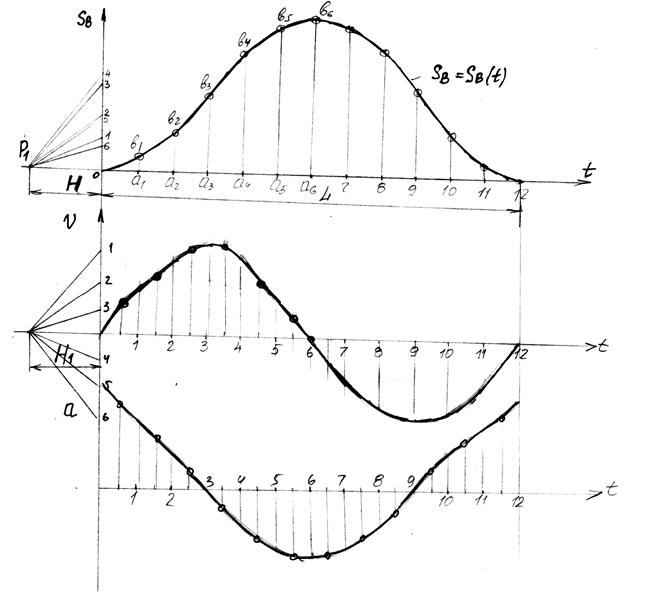
отрезков изображающих перемещения B_oB₁, B_oB₂ т.В на планах механизма.

Между масштабом плана механизма и масштабом ординат диаграммы пе­ремещений существует зависимость:

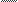μs=

1k

*μe

Масштаб времени, откладываемого по оси абсцисс:

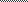μt=

T L

(сек./мин.)

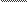T=

n

(сек) при этом

μt=

nT

(сек./мин.)

Аналогично строится график угловых перемещений звена совершающее вращательное движение. В этом случае по оси ординат откладываются от­резки пропорциональные величинам угловых перемещений.

Построение графиков скорости и ускорения по графику перемещения.

Построение графиков V=V(t) и a=a(t) по графику S=S(t) осуществля­ется методом графического дифференцирования, сущность которого заключа­ется в следующем.

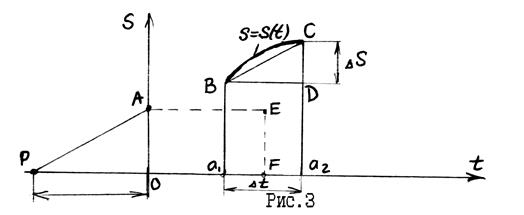
Пусть есть перемещение некоторой точки за малый промежуток времени. Проведем секущую ВС, а из полюса Р, выбранного произвольно на расстоя­нии Н от начала координат луч, параллельный ВС. Из подобия РАО и ВОД следует:

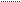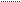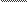OA H

=

CD BD

OA=

CD BD

*H

(1)

Действительное значение перемещения за время отображается отрезком:

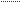CD=

∆S μs

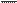отрезок оси абсцисс

а1 а2 =

BD=

∆t μt

-отображает длительность интервала времени в масштабе.

Подставив эти значения CD и BD в равенство (1) найдем:

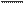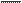OA=

∆S ∆t

*

μt μs

*H

(2)

отношение представляет среднее значение скорости движения точки на пу­ти длинной ∆S, то следует:

Vср=

ОА*

μs μt* H

(3)

Если принять масштаб скорости

μV=

μs μt* H

то из равенства (3) отрезок ОА

отображает величину средней скорости движения точки.

Допуская некоторую погрешность, считают, что это среднее значение скорости соответствует среднему мгновению промежутка t, т.е. точке F.

При изложенном способе дуга ВС заменилась хордой ВС. Допустима также замена дуги соответствующим отрезком касательной. В обоих случаях результаты получаются с погрешностью.

(Рассмотрим на примере рис.2)

График ускорения строится аналогично, путем дифференцирования гра­фика V. При этом новое полюсное расстояние H₁≠H

Определение масштаба графика a получаем, заменив величину μ_s→μ_V а вместо H→H₁

μa=

μV μt*H1

Вследствии двукратного дифференцирования, диаграммы a могут по­лучиться со значительными искажениями.

Поэтому рассмотрим другой способ определения скоростей и ускорений.

Метод планов скоростей и ускорении базируется на теоремах о скольжении векторов скоростей и ускорений, доказываемых в курсах теоре­тической механики.

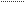Теорема 1 Вектор скорости абсолютного движения точки (V_a) равен сумме

векторов скоростей переносного (V_e) и относительного (V_r) движений.

эта теорема была известна еще Архимеду (287-212 гг.д.н.э.)

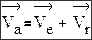
Теорема 2 (Кориолиса) Вектор ускорения (а_n) абсолютного движения материальной точки равен сумме векторов ускорений переносного (а_е) и

относительного движений (а_r) и ускорения Кориолиса (a_c):

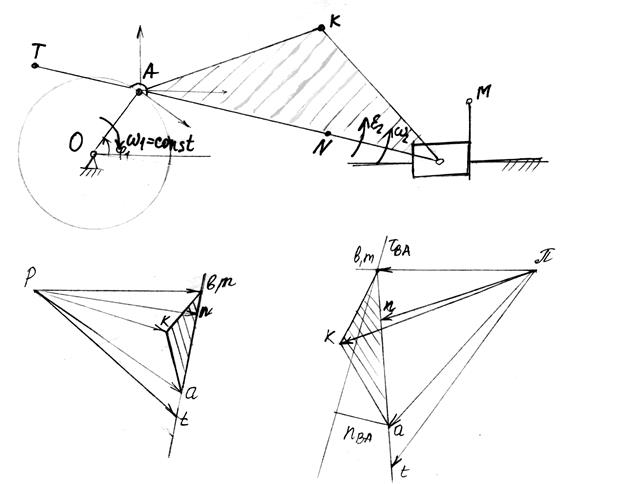
Метод планов скоростей и ускорений.

V_ВА^ВА

Все точки координатной системы движутся с одинаковой скоростью. Пос­ле того, как найдены скорости шарнирных точек механизма, скорости дру­гих точек определяем с помощью теоремы подобия:

все жесткие фигуры на плане механизма подобны одноименным фигурам на плане скоростей, а их сходственные стороны взаимно перпендику­лярны.

Планы ускооений

-теорема о сложении ускоре­ний, когда переносное ускорение по форме поступательное.

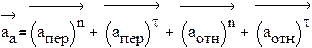
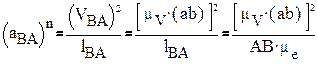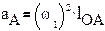Для определения ускорения остальных точек используем теорему по­добия: все неизменяемые фигуры на плане механизма подобны одноименным фигурам на плане усковений.

Методом засечек получим две точки, одна из них ложная, чтобы найти истинную точку, применяют правило обхода вершин:

порядок чтения вершин при обходе подобных контуров в какую-ли­бо, но одну и ту же сторону, не должен изменяться.

Определение угловых скоростей и угловых ускорений звеньев механизмов

Шатун АВ вращается ускоренно, т.к. ω₂ и ε₂ направлены в одну сторону. Если ω и ε направлены в разные стороны, то ползун движется замедленно.

Механизмы с высшей кинематической парой.

В этом разделе будут рассмотрены передаточные механизмы с высшей КП, а именно:

1. цилиндрические зубчатые передачи с эвольвентным профилем зубов и постоянным передаточным отношением;

2. планетарные механизмы с подвижными осями зубчатых колес.

Достоинство механизмов с высшей КП:

1. малые габариты и вес;

2. возможность точного воспроизведения закона движения выходного звена (по сравнению с рычажными механизмами зубчатые передачи имеют меньше зазоров);

3. высокий КПД (0,85 – зубчатая передача, 0,99 – планетарный механизм).

Недостатки:

наличие высшей КП может привести к повышенным удельным давлениям в точке контакта. Это в свою очередь может привести к выкрашиванию материалов (питтинг).

Дата добавления: 2019-07-26 ; просмотров: 309 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Как по графику скорости посчитать перемещение

По графику скорости от времени v(t) можно найти перемещение тела. Для этого нужно уметь рассчитывать площади плоских фигур.

По-английски «Square» – значит «площадь». Первая буква этого слова – буква «S». Перемещение обозначают буквой S потому, что S – это площадь фигуры, заключенной между линией скорости и горизонтальной осью времени.

Как вычислить площади плоских фигур

Площадь прямоугольника

Площадь прямоугольника (рис. 1а) можно найти, перемножив две его перпендикулярные стороны:

Площадь трапеции

Примечание: Трапеция – это четырехугольник, две его стороны параллельные, а две другие – не параллельные. Параллельные стороны называются основаниями трапеции.

Умножив полусумму оснований трапеции на ее высоту, получим площадь (рис. 1б) трапеции:

Площадь прямоугольного треугольника

Для прямоугольного треугольника (рис. 1в) площадь можно вычислить, перемножив два его катета и взяв половину от получившегося произведения:

Скорость не меняется

Пусть тело движется по прямой и при этом его скорость не изменяется (остается одной и той же). На языке математики «скорость не изменяется» можно записать так:

На графике для скорости v(t) такая скорость обозначается горизонтальной линией. На рисунке 2 эта линия обозначена синим цветом.

Примечание: Движение с постоянной (т. е. с одной и той же) скоростью называют равномерным движением.

Если скорость направлена по оси движения – линия лежит выше оси t времени (рис. 2а).

А когда скорость направлена против оси движения – линия скорости располагается ниже оси t времени (рис. 2б). Математики в таком случае говорят: «Скорость имеет отрицательную проекцию на ось».

Какую бы проекцию не имела скорость – положительную, или отрицательную, длина вектора скорости остается положительной. Поэтому, когда мы вычисляем площадь фигуры, то не учитываем знак «минус» для скорости (рис. 2б).

В обоих случаях перемещение тела можно вычислить по формуле:

\[ \large S = v_ <0>\cdot (t_ <2>— t_<1>) \]

Примечание: Перемещение тела – это всегда либо нулевая, либо положительная величина S. Математики словосочетание «либо нулевая, либо положительная» заменят одним словом «не отрицательная».

Скорость увеличивается

Когда скорость тела увеличивается, то линия скорости на графике v(t) всегда располагается так, чтобы с ростом времени удаляться от оси времени. Чем больше времени пройдет, тем дальше от горизонтали располагаются точки, лежащие на линии скорости (рис. 3).

Примечание: Движение с возрастающей скоростью называют равноускоренным движением.

Когда тело движется по направлению оси, линия скорости расположена выше горизонтальной оси времени (рис 3а).

А если тело движется против оси, линия скорости располагается ниже горизонтальной оси времени (рис. 3б).

Вычислим перемещение тела, движущегося в положительном направлении оси Ox. Для тела, движущегося противоположно оси, перемещение рассчитывается аналогично.

Выбор интервала времени влияет на то, будем ли мы вычислять площадь трапеции (рис. 4а), или прямоугольного треугольника (рис. 4б).

На графике скорости v(t) для рисунка 4а перемещение с помощью трапеции вычисляется так:

\[ \large S = \frac<1> <2>\cdot (v_ <1>+ v_<2>) \cdot (t_ <2>— t_<1>) \]

А для рисунка 4б перемещение тела найдем с помощью площади треугольника:

\[ \large S = \frac<1> <2>\cdot v_ <2>\cdot (t_ <2>— 0) \]

Скорость уменьшается

Когда тело замедляется и его скорость уменьшается, с ростом времени линия скорости приближается к горизонтальной оси t

Примечание: Движение с уменьшающейся по модулю скоростью называют равнозамедленным движением.

Будем вычислять перемещение тела, движущегося в положительном направлении оси Ox. Аналогичным способом рассчитывается перемещение тела, движущегося противоположно оси.

От того, какой интервал времени нас интересует, зависит, будем ли мы вычислять площадь трапеции (рис. 6а), или треугольника (рис. 6б).

Найдем на графике v(t) перемещение с помощью площади трапеции для рисунка 6а:

\[ \large S = \frac<1> <2>\cdot (v_ <1>+ v_<2>) \cdot (t_ <2>— t_<1>) \]

А для рисунка 6б перемещение тела найдем с помощью площади треугольника:

\[ \large S = \frac<1> <2>\cdot v_ <1>\cdot (t_ <2>— t_<1>) \]

Выводы

На графике v(t) перемещение – это:

Источник