Как сделать график статистики
Построение графиков в Excel по данным таблицы
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
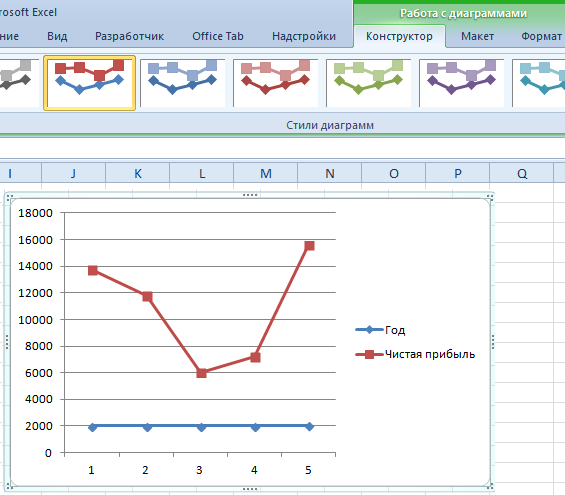
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
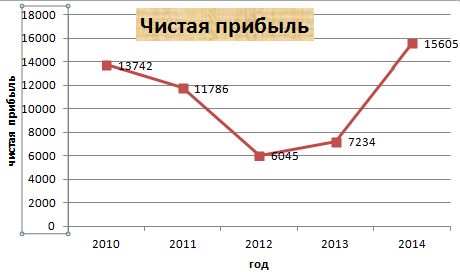
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
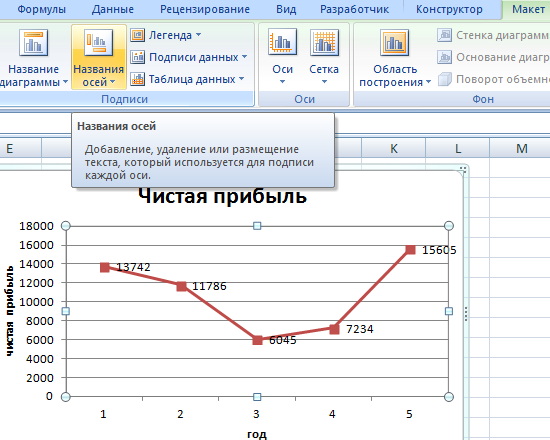
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
График с двумя и более кривыми
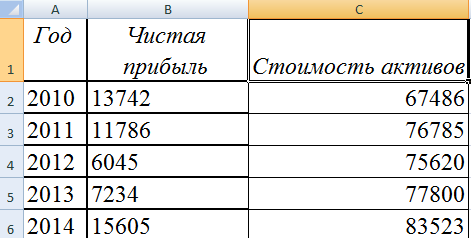
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
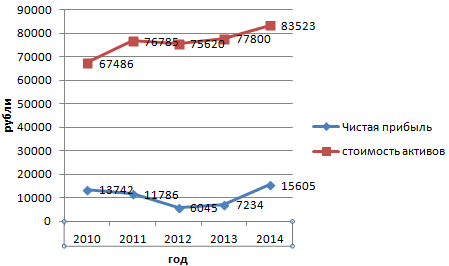
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
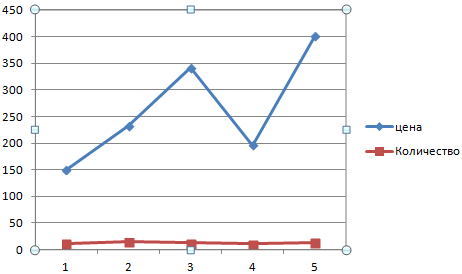
Сначала строим график так, будто у нас одинаковые единицы измерения.
Это один из способов. Есть и другой – изменение типа диаграммы.
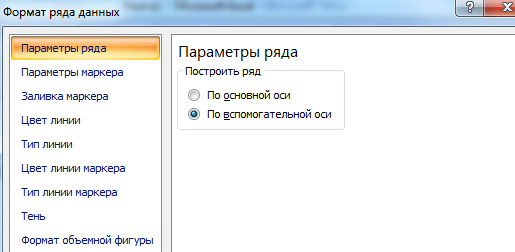
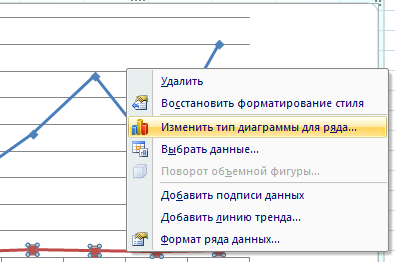
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
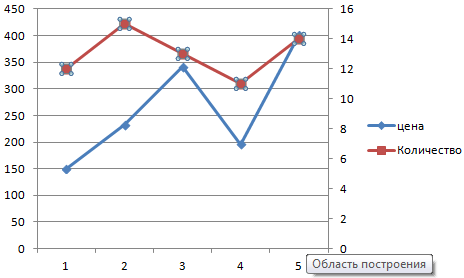
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
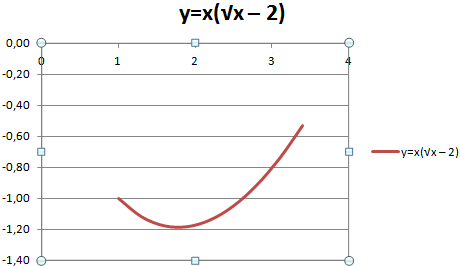
Пример: y=x(√x – 2). Шаг – 0,3.
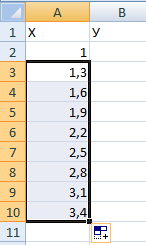
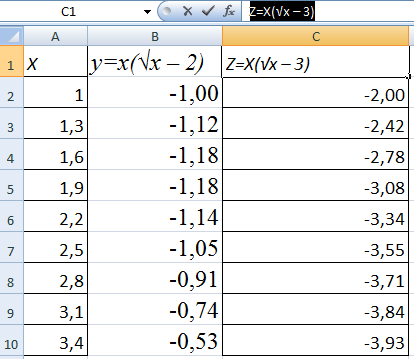
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
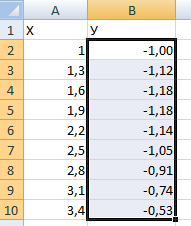
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
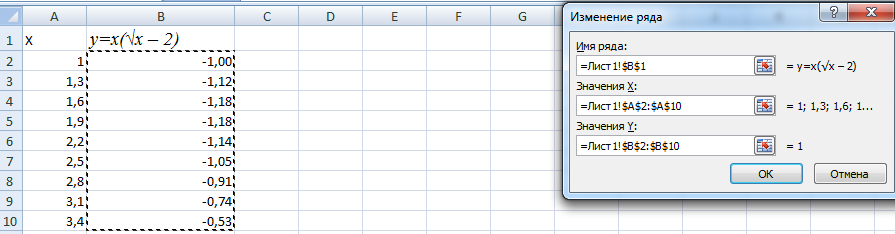
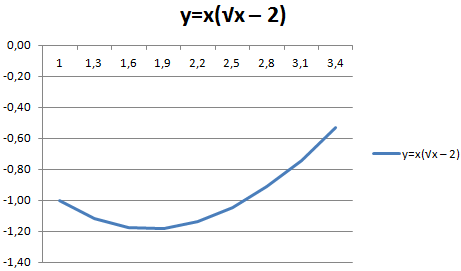
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
Наложение и комбинирование графиков
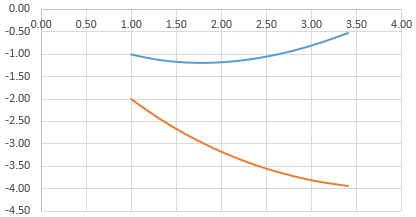
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
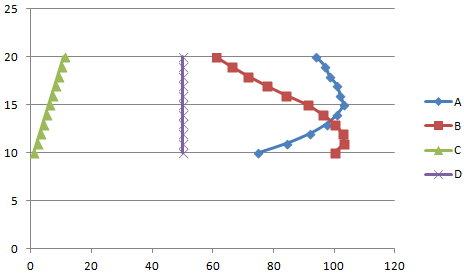
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Готовые примеры графиков и диаграмм в Excel скачать:
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Особенности построения статистических графиков
Графиками в статистике называют чертежи, в которых наглядные изображения статистических величин даются с помощью условных геометрических образов — точек, линий, фигур и т.п.
В статистическом графике различают следующие основные элементы построения: поле графика, графический образ, пространственные и масштабные ориентиры, экспликация графика.
Поле графика — это плоскость, на котором он выполняется (лист бумаги, магнитная лента, географическая карта, план местности и т.п.). Поле графика характеризуется его форматом, т.е. размером и пропорциями (соотношениями сторон).
Графический образ — это совокупность точек, линий, фигур, с помощью которых на поле графика изображаются статистические данные.
Пространственные ориентиры определяют размещение графических образов на поле графика. Они задаются координатной сеткой или контурными линиями и делят поле графика на части, соответствующие значением изображаемых показателей. Пространственные ориентиры позволяют определить расположение графических образов на поле графика. Для этого чаше всего применяется прямоугольная (декартова) система координат, хотя возможны построения по принципу полярных координат (круговые графики).
Масштабные ориентиры задаются масштабом и системой масштабных шкал.
Масштаб графика — это условная мера перевода числовой величины в графическую (например, 1 см некоторого знака соответствует 100 руб. продукции).
Масштабная шкала — это линия, отдельные точки которой согласно принятому масштабу соответствуют определенным значениям статистического показателя. Масштабные шкалы могут быть прямолинейными и криволинейными, равномерными и неравномерными. Чаще применяются прямолинейные равномерные масштабные шкалы, которые располагаются по осям координат и делятся на графические отрезки, пропорциональные числам, наносимым на шкалу. При построении таких графиков важно соблюдать масштаб: если, например, какое-то число удвоится, то и отрезок шкалы должен быть вдвое больше. Отсчет уровней на шкале обычно начинается с нуля. При построении графика допускается разрыв масштабной шкалы.
Экспликация графика — это словесное пояснение его содержания: включает в себя название графика, надписи вдоль масштабных шкал, пояснения к отдельным частям графика (легенда).
По способу построения графики подразделяются на диаграммы и статистические карты (рис. 3.2).
Рис. 3.2. Статистические графики по способу построения
Диаграмма представляет собой чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков. В свою очередь диаграммы имеют свою классификацию.
1. Диаграммы сравнения чаще всего представлены столбиковыми или ленточными диаграммами (гистограммами), круговыми, квадратными, фигурными и т.д. Эти диаграммы могут быть как плоскостными, так и объемными. Среди них наиболее популярны столбиковые диаграммы — рисунки в виде столбиков, высота которых соответствует значениям изучаемого показателя (рис. 3.3).
При построении столбиковых диаграмм необходимо соблюдать следующие требования:
Разновидностью столбиковой диаграммы является ленточная диаграмма, которая представляет собой рисунок в виде горизонтально вытянутых прямоугольников (лент). Принцип ее построения тот же, что и столбиковых диаграмм, только масштабной шкалой здесь служит горизонтальная ось (рис. 3.4).
Рис. 3.3. Гистограмма сравнения преимуществ PR-кампании в сети
Как столбиковые, так и ленточные диаграммы можно применять не только для сравнения самих величин, но и их составных частей, т.е. структуры.
В отличие от столбиковых и ленточных диаграмм в круговых, квадратных, прямоугольных и треугольных диаграммах величина изображаемого явления выражается размером площади, которая отводится этому показателю на поле графика, а сами графики строятся тоже по определенным правилам.
Например, для построения квадратной диаграммы для графического сравнения общего размера площади однокомнатной (35,2 м 2 ) и двухкомнатной (46,4 м 2 ) квартир вначале извлекаем квадратный корень из сравниваемых величин (получаем 5,9 и 6,8), затем выбираем масштаб (примем 1 см за 2 м 2 ) и отмечаем на графике стороны квадратов, пропорциональные полученным числам (рис. 3.5).
Круговые диаграммы, используемые для сравнения показателей, строят по тем же правилам. Разница лишь в том, что на графике вычерчиваются круги, площади которых пропорциональны квадратным корням из изображаемых величин, и при построении учитывается радиус окружности.
Рис. ЗА. Рейтинг магазинов по результатам опроса населения, проведенного независимой экспертной группой в декабре 2010 г.
Рис. 3.5. Квадратная диаграмма сравнения общей площади квартир
В треугольной диаграмме нужно так выбрать стороны и высоту треугольника, чтобы его площадь соответствовала величине показателя.
В качестве знаков для графика можно применять фигуры. Размер рисунка должен соответствовать величине показателя. Фигурные или картинные диаграммы <пиктограммы)усиливают наглядность изображения, так как включают рисунок изображаемого показателя (рис. 3.6).
Рис. 3.6. Фигурная диаграмма потребления кофе на душу населения
Структурные диаграммы характеризуют состав статистических совокупностей, для этой цели служат уже упомянутые выше столбиковые, ленточные диаграммы (рис. 3.7 и 3.8), а также секторные. Наиболее распространенным способом графического изображения структуры статистической совокупности является секторная диаграмма (рис. 3.9). При ее построении вся совокупность и соответствующая ей общая площадь круга принимается за 100%. Круг разбивается на секторы пропорционально частям совокупности. Поскольку на 1% приходится 3,6°, то для изображения любой части целого необходимо ее процентное выражение умножить на 3,6°.
Рис. 3.7. Столбиковая диаграмма структуры внутрироссийской миграции
3. Диаграммы динамики используются для изображения явлений, протекающих во времени. В данном случае используются линейные (рис. 3.10) и радиальные диаграммы (рис. 3.11).
Для построения линейных диаграмм обычно применяется прямоугольная система координат. На оси абсцисс откладываются варианты изучаемого показателя (или показания времени), а на оси ординат — величины изучаемого показателя. Зная эти координаты, легко определить положение каждого уровня на поле графика в виде соответствующей точки. Точки в линейных диаграммах являются геометрическими знаками. Последовательно соединяя найденные точки отрезками линий, получают эмпирическую линию графика, называемую статистической кривой. По виду этой линии можно судить о тенденциях и особенностях развития изучаемого явления в пространстве или во времени.
Радиальные диаграммы, построенные в полярной системе координат, применяются для отражения процессов, неоднократно повторяющихся во времени, и бывают двух видов: замкнутые и спиральные.
При построении таких диаграмм изображается окружность, которая делится на несколько равных частей по числу отрезков времени. Полученные точки деления соединяются с центром круга радиусами. На каждом радиусе в соответствии с выбранными промежутками времени и масштабом откладываются значения изучаемого показателя и полученные точки соединяются отрезками прямой. Получается ломаная линия, которая позволяет проследить динамику изучаемого явления.
Рис. 3.8. Ленточная диаграмма распределения населения России по возрастно-половому составу на 1 января 2010 г.
Рассмотрим построение радиальной замкнутой диаграммы на условном примере (по данным табл. 3.7).
Объем производства кондитерских изделий в России в 2010 г., тыс. т
Делим круг на 12 частей (соответственно числу месяцев в году), на радиусах согласно масштабу делаем отметки исходя из приведенных данных за каждый месяц. Получаем ломаную линию, которая позволяет проследить динамику изучаемого явления в течение года (рис. 3.11).
Рис. 3.9. Объемная секторная диаграмма долей предприятий на рынке мясной продукции Москвы и Московской области за 2010 г.
Рис. 3.10. Линейная диаграмма динамики производства муки в России за 1965—2011 гг.
Рис. 3.11. Радиальная замкнутая диаграмма производства кондитерских изделий в России по месяцам года в 2010 г., тыс. т
Спиральная радиальная диаграмма строится в том случае, если имеются помесячные статистические данные за ряд лет. Принцип се построения тот же, что и замкнутой диаграммы, но в ней декабрь одного года соединяется с январем не того же года, а с январем следующего года, так что получается кривая в форме спирали.
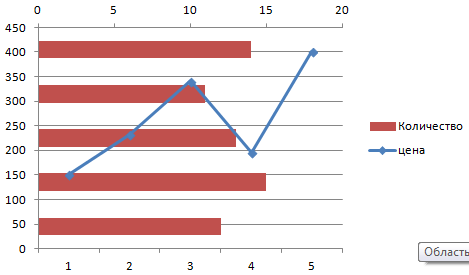
4. Диаграммы выявления взаимосвязи показателей явления. В экономической практике для сопоставления двух величин используется линейная и точечная диаграммы (рис. 3.12). Точечные диаграммы позволяют выявить прямую (положительную, когда с увеличением одного показателя происходит увеличение другого показателя) и обратную (отрицательную, когда с увеличением одного показателя происходит уменьшение другого показателя) зависимость двух параметров, а также отсутствие взаимосвязи между ними.
Рис. 3.12. Точечный график
Для сопоставления трех величин, из которых одна является произведением двух других, нередко применяются диаграммы под названием «знак Варзара» — это прямоугольник, у которого один сомножитель принят за основание, другой — за высоту, а вся площадь равна произведению (рис. 3.13). Так можно изобразить, например, размер посевной площади пшеницы в стране, величину урожайности и величину валового сбора в определенном году, а также, например, цену, количество продукции в натуральном выражении и выручку от реализации продукции (объем продаж).
Рис. 3.13. Знак Варзара, отображающий объем продаж
Статистические карты делятся на картограммы и картодиаграммы.
1. На картограмме распределение изучаемого признака по территории изображается условными знаками (точками, штриховкой, цветом и т.д.), соответствующими определенной интенсивности значений величины этого признака. Эти знаки покрывают площадь каждого района. Картограмма применяется в тех случаях, когда возникает необходимость показать территориальное распределение какого-нибудь одного статистического признака между отдельными районами для выявления закономерностей этого распределения (рис. 3.14).
Картограммы бывают фоновыми и точечными. На фоновых карто- граммах распределение изучаемого явления на территории изображается различными окрасками территориальных единиц с разной густотой цвета или штриховкой различной интенсивности. Чем более интенсивно явление, тем гуще штриховка или темнее окраска. Такие картограммы обычно используются для изображения уровня относительных и средних величин по территориям.
На точечной картограмме символами графического изображения статистических данных являются точки. Точечная картограмма применяется для размещения абсолютных величин. Каждой точке, нанесенной на картограмму, придается числовое значение, что позволяет использовать ее для прямого счета. Например, имеются четыре района с добычей угля в 200 тыс., 500 тыс., 1000 тыс. и 1400 тыс. т в год. Для составления картограммы примем точку за 100 тыс. т и нанесем на контур каждого района соответствующее количество точек.
Картограммы дают возможность графически отразить более сложные статистико-географические соотношения, чем картограммы. Так, при помощи картодиаграммы можно выразить пространственную специфику в структурах изучаемых статистических совокупностей, особенности каждого района как единого целого и т.д. В качестве диаграммных знаков в картодиаграмме часто используют различные геометрические фигуры, особенно круги, которые наиболее просты и удобны для выражения сравниваемых количественных показателей на карте.