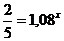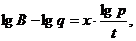Как сделать графики в маткаде

Построение графиков в MathCad

В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:

Построение графика по точкам

Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)

Рис. 1. Создание матриц-столбцов

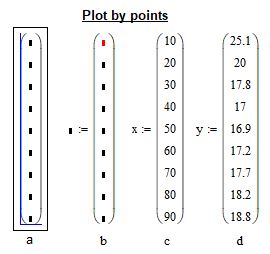
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «:«. У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.

Рис. 2. Заполнение матриц-столбцов для графика

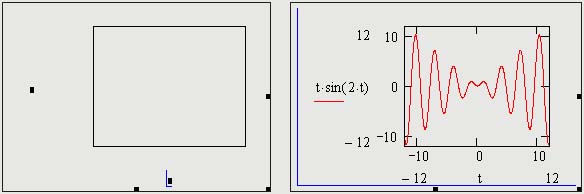
На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)

Рис. 3. Создание заготовки для графика

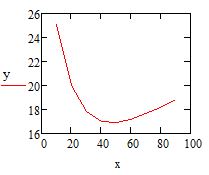
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)

Рис. 4. График по точкам

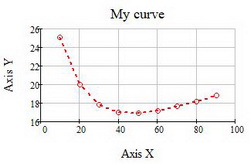
Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)

Рис. 5. Настройка отображения графика

Построение графика функции f(x)

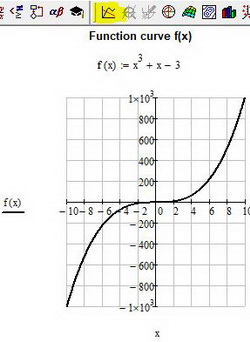
Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой

Рис. 6. Построение графика функции f(x)

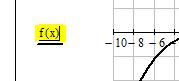
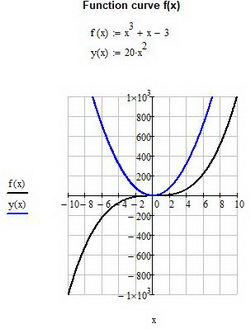
Рис. 7. Построение двух графиков функции

Построение эпюры в mathcad

Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:

— ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
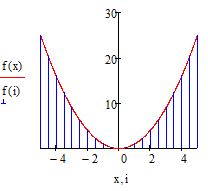
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании

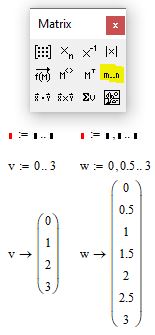
Рис. 8. Ввод ранжированной переменной

Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже

Рис. 9. Ввод ранжированной переменной

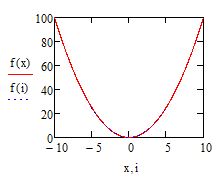
Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже

Рис. 10. Построение эпюры. Шаг 1

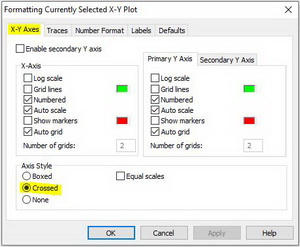
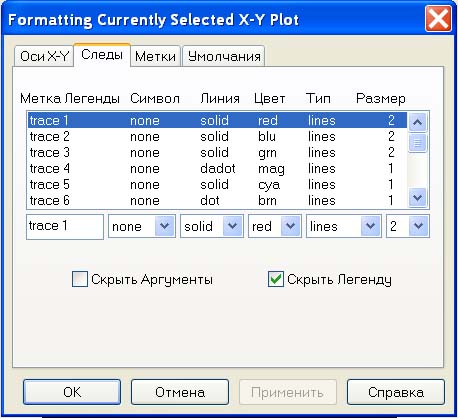
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.

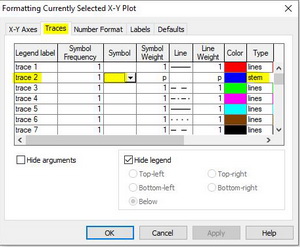
Рис. 11. Построение эпюры. Шаг 2

В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)

Рис. 12. Построение эпюры. Шаг 3

Построение графика в полярных координатах в mathcad

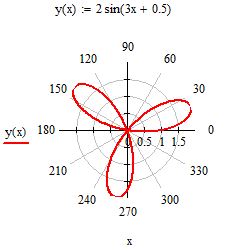
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)

Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph

Рис. 13. Создание загатовки для графика в полярных координатах

Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.

Рис. 14. Построение графика в полярной системе координат

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Источник

Как сделать графики в маткаде

Построение графиков в Mathcad

Для построения графиков в Mathcad можно воспользоваться функцией Вставка > График > Тип графика или панелью инструментов График (рис. 1.11). Поддерживаются следующие типы графиков:

При выборе режима построения двумерного графика в координатных осях Х-У на рабоче листе создается шаблон (на рис. 1.12 слева) с полями-заполнителями для задания отображаемых данных по осям абсцисс и ординат (имена аргументов и функций или выражения для них, а также диапазоны изменения значений). Заполнитель у середины оси координат предназначен для переменной или выражения, отображаемого по этой оси. Заполнители для граничных значений появляются после ввода аргумента и/или функции. Граничные значения по осям выбираются автоматически в соответствии с диапазоном изменения величин, но их можно задать, щелкнув в области соответствующих полей-заполнителей и изменив значения в них.

В правом фрагменте рис. 1.12 показан заполненный параметрами шаблон, причем диапазоны значений по осям определены вручную. Отметим, что эти значения видны только в режиме редактирования графика (наличие углового курсора на рисунках свидетельствует, что блок с графиком в данный момент выделен).

По оси абсцисс можно отложить простую переменную, задав для нее граничные значения (как на рис. 1.12), диапазон (о формировании диапазонов см. раздел «Работа с матрицами»), вектор значений. В заполнителях у оси ординат обычно помещают функции, выражения или векторы. На рис. 1.13 значения аргументов и трех функций размещены в столбцах двумерной ьатрицы. На графике отображены значения элементов из соответствующих столбцов.

В одной графической области можно построить несколько графиков. Для этого надо у соответствующей оси перечислить несколько выражений через запятую (см. рис. 1.13).

Аналогичным образом строится и форматируется график в полярных координатах, а для графиков других типов предварительно следует создать матрицы значений координат точек.

Для построения простейшего трехмерного графика, необходимо задать матрицу значений. Отобразить эту матрицу можно в виде поверхности, столбчатой диаграммы или линий уровня. Для отображения векторного поля значения матрицы должны быть комплексными. В этом случае в каждой точке графика отображается вектор с координатами, равными действительной и мнимой частям элемента матрицы. Во всех этих случаях после создания области графика необходимо указать вместо заполнителя имя матрицы, содержащей необходимые значения.

Для построения параметрического точечного графика командой требуется задать три вектора с одинаковым числом элементов, которые соответствуют х-, у- и z-координатам точек, отображаемых на графике. В области графика эти три вектора указываются внутри скобок через запятую. Аналогичным образом можно построить поверхность, заданную параметрически. Для этого надо задать три матрицы, содержащие, соответственно, х-, у- и z-координаты точек поверхности. В шаблоне в области графика эти три матрицы указываются в скобках через запятую.

Таким образом, можно построить практически любую криволинейную поверхность, в том числе с самопересечениями.

Источник

Урок 9. 3D-графики функций в Mathcad

Графики двух переменных в PTC Mathcad схожи с 2D-графиками. Однако существуют различия, о которых следует знать. В PTC Mathcad есть два типа 3D-графиков:

Контурный график

Контурный график отражает изменение поверхности по высоте. Он представляет собой линий равных высот. Чтобы вставить контурный график, выберите Графики –> Кривые –> Вставить график –> Контурный график:

Построим график параболоида:

Функция имеет минимум в начале координат и возрастает при увеличении расстояния от начала координат. Цвет графика зависит от величины функции z:

Попробуйте использовать кнопки для управления видом графика в левом верхнем углу, потом нажмите «Сброс вида».

Щелкните по оси Z на кнопке выбора оси. Измените значение последней (верхней) метки с 200 на 400, затем щелкните по пустой области, чтобы посмотреть, что получилось. Если нужно изменить значение обратно на 200, то нужно сделать это вручную – кнопка сброса вида здесь не сработает.

На втором графике мы изменили цвет графика и добавили заливку поверхности. Попробуйте сделать это с помощью меню Графики –>Стили:

Две функции

Чтобы добавить график второй функции, поместите курсор на местозаполнитель с легендой и нажмите Графики –> Кривые –> Добавить кривую. Ниже мы построили графики параболоида и плоскости:

Для графиков выбрали контрастные цвета, чтобы можно было увидеть их пересечение. Повращайте график, чтобы изучить форму этого пересечения.

Использование вектора

Мы строили 2D-графики с помощью векторов. Нечто похожее можно проделать для 3D-графиков, но нужен вектор со значениями по осям X, Y и Z. Мы показали это на примере функции, известной под названием «Мексиканская шляпа»:

Сфера

Построить параметрическую поверхность несколько сложнее, чем 2D-график, так как Вы можете добавить лишь значение Z на график. Мы проиллюстрируем, как это сделать на примере построения графика сферы с помощью функции CreateMesh. Параметрические уравнения сферы:

Матрица для построения поверхности формируется функцией CreateMesh:

Поместите имя переменной-матрицы в местозаполнитель 3D-графика. и щелкните по пустой области, чтобы увидеть результат:

Резюме

Трехмерные графики имеют некоторые существенные отличия от двухмерных графиков, рассмотренных в предыдущих уроках:

Источник

Сглаживание графика в MathCad

В Маткаде присутствует возможность применить к графику сглаживание, даже если он строился по малому количеству точек. Итог смотрите на рисунке ниже, а ход действий здесь.

Создаете две матрицы, обозначенные gx и gy, каждая с одним столбцом при помощи значка [::] с панели Matrix (для включения панели идите во View-Toolbars->Matrix). Это опорные точки, затем вводите переменную x с шагом 0.1, например. Это надо делать обязательно при помощи панели Matrix, не пытайтесь просто печатать две точки, выдаст ошибку.

Как построить график функции

Задачи для самостоятельного решения

ПРАКТИЧЕСКАЯ РАБОТА № 6

«Решение содержательных задач из различных областей науки и практики».

1) Обобщить теоретические знания по теме: подготовка к ЕГЭ по математике. Решение содержательных задач из различных областей науки и практики. Интерпретация, учёт реальных ограничений.

2) Рассмотреть алгоритмы решений заданий теме « подготовка к ЕГЭ по математике. Решение содержательных задач из различных областей науки и практики.», решить задачи.

3) Формировать умение ставить цели и реализовывать их.

Ход работы:

Используя теоретический материал, представленный ниж, выполните задания своего варианта.

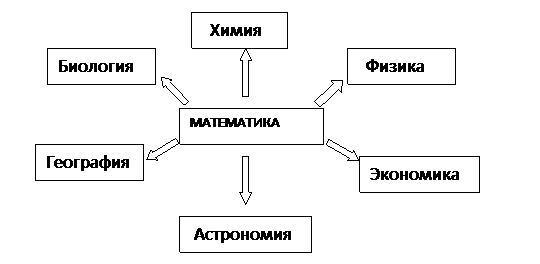
Современный мир неожиданно обнаружил, что математика уверенно расположилась в самых разных его частях и уголках. Сейчас никого не удивишь словосочетаниями «математическая лингвистика», «математическая биология», «математическая экономика» и т.п. — какую дисциплину ни взять, вряд ли кому-нибудь покажется невозможным присоединение к ее наименованию эпитета «математический». Распространение математики вширь сопровождается се проникновением вглубь. Математика занимает сегодня видное место в жизни общества.

Сферу приложения математики мы можем увидеть из схемы:

Математика и физика.

В физике широко распространена показательная функция:

p = p ₀ e – h / H

— Движение тела в сопротивляющейся среде:

— Радиоактивный распад:

Задача:

Решение:

Требуется найти момент времени t, когда R₁(t)-R₂(t)=25. Получаем уравнение:

(4/5) t /10 – (64/100) t /10 =1/4;

(4/5) t /10 – (16/25) t /10 =1/4;

(4/5) t /10 – (4/5) 2 t /10 =1/4.

Решая это уравнение, получаем у=½, т.е (4/5) t /10 =½. Логарифмируя по основанию 10, получим t/10 * lg 0,8 = lg ½, откуда t=10(-lg2)/3*lg2-1=31,06, т.е t=31,06.

Ответ: Через 31,06 минут.

Решение:

Подставим в данную формулу известные данные, получим:

— скорость химической реакции изучает раздел кинетика;

Приведем примеры решения данных типов задач.

Решение:

3 x =59000; lg 3 x = lg 59000; x lg3 =lg 59000;

Ответ: Надо повысить температуру на 100° для ускорения химической реакции.

2) Реакция при температуре 50°С протекает за 2 мин. 15 сек. За сколько времени закончится эта реакция при температуре 70°С, если в данном температурном интервале температурный коэффициент скорости реакции равен 3?

Решение. При увеличении t с 50° до 70° С скорость реакции в соответствии с правилом Ван-Гоффа возрастает:

Где t₂ = 70° С, t₁=50°C, а υ_t2 и υ_t1– скорости реакции при данных температура.

= 3 (70-50)/10 = 3 2 = 9

т.е. скорость реакции увеличится в 9 раз.

В соответствии с определением, реакция обратно пропорциональна t реакции, следовательно

,

где τ – время реакции при температуре t₁ и t₂, следовательно τ _t2 = τ _{t1 *} υ_t1/ υ_t2

Учитывая, что τ _t1= 135 сек., определяем t при 70°С: τ _t2= 135 * 1/9 = 15 сек

Ответ: τ _t2=15 сек.

Математика и биология.

Рассмотрим такие задачи:

1) Численность популяции составляет 5 тыс. особей. За последнее время в силу разных причин (браконьерство, сокращение ареалов обитания) она ежегодно сокращалась на 8%. Через сколько лет (если не будут предприняты меры по спасению данного вида и сохранятся темпы его сокращения) численность животных достигнет предела – 2 тыс. особей, за которым начнётся вымирание этого вида?

Решение: Применим для вычисления времени формулу сложных процентов: где

2 тыс. – численность животных по истечению искомого времени;

5 тыс. – численность животных в начальный момент времени;

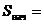
Предварительно разделив обе части уравнения на 1000, получим:

лет.

Ответ: Приблизительно через 11 лет.

2) Рассмотрим задачу об органическом росте в общем виде.

Пусть в начальный момент времени имелось q единиц некоторого компонента. В некоторый другой момент времени t имеющийся компонент изменился в p раз. Установите, через какой промежуток времени (начиная с начального момента) этот компонент достигнет заданного количества B единиц.

Решение: Для того чтобы это сделать, сначала напомним, что процессы, у которых происходит быстрый рост или быстрое затухание, описываются показательной функцией вида .

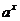
В нашем случае будем считать, что начальный момент времени соответствует нулю, тогда , и значит, , т.е. функция, описывающая этот процесс, имеет вид . В следующий момент времени t у нас произошли изменения, описываемые уравнением , т.е. , откуда

Таким образом, по данным условия мы получаем функцию . И теперь ясно, что мы ищем x, при котором , т.е. надо решить уравнение Выполняя логарифмирование уравнения по основанию 10, получим

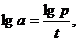
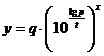
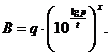
Ответ:

Математика и экономика.

1)Заглянем в кабинет экономиста одного из торговых предприятий. Перед которым возникла проблема – в каком соотношении закупить товары А и В. Можно закупить 8 единиц товара А и 5 единиц товара В. Торговое предприятие остановилось на первом варианте, т.к. при этом экономится сумма, достаточная для закупки 2-х единиц товара А. Какова цена товара А и товара В? Математика, выручай!

Пусть стоимость единиц товара А – х рублей, единиц товара В – у рублей. Тогда мы получим систему уравнений:

Решив которую, получим, что стоимость одной единицы товара А-12 тысяч рублей, а цена одной единицы товара В-4 тысячи рублей.

Решение: Обозначим через х млн.рублей прибыль первого отдела и через у млн.рублей прибыль второго отдела в минувшем году. Тогда по условию задачи составим и решим систему уравнений с двумя переменными:

Решив которую, получим, что:

1)прибыль в минувшем году у первого отделения 8 млн.рублей, у второго-5 млн.рублей.

2)Прибыль в этом году у первого отделения 14 млн.рублей, у второго-12 млн.рублей.

3)А теперь заглянем в кабинет экономиста некоторой фирмы, которая производит детские велосипеды. Экономисты рассчитывают, сколько велосипедов в день надо производить по цене х рублей, чтобы прибыль была максимальной. И в этот раз нам не обойтись без математики…

Решение: Изначально надо установить зависимость между ценой х руб. одного велосипеда и количеством у единиц товара, приобретаемого за один день. Математическими методами было определено, что данная зависимость задана формулой у=570-3х. (1) Выясним, какую цену на товар установит фирма для того, чтобы прибыль от его реализации была наибольшей. Прибыль р находится по формуле р=ху. Согласно (1), р=х(570-3х), или р=-3х2+570х. Таким образом получается, что функция р=-3х2+570х является квадратичной. Функция будет достигать своего наибольшего значения при х=-570/(-3)*2=95.

Это наибольшее значение равно р=27075. Получается, что наибольшая выручка в 27075 рублей будет достигаться в том случае, если фирма реализует по цене 95 р. у=570-3*95=285 единиц товара.

Источник