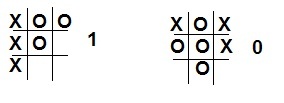Как сделать игру крестики нолики
Быстрый старт с Java: пишем «крестики-нолики»
Перед прочтением данной статьи рекомендую ознакомиться с предыдущей, «Быстрый старт с Java: начало», поскольку ожидается, что читатель владеет материалом, изложенным в ней — знает о переменных, условиях, циклах и импорте классов. Сегодня мы углублим знания о Java, создавая игру «Крестики-нолики», которая работает в командной строке (консоли). В процессе будет рассмотрена работа с массивами, а также некоторые аспекты объектно-ориентированного программирования (нестатические методы, нестатические поля, конструктор).
Массивы
При написании игры используется массив, поэтому давайте для начала рассмотрим, что это. Массивы хранят набор однотипных переменных. Если переменная похожа на коробочку, с написанным на боку типом, именем и со значением внутри, то массив похож на блок таких коробочек. И тип, и имя у блока одно, а доступ к той или иной коробочке (значению) происходит по номеру (индексу).
Методы
Решение одно — создать объект на основании класса. И затем вызывать метод через точку после имени объекта. В этом случае метод может быть нестатическим. Представленный ниже код это иллюстрирует.
Поля класса
Переменные существуют в рамках лишь того метода, где они объявлены. А если нужна переменная, доступная во всех методах класса, то пришло время использовать поля. Поля объявляются подобно переменным, с указанием типа и имени. Но располагаются они не в методах, а прямо в теле класса. Подобно методам, они могут быть статическими и нестатическими. Нестатические поля, как и методы, доступны только после создания объекта.
Крестики-нолики. Шаблон класса
Приступим к написанию кода игры. Начнём с шаблона класса и определения нужных полей. Именно это содержит приведённый ниже код. Первые две строки — импорт классов. Первыми в теле класса идут описания полей, затем методов. Метод main() используется для создания объекта (так как поля и методы нестатические) и вызова метода game() с игровой логикой.
Имена методов принято писать с маленькой буквы. Однако в коде мы видим метод TicTacToe() — есть ли тут нарушение? Нет, поскольку этот метод особенный и в объектно-ориентированном программировании называется конструктор. Конструктор вызывается сразу после того, как объект создан. Его имя, как видим, должно совпадать с именем класса. Мы используем конструктор для инициализации полей.
Игровая логика
Реализация вспомогательных методов
Заключение
На всякий случай прилагаю мой telegram — @biblelamp. Если вас заинтересовала тема, рекомендую почитать «Java-программирование для начинающих» Майка МакГрата и «Изучаем Java» Кэти Сьерра и Берт Бейтс.
Другие статьи из серии «Быстрый старт с Java»:
Если язык Java вас заинтересовал — приглашаем на факультет Java-разработки. Если ещё не совсем уверены — посмотрите истории успеха наших Java-выпускников:
Перед прочтением данной статьи рекомендую ознакомиться с предыдущей, «Быстрый старт с Java: начало», поскольку ожидается, что читатель владеет материалом, изложенным в ней — знает о переменных, условиях, циклах и импорте классов. Сегодня мы углублим знания о Java, создавая игру «Крестики-нолики», которая работает в командной строке (консоли). В процессе будет рассмотрена работа с массивами, а также некоторые аспекты объектно-ориентированного программирования (нестатические методы, нестатические поля, конструктор).
Массивы
При написании игры используется массив, поэтому давайте для начала рассмотрим, что это. Массивы хранят набор однотипных переменных. Если переменная похожа на коробочку, с написанным на боку типом, именем и со значением внутри, то массив похож на блок таких коробочек. И тип, и имя у блока одно, а доступ к той или иной коробочке (значению) происходит по номеру (индексу).
Методы
Решение одно — создать объект на основании класса. И затем вызывать метод через точку после имени объекта. В этом случае метод может быть нестатическим. Представленный ниже код это иллюстрирует.
Поля класса
Переменные существуют в рамках лишь того метода, где они объявлены. А если нужна переменная, доступная во всех методах класса, то пришло время использовать поля. Поля объявляются подобно переменным, с указанием типа и имени. Но располагаются они не в методах, а прямо в теле класса. Подобно методам, они могут быть статическими и нестатическими. Нестатические поля, как и методы, доступны только после создания объекта.
Крестики-нолики. Шаблон класса
Приступим к написанию кода игры. Начнём с шаблона класса и определения нужных полей. Именно это содержит приведённый ниже код. Первые две строки — импорт классов. Первыми в теле класса идут описания полей, затем методов. Метод main() используется для создания объекта (так как поля и методы нестатические) и вызова метода game() с игровой логикой.
Имена методов принято писать с маленькой буквы. Однако в коде мы видим метод TicTacToe() — есть ли тут нарушение? Нет, поскольку этот метод особенный и в объектно-ориентированном программировании называется конструктор. Конструктор вызывается сразу после того, как объект создан. Его имя, как видим, должно совпадать с именем класса. Мы используем конструктор для инициализации полей.
Игровая логика
Реализация вспомогательных методов
Заключение
На всякий случай прилагаю мой telegram — @biblelamp. Если вас заинтересовала тема, рекомендую почитать «Java-программирование для начинающих» Майка МакГрата и «Изучаем Java» Кэти Сьерра и Берт Бейтс.
Другие статьи из серии «Быстрый старт с Java»:
Если язык Java вас заинтересовал — приглашаем на факультет Java-разработки. Если ещё не совсем уверены — посмотрите истории успеха наших Java-выпускников:
Игра «Крестики-нолики» своими руками
Татьяна Пиманова
Игра «Крестики-нолики» своими руками
Хочу показать вам, как сделать интересные настольные игры для детей своими руками.
Одна из простых детских игр – это «крестики — нолики». Нужно — поле и 5 фишек на каждого игрока.
Это актуально особенно тогда, когда ребенок ещё не умеет хорошо рисовать.
Цель: Развивать логическое мышление у детей дошкольного возраста, развивать внимание, память, умение сосредотачиваться на определенном предмете довольно длительное время, обучить ребят различать такие понятия, как «по диагонали», «вертикально», «горизонтально», систематизировать знания, полученные ранее.
И вот несколько вариантов исполнения этой игры в разных материалах:
Самый простой вариант: нарисовать поле на бумаге и сделать крестикии нолики в крышках от пластиковых бутылок:
Этот вариант оценят девочки — такие милые сердечки,их можно вырезать из бумаги или сшить из фетра:
Так же вместо крестикови ноликов можно использовать обычные пуговицы:
Самый удобный и яркий вариант это играиз цветного картона в конверте:
этот вариант дети подготовительной группы сделали сами)
Дидактическая игра «Крестики-нолики» (вариант) «Крестики-нолики» – это игра из детства, до сих пор не потерявшая своей актуальности. Она не заставит вас заскучать! Цель игры:.
Дидактическая игра по ФЭМП «Математическая гусеница» своими руками Дидактические игры для своей группы,конечно,можно приобрести в магазине,но можно и смастерить самой своими руками,тем более сделать это.
Дидактическая игра, сделанная своими руками Дидактическая игра «Заколдованный городо» Задачи: Закрепить представления детей об архитектуре зданий и других сооружений родного города.
Дидактическая игра своими руками «Мемори» Наверняка многим знакома игра «Мемори». Это не только веселая, но и полезная развивающая игра – с ее помощью вы тренируете усидчивость,.
Дидактическая игра своими руками «Моя дружная семья» Представляю вашему вниманию дидактическую игру, которую я сделала своими руками, когда готовилась к открытому мероприятию по ознакомлению.
Дидактическая игра своими руками «Волшебный лес» Сделать развивающую игру из подручных средств очень легко, главное — найти нужный кусочек фетра. В моих руках как раз оказался такой. И.
Игра «Крестики-нолики» Доброе время суток уважаемые коллеги и гости моей странички. Игру «Крестики-нолики», наверно, знают абсолютно все. Эта игра проста и интересна.
Познавательная викторина для детей подготовительной группы «Крестики-нолики» с участием родителей Цель: создать в ходе совместной деятельности ситуацию успеха для каждого ребенка. Задачи: 1. Познакомить детей с новой игрой, учить принимать.
Развивающая игра для детей старшего дошкольного возраста «Крестики-нолики» Игра «Крестики- нолики» используется в группах для детей старшего дошкольного возраста. Цель: Способствует развитию внимания, памяти, логического.
Сюжетно-ролевая игра «Мореплаватель» своими руками Захотелось придумать что-то новенькое. Идею создать атрибуты для сюжетно-ролевой «Мореплаватели» навеяла шапочка моряка из нашего театрального.
Обучение с подкреплением на примере игры «крестики-нолики»
Поготовка
Примем следующие правила:
состояний. Конечно же, половина этих комбинаций невозможна, но и оптимизации кода в целях не стояло.
Ход игры
Оппонетном будет являться человек, который соответственно будет играть за нолики и периодически поддаваться. В ходе игры будет происходить изменение ценности ее состояний. Для того, чтобы правильно оценить действия агента, необходимо записывать последовательность тех состояний, которые он выбрал и по окончании игры перерасчитать их. Формула расчета ценности V(s) будет иметь следующий вид:
,
где А — размер шага, влияющего на скорость обучения. V(s’) — ценность действия по окончанию игры (1 — если выиграл, 0 — иначе).
Размер шага влияет на то, будет ли меняться стратегия оппонента или нет. Если необходимо учитывать изменчивость стратегии, то необходимо оставить размер шага константой. Иначе при уменьшении шага до нуля агент остановит свое обучение.
Использование зондирующих ходов (не имеющих высокую ценность) позволяет проверить состояния, которые ввиду высокой ценности других ходов никогда бы не исполнились, что дает небольшой шанс на изменение стратегии в выигрышную сторону.
В выше расположенном коде происходит отбор возможных ходов (состояния в которых элементы идентичны текущему состоянию поля, а также присутствует еще один крестик). Затем из полученных состояний выбирается либо произвольный ход (с вероятностью 5%), либо «жадный» ход (с максимальной ценностью). По окончании выбора, данный ход записывается в отдельный массив сделанных ходов.
По окончании игры происходит как уже сказано перерасчет ценности сделанных ходов.
В данном примере был кратко рассмотрен один из аспектов обучения с подкреплением. Если обычно агент контактирует со средой, то в данном примере обучение осуществлялось с игроком-противником. Хотя этот пример довольно прост, может показаться что данный метод на других примерах будет очень ограничен чем это есть на самом деле.
Простой алгоритм проверки победы в крести-нолики на не стандартном поле
Столкнулся с такой проблемой, что молодым программистам, которые только начинают изучение языков, алгоритмы вызывают больше трудностей, чем синтаксис языка. Если сам синтаксис и концепцию объяснит преподаватель по конкретному языку, то алгоритмы вам придется придумывать самим. Исключением из правил могут быть только специализированные технические специальности в ВУЗах, где преподают именно алгоритмы.
При том, что алгоритм решения может быт очень простым многие не знают как подойти к решению задачи. Я рассмотрю пример проверки победы в игре крестики-нолики, но на поле 6х6 и блоком подряд заполненных значений равному 4-м.
На самом деле, здесь представлен универсальный алгоритм, только вместо переменных я использовал константы. И это практически не зависит от языка, котором эта проверка осуществляется. Я предлагаю начинающим программистам сначала решить задачу графически, а затем уже перевести ее на тот или иной язык. Для создания этого алгоритма подойдет листок в клетку и ручка.
Итак, у нас есть поле 6х6.
Блок последовательно заполненных элементов, который достаточен, чтобы выиграть, равен 4-м.
Думаю, что теперь (всего лишь поле двух рисунков) стало намного понятнее, как решить эту задачу.
Фактически мы должны решить 2 независимые задачи:
1. Найти все заполненные последовательности в блоке 4х4
Почему проверяем блок 4х4? Все просто в нем возможно только 2 диагонали такой размерности, которая нам нужна.
Используя двоичную логику (1&1=1 и 1&0=0) мы можем легко сделать проверку циклами. Для этого нам нужна 1 переменная для каждой диагонали. Пусть toright – логическая переменная в которую пишем результат проверки диагонали сверху слева вниз направо. И toleft для проверки диагонали сверху справа вниз налево.
Первоначально выставим значение true для этих переменных. Дальше мы сравниваем каждую клетку в диагонали с символом «Х» или «О». Конечно, мы делаем это 2-мя вызовами либо все сравниваем с «Х», либо все с «О».
Каждую клеточку диагонали мы сравниваем с нашим символом и получаем результат (true) или (false). Затем делам логическую операцию (&) между полученным результатом и нашей toright. Результат этой операции пишем опять в toright. Если на каком-то этапе мы получим результат (false), то все дальнейшие toright всегда будут равны (false). Это следует из правила логических операций (1&0=0).
Напишем это на Jave:
Собственно вот в этой строчке
Краткая запись выглядит так:
Получаются только 2 результата работы условия:
Для 2-х диагоналей, полный код функции будет выглядеть так:
Полный аналог делается для проверки вертикалей и горизонталей, только циклы меняются.
Собственно это и есть решение для блока 4х4. Как видно из кода, для другого блока нужно только поменять 4 в цикле на другое число, или написать вместо числа имя переменной. Причем эту переменную вы можете сделать как глобальной видимости, так и передать в функцию, например так:
2. Найти все квадраты 4х4 в квадрате 6х6
Собственно, их не так много. Начиная с позиции [0,0], [1,0] и [2,0] для первой строки квадрата, [0,1], [1,1] и [2,1] для второй, [0,2], [1,2] и [2,2] для третьей. Дальше квадрат 4х4 выйдет за границы квадрата 6х6.
Такой перебор координат вполне можем сделать циклами:
Тут нам придется немного модифицировать методы checkDiagonal и checkLanes, поскольку мы должны проверять квадрат 4х4 с соответствующим смещением.
Начинающим программистам я бы рекомендовал самим модифицировать код checkDiagonal, т.к. это позволит лучше понять принцип работы.
И еще один совет. В настоящий момент имеется огромное количество реализаций различных алгоритмов в сети на разных языках. Если вы хотите научиться думать, то смотрите именно принципы решений (алгоритмы), не привязанные к языкам. Готовые решения не позволят вам быстро научиться выбирать наиболее оптимальный вариант решения. Очень часто, переписать готовое решение с одного языка на другой, можно не понимая принципа решения задачи. Где-то это вам поможет, а где-то может сделать дальнейшее развитие программы невозможным без изменения ее логики.
Сначала я рекомендую попробовать написать проверку самостоятельно. Шаблон игры можно забрать здесь. Там уже есть заголовки функций, которые я описал в статье. Осталось скопировать в шаблон часть моего кода и чуть-чуть его модифицировать. А вот здесь можно скачать полный рабочий код на Java. Рекомендую смотреть его уже после того, как вы написали свои функции на основе этой статьи.
Как выиграть в крестики-нолики
Каждый из нас хотя бы раз в жизни играл в знаменитые крестики-нолики, пытаясь построить в ряд или по диагонали 3 крестика или 3 нолика на девятиклеточном поле. Если вы достаточно тренировались в этой игре, то, наверняка, знаете, что два опытных игрока всегда заканчивают партию вничью, и это делает игру для них неинтересной. В этой статье вы прочитаете о том, как выиграть в крестики-нолики или, по крайней мере, не проиграть, а также узнаете все хитрости и секреты прохождения этой популярной игры.
Немного о правилах. Цель игры выстроить на девятиклеточном поле подряд 3 одинаковых фигуры (3 крестика или 3 нолика) по горизонтали, по вертикали или по диагонали раньше, чем это сделает ваш партнер по игре. Игра в крестики-нолики начинается с хода игрока, который ставит крестик в любой клетке на игровом поле три на три (отметим сразу, что у него гораздо больше шансов выиграть, чем у противника). После этого второй игрок ставит в любой свободной ячейке нолик. Затем снова ходит крестик. Потом опять нолик. И так продолжается до тех пор, пока:
Тактика крестиков
Первый ход крестиков. Самой выгодной позицией является середина игрового поля, или как отмечено на схеме клетка №5. Именно сюда следует вписывать вашу фигуру, если эта ячейка является свободной, и именно поэтому начинающие крестики всегда имеют преимущество. Через центральную ячейку вы можете построить наибольшее количество возможных вариантов выигрыша: две диагонали, одну горизонталь и одну вертикаль.
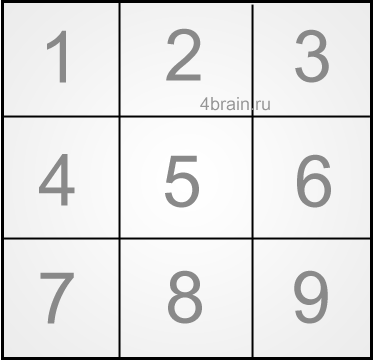
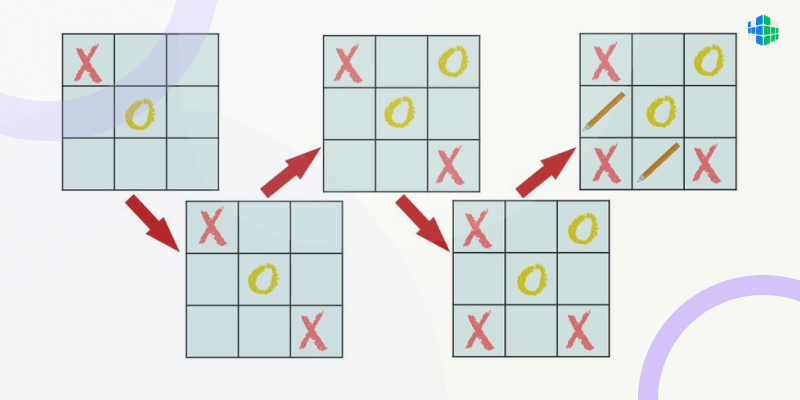
Второй ход крестиков. После того как вы сделали первый ход, поставив крестик по центру, вам остается ждать ход противника. В целом, у него есть всего 2 возможных варианта действий: поставить нолик в одной из «угловых» ячеек (№1, №3, №7 и №9) или поместить свою фигуру в ячейки №2, №4, №6 или №8. И следует сразу отметить, что от этого хода уже коренным образом зависит ваша возможность выиграть.
Если игрок выбирает одну из недиагональных ячеек №2, №4, №6 или №8, то у вас появляется беспроигрышная стратегия. Другими словами вы сможете победить с вероятностью 100%, если знаете, как верно действовать. Этот алгоритм описан в схеме ниже. В первую очередь вам нужно поставить крестик своим вторым ходом в угловую клетку, вынудив соперника защищаться. А после этого вы занимаете еще одну свободную угловую клетку, в результате чего вы имеете 2 ряда, где не хватает всего одного крестика (это показано на последнем поле схемы). Куда бы соперник ни поставил свой нолик, вы в любом случае побеждаете, имея запасную стратегию.
Если же ваш соперник своим первым ходом выбирает ячейки №1, №3, №7 и №9, тогда вы не имеете абсолютной выигрышной стратегии, и вам следует уповать лишь на дальнейшую невнимательность второго игрока, что в такой простой игре бывает достаточно редко.
Третий и последующие ходы крестиков. Дальнейшие ходы «крестиков» должны быть направлены на построение в ряд 3-х собственных фигур, а также на пресечение маловероятных, но все-таки возможных попыток «ноликов» поставить подряд 3 фигуры.
Также, «крестики» для того, чтобы выиграть могут начинать не только с центральной клетки, но и с угловой. Подробнее об этом читайте здесь.
Алгоритмы ходов ноликов
Если вам выпало играть ноликами, то в большинстве случаев вам предстоит бороться только за ничью. Однако у вас есть шансы победить, если вы играете с совсем неискушенным игроком.
Первый ход ноликов. Если игрок №1 почему-то не занял центральную клетку – смело ставьте туда нолик и действуйте дальше, опираясь на стратегию крестиков, описанную выше. Но, скорее всего, центральная ячейка к моменту вашего начального хода будет уже занята. В этом случае не совершайте непростительную ошибку и не ставьте нолик в ячейки №2, №4, №6 или №8, а выбирайте только диагональные ячейки №1, №3, №7 и №9.
Второй и последующие ходы. Дальнейшие ходы «ноликов» должны быть направлены на пресечение попыток «крестиков» поставить подряд 3 фигуры, а также при возможности, на построение в ряд 3-х ноликов, что является практически невозможным.
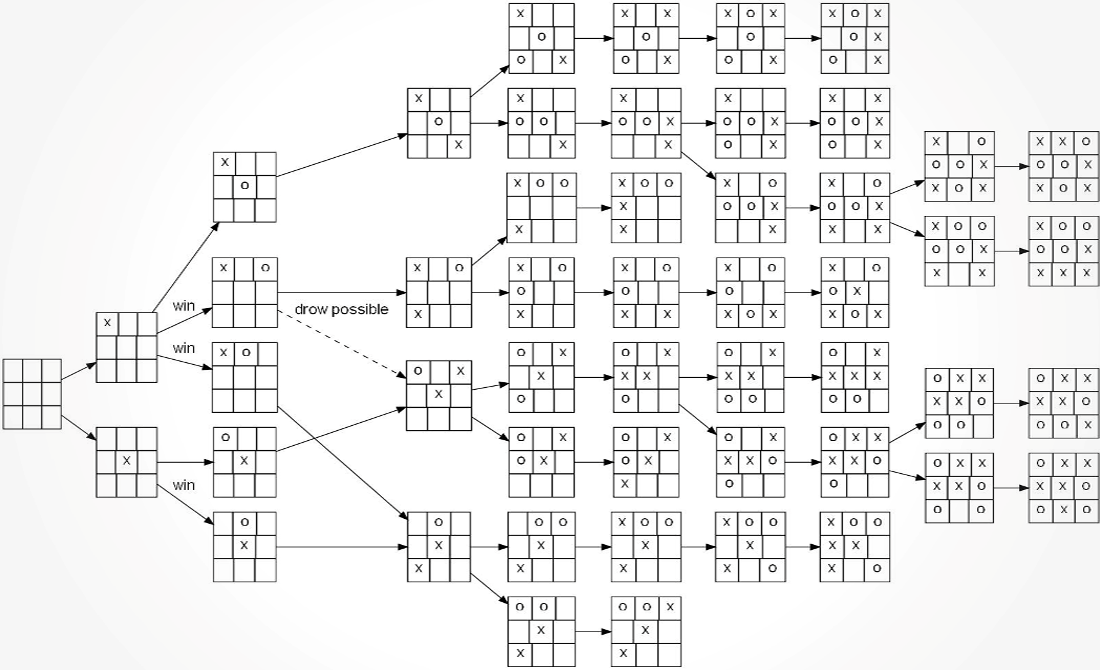
Все стратегии игры
На графике, представленном ниже, который можно найти в Википедии, приведены возможные стратегии побед и ничьих в игре крестики-нолики на поле в 9 клеток. 
Надеюсь, эта статья стала для вас помощником в хитростях крестиков-ноликов, в том числе на деньги и на раздевание, и вы теперь знаете некоторые необходимые тактики и стратегии для того, чтобы выиграть (или, по меньшей мере, не проиграть) в эту замечательную игру. А если у вас есть комментарии, отзывы и предложения – оставляйте их ниже.
Кроме того, рекомендуем ознакомиться с еще одной стратегией крестиков-ноликов 3 на 3 по ссылке.