Как сделать сферу в opengl
Как сделать сферу в opengl
Приводятся C#-функции, воспроизводящие средствами OpenTK-библиотек (OpenTK, OpenTK.Graphics.OpenGL, OpenTK.Input) сферу (рис. 1 и рис. 2).
Рис. 1. Сфера с нормалями
Рис. 2. Сфера без нормалей
Вид сферы в консоль-проекте определяется следующими переменными:
bool showTexture; // Выводим сферу с текстурой
bool useMaterial; // Используем материал и источники света
bool showNormals; // Показываем нормали
Если все перечисленные переменные равны false, то выводится чисто полигональная модель сферы.
Тонированное изображение будет сглаженным, если переменная
В противном случае вывод полигонов будет выполняться без интерполяции цветов.
Смена варианта вывода сферы обеспечивается клавишами F7, F8 и F9:
Текстура формируется на основе показанного на рис. 3 образа.
Сферы с текстурой и материалами сглаженная и без сглаживания показаны на рис. 4.
Рис. 4. Сферы с текстурой и материалами в режимах Smooth и Flat
Построение сферы
Нижеприводимая процедура обеспечивает:
Формирование текстуры
// Создает 2D-текстуру на базе растрового образа, загруженного в data
public void makeTxtr()
<
// Активизируем режим вывода текстуры
GL.Enable(EnableCap.Texture2D);
// Генерируем идентификатор текстуры
GL.GenTextures(1, out texture);
// Связываем текстуру с идентификатором
GL.BindTexture(TextureTarget.Texture2D, texture);
// Параметры текстуры
GL.TexParameter(TextureTarget.Texture2D, TextureParameterName.TextureMinFilter, (int)TextureMinFilter.Linear);
GL.TexParameter(TextureTarget.Texture2D, TextureParameterName.TextureMagFilter, (int)TextureMagFilter.Linear);
// Создаем текстуру
GL.TexImage2D(TextureTarget.Texture2D, 0, PixelInternalFormat.Rgba, data.Width, data.Height, 0,
OpenTK.Graphics.OpenGL.PixelFormat.Bgra, PixelType.UnsignedByte, data.Scan0);
>
Материал и свет
Весь код WindowsFormsApplication
namespace WindowsFormsApplicationOpenTK
<
public partial class FormSphere : Form
<
bool showNormals = false; // Флаг вывода нормалей
double sphR = 20; // Радиус сферы
int nx = 16; // Число разбиений сферы по X и Y
int ny = 16;
Весь код консоль-проекта
namespace SphereTest
<
public class SimpleWindow : GameWindow
<
double sphR = 2; // Радиус сферы
// Файл для текcтуры
static string path = «G:\\Шоя\\watch\\earth3.png»; // earth2 или 3 или 4.png
static Bitmap bitmap = new Bitmap(path);
BitmapData data;
int texture;
bool showTexture = false;
bool useMaterial = true;
bool showNormals = false;
bool flat = true;
Рисование сферы в OpenGL без использования gluSphere()?
10 ответов
При работе с glut я использовал glutsolidsphere для рисования своих сфер, но, перейдя на glfw, мне пришлось использовать glusphere. Я в основном скопировал всю функцию glutsolidsphere в свой собственный код, но получаю странную проблему освещения, где раньше меня не было. Вот код для сферы : void.
Как только у вас будет достаточное количество точек, вы нормализуете их векторы так, чтобы все они находились на постоянном расстоянии от центра твердого тела. Это приводит к тому, что стороны выпячиваются в форму, напоминающую сферу, с возрастающей гладкостью по мере увеличения количества точек.
Нормализация здесь означает перемещение точки таким образом, чтобы ее угол по отношению к другой точке был одинаковым, но расстояние между ними различалось. Вот вам двумерный пример.
A и B находятся на расстоянии 6 единиц друг от друга. Но предположим, что мы хотим найти точку на линии AB, которая находится на расстоянии 12 единиц от точки A.
Мы можем сказать, что C-это нормализованная форма B относительно A, с расстоянием 12. Мы можем получить C с помощью такого кода:
Если мы проведем этот процесс нормализации на множестве точек, все относительно одной и той же точки А и с одинаковым расстоянием R, то все нормализованные точки будут лежать на дуге окружности с центром а и радиусом R.
Здесь черные точки начинаются на линии и превращаются в дугу.
Этот процесс может быть расширен до трех измерений, и в этом случае вы получите сферу, а не круг. Просто добавьте компонент dz в функцию нормализации.

Если вы посмотрите на сферу в Epcot, вы можете как бы увидеть эту технику в действии. это додекаэдр с выпуклыми гранями, чтобы он выглядел более круглым.
Далее я объясню популярный способ генерации сферы с использованием широты и долготы (другой способ, икосферы, был уже объяснен в самом популярном ответе на момент написания этой книги.)
Сфера может быть выражена следующим параметрическим уравнением:
Генерация сферы затем включает в себя оценку параметрической функции через фиксированные интервалы.
Например, чтобы сгенерировать 16 линий долготы, вдоль оси u будет располагаться be 17 линии сетки с шагом π/8 (2π/16) (17-я строка оборачивается).
Следующий псевдокод создает треугольную сетку путем вычисления параметрической функции через равные промежутки времени (это работает для любой параметрической функции поверхности, а не только для сфер).
Код в этом примере быстро объясняется. Вы должны заглянуть в функцию void drawSphere(double r, int lats, int longs) :
Я экспериментировал с OpenGL, пытаясь нарисовать сферы внутри и снаружи прямоугольных призм. Проблема в том, что независимо от того, где я выбираю рисовать сферы, сетка всегда лежит поверх моих кругов, как видно ниже: То, что я делаю прямо сейчас, в основном использует glTranslatef для.
Если бы вы хотели быть хитрым, Как лиса, вы могли бы на полдюйма сдвинуть код с GLU. Проверьте исходный код MesaGL (http://cgit.freedesktop.org/mesa/mesa/).
Смотрите Красную книгу OpenGL: http://www.glprogramming.com/red/chapter02.html#name8 она решает проблему путем разбиения на полигоны.
Я знаю, что это немного не по теме, но я думаю, что это может помочь, если кто-то будет здесь искать этот конкретный случай.
Мой пример, как использовать ‘triangle strip’ для рисования сферы «polar», состоит в рисовании точек попарно:
Первая введенная точка (glVertex3f) соответствует параметрическому уравнению, а вторая смещена на один шаг Альфа-угла (от следующей параллели).
Один из способов состоит в том, чтобы сделать четырехугольник, обращенный к камере, и написать вершину и фрагмент shader, который визуализирует нечто, похожее на сферу. Вы можете использовать уравнения для круга / сферы, которые вы можете найти в интернете.
Одна приятная вещь заключается в том, что силуэт сферы выглядит одинаково с любого угла. Однако если сфера не находится в центре перспективного вида, то она, возможно, больше похожа на эллипс. Вы можете разработать уравнения для этого и поместить их в затенение фрагмента. Затем световое затенение должно изменяться по мере движения игрока, если у вас действительно есть игрок, движущийся в пространстве 3D вокруг сферы.
Может ли кто-нибудь прокомментировать, пробовали ли они это или это было бы слишком дорого, чтобы быть практичным?
Python адаптация ответа @Constantinius:
Похожие вопросы:
В основном я хочу вращающуюся землю 3d. Функция gluSphere не найдена. он доступен на iphone-х opengl-х годах? как я могу сделать сферу иначе?
Я использую OpenGL с C++ (но без шейдеров и GLSL) и рисую сферы (бильярдный шар) и цилиндры (Кий), используя функции библиотеки glu для их рисования. Я использую glBindTexture() для привязки.
У меня есть код для комнаты, предоставленной мне, мне нужно добавить сферу в комнате. Это выглядит так: PushMatrix(); //draw floor,walls,ceilings PushMatrix(); //draw some boxes on front wall.
При работе с glut я использовал glutsolidsphere для рисования своих сфер, но, перейдя на glfw, мне пришлось использовать glusphere. Я в основном скопировал всю функцию glutsolidsphere в свой.
Я экспериментировал с OpenGL, пытаясь нарисовать сферы внутри и снаружи прямоугольных призм. Проблема в том, что независимо от того, где я выбираю рисовать сферы, сетка всегда лежит поверх моих.
Мне нравится рисовать сферы в среде OpenGL, используя gluSphere(). Однако я хотел бы нарисовать границу вокруг сферы, причем граница представляет собой круг, идеально выровненный с рамкой камеры.
Я пытаюсь визуализировать сферу без использования функции gluSphere(). Но этот код не рендеринг какой-либо сферы. Я не могу точно определить, в чем заключается ошибка. import sys import math from.
Я пытаюсь нарисовать сферу в Matlab без использования функции сферы. Это мой код: r = 2; [ x,y ] = meshgrid(-4:0.1:4); z = sqrt(r^2-x.^2-y.^2); mesh(real(z)); hold on mesh(real(-z)); Приведенный.
В этом уроке мы нарисуем объёмные фигуры: куб, пирамида, сфера, конус, тор (плюшка), и включим освещение примитивов.
Сначала необходимо скачать (ссылка в конце урока) и подключить библиотеку DGLUT.pas.
Напомню, для того, что бы подключить библиотеку нужно ввести ее имя в секцию uses
В библиотеке DGLUT.pas записаны уже готовые алгоритмы построения объёмных фигур.
Например:
Алгоритм рисования куба вручную: При помощи библиотеки: В OpenGL есть буфер глубины, второе его название ZBuffer. В нем хранятся данные о расстоянии от каждого пиксела монитора до точек в объёмном пространстве OpenGL, принадлежащих этому пикселу. OpenGL выводит точки, расстояние до которых меньше всех расстояний до точек принадлежащие этому пикселу.
Удалите все примитивы прошлого урока в процедуре FormPaint и дополните её кодом: 
После компиляции мы увидим куб белого цвета. Белый, потому что он не освещается.
Что бы включить источник света, нужно добавить в функцию создания формы. Источников света не может быть больше 8.
Давайте скомпилируем и посмотрим, что получилось.

Куб стал смотреться более объёмно, благодаря освещению.
Таким образом, получится, что мировая система координат останется на месте, а система координат куба будет смещена.
Изменим код вывода куба: 
Вот сейчас, когда стало много места, можно нарисовать сферу функцией glutSolidSphere(радиус, кол-во сегментов по X, кол-во сегментов по Y) и сдвинем в противоположную сторону. 
Двигаемся дальше и рисуем тор функцией glutSolidTorus(радиус сечения, радиус окружности, кол-во сегментов по X,кол-во сегментов по Y) и сдвинем его от нас на 5 единиц пространства. 
Нарисуем додекаэдр функцией glutSolidDodecahedron и сдвинем его в нашу сторону. 
И наконец, нарисуем конус функцией glutSolidCone(радиус базы, высота, кол-во сегментов по X,кол-во сегментов по Y) и сдвинем его вверх на 2 единицы. 
Всё. Таким образом, процедура FormPaint должна содержать следующий код: В следующем уроке мы познакомимся с нормалями.
Уроки OpenGL. Часть 4. Создание 3D-объектов.
Продолжается цикл статей, посвященных работе с библиотекой OpenGL на нашем сайте, и, наконец, пришло время подключить третье измерение в наших экспериментах! Сегодня мы создадим в пространстве куб, а также добавим функцию вращения 3D-фигуры вокруг осей x и y. Как всегда разберем все по шагам, а в конце статьи я выложу полный проект с реализованным примером.
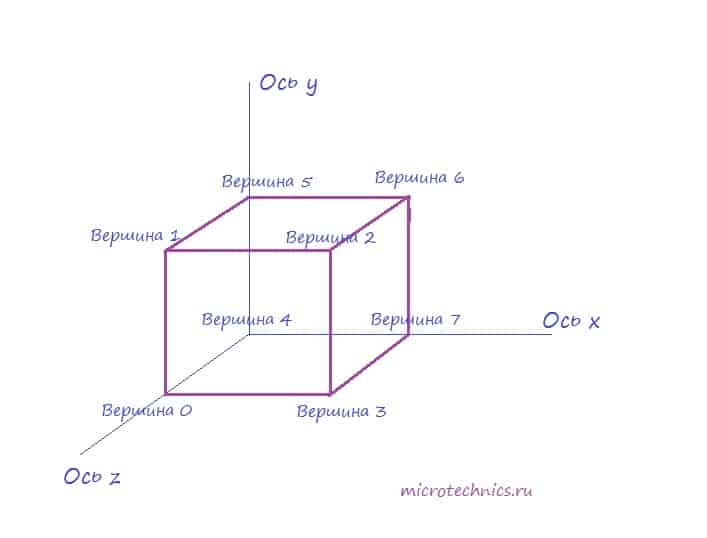
Что из себя представляет куб? Ответ прост – 6 граней (квадратов) и 8 вершин 🙂 Именно так мы и будем строить фигуру – построим по отдельности 6 его граней, а эта задача для нас уже не представляет никакой сложности. Но прежде, чем приступать к рисованию, добавим в функцию initializeGL() следующее:
Помните на прошлом уроке, когда мы задавали разные цвета вершин у одной фигуры, то получали красивые переходы между цветами. Так вот сегодня нам это не нужно, грани будут иметь однородный цвет и именно для включения этого режима (а точнее для отключения режима сглаживания цветов) мы вызываем первую из этих функций. Цвет грани у нас теперь будет определяться цветом последней(!) нарисованной вершины квадрата.
Вторая функция устанавливает режим, когда строятся только внешние поверхности фигур. И вот тут есть один важный момент. Для корректного отображения объекта вершины в массиве вершин должны задаваться против(!) часовой стрелки.
Собственно, с приготовлениями на этом заканчиваем, начинаем отрисовку. Нам понадобятся три массива:
С размерами массивов мы разобрались на прошлом уроке, не буду повторяться, поэтому сразу же переходим к заполнению их данными. Кстати ребро нашего куба будет равно единице, в соответствии с этим задаем координаты вершин в трехмерном пространстве:
Мы задали координаты и цвета вершин куба. Давайте для наглядности посмотрим на рисунок:
Номера вершин на рисунке полностью соответствуют тому, как мы их задали в нашей программе. Теперь, глядя на картинку можно с легкостью пройтись по всем 6 граням куба и заполнить массив индексов. Давайте смотреть:
Теперь тоже самое делаем в программе:
Теперь осталось только вызвать функцию рисования:
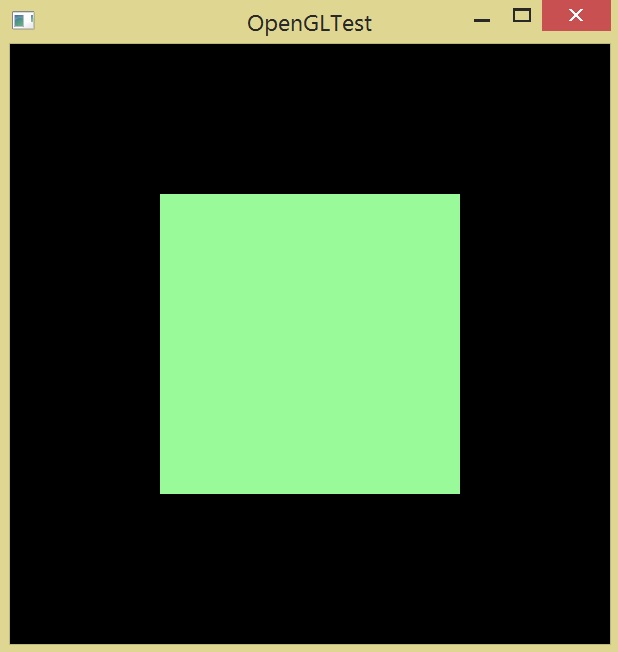
Запускаем программу и видим наш куб!
Правда на данный момент он больше похож на квадрат 🙂 Все потому что мы смотрим на куб со стороны оси z и видим его проекцию на плоскость X0Y. Для того, чтобы все-таки увидеть, что это действительно куб, давайте добавим возможность вращать фигуру при удержании кнопки мыши и перемещении ее указателя.
Сделаем так – при перемещении указателя мыши от левого края до правого будем поворачивать куб на 180 градусов. Осталось вычислить, на сколько градусов нужно повернуть фигуру при произвольном перемещении курсора. С этим все просто, получаем формулу:
Здесь d – это расстояние, на которое мы переместили курсор, w – ширина нашего окна. Обратите внимание, что при движении мыши вдоль оси x поворот будет осуществляться вокруг оси y, и наоборот, перемещение вдоль y – поворот вокруг x. Итак, сейчас нам нужно получить в программе данные о перемещениях мыши. Для этого переопределим методы:
При нажатии кнопки мыши ( mousePressEvent() ) сохраняем в переменную pressPosition текущие координаты курсора. При перемещениях указателя производим расчет углов поворота, на которые необходимо развернуть куб, а затем вызываем функцию updateGL() для перерисовки сцены в соответствии с полученными данными. Не забываем объявить все используемые методы и переменные в файле MainScene.h.
Функцию updateGL() то мы вызвали, но само собой ничего, естественно, не повернется 🙂 Для поворота 3D-фигуры OpenGL предлагает нам следующую функцию:
Здесь первый параметр – угол поворота, а три остальных определяют, вокруг какой из осей необходимо выполнить вращение. То есть если мы сделаем так:
То фигура повернется вокруг оси x на 45 градусов.
С этим все понятно, осталось только добавить вызов этой функций к нам в программу, а точнее в функцию paintGL():
Как видите, все оказалось довольно-таки просто!
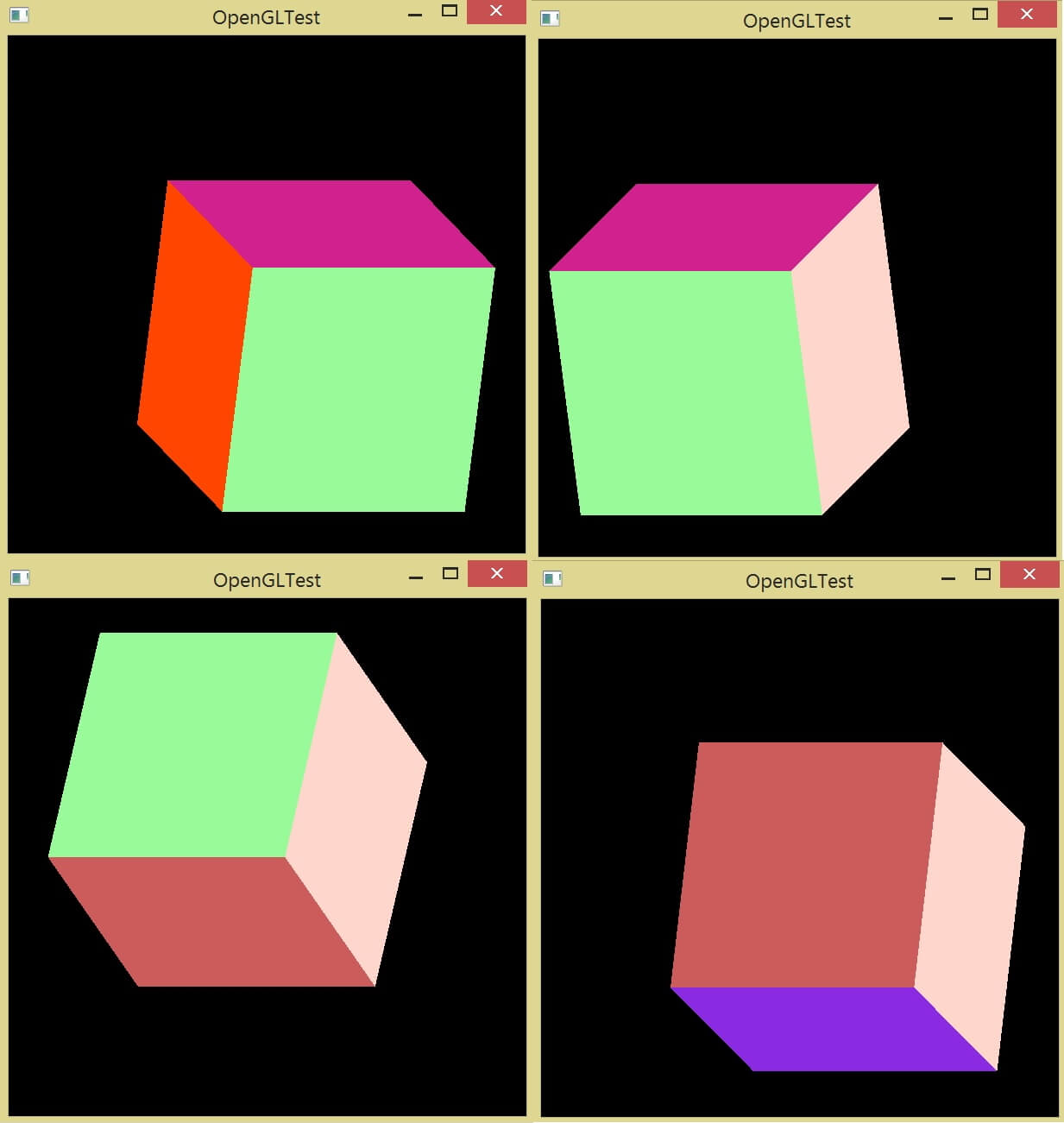
Теперь нам предстоит собрать проект и проверить результат:
На этом заканчиваем сегодняшнюю статью! А уже скоро, а именно в следующем уроке, мы разберемся с текстурами в OpenGL – создадим собственные текстуры и нанесем их на 3D-объекты, так что до скорого, не пропустите новую статью!
Как и обещал прилагаю архив с полным проектом этого примера: OpenGLTest_Cube.
Рисование сферы в OpenGL без использования gluSphere()?
10 ответов
При работе с glut я использовал glutsolidsphere для рисования своих сфер, но, перейдя на glfw, мне пришлось использовать glusphere. Я в основном скопировал всю функцию glutsolidsphere в свой собственный код, но получаю странную проблему освещения, где раньше меня не было. Вот код для сферы : void.
Как только у вас будет достаточное количество точек, вы нормализуете их векторы так, чтобы все они находились на постоянном расстоянии от центра твердого тела. Это приводит к тому, что стороны выпячиваются в форму, напоминающую сферу, с возрастающей гладкостью по мере увеличения количества точек.
Нормализация здесь означает перемещение точки таким образом, чтобы ее угол по отношению к другой точке был одинаковым, но расстояние между ними различалось. Вот вам двумерный пример.
A и B находятся на расстоянии 6 единиц друг от друга. Но предположим, что мы хотим найти точку на линии AB, которая находится на расстоянии 12 единиц от точки A.
Мы можем сказать, что C-это нормализованная форма B относительно A, с расстоянием 12. Мы можем получить C с помощью такого кода:
Если мы проведем этот процесс нормализации на множестве точек, все относительно одной и той же точки А и с одинаковым расстоянием R, то все нормализованные точки будут лежать на дуге окружности с центром а и радиусом R.
Здесь черные точки начинаются на линии и превращаются в дугу.
Этот процесс может быть расширен до трех измерений, и в этом случае вы получите сферу, а не круг. Просто добавьте компонент dz в функцию нормализации.

Если вы посмотрите на сферу в Epcot, вы можете как бы увидеть эту технику в действии. это додекаэдр с выпуклыми гранями, чтобы он выглядел более круглым.
Далее я объясню популярный способ генерации сферы с использованием широты и долготы (другой способ, икосферы, был уже объяснен в самом популярном ответе на момент написания этой книги.)
Сфера может быть выражена следующим параметрическим уравнением:
Генерация сферы затем включает в себя оценку параметрической функции через фиксированные интервалы.
Например, чтобы сгенерировать 16 линий долготы, вдоль оси u будет располагаться be 17 линии сетки с шагом π/8 (2π/16) (17-я строка оборачивается).
Следующий псевдокод создает треугольную сетку путем вычисления параметрической функции через равные промежутки времени (это работает для любой параметрической функции поверхности, а не только для сфер).
Код в этом примере быстро объясняется. Вы должны заглянуть в функцию void drawSphere(double r, int lats, int longs) :
Я экспериментировал с OpenGL, пытаясь нарисовать сферы внутри и снаружи прямоугольных призм. Проблема в том, что независимо от того, где я выбираю рисовать сферы, сетка всегда лежит поверх моих кругов, как видно ниже: То, что я делаю прямо сейчас, в основном использует glTranslatef для.
Если бы вы хотели быть хитрым, Как лиса, вы могли бы на полдюйма сдвинуть код с GLU. Проверьте исходный код MesaGL (http://cgit.freedesktop.org/mesa/mesa/).
Смотрите Красную книгу OpenGL: http://www.glprogramming.com/red/chapter02.html#name8 она решает проблему путем разбиения на полигоны.
Я знаю, что это немного не по теме, но я думаю, что это может помочь, если кто-то будет здесь искать этот конкретный случай.
Мой пример, как использовать ‘triangle strip’ для рисования сферы «polar», состоит в рисовании точек попарно:
Первая введенная точка (glVertex3f) соответствует параметрическому уравнению, а вторая смещена на один шаг Альфа-угла (от следующей параллели).
Один из способов состоит в том, чтобы сделать четырехугольник, обращенный к камере, и написать вершину и фрагмент shader, который визуализирует нечто, похожее на сферу. Вы можете использовать уравнения для круга / сферы, которые вы можете найти в интернете.
Одна приятная вещь заключается в том, что силуэт сферы выглядит одинаково с любого угла. Однако если сфера не находится в центре перспективного вида, то она, возможно, больше похожа на эллипс. Вы можете разработать уравнения для этого и поместить их в затенение фрагмента. Затем световое затенение должно изменяться по мере движения игрока, если у вас действительно есть игрок, движущийся в пространстве 3D вокруг сферы.
Может ли кто-нибудь прокомментировать, пробовали ли они это или это было бы слишком дорого, чтобы быть практичным?
Python адаптация ответа @Constantinius:
Похожие вопросы:
В основном я хочу вращающуюся землю 3d. Функция gluSphere не найдена. он доступен на iphone-х opengl-х годах? как я могу сделать сферу иначе?
Я использую OpenGL с C++ (но без шейдеров и GLSL) и рисую сферы (бильярдный шар) и цилиндры (Кий), используя функции библиотеки glu для их рисования. Я использую glBindTexture() для привязки.
У меня есть код для комнаты, предоставленной мне, мне нужно добавить сферу в комнате. Это выглядит так: PushMatrix(); //draw floor,walls,ceilings PushMatrix(); //draw some boxes on front wall.
При работе с glut я использовал glutsolidsphere для рисования своих сфер, но, перейдя на glfw, мне пришлось использовать glusphere. Я в основном скопировал всю функцию glutsolidsphere в свой.
Я экспериментировал с OpenGL, пытаясь нарисовать сферы внутри и снаружи прямоугольных призм. Проблема в том, что независимо от того, где я выбираю рисовать сферы, сетка всегда лежит поверх моих.
Мне нравится рисовать сферы в среде OpenGL, используя gluSphere(). Однако я хотел бы нарисовать границу вокруг сферы, причем граница представляет собой круг, идеально выровненный с рамкой камеры.
Я пытаюсь визуализировать сферу без использования функции gluSphere(). Но этот код не рендеринг какой-либо сферы. Я не могу точно определить, в чем заключается ошибка. import sys import math from.
Я пытаюсь нарисовать сферу в Matlab без использования функции сферы. Это мой код: r = 2; [ x,y ] = meshgrid(-4:0.1:4); z = sqrt(r^2-x.^2-y.^2); mesh(real(z)); hold on mesh(real(-z)); Приведенный.