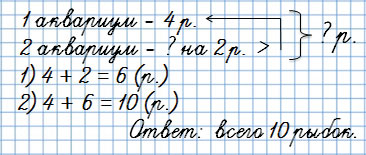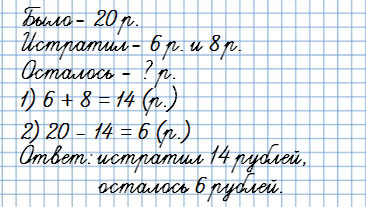Как сделать схему по математике
Памятка «Как начертить схему к задаче»
статья по математике (2 класс)
Памятка «Как начертить схематический чертёж к задаче».
Основные типы задач для второго класса и схемы к ним.
Скачать:
Предварительный просмотр:
Основные типы задач для второго класса и схемы к ним.
Задачи на нахождение суммы.
У Кати было 4 синих карандаша и 3 коричневых. Сколько всего карандашей у Кати?
Ответ: всего 7 карандашей.
За дачи на нахождение неизвестного слагаемого (обратные задачи)
У Кати было 7 карандашей, из них 4 синих карандаша, остальные коричневые. Сколько коричневых карандашей у Кати?
Чтобы найти неизвестную часть, надо из целого вычесть известную часть.
Ответ: 3 коричневых карандаша.
У Кати было 7 карандашей, из них 3 коричневых карандаша, остальные синие. Сколько синих карандашей у Кати?
Чтобы найти неизвестную часть, надо из целого вычесть известную часть.
Ответ: 4 синих карандаша.
Задачи на нахождение остатка.
У Наташи было 10 рублей. Она купила ручку за 8 рублей. Сколько денег осталось у Наташи?
Ответ: осталось 2 рубля.
Задачи на увеличение числа на несколько единиц.
Хозяйка купила 3 кг яблок, а груш на 2 кг больше. Сколько груш купила хозяйка?
При составлении чертежа к этой задаче вес яблок и груш обозначаем своим отрезком. Показываем, что груш столько же, сколько и яблок, да еще 2.

Хозяйка купила 3 кг яблок, а груш на 2 кг больше. Сколько всего фруктов купила хозяйка?

Г.
Ответ: всего 8 кг фруктов.
Задачи на уменьшение числа на несколько единиц.
У Зины 9 шаров, а у Кати на 2 шара меньше. Сколько шаров у Кати?
В чертеже к этой задаче важно показать, что у Кати шаров столько же сколько у Зины, но без 2.
З.
Ответ: 7 шаров к Кати.
У Зины 9 шаров, а у Кати на 2 шара меньше. Сколько всего шаров у Кати и Зины?
Ответ: всего 16 шаров.
Задачи на разностное сравнение.
К задаче на разностное сравнение можно использовать либо первую, либо вторую схему.
В.
Ответ: на 3 тетради больше.
По теме: методические разработки, презентации и конспекты
Открытый урок на краевом семинаре «Введение федерального государственного стандарта в общеобразовательном учреждении».
Урок математики в 1 классе по УМК «Гармония» Цель: систематизировать знания о сложении двузначных чисел без перехода через разряд, продолжить подготовительную работу к решению задач.Задачи урока.
Детям и родителям поможет такая подсказка при выполнении домашнего задания.
Эта памятка поможет учащимся правильно составить схемы к задачам.
Памятка для детей при составлении схемы к задаче.
Конспект урока математики по теме «Построение схемы к задаче. Дополнение текста задачи» 2 класс ОС «Гармония».
При решении задач использую эти схемы к задачам с 1 класса.
Памятка «Как составлять схемы к задачам».
методическая разработка по математике (1 класс) на тему
Эта памятка поможет учащимся правильно составить схемы к задачам.
Скачать:
Предварительный просмотр:
№ 1 Задача на нахождение суммы.
Дикие гуси живут 80 лет, а собаки – 20 лет. Орёл живёт столько, сколько собака и гусь вместе взятые. Сколько лет живёт орёл?
гуси собака
№ 2 Задача на увеличение и уменьшение числа на несколько единиц.
Длина синего отрезка 2 см, а красного – на 6 см больше. Какова длина красного отрезка?
С. 6 см
Кр.
№ 3 Составные задачи на нахождение слагаемого и вычитаемого
В столовой испекли 4 противня пирожков с капустой и 3 – с мясом. После обеда остался 1 противень. Сколько противней с пирожками съели?
ост. съели
№ 4 Составные задачи на нахождение суммы
Гр.
Ар. 2 ор.
№ 5 Составные задачи на разностное сравнение
В букете 7 гвоздик. Из них 4 белые, а остальные – розовые. На сколько меньше розовых гвоздик, чем белых?
7 гв.
белые розовые
Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
Сколько грибов нашёл Володя?
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было. Стало. «
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было. Осталось. «
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали. Осталось. «
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Сколько рыбок в двух аквариумах?
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
Задачи с составлением рисунка по условию:
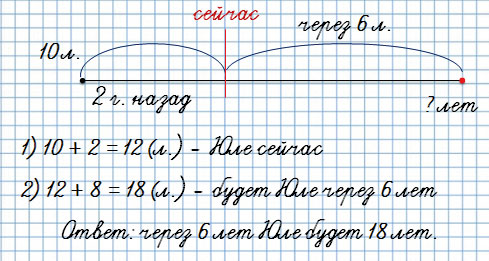
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Поделись с друзьями в социальных сетях:
Решение текстовых задач по математике с помощью унифицированных схем в начальных классах
Методику, которая здесь рассматривается, мы применяем на практике в течение 10 лет.
В процессе работы мы наблюдаем, что многим детям сложно усваивать учебную программу на стандартные “4” и “5”, то есть на те отметки, которые положительно принимают сами дети и их родители.
В своей работе мы стремимся к тому, чтобы у учеников не было страха перед “двойкой”, чтобы каждый ученик в своем темпе все-таки усваивал школьную программу. Поэтому для того, чтобы эти ребята могли учиться радостно, оптимистично, творчески; могли видеть результаты своего труда, при обучении решению задач мы используем схемы и придерживаемся четкого алгоритма в процессе обучения.
Основной особенностью данных схем является то, что ученик не составляет краткую запись к задаче, а находит готовую схему к своей задаче в таблице. Ребенок не находится в состоянии хаоса и растерянности, приступая решать задачу. У такого слабого ученика есть “опора под ногами”, ему есть на что опереться, есть с чего начать. Конечно, практика показывает, что не всем ученикам нужен такой план действий, есть ребята, которые могут подходить к решению задач творчески, многое анализировать в уме. Но на основании тех же практических наблюдений мы сделали вывод, что схемы не мешают сильным ребятам, не тормозят их развитие, а слабым ученикам они оказывают неоценимую помощь.
На первых порах кажется, что схемы замедляют темп обучения, что на уроке сделано мало. Но глубокие размышления над задачей окупаются сторицей. Мы считаем важным не количество решенных задач, а качество работы, проведенной над задачей. А это формирует очень ценные человеческие качества: честность, добросовестность, настойчивость.
Рассмотрим сначала сами схемы (Рисунок1). Это полная таблица, которой дети пользуются в 3-4 классах начальной школы и продолжают пользоваться в средних и старших классах, т. о. осуществляется преемственность между начальным и средним образованием. Для учащихся 1-2 классов мы используем часть полной таблицы (Рисунок2). Такие схемы каждый ребенок получает в начале учебного года, их желательно подписать: это приучает к аккуратности и ответственности за учебные принадлежности. Дети могут пользоваться одним печатным листом 2 года, что экономит время и затраты учителя. Для фронтальной работы у учителя на стенде висят схемы более крупного формата.
В таблице появились новые математические термины. Под словом “добавили” ребята подразумевают такие слова: нашли, посадили, приклеили и т. д. А бытовые слова: потеряли, выкорчевали, ушли, отцепили – ребята свободно заменяют математическим термином “убавили”.
Вопросительный знак в схеме лучше не ставить, вместо него целесообразнее рисовать над чертой красный “домик”, зеленый “домик”, потом внутри него можно записать, какое получилось число.
Чтобы глубже понять смысл задачи ученики в каждом действии обязательно пишут пояснения. Ответ тоже обязательно записывается полным предложением.
На первом этапе идет конкретно-образное обучение, а на остальных этапах – абстрактно-логическое. Детям особенно нравится первый этап, где все видно и можно потрогать.
Традиционно используется наименование для скорости: км/ч. Очень удобно и логично ввести такие же единицы измерения для цены и производительности: руб/кг, руб/м, руб/шт, дет/ч, га/дн, и т. д. Само наименование подсказывает детям, что это число будет записано в первой колонке.
При составлении сборника задач важно подбирать задачи с реальным жизненным сюжетом, придерживаться принципа целесообразности (не “зайчики на полянке”, а “ящики на складе у кладовщика”).
По заданной схеме ребята могут легко составить текст задачи сами, дома с родителями. Например, сочинить задачу к схеме Ж-3:
В феврале завод отправил 30 машин, разместив их на 5 платформах. В марте выпустили 54 машины. Сколько надо заказать платформ?
Этапы работы над задачами
Рассмотрим методику работы над текстовой задачей по унифицированным схемам на примере конкретной задачи (вариант работы: Приложение1).
Фронтальное знакомство с темой
Цель: дать общее представление о предстоящем зачете по теме.
Задачу читает учитель, и ребята знают, что она прозвучит 4 раза.
Ребятам для похода выдали деньги, чтобы они купили 3 кг яблок по 40 руб. Но яблок не оказалось, и ребята купили сливы по цене 24 руб/кг. Сколько килограммов слив они смогли купить?
После первого чтения ученики должны на черновике записать числовые данные с наименованиями и подумать, в какой колонке находится схема к данной задаче.
Методические пояснения: ребята вынуждены быть очень сосредоточенными, это труднее, чем читать текст самому.
Во время второго чтения задачи ребята чертят на черновике схему из колонки З-4 и расставляют в таблице известные данные.
После третьего чтения ученики уточняют, верно ли расставлены числа, записаны наименования и выясняют какой главный вопрос задачи – рисуют красный “домик” в нужной клетке и предполагают, сколько действий будет в решении задачи – отмечают это зелеными “домиками”.
Четвертый раз задача прозвучит позже, потому что сейчас ребята размышляют на черновиках самостоятельно. Учитель наблюдает за работой. Ребята работают в удобном для себя темпе.
Через 3-4 минуты весь класс начинает работать в тетрадях, а учитель – у доски. Сейчас появилась возможность выравнять сильных и слабых ребят, сверить ход решения задачи.
Так как дети будут давать ответы с места строго по заранее договоренной цепочке, то всем приходится быть очень внимательными, но страха перед неожиданным вызовом нет: есть возможность подготовить ответ заранее.
Учитель записывает на доске то, что предлагают ему дети. Ребята работают в тетрадях, а не на черновиках.
1 ученик: В таблице 3 колонки.
2 ученик: 1 колонка – цена.
3 ученик: Во второй колонке – количество.
4 ученик: 3 колонка – стоимость.
5 ученик: Первая строка – яблоки.
6 ученик: Вторая строка – сливы.
Учитель подводит и для себя, и для ребят маленькие итоги.
Учитель: Ребята, поднимите руки те, кто успел на черновике это сделать самостоятельно. Поставьте себе “плюсик” на полях в тетради.
7 ученик: Наименование в первой колонке – руб/кг.
8 ученик: Количество измеряется в килограммах.
9 ученик: Стоимость – в рублях.
10 ученик: 3 кг – это количество яблок, поэтому запишем во вторую колонку первой строки.
11 ученик: 40 руб/кг – это цена яблок, запишем в первую колонку первой строки.
Учитель: Цепочка закончилась. Молодцы, вы были очень внимательны, она ни разу не прервалась. Начинаем цепочку сначала.
1 ученик: 24 руб/кг – это цена слив, пишу в первую колонку, второй строки.
3 ученик: Мы должны узнать количество слив, поэтому красный “домик” будет во второй колонке второй строки.
4 ученик: Зеленых “домика” два.
Учитель: Поставьте себе “плюсики”, если у вас было так же.
Учитель: Чтобы узнать стоимость яблок, найдите в опорной таблице то правило, которое нам сейчас понадобиться.
При решении задач ребята должны использовать правила, как найти цену, скорость, количество и т. д. Эти правила выводились на конкретных ярких примерах с рисунками. Потом эти 9 правил были оформлены в виде опорной схемы (Рисунок7), и ребята не рассуждают, а должны просто вспомнить и автоматически применить правило (Чтобы найти время, надо работу разделить на производительность). Все 9 правил повторяются одновременно в едином блоке.
Учитель: Ребята первого варианта, расскажите это правило своему соседу по парте. (Чтобы найти стоимость, нужно цену умножить на количество.)
Кто доволен ответом товарища? Поднимите руку. Поставьте “плюсик”.
5 ученик: Первое действие – 40 умножить на 3.
6 ученик: 120 рублей.
7 ученик: Пояснение: стоимость яблок.
8 ученик: Запишем 120 в зеленый “домик”.
10 ученик: Теперь нужно найти стоимость слив.
Учитель: Подумайте, запишите свои мысли в черновике. Жду поднятые руки.
11 ученик: Про сливы нам известна цена, а количество неизвестно. Стоимость найти не можем.
Учитель: А кто же догадался? Поделитесь с товарищем своими мыслями. Кто считает, что сосед сказал правильно? Поднимите руку.
6 ученик: На сливы потратили те деньги, которые давали на яблоки, значит тоже 120 рублей.
Учитель: Молодец! Поставь себе три “плюсика”. У кого еще были такие мысли, тоже поставьте себе три “плюсика”.
Учитель: Начинаем третью цепочку. Вторая цепочка прервалась в двух местах.
1 ученик: Записываем 120 в зеленый “домик” – это стоимость слив.
Учитель: Ребята второго варианта, расскажите соседу по парте, какое правило сейчас нам понадобится. Можете посмотреть в опорные схемы. (Чтобы найти количество, нужно стоимость разделить на цену)
Учитель: Кому понравился ответ товарища? Поставьте “плюсик”.
2 ученик: 120 разделить на 24.
3 ученик: Получится 5 рублей.
4 ученик: Нет. 5 килограммов, а не рублей.
5 ученик: Пояснение – количество слив.
6 ученик: В красном “домике” запишем число 5
Учитель: Чтобы вы смогли записать ответ, я читаю задачу четвертый раз.
7 ученик: Вопрос: сколько килограммов слив смогли купить ребята?
8 ученик: Ответ: ребята смогли купили 5 кг слив.
Учитель: Кто заработал больше пяти “плюсиков”. Поднимите руки. Молодцы!
Учитель: Теперь поработаем над устной речью. Расскажите всю эту задачу как будто для своей мамы.
Итак, мы подробно рассмотрели фронтальное знакомство с задачей. Разберем методику остальных пунктов.
Совместное решение задач
Цель: формирование умений в решении задач.
Общее представление об алгоритме продолжаем нарабатывать совместно в черновиках и на доске. Чтобы уберечь ребят от бездумных шаблонов, вопрос в задаче меняется. Предлагаются задачи такого типа:
Для детского сада хотели закупить 8 маленьких мячей по цене 10 руб/шт. В продаже оказались только большие мячи, и их купили 5 штук. Сколько стоит большой мяч?
Ателье приобрело 20 метров тесьмы и 8 метров шнура. Сколько стоит вся покупка, если цена тесьмы 10 руб/м, а цена шнура на 4 рубля меньше?
Для столовой на 200 рублей купили яблоки и сливы. Яблоки продавались по 30 руб/кг, а сливы – по 40 руб/кг. Сколько купили яблок, если слив купили 2 кг?
На 360 рублей купили конфет и печенья. Конфет купили 4 кг по цене 40 руб/кг. Сколько рублей заплатили за все печенье?
Задача кажется знакомой и в тоже время над ней надо подумать. Универсальные схемы позволяют перебрать все возможные ситуации, в отличие от учебника, который такой возможности не дает. С помощью современной копировальной техники учитель может приготовить наборы задач для каждого ученика.
Самостоятельное решение задач
Это самый ценный этап обучения для развития личности.
Цель: выработка навыков в решении задач данных видов.
Проверочная перед зачетом
Цель: обобщить и уточнить знания учащихся по теме. Если есть пробелы в знаниях – устранить их.
А на этот этап отводится только один урок. Ученики работают самостоятельно на отдельных листочках. На этом уроке ученик еще имеет возможность получить 2 консультации у учителя. Такое правило только на первых порах кажется очень суровым, и многие ребята гордятся, что не воспользовались этим шансом. А сама возможность спросить поддерживает детей, подбадривает их.
Эта работа не оценивается, как и все предыдущие работы. Учитель внимательно изучает ошибки каждого ребенка.
Индивидуальные консультации
Цель: устранить обнаруженные пробелы в знаниях перед зачетом.
На занятиях продленной группы учитель каждому ребенку индивидуально указывает на его ошибки. Дает дополнительные задания. Перед зачетом ученик может еще подойти с вопросом. Внимание ребят в этот момент очень обострено, и учителю нужно спешить воспользоваться этим.
Зачет
Цель: проверка знаний и умений.
Раньше считалось, что зачеты – не для начальной школы. Они непонятны детям, пугают их. Считалось, что это работа для старшеклассников. Но практика показывает, что это не так. Зачетная система легко приживается в начальной школе и даже в первом классе. Мы часто слышим о своих учеников: “Ура, зачет!”. На зачетах дети чувствуют себя спокойнее и увереннее, чем на контрольных работах. Потому что контрольная работа – это неизвестность: дети не знают, какие именно будут задания, они могут только предполагать; а неизвестность всегда пугает. То, что будет на зачете всегда известно, причем известно с самого начала изучения темы. Дети знают, что на зачете будут только задачи и только такого вида, они готовятся к зачету целенаправленно. Зачет выполняется на отдельных листах и обязательно оценивается, оценка выставляется в журнал, даже если она неудовлетворительная. Потом ее надо обязательно исправить. Зачет удобен тем, что не только дети знают, чему они должны научиться, не только это четко себе представляет учитель, но и, что бывает очень редко при обычной системе обучения, знают родители: знают и поэтому могут помочь. (Приложение2, Приложение3)
Устранение пробелов
Цель: оказать каждому ребенку индивидуальную помощь для устранения пробелов в знаниях по этой теме.
Эта работа может занимать 1-6 дней. Помогают: учитель, родители, одноклассники, старшие ребята – выпускники. Целесообразно повторное решение знакомых задач. Эта работа приучает детей трудиться честно, добросовестно.
Повторный зачет
Цель: устранить пробелы и получить положительную оценку.
На таком уроке проводится дифференцированная работа. Сильные ребята могут углублять свои знания по математике, а слабые – сдают зачет. Они имеют право на одну подсказку учителя. Очень слабым ученикам можно дать знакомую задачу, чтобы они ее вспомнили.
Контрольная работа
Цель: проверить качество знаний через длительный промежуток времени.
Фронтального повторения накануне не делается, тема ребятам не сообщается заранее. Контрольная работа проводится обычно в конце четверти и включает в себя другие виды заданий по разным темам.
Таким образом, мы рассмотрели все 9 этапов работы по решению текстовых задач по унифицированным схемам на примере работы с задачами колонки З (стоимость).
Такая последовательность в работе над задачами дает возможность учителю дойти до каждого ученика, применяя в обучении личностно-ориентированный подход.
В заключении можно сделать вывод: не только у примера есть алгоритм решения, даже задачу можно разложить на четкие алгоритмические шаги. Вспоминая эти шаги и находя опоры в “Унифицированных схемах” слабый ученик может решить стандартную задачу.