Как сделать таблицу графика функции
Как построить график в Ворде
Приветствую, друзья! Сегодня я поделюсь с Вами информацией, как построить в Ворде график функции. В Интернете много примеров построения диаграмм с использованием Ворда и Экселя, но данные приемы не всегда могут соответствовать конечному результату.
Например, чтобы построить график функции по точкам, нужно заполнить таблицу данными, затем построить диаграмму типа График. Далее необходимо провести кучу дополнительных настроек, чтобы привести этот график к нужному виду.
И скажите, зачем столько трудностей, когда нужен всего-то рисунок этого графика для иллюстрации функции. Следовательно, проще взять и нарисовать этот график средствами векторного редактора, встроенного в Word.
Итак, давайте на примере параболы разберем, как построить в Ворде график этой функции. Если быть кратким, то сначала нарисуем график, а потом сохраним его как картинку и вставим в нужный документ. Я использую версию Word 2016, но все шаги вполне применимы и в более ранних версиях, так как отличия в интерфейсе минимальны.
Как построить в Ворде график функции по точкам
Создадим новый документ (Файл – Создать — Новый документ – Создать).
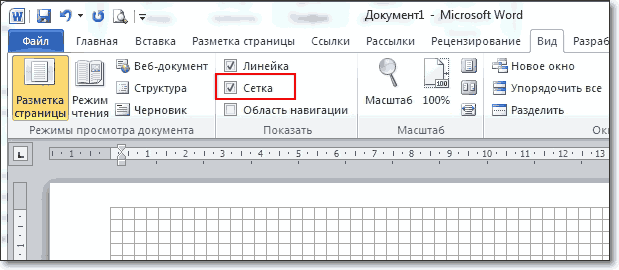
Для рисования графика по точкам, хорошо бы воспользоваться сеткой. Включаем её.
На вкладке Вид в разделе Показать ставим галочку напротив пункта Сетка. Теперь гораздо проще будет рисовать координатные оси и сам график.
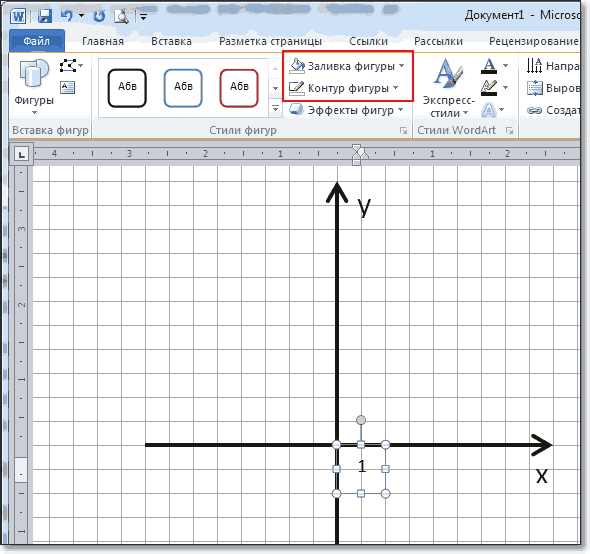
Рисуем оси координат
На вкладке Вставка в разделе Фигуры-Линии выбираем Стрелку. Курсор примет вид крестика. При нажатой левой кнопке мыши растягиваем стрелку до нужной длины.
При выделенной фигуре, на ее концах есть кружки. Потянув за любой из них, при нажатой левой кнопке мыши, можно изменить длину или направление стрелки.
Для рисования второй оси проделываем шаги, описанные выше.
Далее определяем на нашей сетке единичный отрезок и обозначаем его с помощью надписи (Вставка – Надпись – Нарисовать надпись). Растягиваем небольшой прямоугольник и вписываем в него цифру 1. Теперь убираем заливку и контур у надписи (фигура Надпись должна быть выделена). В ленте меню выбираем Средства рисования – Формат и в разделе Стили фигур выбираем для Заливки фигуры – Нет заливки, а для Контура фигуры – Нет контура. Теперь контур и заливка станут прозрачными.
Остается только перенести цифру поближе к нужному месту.
Если скопировать эту надпись и вставить несколько раз, то можно будет, заменив единичку, подписать оси координат, указать начало координат и расставить еще несколько значений на осях.
Ну, вот, координатная плоскость задана.
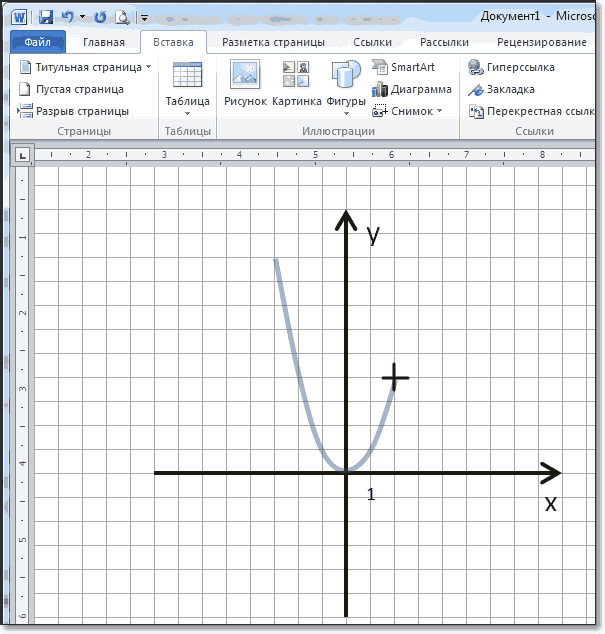
Рисуем график параболы у=х 2
В фигурах выбираем Кривая и на нашей координатной плоскости делаем одним кликом первую точку(-3,9), следующий клик в точке(-2,4), следующий в точке (-1,1) и так далее. На последней точке делаем двойной клик, чтобы завершить рисование кривой. Желательно постараться проставить все нужные точки графика за один проход.
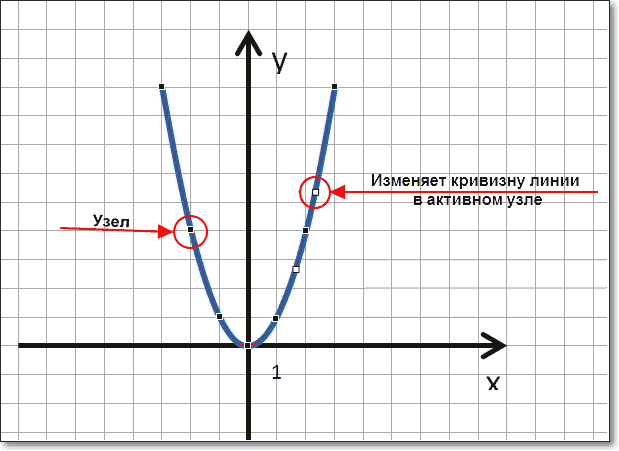
Но если не получилось, не беда, все можно поправить. Кликните на Вашу кривую правой кнопкой мыши и в контекстном меню вы берите пункт Начать изменение узлов.
Ваши узловые точки будут доступны для перемещения, можно скорректировать кривизну или длину кривой. Используя контекстное меню для кривой, узлы можно добавить или удалить.
Изменить цвет графика и его толщину можно в ленте меню Средства рисования – Формат и в разделе Стили фигур.
Помните! Режим сетки распространяется на все страницы документа. После его отключения, сетка на графике тоже исчезнет.
Совет! Делайте графики в отдельном документе, в целевой текст вставляйте скриншоты. Так у Вас будет возможность исправить неточности и поменять рисунок.
Теперь, когда график готов, нужно сделать его скриншот и вставить в нужный документ.
Как сделать скриншот в Ворде
Изменяем масштаб страницы так, чтобы рисунок графика занял максимальную область экрана. На клавиатуре нажимаем кнопку PrintScreen(PrtSc). Затем идем в нужный документ указываем место для вставки и даем команду Вставить из вкладки Главная на ленте инструментов или из контекстного меню. Вставится все содержимое экрана с ненужными нам частями.
Выполним обрезку. Кликаем по рисунку. На вкладке Работа с рисунками – Формат в разделе Размер выбираем инструмент Обрезка. Изменяем размер видимой области с помощью черных угловых маркеров и нажимаем кнопку Enter на клавиатуре для применения обрезки. Увеличить полученное изображение можно, потянув за угловые кружочки.
Теперь Вы знаете как построить в Ворде график. Этот способ я часто использую для рисования графиков или несложных рисунков в Ворде. Надеюсь, в Вашей копилке знаний он тоже не будет лишним. Вы можете поделиться с друзьями полученной информацией. Кнопочки социальных сетей ниже.
Построение графиков функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Чтобы ребенок разобрался в теории и чувствовал себя увереннее на школьных контрольных, запишите его на современные уроки математики в онлайн-школу Skysmart.
Интерактивные задания, математические комиксы и карта прогресса в личном кабинете — математика еще никогда не была таким увлекательным приключением!
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
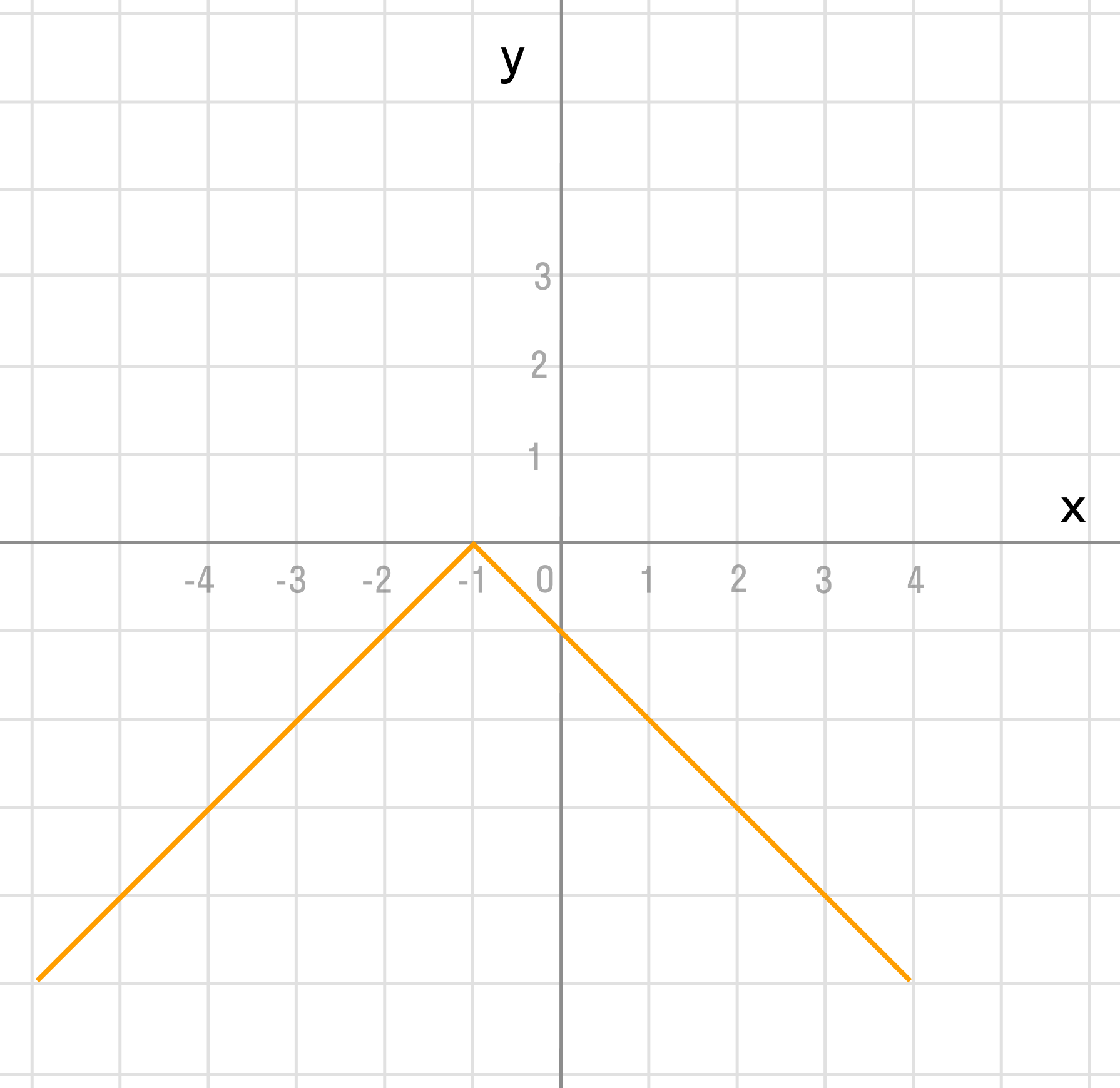
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.
Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.
Как построить график функции в Microsoft Excel
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графика линейной функции в Excel
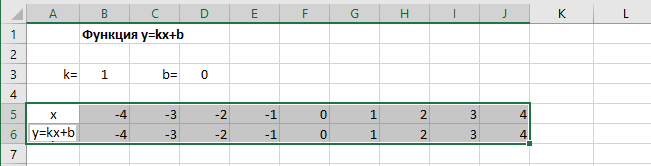
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
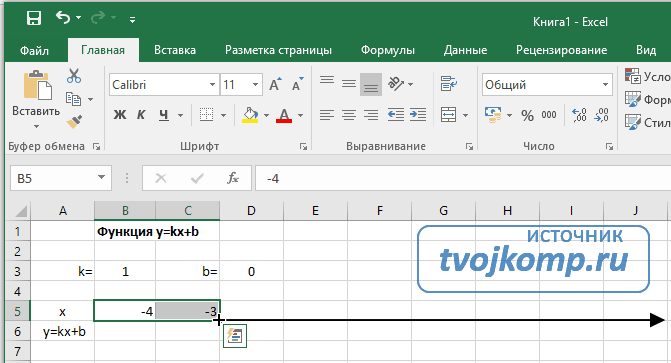
Далее строим таблицу значений линейной функции:
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
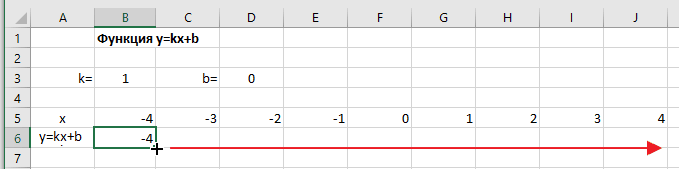
Построение графика функции
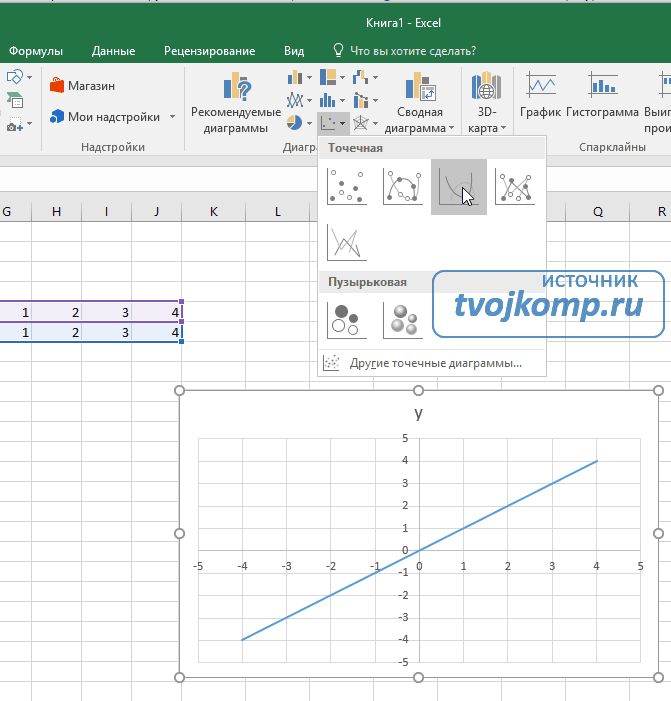
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
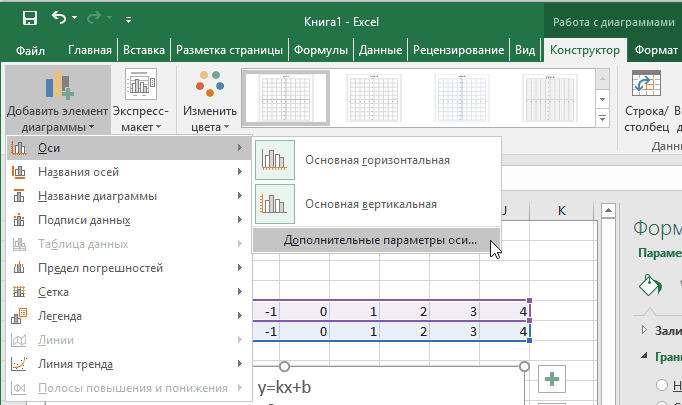
В правой части окна появиться боковая панель настроек Формат оси.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax 2 +bx+c
Выполните следующие действия:
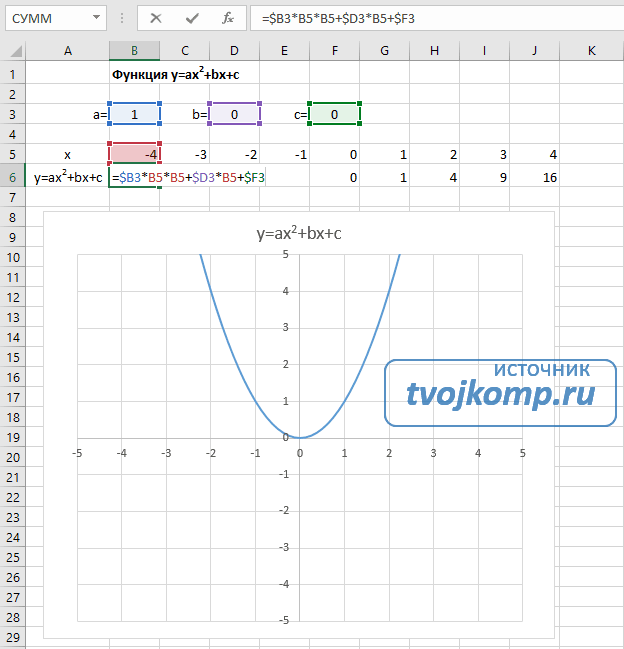
Кубическая парабола y=ax 3
Для построения выполните следующие действия:
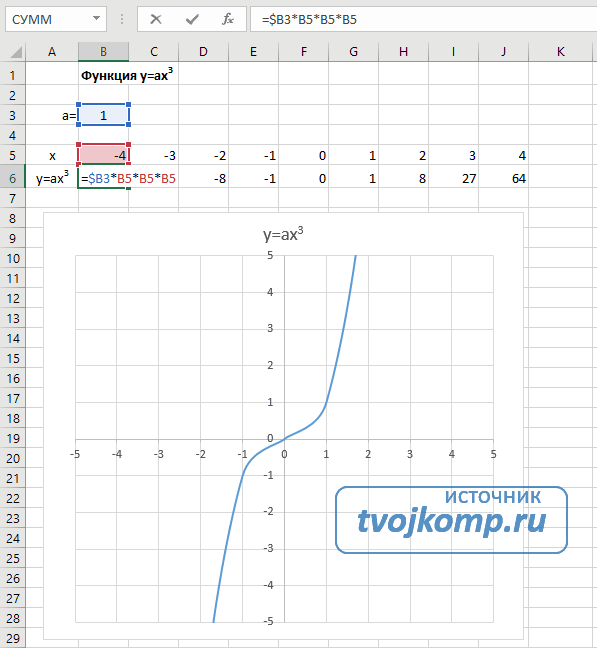
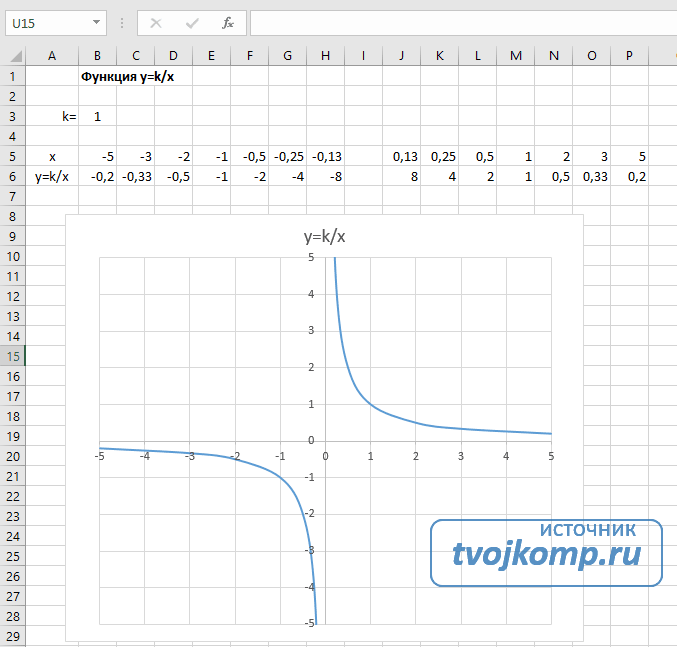
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
Построение тригонометрических функций sin(x) и cos(x)
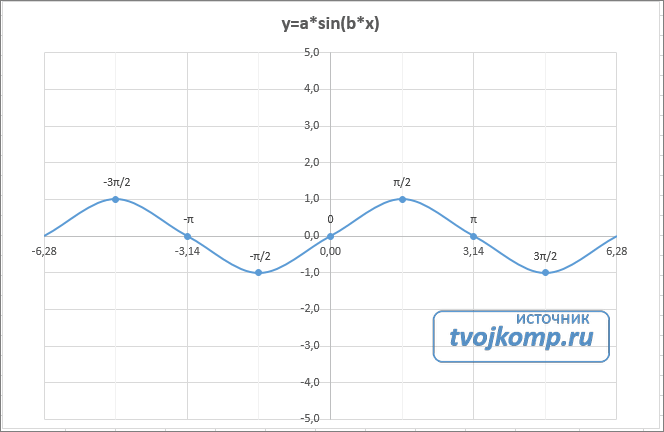
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
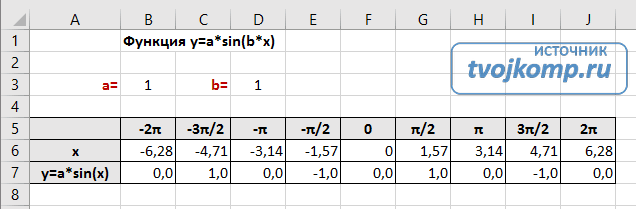
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
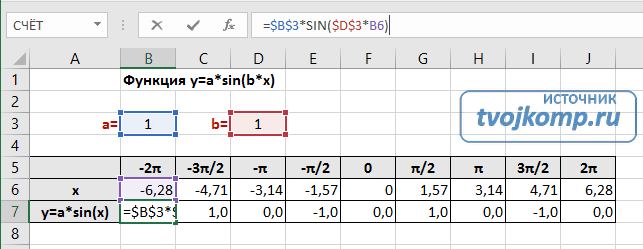
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
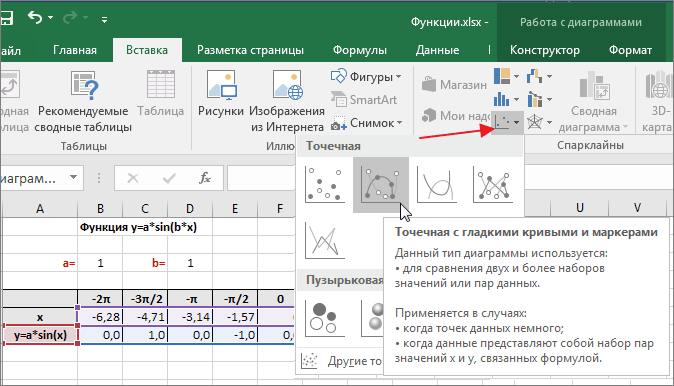
В итоге получим диаграмму.
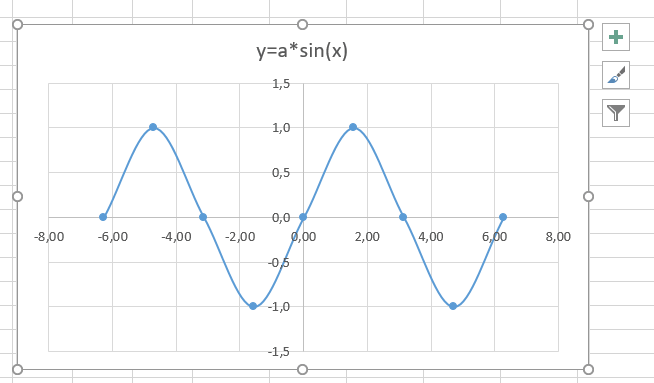
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
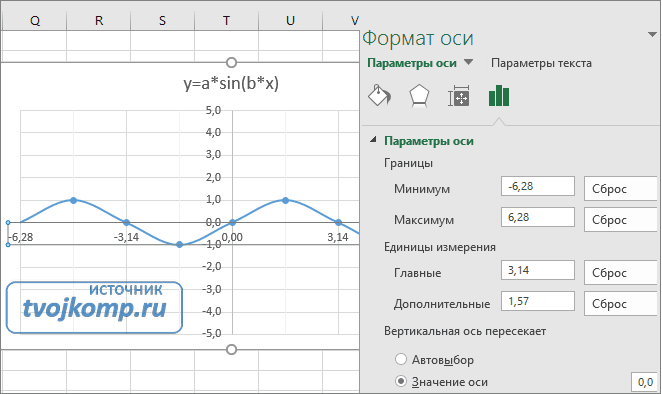
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
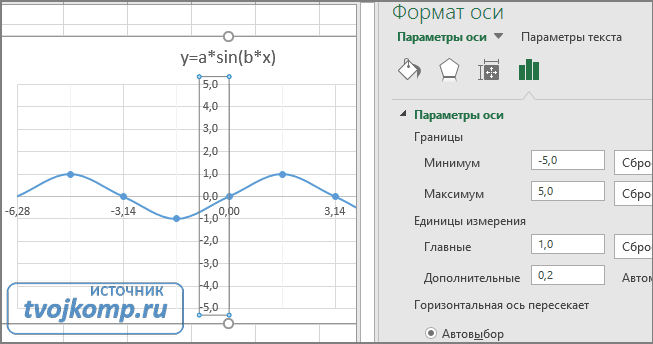
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
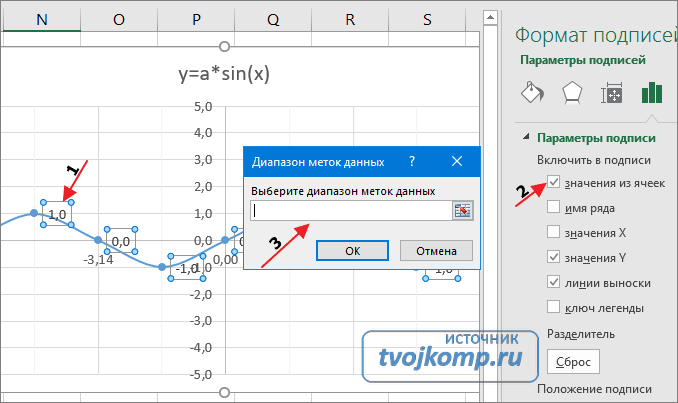
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
PS: Интересные факты про логотипы известных компаний
Дорогой читатель! Вы посмотрели статью до конца. Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.