Как сделать тессеракт своими руками
Учения о многомерных пространствах начали появляться в середине XIX века. Идею четырехмерного пространства у ученых позаимствовали фантасты. В своих произведениях они поведали миру об удивительных чудесах четвертого измерения.
Герои их произведений, используя свойства четырехмерного пространства, могли съесть содержимое яйца, не повредив скорлупы, выпить напиток, не вскрывая пробку бутылки. Похитители извлекали сокровища из сейфа через четвертое измерение. Хирурги выполняли операции над внутренними органами, не разрезая ткани тела пациента.
Каждая пара непараллельных трёхмерных граней пересекается, образуя двумерные грани (квадраты), и так далее. Окончательно, тессеракт обладает 8 трёхмерными гранями, 24 двумерными, 32 рёбрами и 16 вершинами.
Кстати согласно Оксфордскому словарю, слово tesseract было придумано и начало использоваться в 1888 Чарльзом Говардом Хинтоном (1853—1907) в его книге «Новая эра мысли». Позже некоторые люди назвали ту же самую фигуру тетракубом (греч. тетра — четыре) — четырёхмерным кубом.
Построение и описание
Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трёхмерного пространства.
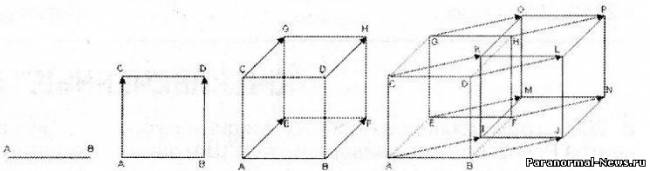
В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L. На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAGHFE. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.
Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб.
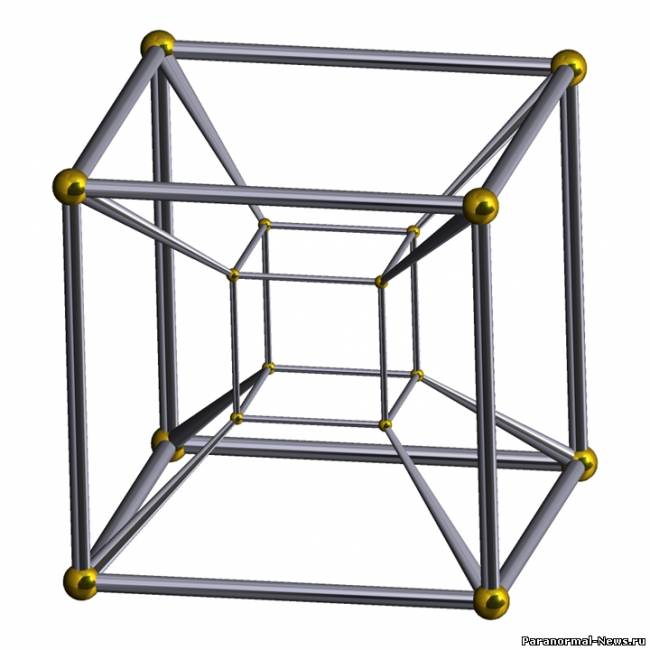
Возьмём проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями — боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» — трёхмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвёртой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.
Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Сам же четырёхмерный гиперкуб можно разбить на бесконечное количество кубов, подобно тому, как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.
Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру — развёртку. Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один — грань, ей противоположную. А трёхмерная развёртка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного — конечной «гиперграни».
Гиперкуб в искусстве
Тессеракт настолько интересная фигура, что неоднократно привлекал внимание писателей и кинематографистов.
Роберт Э. Хайнлайн несколько раз упоминал гиперкубы. В «Доме, который построил Тил», (1940) он описал дом, построенный как развёртка тессеракта, а затем вследствие землетрясения «сложившийся» в четвёртом измерении и ставший «реальным» тессерактом. В романе «Дорога славы» Хайнлайна описана гиперразмерная шкатулка, которая была изнутри больше, чем снаружи.
Рассказ Генри Каттнера «Все тенали бороговы» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
Сюжет фильма «Куб 2: Гиперкуб» сосредотачивается на восьми незнакомцах, пойманных в ловушку в «гиперкубе», или сети связанных кубов.
Математические абстракции вызвали к жизни представление о существовании параллельных миров. Под таковыми понимаются реальности, которые существуют одновременно с нашей, но независимо от неё. Параллельный мир может иметь различные размеры: от небольшой географической области до целой вселенной. В параллельном мире события происходят по-своему, он может отличаться от нашего мира, как в отдельных деталях, так и практически во всём. При этом физические законы параллельного мира не обязательно аналогичны законам нашей Вселенной.
На картине Сальвадора Дали «Распятие на кресте» изображен тессеракт. «Распятие или Гиперкубическое тело», — картина испанского художника Сальвадора Дали, написанная в 1954 году. Изображает распятого Иисуса Христа на развертке тессеракта. Картина хранится в Музее Метрополитен в Нью-Йорке
Всё началось в 1895 году, когда Герберт Уэллс рассказом «Дверь в стене» открыл для фантастики существование параллельных миров. В 1923 году Уэллс вернулся к идее параллельных миров и поместил в один из них утопическую страну, куда отправляются персонажи романа «Люди как боги».
Роман не остался незамеченным. В 1926 году появился рассказ Г. Дента «Император страны „Если»». В рассказе Дента впервые возникла идея о том, что могут существовать страны (миры), история которых могла пойти не так, как история реальных стран в нашем мире. И миры эти не менее реальны, чем наш.
В 1944 году Хорхе Луис Борхес опубликовал в своей книге «Вымышленные истории» рассказ «Сад расходящихся тропок». Здесь идея ветвления времени была, наконец, выражена с предельной ясностью.
Несмотря на появление перечисленных выше произведений, идея многомирия начала серьёзно развиваться в научной фантастике лишь в конце сороковых годов XX века, примерно тогда же, когда аналогичная идея возникла в физике.
Одним из пионеров нового направления в фантастике был Джон Биксби, предположивший в рассказе «Улица одностороннего движения» (1954), что между мирами можно двигаться лишь в одну сторону — отправившись из своего мира в параллельный, вы уже не вернетесь назад, но так и будете переходить из одного мира в следующий. Впрочем, возвращение в свой мир также не исключается — для этого необходимо, чтобы система миров была замкнута.
В романе Клиффорда Саймака «Кольцо вокруг Солнца» (1982) описаны многочисленные планеты Земля, существующие каждая в своём мире, но на одной и той же орбите, и отличаются эти миры и эти планеты друг от друга лишь незначительным (на микросекунду) сдвигом во времени. Многочисленные Земли, которые посещает герой романа, образуют единую систему миров.
В повести братьев Стругацких «Понедельник начинается в субботу» (1962) описаны путешествия персонажей в разные варианты описываемого фантастами будущего — в отличие от уже существовавших в фантастике путешествий в различные варианты прошлого.
Тессеракт и прочие гиперкубы.
Стукнула тут меня мысль нарисовать куб в десятом измерении. Ну точнее проекцию на двухмерный экран. Думал думал думал… Ну теперь когда придумал, все кажется таким простым, но тем не менее думал я напряжно. Да и тему сначала понять надо было.
В общем что такое куб в четвертом измерении.. Будем рассматривать через проекцию на третье.
Начнем с точки. Точка вытягивается в линию Это первое измерение. Линия расползается в квадрат, второе.
Квадрат раздваивается и расходится образуя куб.
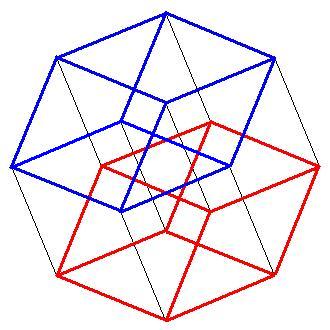
А далее таким же методом вытягиваем куб из куба, и соединяем соответствующие точки.
Вот пример каждая точка красного куба соединена с соответствующей точкой синего.
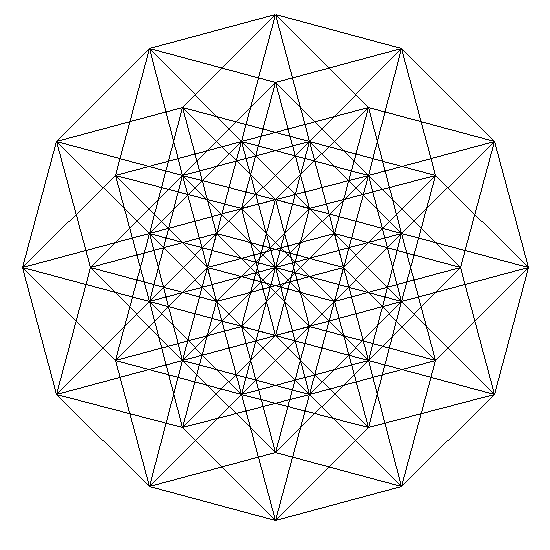
Тессеракт
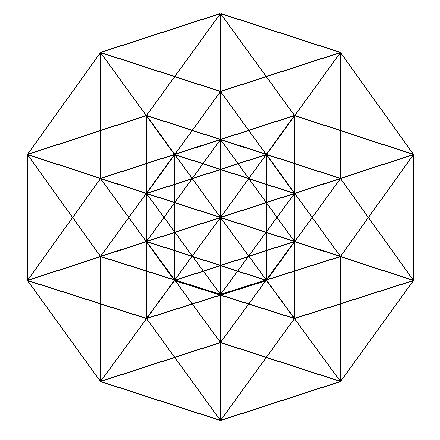
Далее идет пятое (тут я уже не стал возиться с обводкой)
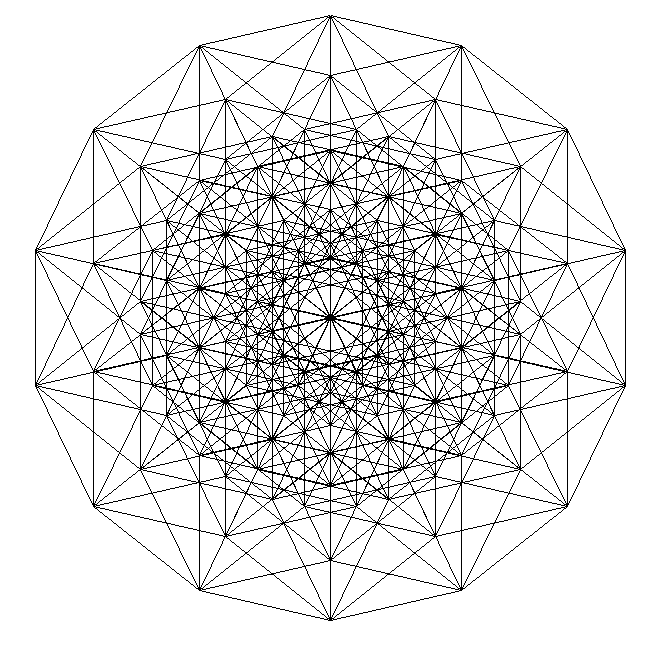
Пентеракт
Хексеракт
Хептеракт
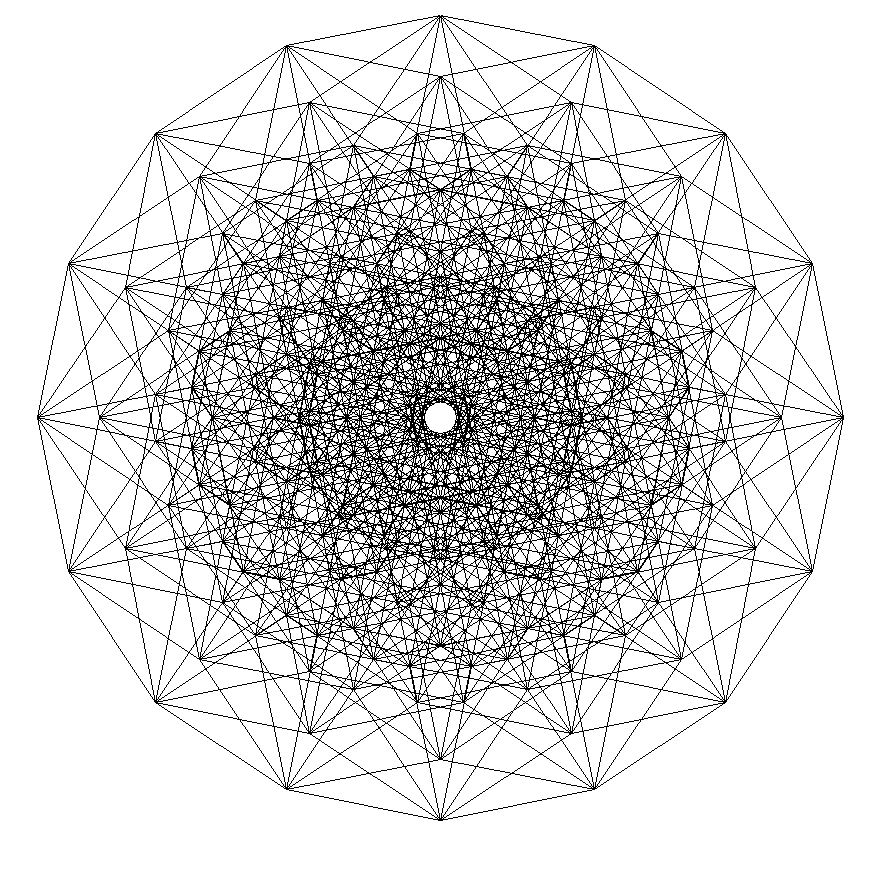
Октеракт
Энтенеракт
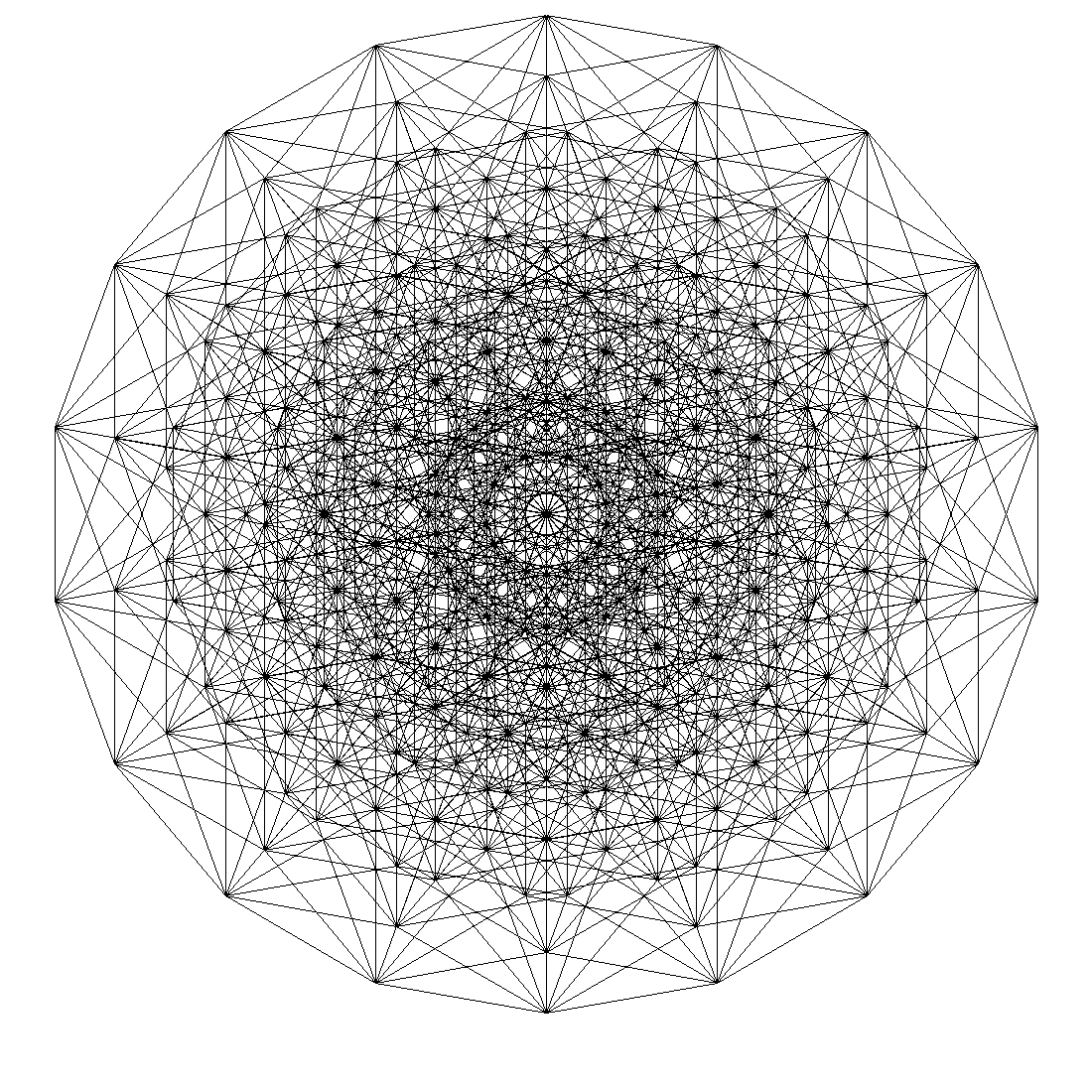
И десятимерный куб
Можно конечно и большие размерности и размеры (у меня тут файл 5000х5000 11мерный куб. вес правда всего 3 метра с небольшим) Но это уже если объявится желающий.
Да вот иногда я пишу подобную белеберду вместо кнопок бабло 🙂
54 thoughts on “ Тессеракт и прочие гиперкубы. ”
дружище ты бы к психологу сходил что ли 🙂
тесеракты какие то выдумываешь.
в пол седьмого утра точно бы не пошел, а вот попозжа может и прогулялся бы
Это ж надо было додуматься:) Хотя выглядит красиво, это да…
А на каком языке и с помощью каких библиотек реализовал это? Можно сделать скринсэйвер и выложить в паблик кстати.
На Делфи. рисовал стандартными процедурами на канве.
привет.
почты не нашел, а в аську по пустяку барабанить не хотеxtncz. Есть пару вопросов ричклику — судя по постам, ты с ними работаешь. Как у них с выплатами, задерживают как и сам бегун, или платят исправно как Зорька? Что нужно для аппрува, тупо дор какой-то общетематический в индексе показать, или что?
Заранее благодарен, пост можешь тереть, а ответить на почту, если не тяжело, ибо у тебя нет подписки)
Платят нормально.
Даты последних 8 платежей
20.10.2009
05.10.2009
17.09.2009
04.09.2009
19.08.2009
20.07.2009
25.06.2009
05.06.2009
Для апрува аккаунта надо показать свою вменяемость и адекватность.
Да, меня пример дора попросили показать. Спросили о трафике, о опыте, о том на каких форумах зареган и какова активность.
Уников на момент регистрации имел только 200 вместо 2к.
(Продублировал на почту)
Даже обычный гиперкуб 4-х мерный изобразить на плоскости невозможно, видел где-то в виде анимации, но все равно не то:) А то что вы изобразили это получается как бы тень от металлического каркаса таких фигур.
Я тоже видел анимацию.
Изобразить на плоскости объект большей мерности конечно невозможно. Не возможно изобразить даже обычный трехмерный куб. Поэтому изображение куба называется проекцией на плоскость.
о чем я и написал в посте словами «Ну точнее проекцию на двухмерный экран.»
Более того когда ты сказал «тень от металлического каркаса» ты сделал проекцию на трехмерность, то есть упростил гиперкуб в этот самый металлический каркас.
Так и я упростил всё до плоского изображения.
Хотя если совсем точно то тут изображенны проекции на плоскость трехмерных изображений, которые получены путем проекции гиперкубов в трехмерность.
Выложи программку что ли 🙂 с исходниками
Да какие исходники.. я программированию не обучен, поэтому думаю любого человека код введет в ступор.
На крайний случай я могу описать алгоритмы в отдельном посте. В конце концов именно в алгоритмах 90% сложности этой программы.
вот это офигеть. жги еще. на самом деле. вот у меня вопрос такой: ты можешь представить это все свое творчество в объеме? просто у меня например с этим всегда были траблы.. начиная с 4-го измерения, 3-х мерное пространство — 3 взаимно-перпендикулярных координатных оси, 4-х мерное пространство 4 оси. Куда ее пристроить-то? Ты я смотрю просто берешь и смещаешь трехмерный куб в разных направлениях, т.е каждая последующая мерность — реализуется виде некоторого движения. Это здорово, но все таки не то. В итоге получаешь просто траекторию движения точек куба, чем больше направлений смещения берешь,тем больше размерность. Однако, навряд ли это именно то, что происходит в действительности. Напиши, что думаешь по этому поводу.
Виноват. Вот перечитал пост свой. Все верно. Натупил слегка. Не о том подумал.
По факту это все проекции на третье измерение.
Думаю представить четвертое геометрическое пространство можно только абстрактно, но не визуально. Так как визуально все упирается в 2 и 3 мерность.
И даже если вспомнить разбитие на плоскости как это было в черчении, то трехмерный объект это просто три плоскости. А четырехмерный значит 4 объемности. (Смотря с каждой из четырех мерностей мы будем видеть трехмерный объект) формально четырехмерный объект будет описан, но чтобы представить его нужно иметь другой мозг.
И каждое новое смещение можно рассматривать как представление новой грани.. То есть мы копируем объект придавая ему еще одну глубину, будто бы мы посмотрели на объект с такого ракурса где видна новая ось. Но эти новые грани будут изначально трехмерными проекциями.
Если отойти от условностей и сделать многомерный куб в третьем измерении, то это будет тот же самые трехмерный куб, потому что для человеческого мозга не существует 4 геометрического измерения… Это как если бы человек из плоскости смотрел на куб, то он видел бы только квадрат.
Можно представить четвертое измерение как плоский срез пространства, имеющий глубину. Но это опять же проекция третьего измерения, где глубину третьего измерения подменяют глубиной четвертого.
Я вообще как то заморочился с перелинковкой сетки сателлитов в 400 штук такою штуку навоял парни долго потом всматривались в итоге сказали что надо лечиться,сейчас эта перелинковка цветет и процветает.
Извини за офтоп!!Но твои фигуры просто мне напомнили это!
Автор? ты что фентези перечитал? ил переиграл малость?
Отвечу на вопросы по очереди.
Автор
Перечитал
Переиграл
🙂
Мне думается что тесеракт- это просто невозможная фигура, как например треугольник из брусков у которого все углы по 90 градусов, просто интересная безделушка. А 4-ое измерение это из научной фантастики, одни лишь теории.
Да фигура невозможная, потому что человек не способен воспринимать 4 геометрическое измерение.
По повожу фантастики.
Когда программисты задают массив, они вполне могут сделать его четырех, пяти и более мерным.
Поэтому надо четко понимать о каком измерении идет речь. В широком смысле под четвертым измерением понимают время.
В узком геометрическом это просто дополнительная «глубина», которую человек не способен воспринять, и поэтому бОльшие мерности представляются проекциями на третье.
Поэтому, да. большие геометрические мерности существуют только теоретически.
«Это как если бы человек из плоскости смотрел на куб, то он видел бы только квадрат.»
А мне почему-то кажется, что если бы человек из плоскости смотрел на куб, то он видел бы его лишь как линию. Он мог бы понять, что это квадрат(не куб, заметьте, для двумерного человека понятие куб абстрактное, как для нас трёхмерных абстрактным является тессеракт) лишь в том случае, если бы ходил вокруг этого квадрата, изменение скорости удлиннения/укорачивания видимой линии служило бы показателем того, что там есть угол.
третье измерение глубина.
На плоскости мы будем видеть ширину и высоту, достаточно чтобы построить квадрат.
Если нарисовать на листе человечка и рядом квадрат, то конечно он его увидит как линию. Но как мы смотрим на плоскость (ведь изображение просто проецируется на сетчатке) и уже потом додумываем объем, так и он имея две оси вполне сможет понять, что перед ним квадрат.
И мне кажется обсуждение ушло куда то не туда.
Еще раз повторюсь это просто геометричекие проекции.
Я имею ввиду, что он живёт на плоскости, понятий «верх\низ» просто нет, как двумерный человек может посмотреть на плоскость сверху? Ведь «сверху» для него является третьим(гипотетическим) измерением. =))
если нет высоты то, тогда есть ширина и глубина. В любом случае есть два измерения а их достаточно для квадрата, на то она и плоскость.
Меня видимо поразило внезапное косноязычие, если я так долго не могу донести свою мысль… Представьте, что вы двумерный человек живущий на плоскости, посмотрите его глазами, как вы выберетесь в третье измерение(посмотрите сверху на плоскость, которая имеет длину и ширину)? Я прекрасно понимаю, что плоскости достаточно чтобы построить квадрат. А вот чтобы его увидеть нужно ещё одно измерение.
«…если бы человек из плоскости смотрел на куб, то он видел бы его лишь как линию. Он мог бы ПОНЯТЬ, что это квадрат», НО не смог бы увидеть.
Так же как и мы видим плоские объекты а не объемные. Но без всяких проблем рассуждаем о объеме.
И разве это
«Если нарисовать на листе человечка и рядом квадрат, то конечно он его увидит как линию. Но как мы смотрим на плоскость (ведь изображение просто проецируется на сетчатке) и уже потом додумываем объем, так и он имея две оси вполне сможет понять, что перед ним квадрат.» я не о том же самом говорил?
Поэтому я и говорил о высоте. он же своими глазами не только вперед-назад смотрит, но и вверх-вниз
тем не менее Penteract и Septeract существуют в виде матеиатических констант.
всё же, нарисовать 4х мерный объект в 3х мерном виде и поместить на 2х мерный экран, всё равно мы увидим не то, даже если предположить существование четвертого измрения
Вы всерьез думаете, что я не видел те картинки?
Мои картинки имеют равные грани, те — нет. Приглядитесь.
класс. молодец. а то народ совсем тупой
Уважаемый Elsper! (Извините, не знаю как правильно к Вам обратиться).
Я безмерно рада, увидев Ваши чертежи. Вы чертите ГОРИЗОНТАЛЬНЫЕ проекции трёхмерных проекций многомерных гиперкубов. И эти трёхмерные проекции многомерных гиперкубов (любых измерений!) можно чертить и во фронтальной, профильной проекциях, и в абсолютно в любых ракурсах. Более того, с помощью трубочек и лески я легко создала сами трёхмерные проекции четырёхмерного, пятимерного и шестимерного гиперкубов, на семимерный у меня не хватает трубочек.
Я написала работу «»Начала» геометрии многомерных измерений», в которой мною выявлен и подробно описан «Универсальный метод построения (черчения) трёхмерных проекций гиперкубов любых n-мерных измерений (3ПГК-n) в любых проекциях и ракурсах». Моя работа — это рукопись, правда, отсканированная, — потому что во время написания моих работ у меня не было компьютера, более того, я и сейчас, имея компьютер, не могу толком научиться чертить чертежи на компьютере — старая я, мне 64 года.
Уважаемый Elsper! Если Вам интересно прочитать или хотя бы просмотреть мою работу (где, кстати, я начертила горизонтальную проекцию трёхмерной проекции ДВЕНАДЦАТИМЕРНОГО гиперкуба), пожалуйста, сообщите мне свой электронный адрес, и я с радостью вышлю Вам свою работу.
С уважением,
Михайлова Людмила Михайловна.
Здравствуйте Людмила Михайловна.
Идея начертания гиперкубов была для меня просто тренировкой для мозгов. Я возвращался к ней еще два раза http://elsper.ru/stereokartinki-giperkuby-stereo-giperkuby/ и http://elsper.ru/2011/02/giperkuby-2/, но за три года уже почти утратил к ней интерес.
К тому же, так как я не рисовал их, а программировал, то мне тоже было нужно разработать универсальный метод построения, с чем я справился. И даже если бы не справился, то все равно думал бы сам, потому, что именно в этом и заключается смысл тренировки. В том, чтобы решить задачу самостоятельно.
Однако, если хотите, я могу сделать ссылку на вашу работу. Интересующиеся смогут ее скачать и прочитать.
Кроме того, вы упомянули трехмерные проекции. Если у вас есть фотографии, то их тоже можно опубликовать. Думаю они заинтересуют всех, кто сюда заходит.
Хотите так?
Здравствуйте, уважаемый Elsper!
Мне очень больно и стыдно признаваться в своей тупости: год назад я купила компьютер, научилась только пользоваться электронной почтой и выходить в интернет, я не могу писать на компьютере математические знаки, формулы, строить таблицы и чертить чертежи — старая я.
До 2011 года я жила в Туркмении. Там же написала свои работы по математике — карандашом, на бумаге, потом эти листы сканировались (т.е. хоть как-то приведены в электронный вид) — это всё, что я могла сделать там, в Туркмении.
С 2011 года я живу на Украине в г.Ивано-Франковске. В квартире я совершенно одна и мне совершенно некому помочь в освоении работы на компьютере.
Вот когда я пишу письмо в своей электронной почте, там на странице есть знак «Прикрепить файл», и я прикрепляю свои работы, — это мне показали. А как вот сейчас, в этом письме, прикрепить свою работу — я не знаю.
Я очень рада: рыская по интернету, я пока увидела — Вы единственный, кто вплотную смог приблизиться к построению горизонтальных проекций трёхмерных проекций n-мерных гиперкубов! Но Ваши проекции правильны только в тех случаях, где n-мерность НЕЧЁТНАЯ. Например, посмотрите на свой ОКТЕРАКТ (восьмое измерение) — в центре чертежа образовался «кружок пустоты», а в данной проекции октеракта центральная точка на чертеже совмещает 16 вершин.
Слава Богу, научили меня пользоваться скайпом. Вот по скайпу я могу показать Вам свои модели трёхмерных проекций четырёхмерного, пятимерного и шестимерного гиперкубов. Если Вы напишете на мою электронную почту свой электронный адрес, то я сообщу Вам свой «логин» для скайпа.
Конечно, я очень хотела бы, чтобы мои работы были хоть как-то опубликованы (для кого я их писала? — для людей!), но я не знаю как это сделать.
Спасибо, что ответили. Всего Вам самого доброго.
С уважением,
Михайлова Людмила Михайловна.
Программа начального многомерного геометрического моделирования NDL_4D
neoethics.narod.ru/n/neo_school/NDL_4D/index.html
Разработка возникла во многом благодаря и Вашей, Elsper, тематической компиляции, за что особое Вам большое спасибо. :)))
Возможно, в случае знакомства, возникнут мобильные конструктивы по дальнейшему развитию идеи освоения многомерных пространства — искренне будем благодарны за любые интересные мысли в данном направлении.
С уважением, Stellari.stA.G
Приятно, что мои работы служат не только мне. )
Правда сейчас меня интересуют совсем другие вопросы.