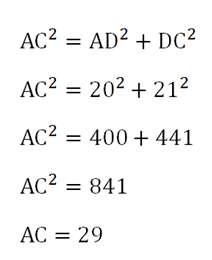Как сделать тетраэдр и параллелепипед

Геометрия

Тетраэдр и параллелепипед

План урока:

Тетраэдр

Пусть в пространстве есть точки М, Н, К, которые образуют ∆МНК и, таким образом, задают плоскость. Отметим в пространстве ещё одну точку Р, которая НЕ находится в плоскости МНК. Если мы соединим Р с вершинами ∆МНК, то получится объемная фигура. Её как раз именуют тетраэдром. Можно дать несколько различных определений тетраэдра, мы остановимся на следующем:

Такое название связано с тем, что в древнегреческом языке слово «тетра» означает «четыре». У тетраэдра ровно 4 грани и ровно 4 вершины. Приведем пример тетраэдра:

Легко увидеть, что гранями тетраэдра являются треугольники, в данном случае это ∆МРН, ∆МКР, ∆МНК и ∆РКН. Иногда одну из граней выделяют особенно и называют ее основанием тетраэдра. В этом случае три остальные грани именуют боковыми гранями тетраэдра.

Легко видеть, что есть всего 6 ребер тетраэдра. Действительно, назовем ∆МКН основанием тетраэдра. Оно, как и всякий треугольник, имеет 3 стороны. Ещё три ребра – это отрезки, соединяющие каждую из трех вершин ∆МКН с точкой Р. Перечислим грани, показанные на рисунке: МК, КН, МН, МР, НР и КР.

Заметим, что каждое ребро пересекается с четырьмя другими ребрами, и лишь с одним ребром скрещивается. Пары скрещивающихся ребер именуют противоположными ребрами. На рисунке противоположны друг другу грани РК и МН, МК и РН, МР и КН.

Тетраэдр называют простейшим многогранником. Действительно, у него всего 4 вершины, а меньшего количества вершин у многогранника быть не может (ведь любые три точки располагаются в одной плоскости). В этом тетраэдр во многом похож на треугольник – простейший из многоугольников. Как и треугольник, тетраэдр является очень жесткой конструкцией, поэтому его нередко используют в технике. Встречается тетраэдр и во многих научных дисциплинах, в том числе и в физике. Так, кристаллическая решетка алмаза, наиболее твердого материала на Земле, состоит из множества тетраэдров.

Наконец, отметим, есть особый, так называемый правильный тетраэдр. Его особенность заключается в том, что все его ребра имеют одинаковую длину.

Рассмотрим несколько задач.

Задание. Известно, что в тетраэдре АВСD:

Найдите длины ребер АВ, ВС и АС этого тетраэдра, а также площадь ∆АВС. Ответы округлите с точностью до целых.

Неизвестные стороны можно вычислить, применяя теорему косинусов для каждой грани тетраэдра. Запишем ее для ∆ADB:

Далее используем ∆ADC. Так как ∠ADC = 90°, то вместо теоремы косинусов можно записать ее частный случай – теорему Пифагора:

Задание. На ребрах АВ и АС тетраэдра ABCD отмечены их середины – точки M и N соответственно. Верно ли, что плоскость BCD и прямая MN параллельны?

Так как отрезок MN соединяет середины сторона АС и АВ, то он является средней линией в ∆АВС. Это значит, что NM||ВС. Получается, что в плоскости ВСD есть прямая, параллельная NM. Ранее мы изучали теорему, согласно которой из этого факта следует, что MN либо параллельна BCD, либо полностью находится в ней. Очевидно, что MN не располагается в BCD, ведь в противном случае в BCD полностью находились бы прямые АС и АВ (в том числе и точка А), а по определению тетраэдра А находиться в плоскости BCD не может. Значит, остается один вариант – NM и BCD параллельны.

Задание. Верно ли, что плоскость, проходящая через середины трех ребер тетраэдра, обязательно будет параллельна одной из граней тетраэдра?

Решение. Обозначим вершины тетраэдра буквами М, Н, К, Р. Пусть плоскость будет проходить по точкам N, T и L, которые являются серединами ребер MP, HP и КР соответственно:

Ясно, что плоскость NTL пересекает как минимум три грани: РМН, РНК и РКМ, то есть она может быть параллельна только грани МНК.

Заметим, что TL – это средняя линия в ∆НРК, а NT – средняя линия в ∆РМН. Поэтому TL||НК и NT||МН.

Получается, что в плоскостях NTL и МНК есть по две пересекающихся прямых, которые попарно параллельны. В NTL ими являются NTи TL, а в МНК– МН и НК. Напомним, что по признаку параллельности плоскостей этого факта как раз достаточно, чтобы NTL и МНК считались параллельными плоскостями. То есть утверждение, приведенное в условии задачи, верно.

Параллелепипед

Построим в плоскости параллелограмм АВСD. Далее через каждую его вершину проведем прямые, которые пересекут плоскость параллелограмма и при этом будут параллельны. Отложим на каждой такой прямой точки А₁, В₁, С₁ и D₁ так, чтобы все они находись по одну сторону от плоскости АВСD и выполнялось равенство:

Заметим, что в таком случае четырехугольники АА₁D₁D, АВВ₁А₁, ВСС₁В₁ и СDD₁C₁ будут параллелограммами, ведь у каждого из них две противоположные стороны одинаковы и параллельны. Также можно убедиться, что отрезки А₁D₁ и В₁С₁ тоже параллельны и одинаковы по свойству транзитивности:

Это значит, что и А₁D₁C₁B₁– параллелограмм. Получается, что мы смогли построить многогранник с 6 гранями, каждая из которых является параллелограммом. Такой многогранник именуется параллелепипедом.

Легко подсчитать, что у параллелепипеда ровно 8 вершин и 12 ребер. Если у граней параллелепипеда есть общее ребро, то их называют смежными гранями. В противном случае грани именуются противоположными. Также противоположными могут быть и вершины параллелепипеда, если они не находятся на одной грани. Так, в приведенном выше примере противоположны вершины А и С₁, В и D₁, C и А₁, D и B₁.

Существуют также и диагонали параллелепипеда. Это прямые, соединяющие его противоположные вершины:

Иногда в параллелепипеде выбирают две противоположные грани и называют их основаниями параллелепипеда. В таком случае остальные четыре грани именуются боковыми гранями.

Сформулируем важное свойство параллелепипеда.

Действительно, рассмотрим параллелепипед АВСDА₁В₁С₁D₁:

Сравним грани АВВ₁А₁ и CDD₁C₁. СD||АВ как стороны в параллелограмме АВСD, а DD₁||А₁A уже как стороны в параллелограмме АА₁D₁D. По признаку параллельности плоскостей выходит, что грани АВВ₁А₁ и CDD₁C₁ параллельны, ведь они содержат пересекающиеся прямые (СDи DD₁ в CDD₁C₁, АВ и АА₁ в АВВ₁А₁), которые друг другу попарно параллельны.

Теперь продемонстрируем, что эти грани ещё и равны. Отрезки АВ и СD одинаковы, так как входят в состав параллелограмма АВСD. По той же причине одинаковы и отрезки АА₁ и DD₁ (они находятся в другом параллелограмме, в АА₁D₁D). Также одинаковы ∠СDD₁ и ∠ВАА₁, так как у этих углов стороны являются сонаправленными лучами. Равенства двух сторон и находящегося между ними угла достаточно для доказательства равенства параллелограммов АВВ₁А₁ и CDD₁C₁, ч. т. д.

Второе важное свойство параллелепипеда связано с его диагоналями.

Теперь возьмем диагонали В₁D и, например, АС₁. Аналогично и для них можно доказать, что у них есть общая точка, делящая их пополам (для этого надо рассмотреть параллелограмм В₁С₁D₁A).Но мы уже знаем, что В₁D₁ делится пополам точкой О. Значит, именно она – общая для В₁Dи АС₁.

Наконец, рассмотрим также диагонали В₁D и ВD₁. И снова для них можно показать (используя параллелограмм BDD₁B₁), что они пересекаются в точке, делящей их пополам. И снова этой точкой будет О. Получается, что все четыре диагонали проходят через О, которая является для каждой из них серединой, ч. т. д.

Задание. Сумма длин всех ребер в параллелепипеде АВСDА₁В₁С₁D₁ составляет 120 см. Известно, что ВС больше АВ в 1,25 раза, а ВВ₁ больше ВС в 1,2 раза. Найдите длину каждого ребра данного параллелепипеда.

Заметим важный факт – хотя у параллелепипеда 12 ребер, их длины принимают всего три различных значения. Действительно, по свойству параллелограммов, являющихся его гранями, мы можем записать равенства:

Таким образом, сумма трех взаимно пересекающихся ребер (например, АВ, ВС и ВВ₁) будет ровно в 4 раза меньше суммы длин всех ребер:

Используя условие задачи, выразим длины ВС и ВВ₁ через АВ:

Задание. В параллелепипеде АВСDА₁В₁С₁D₁ отметили точки М, М₁, N и N₁, которые являются серединами АВ, А₁В₁, СD и С₁D₁ соответственно. Докажите, что многогранник МВNDM₁B₁N₁D₁– это также параллелепипед.

Заметим, что ребра АВ, СD, А₁В₁ и С₁D₁ одинаковы. Значит, одинаковы и их половины:

Отрезки ND и N₁D₁ лежат на параллельных ребрах СD и С₁D₁, значит, они сами параллельны. Если учесть, что они ещё и одинаковы, то получается, что DNN₁D₁ – параллелограмм. Аналогично МВ||DN, МВ||М₁В₁ и М₁В₁||N₁D₁, поэтому четырехугольники МВND, МВВ₁М₁ и М₁В₁N₁D₁– параллелограммы.Теперь нам осталось показать, что грани М₁D₁DМи В₁N₁NB– тоже параллелограммы.

Отметим, что ММ₁ = ВВ₁ (из параллелограмма МВВ₁М₁) и ВВ₁ = DD₁ (это параллельные грани параллелепипеда), поэтому отрезки ММ₁ и DD₁ одинаковы. Также они и параллельны, так как ММ₁||ВВ₁ и ВВ₁||DD₁. Это значит, что М₁D₁DМ – параллелограмм. Аналогично, сравнивая NN₁и ВВ₁ с отрезком DD₁, можно показать, что и В₁N₁NB– параллелограмм. В итоге получается, что у многогранника MBNDМ₁B₁N₁D₁ каждая из 6 граней – параллелограмм. То он по определению является параллелепипедом, ч. т. д.

Построение сечений

Любую объемную фигуру можно условно «разрезать» на две части, если провести через нее плоскость. Такая плоскость, проходящая через объемную фигуру, называется секущей плоскостью.

При пересечении плоскости и объемной фигуры образуется какая-нибудь плоская фигура, ее называют сечением. На рисунке выше сечение – это ∆NTL. Ещё раз отметим разницу между понятиями «секущая плоскость» и «сечение». Плоскость – это безграничная фигура, то есть она не имеет границ. Сечение же – это плоская фигура, имеющая границы.
Один из вопросов, который исследует стереометрия – это форма сечений тех или иных фигур.

Секущая плоскость пересекается с каждой гранью многогранника по отрезку, причем концы этих отрезков располагаются на ребрах многогранника. В результате сечение тетраэдра, параллелепипеда и вообще любого многогранника представляет собой плоский многоугольник. В тетраэдре всего 4 грани, поэтому его сечение не может иметь более 4 сторон. Другими словами, сечение тетраэдра – это либо четырехугольник, либо треугольник. У параллелепипеда уже шесть граней, а потому его сечения также могут быть даже шестиугольниками.

Важно уметь строить сечения, зная лишь несколько общих точек объемной фигуры и секущей плоскости. В случае многогранников достаточно просто найти все общие точки секущей плоскости и ребер, после чего их надо соединить отрезками. Заметим, что каждая сторона сечения должна находиться на одной из граней многогранника. Если с учетом этого ограничения построить сечение не получается, это значит, что сечение пересекает ещё какие-то ребра многогранника, и соответствующие точки пересечения надо найти. Рассмотрим несколько примеров задач на построение сечений.

Задание. Постройте сечение тетраэдра АВСD, проходящее через точки M, N и P:

Решение. Мы уже имеем три точки сечения. Однако просто соединить их нельзя, ведь точки M и P находятся на разных гранях. Значит, надо найти ещё одну общую точку сечения, находящуюся на каком-нибудь ребре.

Заметим, что плоскость MNP имеет с плоскостью BCD две общие точки – N и P. Значит, они пересекаются по прямой NP. Это значит, что если прямая ВС пересекается с NP, то эта точка пересечения будет принадлежать секущей плоскости. Продолжим ВС и NP, они пересекутся в некоторой точке Е, которая, как мы только что выяснили, находится на секущей плоскости:

Е находится на ВС, а ВС – это часть плоскости АВС. Значит, точка Е располагается на плоскости АВС. С другой стороны, и М находится на АВC. Получается, что у прямой ЕМ две точки принадлежат плоскости АВС, а потому она вся принадлежит АВС. Тогда мы можем найти ее точку пересечения с прямой АС, просто продлив прямую ЕМ:

Здесь мы обозначили точку пересечения ЕМ и АС буквой К. В итоге мы можем построить сечение MNPK, ведь каждая сторона этого многоугольника будет принадлежать одной из граней тетраэдра:

На картинке слева показано сечение MNPK. Именно это построение и необходимо выполнить, решая данную задачу. Справа для наглядности показан исходный тетраэдр, от которого секущая плоскость «отсекла» лишнее. Правую картинку строить при решении подобных задач не надо, она показана только для наглядности.

Заметим, что в этой задаче нам в качестве исходных данных были указаны три точки секущей плоскости, и этого хватило для построения сечения. Действительно, одна из аксиом стереометрии говорит, что три точки (если это не точки одной прямой) однозначно определяют плоскость, поэтому, зная только три точки, с помощью построений можно найти и все остальные точки.

Задание. В тетраэдре АВСD на грани АВD отмечена точка М. Постройте такое сечение тетраэдра, которое проходит через М и при этом параллельно грани АВС.

Решение. Секущая плоскость и плоскость АВС параллельны, при этом они пересекаются третьей плоскостью АВD. Тогда, по одной из изученных нами теорем, линии их пересечения с ABD будут параллельны. То есть чтобы построить отрезок, по которому секущая плоскость и грань ABD пересекаются, надо просто провести через M отрезок, параллельный ребру АВ:

Удалось получить две точки, Q и P, которые лежат на гранях. Теперь, чтобы найти линию пересечения секущей плоскости и грани АСD, надо провести через Р отрезок, параллельный АС. В итоге на грани CD мы получим ещё одну точку K:

Теперь у нас есть три точки сечения, при этом все отрезки, соединяющие их, лежат на гранях тетраэдра. Значит, мы уже можем построить сечение:

Обратите внимание, что отрезок QK также получился параллельным ребру СD, что говорит о правильности построения.

Задание. Постройте сечение параллелепипеда, проходящее через точки M, N и P, отмеченные на его гранях:

Решение. Здесь у задачи очень простое решение. Точки M, N, Р уже можно соединить так, что все соединяющие их отрезки будут находиться на гранях. Значит, никаких других точек искать не надо:

Задание. Решите предыдущую задачу, но при другом расположении точек М, N и Р:

Решение. Для начала мы можем построить отрезки MN и MР, по которым секущая плоскость пересекает грани АВВ₁А₁ и ВСС₁В₁:

Напомним, что противоположные грани у параллелепипеда параллельны. Поэтому и отрезки, которые образуются при их пересечении с секущей плоскостью, также должны быть параллельными. Значит, мы можем через N провести отрезок, параллельный MP, а через Р– отрезок, параллельный MN:

Теперь мы можем соединить KH (ведь K и H находятся на одной грани АВСD) и получить искомое сечение:

Задание. Решите предыдущую задачу при следующем расположении точек M, N и P:

Решение. На первом шаге мы можем построить отрезки MN и РМ. Секущая плоскость и плоскость АВВ₁А₁ пересекаются по прямой РМ. Найдем вспомогательную точку Е, в которой с РМ пересекается. Эта точка Е должна находиться в плоскости нижней грани АВСD, также она принадлежит секущей плоскости:

Так как верхняя и нижняя грани параллельны, то должны быть параллельны и линии их пересечения с секущей плоскостью. Но мы уже знаем, что секущая плоскость проходит через Е. Значит, линии пересечения секущей плоскости и нижней грани проходит через Е и параллельна MN. Этой информации достаточно для ее построения:

В результате нам удалось найти ещё две точки Q и F. Далее через F проводим отрезок, параллельный РМ:

В итоге мы получили 6 точек, которых достаточно для построения сечения:

Задание. В параллелепипеде АВСAА₁В₁С₁D₁ отрезок АС – это диагональ грани АВСD, а BD₁ – диагональ параллелепипеда. Постройте сечение, проходящее через АС и при этом параллельное диагонали BD₁.

Решение. Проведем на нижней грани диагональ BD. Она пересечется с АС в некоторой точке О:

Теперь мы можем в плоскости BDD₁ построить через точку О прямую, параллельную BD₁. Так как в этой же плоскости находится и DD₁, то DD₁ обязательно пересечется с этой прямой в какой-нибудь точке H:

Теперь проанализируем расположение плоскости АНСи диагонали BD₁. Так как BD₁||ОН, а ОН полностью принадлежит АНС, то получается, что BD₁||АНС. При этом АНС проходит через диагональ АС. Значит, АНС удовлетворяет условиям задачи и является искомым сечением:

В рамках сегодняшнего урока мы познакомились с простейшими объемными фигурами – тетраэдром и параллелепипедом. Также мы узнали о сечениях и способах их построения.

Источник