Как сделать тетрис на java
Тетрис на JavaScript
Отменяйте все дела, переносите встречи. Сегодня мы делаем тетрис, в который можно играть в браузере и на который можно потратить весь день.
В чём идея
Правила игры все знают: сверху в двумерный игровой стакан падают фигуры разной формы, составленные из модульных блоков. Внизу блоки соединяются. Если собрать целую горизонтальную линию из блоков, она исчезает, все остальные блоки сдвигаются на ряд ниже.
Наша задача — как можно дольше продержаться, чтобы экран не заполнился и было место, куда падать новым фигурам.
Если вдруг не знаете, как это работает, вот фрагмент с чемпионата мира по тетрису:
Код не мой
Код, который мы разбираем в этом проекте, написал американский разработчик Стивен Ламберт:
В этой статье мы объясним, как этот код работает.
Неожиданная сложность
Самое главное при программировании такой игры — это как-то хранить содержимое игрового экрана и учитывать движение фигур.
Если бы мы писали эту игру на Unreal Engine или Unity, первым интуитивным решением было бы сделать для блоков какую-то сущность типа объекта. У него были бы свойства — например, конфигурация. Может быть, мы бы захотели потом сделать взрывающиеся объекты или объекты с заморозкой, объекты с повышенной скоростью, отравленные объекты или что-то ещё в таком духе.
Но есть нюанс: смысл объекта в том, что он неделимый. А в «Тетрисе» все объекты запросто делятся, когда мы «закрываем линию». У какой-нибудь Т-образной фигуры может запросто пропасть хвостик, а у Z-образной фигуры — нижняя перекладина.
Получается, что фигура в тетрисе выглядит как объект, иногда ведёт себя как объект, но не обладает свойствами объекта. Поэтому объектный подход нам здесь не подходит.
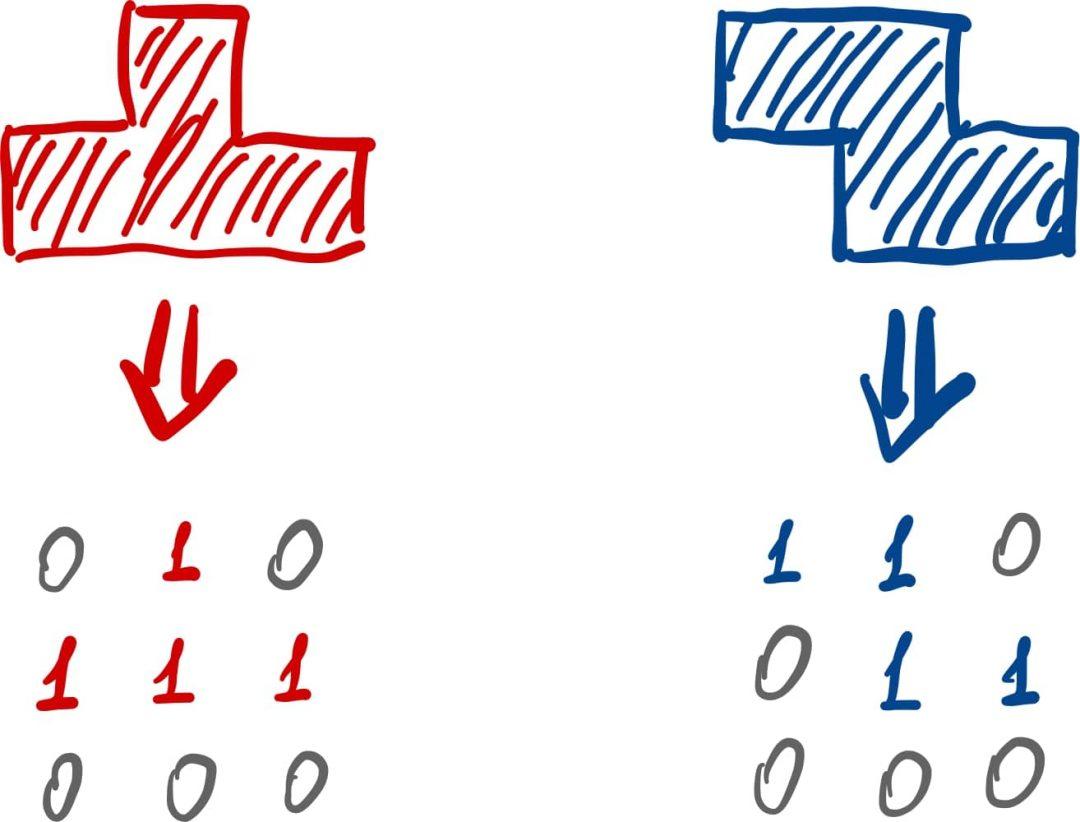
Решение — представить игровое поле в виде двумерного массива нулей и единиц. Ноль означает, что клетка свободна, а единица — что занята какой-то частью фигуры. Хранить и обрабатывать двумерный массив довольно просто, поэтому решение кажется логичным.
Сами фигуры тоже представим в виде двумерного массива из нолей и единиц, но особым образом — в виде квадрата, где единицы отвечают за части фигуры, а ноли — за пустое место:
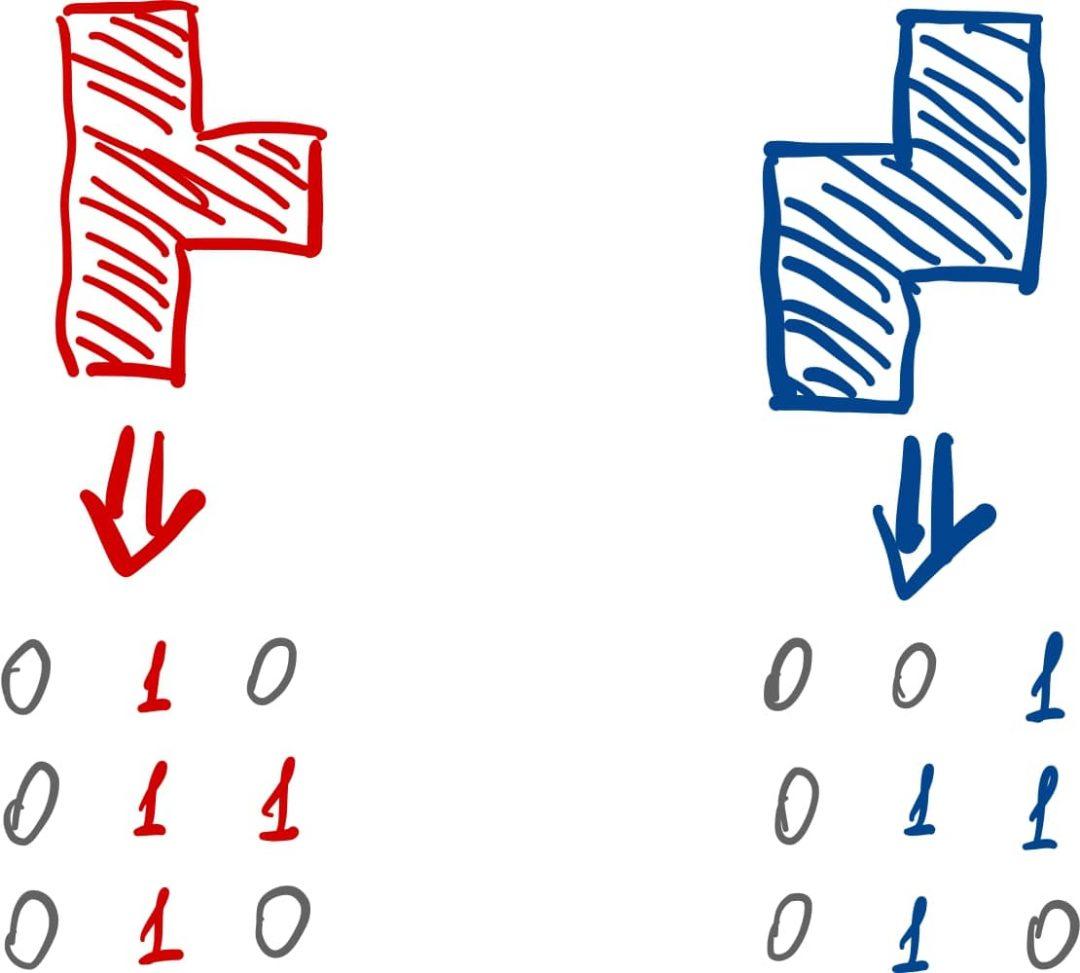
Если вместо квадрата просто взять фактические размеры фигуры и загнать их в массив, то при вращении они не влезут в исходный массив. А внутри квадрата их можно вращать как угодно — размер массива от этого не изменится:
Получается, что если мы добавим в общий массив с игровым цветом параметр, который отвечает за цвет, то можем рисовать каждую фигуру своим цветом. Так и сделаем.
Подготовка страницы
Игра будет работать на HTML-странице с помощью элемента Canvas — это холст, на котором мы можем рисовать произвольные фигуры через JavaScript.
Возьмём пустую страницу и сразу нарисуем на ней игровое поле. Сразу сделаем чёрный фон, игровое поле поставим по центру, а его рамки сделаем белыми:
Всё остальное сделаем скриптом. Добавим тэг сразу после того, как нарисовали холст, и начнём писать содержимое скрипта.
Заводим переменные и константы
Пока что всё просто:
Генерируем выпадающие фигуры
Первое, что нам понадобится для этого, — функция, которая выдаёт случайное число в заданном диапазоне. По этому числу мы будем выбирать фигуры.
Теперь мы можем создать последовательность из выпадающих фигур. Логика будет такая:
Последний этап в этом блоке — получить из игровой последовательности, которую мы только что сделали, следующую фигуру, которая у нас появится. Мы должны знать, что это за фигура; как она рисуется; откуда она начинает движение. Обратите внимание: на выходе мы получаем не только двумерный массив с фигурой, а ещё и название и её координаты. Название нам нужно для того, чтобы знать, каким цветом рисовать фигуру.
Движение, вращение и установка фигуры на место
В тетрисе мы можем вращать каждую фигуру на 90 градусов по часовой стрелке сколько угодно раз. А так как у нас фигура — это двумерный массив из чисел, то быстро найдём в интернете готовый код для поворота числовой матрицы:
После каждого поворота и при каждой смене позиции нам нужно проверить, а может ли в принципе фигура так двигаться? Если движению или вращению мешают стенки поля или другие фигуры, то нужно сообщить программе, что такое движение делать нельзя. Дальше мы будем делать эту проверку перед тем, как что-то отрисовывать на экране.
Если проверка не прошла, то мы не делаем последнее движение, и фигура просто продолжает падать вниз. Если ей некуда падать и она упёрлась в другие, то нам нужно зафиксировать это в игровом поле. Это значит, что мы записываем в массив, который отвечает за поле, нашу матрицу фигуры, пропуская ноли и записывая только единицы.
Как только фигура встала, нам нужно проверить, получился целый ряд или нет. Если получился — сдвигаем на один ряд вниз всё, что сверху. Такую проверку делаем каждый раз при установке фигуры и начинаем с нижнего ряда, поднимаясь наверх.
Что будет, когда мы проиграем
Когда фигура при окончательной установке вылезает за границы игрового поля, это значит, что мы проиграли. За это у нас отвечает флаг gameOver, и его задача — остановить анимацию игры.
Чтобы было понятно, что игра закончена, выведем надпись GAME OVER! прямо поверх игрового поля:
Обрабатываем нажатия на клавиши
Всё как в обычном тетрисе: стрелки влево и вправо двигают фигуру, стрелка вверх поворачивает её на 90 градусов, а стрелка вниз ускоряет падение.
Единственное, о чём нужно не забыть — после каждого нажатия вызвать проверку, можно ли так двигать фигуру или нет.
Запускаем движения и анимацию
Смысл главного цикла игры такой:
Так как кадры меняются быстро, мы не заметим постоянного очищения и отрисовки. Нам будет казаться, что фигура просто движется вниз и реагирует на наши действия.
Последнее, что нам осталось сделать, — запустить игру:
// старт игры rAF = requestAnimationFrame(loop);
Готовый результат можно посмотреть на странице с игрой.
Как написать свой Тетрис на Java за полчаса
В предыдущих статьях этой серии мы уже успели написать сапёра, змейку и десктопный клон игры 2048. Попробуем теперь написать свой Тетрис.
Нам, как обычно, понадобятся:
Прежде чем задавать вопрос в комментариях, не забудьте заглянуть в предыдущие статьи, возможно там на него уже давался ответ. Исходный код готового проекта традиционно можно найти на GitHub.
С чего начать?
Получение данных от пользователя
Код, честно говоря, достаточно капитанский:
Интерфейсы для клавиатурного и графического модулей
Так как многим не нравится, что я пишу эти модули на LWJGL, я решил в статье уделить время только интерфейсам этих классов. Каждый может написать их с помощью той GUI-библиотеки, которая ему нравится (или вообще сделать консольный вариант). Я же по старинке реализовал их на LWJGL, код можно посмотреть здесь в папках graphics/lwjglmodule и keyboard/lwjglmodule.
Интерфейсы же, после добавления в них всех упомянутых выше методов, будут выглядеть следующим образом:
Отлично, мы получили от пользователя данные. Что дальше?
А дальше мы должны эти данные обработать и что-то сделать с игровым полем. Если пользователь сказал сдвинуть фигуру куда-то, то передаём полю, что нужно сдвинуть фигуру в таком-то направлении. Если пользователь сказал, что нужно фигуру повернуть, поворачиваем, и так далее. Кроме этого нельзя забывать, что 1 раз в FRAMES_PER_MOVE (вы же открывали файл с константами?) итераций нам необходимо сдвигать падающую фигурку вниз.
Сюда же добавим проверку на переполнение поля (в Тетрисе игра завершается, когда фигурам некуда падать):
Так, а теперь мы напишем класс для того магического gameField, в который мы всё это передаём, да?
А инициализировать мы их будем так:
А вот теперь мы переходим к классу, который отвечает за хранение информации об игровом поле и её обновление.
Класс GameField
Этот класс должен, во-первых, хранить информацию о поле и о падающей фигуре, а во-вторых, содержать методы для их обновления, и получения о них информации – кроме тех, которые мы уже использовали, необходимо написать метод, возвращающий цвет ячейки по координатам, чтобы графический модуль мог отрисовать поле.
Хранить информацию о поле…
…и о падающей фигуре
TpReadableColor — простой enum, содержащий элементы с говорящими названиями (RED, ORANGE и т.п.) и метод, позволяющий получить случайным образом один из этих элементов. Ничего особенного в нём нет, код можно посмотреть тут.
Это все поля, которые нам понадобятся. Как известно, поля любят быть инициализированными.
Сделать это следует в конструкторе.
Конструктор и инициализация полей
А что это там за spawnNewFigure()? Почему инициализация фигуры вынесена в отдельный метод?
На этом с хранением данных мы закончили. Переходим к методам, которые отдают информацию о поле другим классам.
Методы, передающие информацию об игровом поле
Таких метода всего два. Первый возвращает цвет ячейки (для графического модуля):
А второй сообщает, переполнено ли поле (как это происходит, мы разобрали выше):
Методы, обновляющие фигуру и игровое поле
Сдвиг фигуры
Что мы сделали в этом методе? Мы запросили у фигуры ячейки, которые бы она заняла в случае сдвига. А затем для каждой из этих ячеек мы проверяем, не выходит ли она за пределы поля, и не находится ли по её координатам в сетке статичный блок. Если хоть одна ячейка фигуры выходит за пределы или пытается встать на место блока – сдвига не происходит. Coord здесь – класс-оболочка с двумя публичными числовыми полями (x и y координаты).
Поворот фигуры
Логика аналогична сдвигу:
Падение фигуры
Сначала код в точности повторяет предыдущие два метода:
Так как в результате переноса ячеек какая-то линия может заполниться полностью, после каждого добавления ячейки мы проверяем линию, в которую мы её добавили, на полноту:
Этот метод возвращает истину, если линию удалось уничтожить. После добавления всех кирпичиков фигуры в сетку (и удаления всех заполненных линий), мы, при необходимости, запускаем метод, который сдвигает на место пустых линий непустые:
Теперь GameField реализован почти полностью — за исключением геттера для фигуры. Её ведь графическому модулю тоже придётся отрисовывать:
Теперь нам нужно написать алгоритмы, по которым фигура определяет свои координаты в разных состояниях. Да и вообще весь класс фигуры.
Класс фигуры
Реализовать это всё я предлагаю следующим образом – хранить для фигуры (1) «мнимую» координату, такую, что все реальные блоки находятся ниже и правее неё, (2) состояние поворота (их всего 4, после 4-х поворотов фигура всегда возвращается в начальное положение) и (3) маску, которая по первым двум параметрам будет определять положение реальных блоков:
Rotation мод здесь будет выглядеть таким образом:
Соответственно, от самого класса Figure нам нужен только конструктор, инициализирующий поля:
И методы, которыми мы пользовались в GameField следующего вида:
Вдобавок, у фигуры должен быть цвет, чтобы графический модуль мог её отобразить. В тетрисе каждой фигуре соответствует свой цвет, поэтому цвет мы будем запрашивать у формы:
Форма фигуры и маски координат
Чтобы не занимать лишнее место, здесь я приведу реализацию только для двух форм: I-образной и J-образной. Код для остальных фигур принципиально не отличается и выложен на GitHub.
Храним для каждой фигуры маску координат (которая определяет, насколько каждый реальный блок должен отстоять от «мнимой» координаты фигуры) и цвет:
Реализуем методы, которые использовали выше:
Ну а сами маски координат я предлагаю просто захардкодить следующим образом:
Т.е. для каждого объекта enum‘а мы передаём с помощью импровизированных (других в Java нет) делегатов метод, в котором в зависимости от переданного состояния поворота возвращаем разные реальные координаты блоков. В общем-то, можно обойтись и без делегатов, если хранить в каждом элементе отсупы для каждого из режимов поворота.
Свой тетрис на JavaScript: прокачиваем проект
Как-то раз мы писали собственный тетрис на JavaScript. Мы закончили на том, что у нас есть простое игровое поле, фигуры и базовая логика игры. Ещё игра умеет останавливаться, когда для фигур больше нет места. Но этого недостаточно, чтобы считаться полноценной игрой.
Чтобы это исправить, вот что мы добавим сегодня в игру:
Всё это несложно, но требует внимания. Чтобы доработать игру, будем использовать код из первой части проекта:
Отображаем текущий уровень и набранные очки
Если мы сделаем вывод информации об уровнях и статистике внутри игрового стакана, это будет неудобно: текст будет наползать на фигуры и мешать игре. Значит, нам нужно добавить отдельный блок, где мы будем писать все игровые данные. Сделаем его сразу после объявления поля для игры и даём блоку имя score:
Так как у нас в глобальных стилях прописана рамка для холста, а для отображения статистики рамка не нужна, поставим ей нулевую толщину.
Заметьте: теперь у нас на странице есть два объекта типа canvas — то есть два холста. В одном рисуется игра, в другом выводятся очки. Теперь мы сможем обращаться к этим холстам отдельно и рисовать в каждом то, что нам нужно, независимо друг от друга.
Вот как получить доступ к новому холсту:
// получаем доступ к холсту с игровой статистикой
const canvasScore = document.getElementById(‘score’);
const contextScore = canvasScore.getContext(‘2d’);
Добавим в скрипт новые переменные — они нам сразу пригодятся на следующем этапе:
Теперь выведем на экран всю игровую статистику. Для этого перед главным циклом игры сделаем новую функцию showScore():
Цифры вроде 15, 20, 50, 160 — это координаты по вертикали и горизонтали, где должны находиться наши текстовые блоки. Без этих координат они все налезут друг на друга.
Последнее, что нам осталось сделать — вызвать эту функцию внутри основной функции loop() командой showScore().
Спрашиваем имя игрока
Чтобы знать, кому принадлежит рекорд игры, будем спрашивать имя при каждом запуске игры:
name = prompt(«Ваше имя», «»);
Этот код мы напишем сразу после объявления всех переменных, чтобы он выполнился на старте один раз. Сменить имя в процессе игры будет нельзя, но это и не нужно.
Считаем очки
Считать будем так: за каждую собранную линию начисляем 10 очков, по количеству кубиков в ней. В оригинальном тетрисе считается немного иначе, но для простоты сделаем так.
Для подсчёта очков находим в функции placeTetromino() проверку, заполнен ли ряд целиком, и сразу первым действием в этой проверке пишем:
Заметьте: нам не нужно городить новую сложную функцию по определению заполняемости строк — мы ее уже написали, когда программировали основную логику игры. Нужно просто дополнить уже существующую рабочую функцию одним новым действием — начислением очков. Если бы мы хотели добавить звуков или спецэффектов, мы бы точно так же добавили в эту функцию новые команды.
Теперь добавим проверку рекорда — побили мы его уже или нет. Для этого будем постоянно сравнивать текущие очки с рекордом, и если текущие больше — установим новый рекорд и запишем имя победителя:
Запоминаем рекорды
Сейчас у игры есть существенный недостаток — если открыть страницу заново в том же браузере, она не вспомнит имя чемпиона. Когда мы делали свой туду-лист на JavaScript, то использовали для этого локальное хранилище браузера — localstorage. При новом открытии страницы можно будет взять данные о рекорде оттуда.
Возьмём из той статьи наш код для локального хранилища и поправим его под нынешнюю задачу — хранить имя игрока и его рекорд. Поставим этот код сразу после того, как спросим имя игрока на старте:
Но в хранилище ничего не появится автоматически — мы сами должны положить туда значение рекорда и имя чемпиона. Сделаем это в том же разделе, где мы начисляем очки за линии. Поправим немного, чтобы код выглядел так:
Теперь при каждом обновлении рекорда в хранилище сразу будет записываться актуальная информация. Даже если мы обновим страницу, записи останутся:
Добавляем сложность и уровни
Чтобы играть было интереснее, сделаем так: с каждым новым уровнем фигуры будут падать всё быстрее. Для этого находим в коде строчку, которая отвечает за скорость движения фигур вниз и правим её следующим образом:
// фигура сдвигается вниз каждые 36 кадров минус значение текущего уровня. Чем больше уровень, тем быстрее падает.
Логика тут такая: чем выше уровень, тем меньше интервал обновления между сдвигами, что даёт нам ощущение повышенной скорости. Хотя на самом деле фигуры не падают быстрее, просто они меньше тупят.
Например, на первом уровне фигура сдвигается на одну клетку вниз каждые 35 кадров, а на 10 уровне — каждые 25 кадров, на треть быстрее.
Сами уровни будем считать там же, где и очки. Чтобы перейти на новый уровень, нужно набрать 100 очков. Зная это, легко получить значение уровня — достаточно разделить нацело количество очков на 100 и прибавить 1. Такой подход и даст нам нужный уровень.
Запишем это там же, где и идёт подсчёт очков:
level = Math.floor(score/100) + 1;
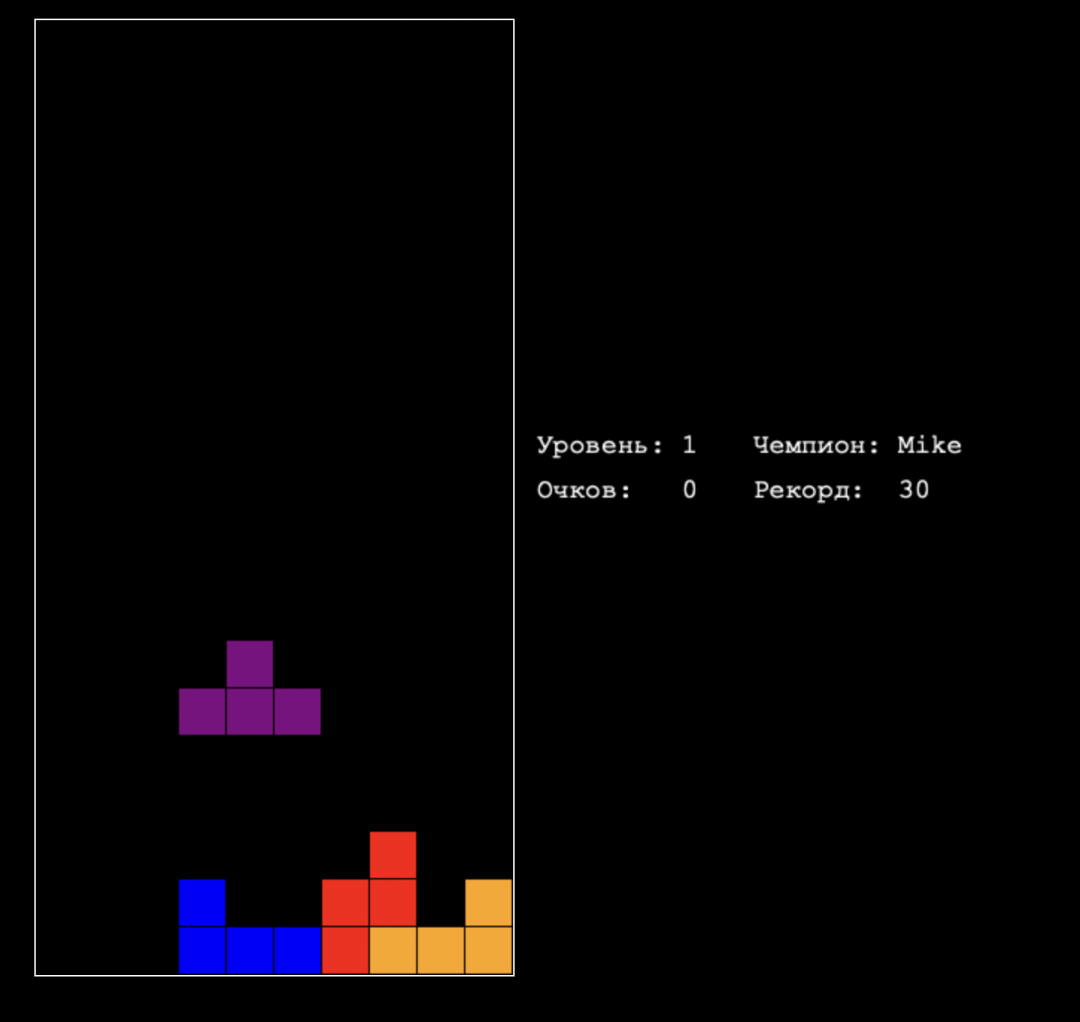
Теперь всё в порядке. Можете скопировать код себе или поиграть на странице проекта.
Как я научил ИИ играть в Tetris для NES. Часть 2: ИИ
Первая часть (анализ кода) находится здесь: https://habr.com/post/420725/.
Алгоритм
Описание
Алгоритм непрерывно выполняет следующие шаги:
Поиск блокировки
Рассмотрим упрощённую версию Tetris, в которой фигуры не падают автоматически. Единственный способ спустить фигуру вниз — это мягкий спуск. Убрав из игры тайминги, мы можем полностью описать состояние активного тетримино его позицией и ориентацией. Фигура имеет известное место изначального создания, а для преобразования из одного состояния в другое используются следующие операции:
Множество заблокированных состояний с минимальной последовательностью создающих их операций можно найти с помощью поиска в ширину (breadth-first search, BFS). Как сказано ниже, для хранения промежуточных результатов он использует очередь.
Поле visited помечается, когда состояние занесено в очередь. В BFS это допустимо, потому что каждое последующее состояние увеличивает общую длину пути на 1. То есть увеличением длины пути невозможно создать последующее состояние, которое нужно вставить куда-то, кроме конца очереди для сохранения порядка.
Поле predecessor указывает на объект состояния, из которого происходит текущее состояние. Оно задано, когда состояние занесено в очередь. Состояние создания не имеет предшествующих состояний.
Трёхмерный массив объектов состояний, очередь и BFS упакованы в класс. У него есть метод поиска, получающий игровое поле (двухмерный массив), тип тетримино и слушателя. Каждый раз, когда обнаруживается блокированное состояние, игровое поле обновляется, добавляя тетримино в соответствующее место. Затем изменённое игровое поле вместе с информацией об изменениях передаётся слушателю для обработки. После того, как слушатель выполнит возврат, игровое поле восстанавливается.
Слушатель используется для объединения нескольких операций поиска в цепочку, что даёт возможность нахождения всех возможных способов добавления двух (или более) тетримино на игровое поле. Первый поисковик в цепочке выполняет BFS только один раз. Однако второй поисковик выполняет BFS каждый раз, когда первый поиск обнаруживает заблокированное состояние. И так далее, если в цепочке присутствуют и другие поисковики.
Слушатель последнего поисковика оценивает изменившееся игровое поле. Когда он находит игровое поле лучше того, что было исследовано ранее, он записывает используемый объект заблокированного состояния, который в это время использует первый поисковик в цепочке. Поскольку первый поисковик выполняет BFS только один раз, поля predecessor его объектов состояния остаются правильными до завершения всего процесса поиска. То есть последний слушатель по сути записывает путь, по которому должно пойти первое тетримино, чтобы в результате прийти к наилучшей конфигурации игрового поля.
Оценочная функция
Изменённому игровому полю оценочная функция присваивает значение — взвешенную сумму различных влияющих параметров. Используемая в этом случае оценочная функция основана на функции, разработанной Исламом Эл-Аши. В ней используются следующие параметры:
Эти идеи применены в описанной ниже версии на Java; она выполняется за пределами FCEUX и её можно настроить для неграфической, расположенной в памяти игры, работающей с гораздо более высокой скоростью. После подготовки PSO я удивился, увидев, что алгоритм не движется дальше после начальной итерации. После этой итерации несколько случайно сгенерированных вариантов решения уже играли достаточно хорошо. В течение нескольких дней размер этого множества снижался, пока не остался только один вариант. Вот значения для этого решения:
| Параметр | Вес |
|---|---|
| Общее количество очищенных рядов | 1.000000000000000 |
| Общая высота блокировки | 12.885008263218383 |
| Общее количество ячеек-колодцев | 15.842707182438396 |
| Общее количество отверстий в столбцах | 26.894496507795950 |
| Общее количество переходов в столбцах | 27.616914062397015 |
| Общее количество переходов в строках | 30.185110719279040 |
Игровое поле оценивалось умножением параметров на соответствующие им веса и сложением результатов. Чем ниже значение, тем лучше решение. Поскольку все параметры и веса имеют положительные значения, то все параметры вредят общей оценке; каждый из них необходимо минимизировать. Также это означает, что наилучшая оценка равна 0.
Поскольку эти веса выбирались случайным образом, диапазон подходящих значений может быть очень широк. Этот конкретный набор чисел и предполагаемая относительная важность каждого параметра могут быть несущественными. Тем не менее, интересно будет за ними внимательно понаблюдать.
Наименее вредящий параметр — это общее количество очищенных рядов. Сам факт того, что этот параметр вредит, контринтуитивен. Но основная цель ИИ — это выживание. Он не стремится к наибольшему количеству очков. Вместо этого он играет консервативно, обычно очищая ряды по одному. Для получения Double, Triple или Tetris придётся выращивать кучу, что идёт вразрез с долговременной целью.
Следующей в списке идёт общая высота блокировки. Её можно минимизировать, опуская тетримино как можно ближе к полу. Это простая стратегия, вносящая свой вклад в долговременной перспективе в выживание, а в кратковременной перспективе — в качественную упаковку фигур.
Вес, назначенный общему количеству ячеек-колодцев, кажется немного удивительным, потому что опытные игроки обычно намеренно строят глубокие колодцы, чтобы набрать несколько Tetris (комбинаций из четырёх линий) подряд. Но как сказано выше, это рискованная игра, противоречащая основной цели — выживанию. Кроме того, количество колодцев является показателем «неровности» кучи. Определённый уровень неровности идёт на пользу при размещении определённых фигур или комбинаций фигур. Но высокая неровность причиняет ущерб плотной упаковке.
Общее количество отверстий в столбцах равно примерно половине от общего количества переходов в столбцах. Эти параметры можно скомбинировать и свернуть в общий связанный параметр, получив более обширный и наиболее вредный параметр: общее количество переходов.
Области плотной упаковки имеют во всех направлениях малое количество переходов. Поэтому основную стратегию, движущую искусственным интеллектом, можно вкратце описать так: упаковывать фигуры как можно более близко друг к другу.
Другие параметры
Вот список ещё нескольких параметров, с которыми я экспериментировал в процессе разработки ИИ:
Ещё одним полезным фактором является значение смещения. Например, совершенно плоская поверхность кучи имеет дисперсию высот столбцов 0. Но идеально плоская поверхность не адаптируется под S и Z, а также другие сочетания фигур. Следовательно, с помощью вычитания константы дисперсию необходимо центрировать около оптимальной неровности.
Настроенные и смещённые параметры можно возводить в какую-нибудь степень, чтобы перед вычислением взвешенной суммы они могли масштабироваться логарифмически или экспоненциально. Все эти вероятности можно рассматривать как дополнительные веса, которые потенциально можно оптимизировать методами наподобие PSO.
Многие из параметров дают понимание того, насколько хорошо куча сможет управляться с дополнительными фигурами, например, те, которые имеют дело с неровностью поверхности, но «Общая величина адаптации», «Средняя оценка следующей фигуры» и «Усреднённая симулируемая игра» оценивают изменённое игровое поле вставкой фигур, не входящих в две известные. При исследовании последующих фигур из-за быстрого устранения рядов количество полученного дополнительного знания уменьшается с глубиной. Это значит, что давно прошедшее течение партии не так важно, и течение партии в далёком будущем тоже не очень важно. На самом деле, если короткая последовательность фигур случайным образом поставлена неправильно, то ИИ быстро восстанавливает ход игры, используя несколько следующих фигур для очистки затронутых рядов. Определение оптимальной величины анализа последующих фигур требует дальнейших исследований.
Ещё одним аспектом полезности параметра являются вычислительные затраты. Затраты сильно увеличиваются, потому что оценочная функция вызывается для каждого возможного размещения двух фигур. Поскольку ИИ должен уметь играть в Tetris в реальном времени, затратные факторы, предоставляющие ценную информацию, можно обменять на более приближенные техники, которые выполняются быстрее.
Обучение ИИ
Существуют патологические последовательности, которые способны привести к Game Over вне зависимости от стратегии. Простейший пример — это бесконечная последовательность тетримино S и Z, которая, как показано в анимации, быстро приводит ИИ к проигрышу.
Поскольку для прогона варианта ИИ до завершения нескольких партий и вычисления среднего нужны дни, совершенно непрактично использовать как метрику управления PSO среднюю длительность партии. Вместо этого можно с контролируемой скоростью увеличивать сложность игры, повышая частоту S и Z, что со временем приведёт к попеременному созданию только этой пары фигур.
Я попробовал использовать этот метод обучения, но обнаружил, что обучение ИИ работе с частыми S и Z на самом деле вредит способности справляться с равномерно распределёнными случайными фигурами.
В альтернативном методе, на который меня вдохновила игра B-Type, управляющей PSO метрикой является частота очистки рядов. Игровое поле представляет собой схему из 10 строк случайных мусорных блоков, и при каждой очистке строки снизу появляется новая строка мусора, восстанавливая высоту кучи. Так как игровое поле имеет ширину 10 столбцов, а каждое тетримино состоит из 4 квадратов, то в среднем AI должен очищать ряд через каждые 2,5 тетримино. А чтобы избавляться от мусора, он должен делать это ещё быстрее.
К сожалению, эта техника тоже не улучшила производительность. Одна из вероятных причин заключается в том, что случайные дыры в мусоре не точно соответствуют тем строкам, с которыми ИИ имеет дело в настоящем игровом процессе. Кроме того, очистка ряда — это кратковременная цель; жадная очистка рядов необязательно улучшит долговременное выживание. Время от времени ряды не стоит трогать, чтобы обрабатывать определённые комбинации последующих фигур.
На своей веб-странице Колин Фэй предложил другой подход. Он создал гистограммы, отображающие процент фигур, блокируемых в каждой строке во время пробных партий. Интересно, что все гистограммы выглядят практически идентично вне зависимости от количества созданных фигур. Исходя из этого, он предположил, что можно использовать приближенное изображение функции для любой пробной партии при оценке статистического ожидания блокировки фигуры в строке создания, получив таким образом время, в течение которого ИИ будет играть до конца игры. Я решил исследовать эту возможность.
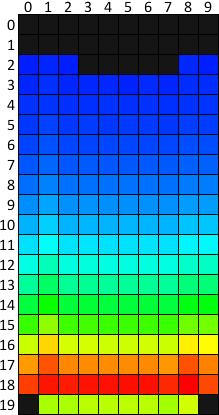
Ниже показана тепловая карта множества пробных партий, в сумме содержащих 2 039 900 000 тетримино. Каждая ячейка раскрашена на основании процента заблокированных в ней фигур. Для усиления визуального контраста выбрана нелинейная палитра. Карта была создана нормализацией значений ячеек с помощью деления на максимальный процент ячеек, а затем возвещением в степень 0,19 (см. «гамма-коррекция»).
| Цвет | Процент |
|---|---|
| ■ | 0.00000000 |
| ■ | 0.00000315 |
| ■ | 0.00024227 |
| ■ | 0.00307038 |
| ■ | 0.01860818 |
| ■ | 0.07527774 |
| ■ | 0.23582574 |
| ■ | 0.61928352 |
| ■ | 1.42923040 |
| ■ | 2.98867416 |
| ■ | 5.78182519 |
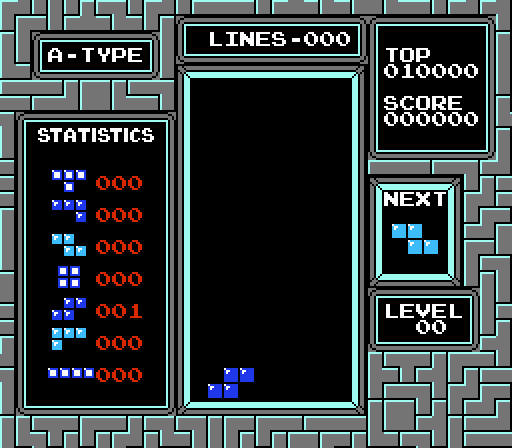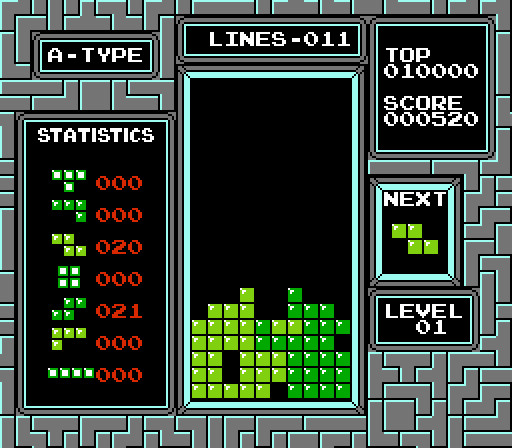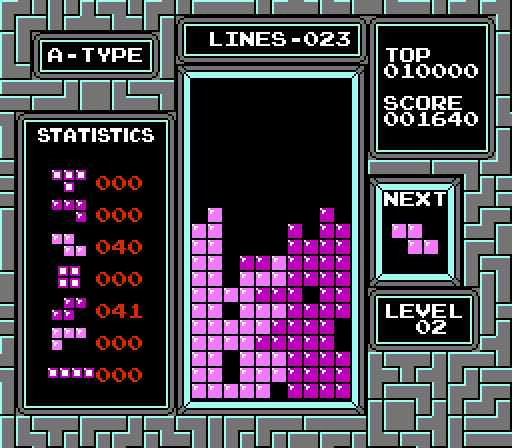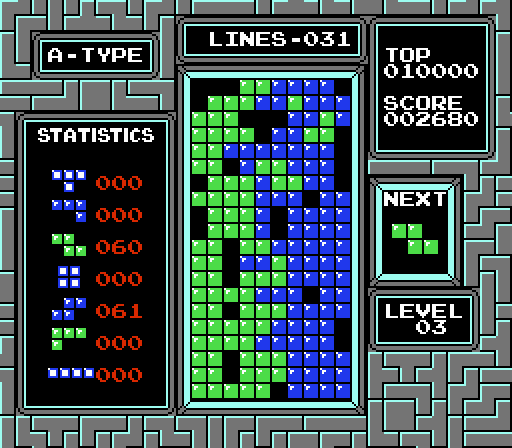
Тёмно-оранжевая и красная полоса в строках 17 и 18 означает, что подавляющее большинство фигур в результате оказываются там. Бледно-зелёный оттенок снизу — следствие геометрии фигур: только 4 из 7 типов тетримино могут оказаться в нижней строке. Нижние углы чёрные, потому что там невозможно оказаться.
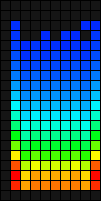
Цвет вдоль каждой строки практически однороден, и это позволяет предположить, что горизонтально фигуры распределяются равномерно. Незначительные разрывы можно объяснить, посмотрев на гистограммы отдельных типов фигур:
T оказывается наиболее универсальным типом: его гистограмма более равномерна, чем у всех остальных. Аномалии в гистограмме J — результат влияния стенок; только Jr и Jl могут находиться в боковых столбцах, что заставляет ИИ для компенсации чаще использовать столбцы 1 и 9. То же самое относится и к L. Гистограммы Z и S выглядят примерно одинаковыми, что подчёркивает дисбаланс из-за того, что Zv и Sv не являются идеальными зеркальными отражениями друг друга. Тип O ограничен игровым полем 19×9, и похоже, что ИИ склонен чаще использовать O по бокам, чем в центре. Тетримино I сдвинуто вправо, потому что там расположена его исходная точка; поэтому блокировка в столбце 1 случается редко.
В таблице показано процентное соотношение фигур, блокируемых в каждой строке.
| Строка | Процент |
|---|---|
| 0 | 0.0000000000 |
| 1 | 0.0000000000 |
| 2 | 0.0000004902 |
| 3 | 0.0000026472 |
| 4 | 0.0000066180 |
| 5 | 0.0000172557 |
| 6 | 0.0000512280 |
| 7 | 0.0001759400 |
| 8 | 0.0006681210 |
| 9 | 0.0023187901 |
| 10 | 0.0077928820 |
| 11 | 0.0259672043 |
| 12 | 0.0866187068 |
| 13 | 0.2901315751 |
| 14 | 0.9771663807 |
| 15 | 3.3000408353 |
| 16 | 10.6989059268 |
| 17 | 28.5687976371 |
| 18 | 50.0335706162 |
| 19 | 6.0077671454 |
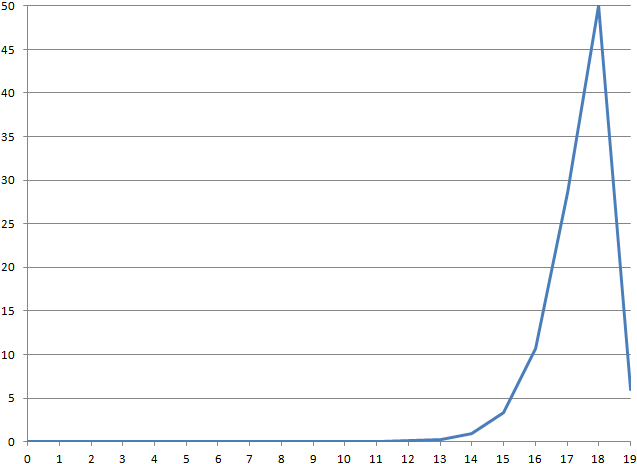
Вот график значений:
Если не учитывать строку 19, то график демонстрирует экспоненциальный рост.
Ниже показан список соотношений количества заблокированых фигур в соседних строках.
| СтрокаA/Строка B | Соотношение (%) |
|---|---|
| 1/2 | 0.00 |
| 2/3 | 18.52 |
| 3/4 | 40.00 |
| 4/5 | 38.35 |
| 5/6 | 33.68 |
| 6/7 | 29.12 |
| 7/8 | 26.33 |
| 8/9 | 28.81 |
| 9/10 | 29.76 |
| 10/11 | 30.01 |
| 11/12 | 29.98 |
| 12/13 | 29.85 |
| 13/14 | 29.69 |
| 14/15 | 29.61 |
| 15/16 | 30.84 |
| 16/17 | 37.45 |
| 17/18 | 57.10 |
| 18/19 | 832.81 |
В строках 16–19 учитываются фигуры, взаимодействующие с полом игрового поля, поэтому их можно отбросить. В строках 0–5 слишком выборка слишком мала, чтобы быть значимой. Оставшиеся соотношения, пары 6/7–14/15, почти идентичны; их среднее значение равно 29.24%. Это значит, что вероятность того, что куча вырастет на одну строку примерно одинакова вне зависимости от высоты кучи. Это вполне логично, потому что правила Tetris ограничивают вазаимодействия в вершине кучи при её плотной упаковке.
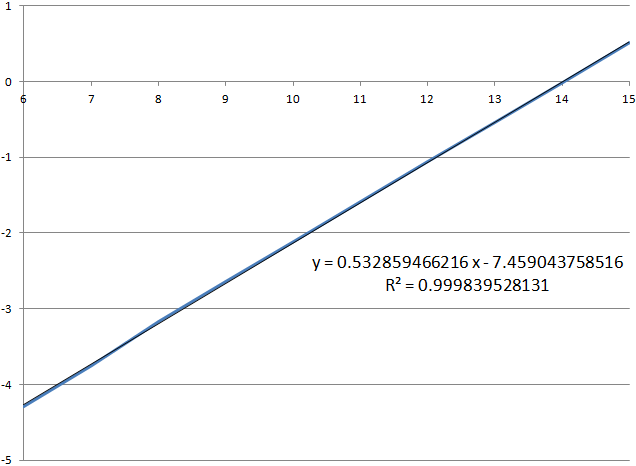
Ниже показан график log10 процентов фигур в строках 6–15.
Он близок к идеально прямой линии с близким к 1 коэффициентом детерминации. Формула, выведенная из показанной выше линейной регрессии, даёт нам пересечение с осью Y, предполагающее, что процент фигур в строке 0 приблизительно равен 10 −7.459 %. Величина, обратная этому значению, даёт нам статистическое ожидание в 2 877 688 349 тетримино или 1 151 075 340 рядов до конца игры.
Это даёт нам понять, что log10 процента фигур в каждой строке остаётся линейным вплоть до строки 0. Однако когда куча почти достигает потолка игрового поля, свобода перемещения ограничивается до такой степени, что это свойство нарушается. Кроме того, блокировка фигуры в строке 0 не обязательно означает game over; ещё можно спастись, если есть место для создания новых фигур.
Ещё один способ оценки силы ИИ заключается в измерении среднего количества созданных фигур между полными очистками игрового поля. Полную очистку можно получить всего с 5 тетримино. Например, среди прочих возможностей, этого можно добиться выложенными на полу игрового поля пятью фигурами O. В общем случае, поскольку каждое тетримино состоит из 4 квадратов, а ширина игрового поля — 10 квадратов, то количество созданных фигур между полной очисткой должно быть кратным 5 (так как 4×5n = 2×10n).
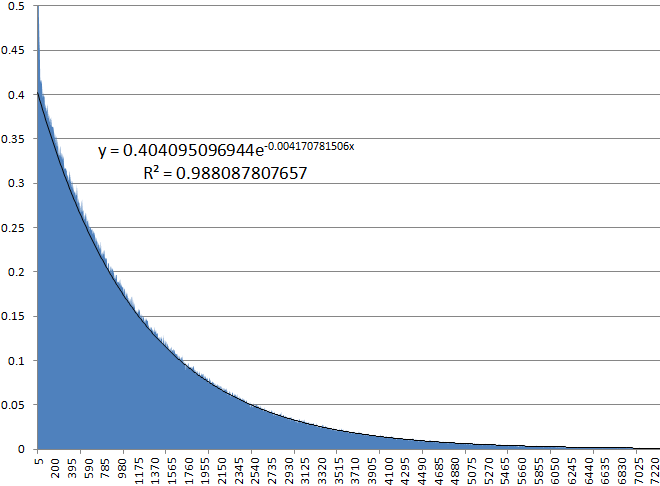
На гистограмме ниже показана вероятность (в процентах) того, что ИИ достигнет полной очистки поля после указанного количества созданных фигур.
Порядок степени в показанной выше формуле определяет скорость убывания и, предположительно, силу ИИ. Согласно этой формуле, примерно 0,4% или около 1 из 253 партий, начинающихся с пустого игрового поля, завершаются полной очисткой через всего 5 тетримино.
В противоположность тому, что предпололожил Фэй, константы в линейном и экспоненциальном приближениях требуют очень большого размера выборки, чтобы R 2 приблизилось к 1, поэтому этот способ неприменим для PSO. Однако константы, полученные при долгих партиях, можно использовать для оптимизации функции аппроксимации, создающей возможные значения констант при коротких партиях. В своего рода петле обратной связи разработки оптимизированную функцию аппроксимации можно использовать в PSO, который усовершенствует ИИ, который в свою очередь можно использовать для вычисления новых констант, служащие в качестве эталонных критериев для функции аппроксимации.
Версия на Java
О программе
Для разработчиков, незнакомых с Lua, я добавил в zip-файл с исходниками порт ИИ на Java. Классы являются почти построчной трансляцией объектов Lua на основе замыканий.
Пакеты
Код разделён на два пакета:
Классы и интерфейсы ИИ
Класс с соответствующим названием Tetriminos описывает тетримино. Он используется подобное enum и содержит константы для всех типов тетримино:
NONE означает неназначенное значение. Оно используется для пустых ячеек игрового поля.
Хотя в Java есть богатый Collections API, Searcher содержит собственную реализацию очереди. Класс Queue использует State.next для соединения объектов State в связанный список. Поскольку все объекты State определены предварительно, а каждый State может быть внесёт в очередь не больше одного раза, то очередь может работать на месте, что позволяет отказаться от излишних временных объектов-контейнеров, используемых в общих реализациях очереди.
Он порождает очередь с состоянием созданного тетримино, а затем последовательно извлекает дочерние элементы из выведенных из очереди состояний, добавляя их обратно в очередь, когда они появляются на игровом поле.
В метод search передаются игровое поле, содержащее сочетание занятых и пустых ячеек, создаваемый тип тетримино и произвольный идентификатор. В процессе выполнения BFS при каждом обнаружении позиции блокировки вызывается слушатель.
Когда слушатель получает изменённое игровое поле, он вызывает PlayfieldUtil.clearRows для удаления заполненных рядов; метод распознаёт их, сверяясь со значением в дополнительном элементе массива. Для удаления строки код пользуется тем фактом, что в Java двухмерные массивы по сути являются массивами массивов; он просто сдвигает вниз ссылки на строки. PlayfieldUtil содержит свободные строки; он завершает процесс очистки, вставляя вверх ссылку на одну из них. Перед выполнением сдвига индекс очищаемой строки сохраняется в дополнительный элемент строки. Затем ссылка на строку записывается в стек.
Потом слушатель вызывает PlayfieldUtil.restoreRows для отмены изменений, внесённых в игровое поле. Шаги отменяются в обратном порядке. Сначала получается свободная строка из вершины. Затем из стека извлекается заполненная строка и восстанавливается индекс из дополнительного элемента. Он используется для сдвига ссылок строк и для возврата на место удалённой строки. Наконец, восстанавливается дополнительный элемент, ему присваивается значение ширины игрового поля — количества занятых ячеек в заполненном ряду.
Вызов ИИ
Поскольку версия на Java не привязана к FCEUX, потенциально её можно использовать для других проектов. Для тех, кому интересно интегрировать ИИ куда-нибудь ещё, в этом разделе описывается всё необходимое.
Заполним массив типов тетримино типами изначально создаваемой фигуры и следующей фигуры, которые в обычном случае выбираются вручную.
Перед повторным вызовом AI.search необходимо случайным образом выбрать следующее тетримино.
Всё вместе это выглядит следующим образом:
Вместо вывода игрового поля в текстовом виде можно использовать более интересный способ отображения происходящего…
Отображение игрового поля
Класс TetrisFrame имитирует графику Nintendo Tetris, в том числе особенности поведения, описанные в предыдущей части статьи.
TetrisFrame имеет 4 метода для манипулирования экраном. Метод displayTetrimino рендерит активное тетримино в указанных координатах. Он получает параметр задержки, заставляющий метод ждать перед возвратом указанное количество кадров анимации.
Метод lockTetrimino блокирует фигуру на месте. Соответствующим образом обновляются счётчик рядов, очки, уровень и цвета тетримино, демонстрируя ожидаемое любопытное поведение при превышении значениями допустимых значений. Присвоение параметру animate значения true включает анимации очистки рядов и мерцание экрана при получении Tetris. Метод блокируется до завершения анимации.
updateStatisticsAndNext выполняет инкремент счётчика статистики для нового созданного тетримино и обновляет отображение следующей фигуры.
ImageLoader содержит таблицу палитр NES, а в ImagePane хранится полный набор отображаемых значений уровней.
Другие проекты
Потенциально код можно использовать вместо записи для режима демо. На самом деле такое демо можно рендерить вечно, пользуясь тем, насколько быстро способен ИИ очищать всё игровое поле. Чтобы достичь этого, в генераторе псевдослучайных чисел нужно использовать в качестве seed некую произвольную константу, что даст нам детерминированную последовательность тетримино. Будут записаны первые два тетримино последовательности. Когда ИИ достигнет полной очистки поля, следующие два тетримино будут сравниваться с первыми двумя из последовательности. Если они совпадают (это событие ожидается через каждые 49 полных очисток поля), то генератору псевдослучайных чисел можно передать в качестве seed ту же константу, что создаст бесконечный цикл демо. Длительность цикла может быть очень большой, чтобы скрыть сам факт того, что это цикл. Кроме того, демо может начинаться со случайной точки цикла, создавая каждый раз новое демо.
Чтобы проверить его в работе, внесите в Main следующие изменения:
WellFilter работает, но не особо эффективно. Он содержит простую эвристику, предназначенную для демонстрации концепции. Чтобы получать Tetris чаще, нужно использовать более изощрённую стратегию, возможно такую, которую можно оптимизировать с помощью PSO.
PatternFilter строит изображения построчно снизу вверх, аналогично тому, как работает WellFilter ; однако вместо оберегания самого правого столбца PatternFilter одобряет только дочерние состояния, соответствующие определённому паттерну.
Показанная выше строка кода создаёт силуэты семи типов тетримино.
Ещё один пример с большим тетримино T, повёрнутым под углом.
Ещё один пример. Если приглядеться, то вы увидите название игры.
Версия с геймпадом
Скрипт на Lua и программа на Java игнорируют гравитацию; для них скорость спуска не важна, потому что в зависимости от конфигурации они или телепортируют фигуры сразу на нужное место, или перетаскивают вдоль любого выбранного пути. В каком-то смысле они просто имитируют Tetris, а не играют в него. Однако в zip-файле с исходниками есть другой скрипт на Lua, который играет с помощью генерации сигналов кнопок геймпада, что позволяет игре управлять перемещением фигур, гравитацией и всем остальным.
Добавление гравитации сильно расширяет пространство поиска, заставляя ИИ учитывать хитрые правила манипуляций с фигурами. Подробности этих правил описаны в первой части статьи, и могут быть полностью оценены непосредственным изучением кода. Вот самые важные из них:
ИИ использует объект State со следующими полями:
С другой стороны, для мягкого спуска нужно первоначально зажать на три кадра кнопку «Вниз», что требует существования 4 состояний:
На самом деле в коде на Lua используется целочисленная константа, но принцип тот же.
Каждый Searcher предварительно определяет 8-мерный массив, содержащий все возможные состояния ( 20 строк × 10 столбцов × 4 поворотов × 2 Влево × 2 Вправо × 4 Вниз × 2 A × 2 B ), а BFS выполняется аналогично методу, показанному для трёхмерного массива. В показанном ниже псевдокоде описано, как из выведенных из очереди состояний получаются последующие состояния.
Как показано в изложенном ниже псевдокоде, функция addChild учитывает порядок событий, происходящих в каждом кадре (например, сдвиг, поворот и спуск).
Хотя пространство поиска значительно уменьшено благодаря описанным выше ограничениям, для выполнения поиска всё равно требуется 1–3 секунды. Если запустить его, то вы заметите паузу после создания каждого тетримино. Кроме того, движения выглядят очень неестественно; обычно поворот выполняется за мгновение до блокировки. Тем не менее, этот ИИ играет почти так же, как игнорировавшая гравитацию версия, даже на максимальной скорости.
Более простой способ учёта гравитации заключается в ограничении движения фигур только поворотом, за которым следует сдвиг, а затем спуск до самого дна. Идея заключается в том, что если избавиться от скольжения и прокручивания, то вертикальная скорость движения фигур будет мало влиять на ИИ; всё, что ему будет нужно — доставить фигуру в нужный столбец, а остальным займётся гравитация. Ещё одно преимущество этой техники в том, что пространство поиска очень мало, что позволяет играть в реальном времени, без задержке для вычислений. Однако недостаток такого подхода в том, что без скольжений и прокручивания ИИ играет гораздо хуже. Тем не менее, ИИ «Тетриса», неспособный играть в реальном времени, практически бесполезен.
Дополнение
Ранее я написал плагин, процедурно имитировавший игрока в «Тетрисе». Однако мой проект обладал некоторыми недостатками:
Видео
Понаблюдайте за тем, как бот набирает максимальное количество очков Nintendo Tetris, начиная с уровня 19 во всех показанных ниже видео.
Скачивание
Запуск
Предварительные требования
Запуск плагина
Задание скорости
Чтобы игра шла быстрее, выберите Machine | Speed | Max.
Подробности
Плато
Ниже уровня 10 скорость спуска на каждом уровне слегка выше, чем на предыдущем. Но на уровне 10 и выше есть несколько плато, на которых в течение нескольких уровней скорость остаётся постоянной. Это следствие способа работы механизма спуска. Скорость представлена в виде количества кадров на спуск, что является целочисленным значением. То есть для более высоких уровней остаётся не так много вариантов: 10–12, 13–15, 16–18, 19–28 и 29+ это 5, 4, 3, 2 и 1 кадр на спуск.
Бот разрабатывался с учётом только плато 19–28. В чётных кадрах он нажимает на геймпаде «Влево», «Вправо», A, B или ничего. А в нечётных кадрах он позволяет осуществлять автоматический спуск, не нажимая никаких кнопок. Похоже, что игра не воспринимает горизонтальное движение, совпадающее с поворотом; поэтому каждая кнопка нажимается независимо в чётных кадрах.
В отличие от мастеров, играющих на больших уровнях, бот не пользуется преимуществом отложенного автосдвига (Delayed Auto Shift, DAS), известного так же как «автоповтор», и связанные с ним техники. Его работа больше напоминает технику вибрирующего большого пальца Тора Акерлунда. Однако он увеличивает частоту вибрации до теоретического максимума, допускаемого игрой.
Игроков вознаграждают 40, 100, 300 и 1200 очками за Single, Double, Triple и Tetris. А значения очков умножаются на номер уровня плюс 1. Другими словами, для получения максимального счёта игрок должен стремиться к максимальному количеству Tetris, как можно дольше играя на высоких уровнях.
Уровень 19 является наибольшим, который можно выбрать в качестве начального, что позволяет боту перепрыгнуть сразу к плато 19–28. Однако из за бага в механизме подсчёта уровней, о котором я говорил в предыдущей части, игра перейдёт на уровень 20 после очистки 140 рядов, вместо ожидаемых 200. После этого игра будет менять уровни каждые 10 рядов. Однако после достижения 230 рядов бот поднимется с плато и быстро сдастся. То есть ему нужно набрать как можно больше Tetris до очистки 230 рядов.
Мягкий спуск
Мягкий спуск тоже может увеличить количество очков. Для получения очков фигуру необходимо мягко спустить вниз до блокировки на игровом поле. Любой кратковременный мягкий спуск, происходящий по пути при позиционировании фигуры, не повлияет на счёт. При успешном спуске игрок получит по одному очку за каждую пересечённую при мягком спуске строку. И получившееся значение не умножается на номер уровня, даже если мягкий спуск приводит к очистке рядов.
Мягкий спуск оказывает незначительное влияние на общий счёт. Тем не менее, при возможности бот завершает размещение фигуры, нажимая «Вниз» для получения этих очков. В редких случаях он может усреднять разность между очень высоким счётом и превышением максимального значения очков.
Алгоритм ИИ
При создании фигуры бот исследует каждое возможное размещение текущей и следующей фигур. Допустимое размещение — это позиция, в которой фигура опирается или на занятые ячейки, или на пол игрового поля. Из места создания фигуры этой позиции можно достичь через последовательность горизонтальных перемещений, поворотов и спусков. Допустимые размещения и последовательности путей к ним находятся с помощью BSF.
Каждое из комбинированных последствий передаётся в оценочную функцию, которая вычисляет содержимое игрового поля. Комбинация с наименьшей оценкой выигрывает и текущая фигура размещается соответствующим образом. Результаты цепочки поиска влияют только на текущую фигуру. При создании следующей фигуры она оценивается в комбинации со следующей за ней фигурой, и так далее.
Оценочная функция
Оценочная функция — это взвешенная сумма следующих параметров:
Машинное обучение
Для нахождения весов оценочной функции использовался вариант метода роя частиц (Particle Swarm Optimization, PSO), описанный в сноске [1]. Для получения хорошего сходящегося поведения применены предложенные коэффициенты инерции и ускорения. А максимальные размеры шагов частиц определены ограничением их величин скоростей.
В процессе каждой итерации частицы оценивались параллельно, чтобы полностью использовать имеющиеся вычислительные ресурсы. Кроме того, после обнаружения сходимости (отсутствие улучшений после определённого количества итераций), PSO настраивался на автоматический перезапуск со случайно выбранными весами, что позволило ещё больше исследовать пространство поиска.
Каждый вектор позиции частицы оценивался симуляцией выполнения 100 партий на плато уровней 19–28. Полная партия подразумевает очистку 230 рядов, но многие завершались переполнением поля. Оценки партий сортировались, и оценка частиц определялась как среднее для 33 из 100 партий. Идея заключалась в выборе на основе агрессивности. Частицы в верхней трети привыкают только к желательным последовательностям фигур, что ограничивает необходимость консервативной игры. В результате они стремятся подталкивать обычную игру к грани, дожидаясь следующей «палки».
Последовательности фигур для 100 партий были сгенерированы до выполнения PSO, и одни и те же последовательности использовались снова и снова. Это было необходимо для фиксации пространства поиска, для того, чтобы варианты решения можно было сравнивать друг с другом. Последовательности создавались с помощью логики настоящего PRNG Nintendo Tetris, который предназначен для снижения шансов идущих друг за другом дубликатов. Но у PRNG тоже есть слабые места (см. раздел «Выбор тетримино» из предыдущей статьи): он не подбирает фигуры равномерно.
Первоначальные попытки давали ботов, действующих слишком агрессивно. Если они одолевали плато 19–28, то обычно добирались до максимального счёта. Но, к сожалению, они часто слишком рано приводили к переполнению поля. В ответ на это для «успокоения» ботов было сделано четыре шага:
| Параметр | Вес |
|---|---|
| Общее количество очищенных рядов | 0.286127095297893900 |
| Общая высота блокировки | 1.701233676909959200 |
| Общее количество ячеек-колодцев | 0.711304230768307700 |
| Общее количество глубоких колодцев | 0.910665415998680400 |
| Общее количество отверстий в столбцах | 1.879338064244357000 |
| Общее взвешенное количество отверстий в столбцах | 2.168463848297177000 |
| Общее количество глубин отверстий в столбцах | −0.265587111961757270 |
| Минимальная глубина отверстий в столбцах | 0.289886584949610500 |
| Максимальная глубина отверстий в столбцах | 0.362361055261181730 |
| Общее количество переходов в столбцах | −0.028668795795469625 |
| Общее количество переходов в строках | 0.874179981113233100 |
| Общее количество высот столбцов | −0.507409683144361900 |
| Высота кучи | −2.148676202831281000 |
| Разброс высот столбцов | −1.187558540281141700 |
| Общее количество занятых ячеек | −2.645656132241128000 |
| Общее взвешенное количество занятых ячеек | 0.242043416268706620 |
| Дисперсия высот столбцов | 0.287838126164431440 |
Поскольку цепочка стремится к комбинации, минимизирующей оценочную функцию, параметры, имеющие положительные веса, можно считать бонусами, а остальные — штрафами. Но величины весов необязательно показывают значимость соответствующих параметров; они не нормализованы, поэтому их нельзя сравнивать.
Сила ИИ
Для оценки силы ИИ было собрано примерно 1,7 миллионов результатов (в очках) симулированных партий на плато 19–28. Оценка не отражает игру на уровне 29 или выше, и не учитывает очки, полученные от мягкого спуска. Однако в неё включены игры, преждевременно завершённые из-за переполнения поля. Для генерирования последовательностей тетримино использовалась логика PRNG Nintendo Tetris.
Среди этих результатов наибольшим счётом является 1 313 600. Минимальным — 0.
Среднее значение равно 816 379, и кажется, что это мало. Но как сказано ниже, данные искажены, поэтому лучшее представление о типичном значении даёт медианная оценка — 989 200 очков.
Как сказано выше, PSO оптимизировал веса на основании среднего значения из лучшей трети партий. В этом случае средний счёт лучшей трети равен 1 108 860. На самом деле средний счёт лучших 75% равен 1 000 000.
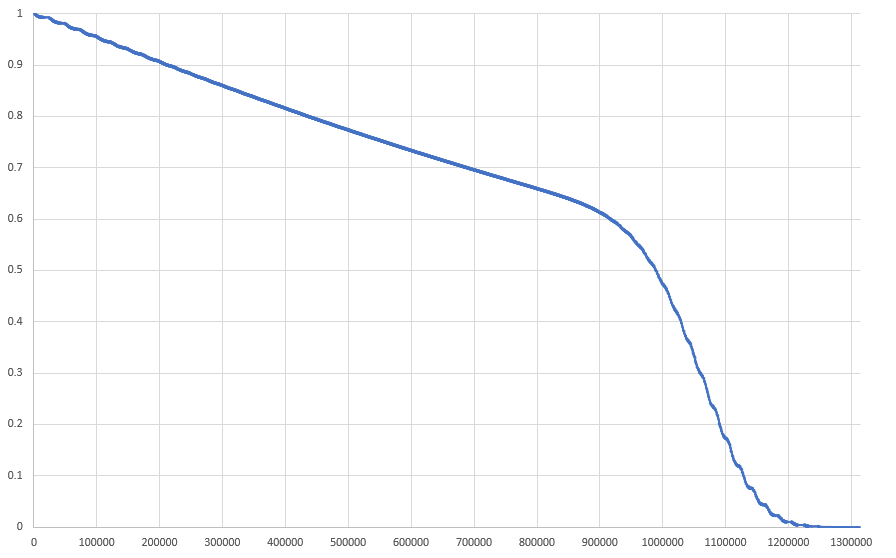
Бот имеет вероятность в 47% достичь предела очков до уровня 29. Он имеет вероятность в 61% получения 900 000 очков до уровня 29. На показанном ниже графике изображены вероятности набора очков до уровня 29.
Похоже, что вероятность линейно снижается примерно до 900 000 очков. Затем она переходит в перевёрнутую сигмоидную кривую.
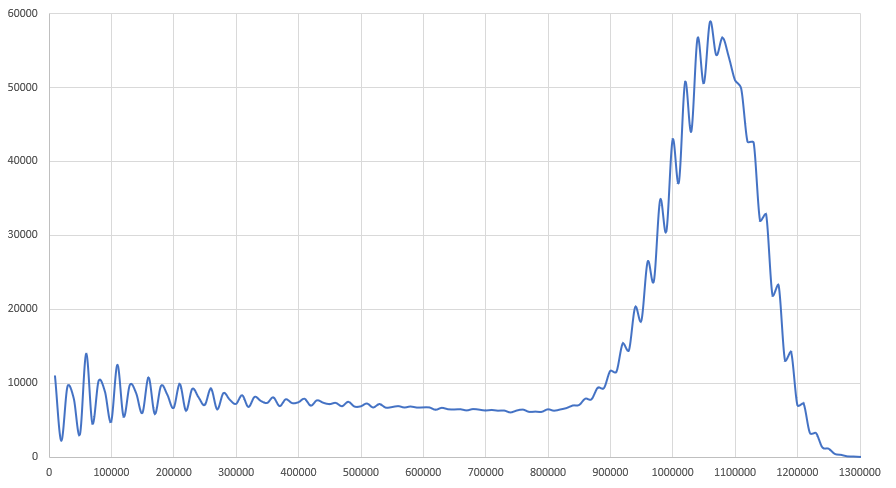
Ниже показана сглаженная гистограмма с количеством партий для каждого из набранных величин очков. Её форма определяется производной показанного выше графика.
Если игнорировать колебания, то примерно до 900 000 она плоская, а затем переходит в нормальное распределение с центром примерно возле 1 050 000 очков. Причины колебаний непонятны. Похоже, что количество очков предпочитает прыгать с шагом, кратным 20 000 очков. Возможно, это связано с циклом построения кучи и получения Tetris.