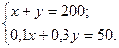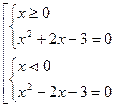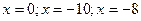Как сделать задачу двумя способами
Урок по математике «Решение задач разными способами»
Тема “Решение задач разными способами”
Вид: закрепление умения решать задачи на основе расширения способа действия.
Ход урока
1. Орг. момент.
Эмоционально-психологический настрой на урок. (Цель: создать эмоционально-психологический контроль)
Мне вспомнилась одна пословица “Корень ученья горек, да плод его сладок”. Как вы понимаете эту пословицу?
Она очень подходит к нашему уроку и вы это поймете.
2. Сообщение темы и цели урока.
— Тема нашего урока “Решение задач разными способами”
— Запишите число и тему урока.
3. Актуализация знаний.
— Мы с вами уже решали очень много самых разных задач, а сегодня я предлагаю вам решить необычные задачи, а задачи в которых есть буквенное значение.
4. Решение задачи.
Для ремонта школы привезли в одинаковых банках 90 кг зеленой краски и 180 кг белой краски. Зеленой краски было 18 банок. Сколько купили банок с белой краской?
1 способ.
1) 90 : 18 = 5 (кг) – в 1 банке.
2 способ.
1) 180 : 90 = 2 (раза) – во сколько раз за белую краску заплатили больше, чем за зеленую.
2) 18 х 2 = 36 (банок.)
— Ребята, что обозначает часть или целое число 90? 18? 180?
— Где мы еще с вами можем встретить часть и целое? (В уравнении)
5. Физминутка.
Если неизвестное число находится сложением – приседаете,
Вычитанием – руки вверх,
Делением – руки вперед.
А – 7 = 18 35 : а = 7 а + 6 = 10 30 – а = 13 а : 12 = 5 а х 4 = 24
— Назовите уравнения, где а – целое.
Решите уравнения второго столбика (по вариантам)
— Ребята, а что такое уравнение?
— А попробуйте теперь решить в паре такое уравнение:
6. Расширение способа действия.
— Мы с вами решали задачу двумя способами. Это были арифметические способы решения. А давайте попробуем решить эту задачу еще одним способом – с помощью уравнения.
— Что мы возьмем за х?
— Вы уже говорили, что уравнение это равенство. Какая величина в нашей задаче равна, одинаковая?
— Исходя из этих данных составьте в группах уравнение по этой задаче. (180 : х = 90 : 18)
— Молодцы! Это алгебраический способ решения задачи.
7. РРО.
— Мы с вами уже решали задачи разными способами, а сейчас попробуйте записать решение задачи в виде уравнения.
Уровень 1.
Реши задачу, составив уравнение.
На крыше сидело 7 голубей. Когда к ним прилетело еще несколько, их стало 15. Сколько голубей прилетело?
Уровень 2.
Реши задачу, составив уравнение.
В 7 одинаковых коробках 21 кг винограда. Сколько килограммов винограда в 4 таких же коробках?
8. Итог урока.
— Разрешите закончить наш урок, задав вам несколько вопросов.
— С чем мы сегодня познакомились на уроке?
9. Домашнее задание.
1 уровень. Найдите в учебнике задачи, которые можно решить уравнением.
2 уровень. Составьте 2 задачи, которые можно решить уравнением – простым и усложненным.
Конспект урока «Решения задачи 2 способами»
Решение задачи двумя способами.
Тип урока: урок открытия новых знаний
Цель: создать условия для развития умений решать задачи разными способами; формировать умение использовать различные формы записи условия задач.
Предметные: научатся решать задачи разными способами; сформировать умение использовать различные формы записи условия задач.
Познавательные: научатся находить способ решения учебной задачи и выполнять учебные действия в устной и письменной форме.
Регулятивные : принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями её реализации.
Коммуникативные: научатся сотрудничать со сверстниками и учителем через ИКТ.
Личностные: проявляют положительное отношение к школе и учебной деятельности; имеют представление о причинах успеха в учёбе; выражают этические чувства на основе анализа простых ситуаций.
I . Организационный момент.
-Здравствуйте, ребята. Откройте пожалуйста тетради и запишите:
II. Актуализация знаний.
1) 6 увеличить в 4 раза, полученное число уменьшить в 2 раза, полученное число увеличить на 18, полученное число уменьшить на 30.
2) 27 уменьшить в 3 раза, полученное число увеличить в 4 раза, полученное число увеличить на 4; сколько не хватает до 100?
3) 72 уменьшить в 9 раз, полученное число увеличить в 8 раз, увеличить на 36.
III. Постановка цели и задач урока.
‒ Сегодня мы будем учиться одну и ту же задачу решать разными способами.
Чтение, разбор условия и записи решений задачи № 847 по вопросам учителя:
‒ Как рассуждала Вера? Задайте вопросы к первому, ко второму и третьему действиям её решения.
В первом действии Вера узнала, сколько стоит 6 кустиков огуречной рассады.
Во втором действии Вера узнала, сколько стоит 2 кустика огуречной рассады.
Вера узнала сколько стоила вся рассада.
‒ Как рассуждал Дима? Задайте вопросы к первому и второму действиям его решения.
В первом действии Дима узнал сколько всего кустиков рассады купила мама.
Во втором действии Дима узнал сколько стоила вся рассада.
Сравнение обоих решений и выяснение, какой способ лучше.
-Какое решение лучше и быстрее?
IV .Первичное усвоение новых знаний
Решение задачи № 848 (1)
— Сколько цветочков из бисера делает Кристина за один урок? (6) А Даша?
Прочитаем условие задачи.
-Сколько цветочков сделают обе девочки за 6 уроков?
-Краткое условие задачи можно записать в виде текста, рисунка, таблицы.
Сегодня мы запишем краткую запись условия задачи в виде таблицы.
-Вопрос мы писать не будем, т.к. знак вопроса мы поставили в таблице.
— При разборе задачи № 847, мы увидели, что некоторые задачи можно решить несколькими способами! Давайте решим эту задачу в три действия.
-Что спрашивается в задаче? Что нам нужно знать, чтоб ответить на вопрос задачи? (Сколько цветочков делает Кристина за 6 уроков и сколько цветочков делает Даша за 6 уроков)
-Из тех данных, которые нам нужны, что нам известно и что нужно узнать?
(Нам известно, что Кристина за 1 урок делает 3 цветочка, а Даша 4. Но не известно сколько цветочков делала Кристина за 6 уроков и неизвестно сколько Даша делала цветочков за 6 уроков).
-Можно ли это узнать? Что нужно для этого сделать, чтобы узнать сколько цветочков за 6 дней сделала Кристина?
-Что нужно сделать, чтобы узнать сколько цветочков за 6 дней сделала Даша?
-Теперь мы можем ответить на вопрос задачи? Что нужно для этого сделать?
Решение задачи в 2 действии.
-Скажите, что мы можем узнать в первом действии? (Сколько цветочков сделали девочки за один урок)
— Что нужно сделать, чтобы ответить на этот вопрос? Нужно к 3 цветочкам прибавить 4 цветочка, получится 7 цветочков.
-Сколько уроков нужно было делать цветочки Кристине и Даше? 6 уроков
-А за один урок вместе, сколько они сделают цветочков? 7 цветочков.
-А как нам узнать, сколько они вместе сделают цветочков за 6 дней? Нужно по 7 цветочков взять 6 раз, получится 42 цветочка.
V .Первичная проверка понимания
Самостоятельное решение задачи № 848 (2) двумя способами.
— Дети, что вам на уроке понравилось?
-Какие задания вы бы хотели повторить на следующем уроке?
-Скажите, пожалуйста, что у вас вызвало затруднения?
-Спасибо за урок. Будьте здоровы. До свидания!
Номер материала: ДБ-1259959
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Решение задач разными способами. 2-й класс
Класс: 2
Задачи урока: закреплять умение решать задачи изученных видов разными способами; совершенствовать вычислительные навыки и навыки устного счёта; развивать внимание и логическое мышление.
Планируемые результаты
Предметные. Выполнять устные и письменные вычисления изученных видов в пределах 100. С помощью рисунка, схематического чертежа и краткой записи решать задачи. Распознавать и изображать геометрические фигуры. Использовать в речи название компонентов математических действий.
УУД (универсальные учебные действия)
Коммуникативные. Участвовать в диалоге, слушать и понимать других, высказывать свою точку зрения на события, поступки. Выполнят различные роли в паре, сотрудничать в совместном решении проблемы, управлять поведением партнёра.
Познавательные. Осознанное построение речевого высказывания в устной форме. Выделение и формирование учебной цели. Смысловое чтение; извлечение необходимой информации из текста. Самостоятельное создание алгоритмов деятельности при решении проблем. Обобщение, рассуждение и обоснование выводов.
Регулятивные. Самостоятельная организация своего рабочего места. Следовать режиму организации учебной деятельности. Определять цели учебной деятельности с помощью учителя. Составлять план и последовательность действий. Соотносить выполненное задание с образцом, предложенным учителем. Вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта сделанных ошибок. Стабилизация эмоционального состояния для решения различных задач.
Личностные. Выполнять задания поискового характера. Понимать учебную задачу и стараться её выполнить. Работа в парах. Отвечать на итоговые вопросы, подводить итог урока. Контролировать свою работу и её результат.
Оборудование: интерактивная доска, мультимедийный проектор, ноутбук учителя, ноутбуки учеников.
1. Организационный момент
– Создадим хорошее настроение себе и нашим гостям. Улыбнитесь друг другу и гостям, садитесь!
– Откройте тетради. Посмотрите свои достижения. Запишите число, классная работа.
Ну-ка, посмотри, дружок,
Ты готов начать урок?
Все ли на месте?
Всё ли в порядке?
Книжки, ручки, тетрадки, ноутбуки?
Все ли правильно сидят?
Все ли внимательно глядят?
2. Актуализация знаний
а) Логическая разминка.
Кто догадался, что надо сделать?
– Нарисуйте человечка в тетради.
Проверка. Вставить карточку с человечком в таблицу.
– У кого настроение улучшилось?
б) – Проиграем в круговые примеры.
– Какие примеры называются «круговыми»?
– Проверим, будут ли эти примеры «круговые».
34 – 20 6 + 28
74 – 70
12 : 2 14 + 30
44 + 30 4 * 3
– Почему эти примеры «круговые»?
3. Решение задач на нахождение третьего слагаемого.
а) – Что видите на рисунке? (Арбуз, тыкву, дыню)
– Сколько весит тыква? Дыня? Арбуз?
– Что обозначает число 12?
– Рассмотрите выражения на карточках.
3 + 5 12 – (3 + 5) 12 – 3 12 – 3 – 5
– Запишите в тетради выражение, с помощью которого можно узнать, сколько весят дыня и тыква.
– Запишите в тетради выражение, с помощью которого можно узнать, сколько весят арбуз и тыква.
– Запишите в тетради выражение, с помощью которого можно узнать, сколько весит арбуз.
12 – 3 – 5 = 4 (кг) 12 – (3 + 5) = 4(кг)
– Что можно сказать о двух последних выражениях? (Разные способы решения одной задачи)
– Кто может сформулировать тему урока? (Решение задач разными способами)
б) Решение задачи в тетради.
Один ученик решает задачу на доске.
– Прочитайте задачу.
– Как надо решить задачу. (Разными способами)
– Составим схематический чертёж к задаче.
Решим задачу, записав выражение.
25 – (5 + 8) = 12(с.) – прочитала вечером
Ответ: 12 страниц.
– Кто решил задачу другим способам?
25 – 5 – 8 = 12(с.) – прочитала вечером
– Как надо работать в парах?
– Включите ноутбуки (диск «Математика», 2 часть, с.76, 2 задание).
– Что надо сделать?
Проверка на интерактивной доске.
– Какого вида решали задачи? (Нахождение третьего слагаемого)
Физминутка для глаз.
Закрыть глазки, открыть.
Нарисовать глазками круг, треугольник.
4. Геометрическая задача
а) Какая фигура на доске? (Прямоугольник)
– Что такое прямоугольник?
б) Прочитайте задание на с.77
Выполнить задание самостоятельно.
Работа в парах. Посмотрите, как начертил прямоугольник сосед.
Проверить решение задачи разными способами. Записать каждый способ на доске.
(1 + 10) * 2 = 22 (см) – периметр прямоугольника
(1 * 2) + (10 * 2) = 22 (см) – периметр прямоугольника
1 + 1 + 10 + 10 = 22(см) – периметр прямоугольника
– Какого вида задачу повторили? (Нахождение периметра)
5. Рефлексия учебной деятельности
а) – Что повторили сегодня на уроке?
– Что больше всего запомнилось?
Решение одной задачи различными способами
В педагогической и методической литературе общепринятым является мнение, что решение задач разными способами является эффективным педагогическим приемом, поскольку это способствует повышению уровня математических знаний и умений учащихся, развитию их исследовательских способностей, пробуждает творческую фантазию и интерес к изучению математики.
Однако, если данный прием применять бессистемно и неорганизованно, решая каждый раз, когда это возможно, задачи разными способами, то это может привести и к обратному результату: потере у учащихся интереса к изучаемому, неосознанности выполняемых ими действий, бесполезной трате времени. Перед тем, как предложить учащимся какую-либо задачу, учитель должен досконально изучить ее сам: установить возможные связи с другими задачами, отыскать различные способы решения и выявить целесообразность рассмотрения этих способов для конкретной педагогической ситуации.
На одну задачу, решаемую разными способами, можно смотреть как на своеобразную систему, удовлетворяющую всем предъявляемым к ней требованиям. Такие системы задач в зависимости от типа или этапа урока, специфики рассматриваемых способов решения позволяют добиться различных целей при условии правильной организации работы с ними.
Выделим основные цели решения одной задачи разными способами или методами.
1. Выявление межпредметных связей: алгебра – геометрия, тригонометрия – геометрия и др.
2. Обобщение и систематизация полученных знаний, установление взаимосвязей между различными теоретическими фактами.
3. Выявление сущности определенных методов, их отличительных черт, достоинств и недостатков при применении к конкретным классам задач.
4. Вооружение учащихся различными методами решения задач с целью обретения ими уверенности в своих силах, возможности в случае затруднения перейти к другому приему решения.
5. Демонстрация рациональности, эффективности и изящества одних и нерациональности и порою ошибочности других способов.
6. Показ учащимся одного из приема самоконтроля.
В соответствии с выделенными целями определяются целесообразность и место данных систем задач в учебном процессе, разрабатывается методика их применения и решения.
Рассмотрим на конкретных примерах, как решение одной задачи разными способами или методами может помочь в осуществлении каждой из перечисленных целей.
Выявление межпредметных связей способствует осознанному усвоению учащимися материала, убеждению их в силе математических методов, которые могут быть использованы в разных областях знаний. Поэтому имеет смысл проводить интегрированные уроки, например, алгебры и геометрии.
Пример 1. Вычислите 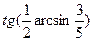
Способ 1 (алгебраический).
Пусть 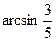
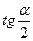
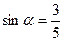
Воспользуемся формулой понижения степени:
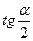
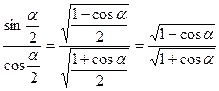
Вычисляя 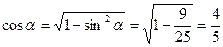
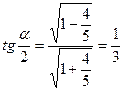
Способ 2 (геометрический).
Воспользуемся понятиями синуса и тангенса острого угла прямоугольного треугольника, теоремой Пифагора и свойством биссектрисы треугольника.
 | В прямоугольном треугольнике АВС ( 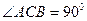 ) ВС=3, АВ=5 и АК – биссектриса угла ВАС. По теореме Пифагора АС=4, а по свойству биссектрисы треугольника СК= ) ВС=3, АВ=5 и АК – биссектриса угла ВАС. По теореме Пифагора АС=4, а по свойству биссектрисы треугольника СК= 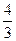 . Получаем, что . Получаем, что 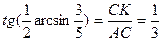 . . |
Важно также сопоставлять арифметический и алгебраический способы решения одной и той же задачи.
Известно, что задачи на концентрацию вызывают значительные затруднения у учащихся. Если же показать им некоторые арифметические способы их решения, то это поможет учащимся осознать основные идеи, используемые при решении задач данного вида.
Пример 2. Имеется лом стали двух сортов, причем первый сорт содержит 10% никеля, а второй 30%. На сколько тонн стали больше нужно взять второго сорта, чем первого, чтобы получить 200 т стали с содержанием никеля 25%?
Способ 1 (алгебраический).
Пусть первого сорта нужно взять х тонн, а второго у тонн. Тогда в стали первого сорта содержится 0,1х тонн никеля, а в стали второго сорта 0,3у тонн никеля. Поскольку в новом сплаве никеля стало 25%, т.е. 0,25·200 = 50 т, то получим следующую систему уравнений:
Из этой системы находим, что х=50, а у=150. Значит, стали второго сорта нужно взять на 100 тонн больше.
Способ 2 (арифметический).
Найдем разность между процентным содержанием никеля в каждом из двух сортов стали и полученном сплаве:
25% – 10% = 15%, 30% – 25% = 5%.
Полученные результаты показывают, что 10%-ного сплава следует взять 5 частей, а 30%-ного – 15 частей. Отсюда легко находится, что нужно взять 50 тонн стали первого сорта и 150 тонн стали второго сорта.
Таким образом, получаем более простой и изящный способ решения задачи, который может применяться при решении подобных задач.
При обобщении и систематизации знаний решение задач разными способами позволяет охватить большой теоретический материал, установить связи между изучаемыми понятиями и фактами.
Пример 3. Найдите радиус окружности, вписанной в равнобедренный треугольник с основанием 10 и боковой стороной 13.
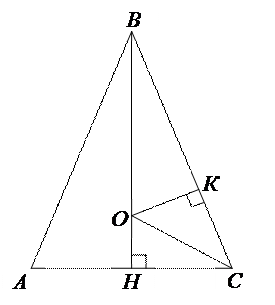 | Способ 1 (использование свойства биссектрисы треугольника). По теореме Пифагора находим, что ВН = 12. Из треугольника ВСН имеем 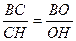 , т.е. , т.е. 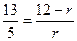 . Отсюда, . Отсюда, 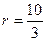 . . |
Способ 2 (использование понятия синуса острого угла прямоугольного треугольника).
Из треугольника ВСН находим 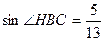
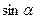
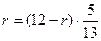
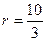
Способ 3 (использование свойства отрезков касательных, проведенных из одной точки к окружности).
Согласно указанному свойству, СН = СК = 5. Значит, ВК = 13 – 5 = 8.
Из треугольника ВКО по теореме Пифагора имеем:
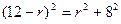
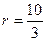
Способ 4 (использование формулы S=pr).
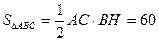
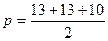
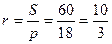
Для достижения третьей цели, т.е. выявления сущности отдельных методов необходима их демонстрация на какой-либо одной задаче. Обычно разные методы демонстрируют на разных задачах, учитывая при этом, какой из них в каждом конкретном случае более эффективен. При таком подходе метод может невольно связаться с самой задачей, а его сущность и значимость остается на втором плане. Когда же разные методы испробованы на одной задаче, то у учащихся появляется возможность оценить их, сравнить, уяснить их особенности. Рассмотрим пример, когда к геометрической задаче применяется векторный, координатный и собственно геометрический методы решения.
Пример 4. Докажите, что в прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине.
Пусть в прямоугольном треугольнике 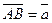 , , 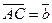 . Тогда медиана . Тогда медиана 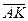 по правилу сложения векторов равна по правилу сложения векторов равна 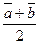 , а гипотенуза , а гипотенуза 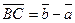 , значит , значит 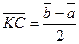 . Необходимо доказать, что длины векторов . Необходимо доказать, что длины векторов 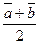 и и  равны, т.е. равны, т.е. 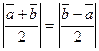 или или 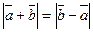 . . |  |
Возведем обе части этого равенства в квадрат: 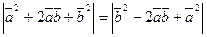

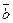
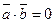
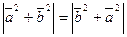
Таким образом, 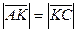
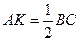
Метод 2 (координатный).
Примем точку А за начало прямоугольной системы координат, а стороны АВ и АС поместим на координатных осях.
Чтобы учащиеся были уверены в своих силах при решении задач и могли переходить от одного приема к другому, необходимо уже при объяснении нового материала рассматривать несколько способов получения верного результата.
Пример 5. Решите уравнение: 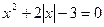
Способ 1 (аналитический).
Данное уравнение равносильно совокупности двух систем:
При решении этой совокупности получаем корни: 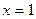
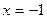
Способ 2 (замена переменной).
Применяя свойство модуля 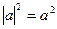
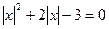
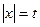
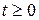
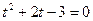
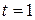
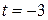
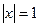
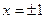
Способ 3 (функциональный).
Функция 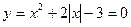

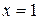
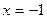
Получаем: 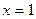
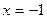
Для достижения пятой цели необходимо подбирать такие задачи, способы решения которых значительно отличаются в плане их эффективности и рациональности, либо задачи, позволяющие выявить некорректность отдельного способа с целью получения важных теоретических выводов.
Пример 6. Решите уравнение: 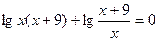
Если предложить учащимся самостоятельно решить данное уравнение, то они могут воспользоваться различными преобразованиями /1/.
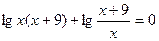

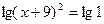
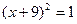
Откуда 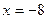

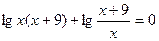
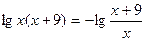
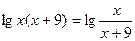
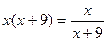
Получаем, что
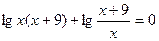
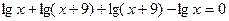
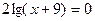
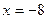
Если в каждом из трех способов решения сделать проверку, то получим, что 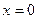
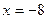

Итак, мы рассмотрели несколько примеров решения задач разными способами. Еще раз обратим внимание на то, что их специфика зависит от целей, поставленных учителем. Теперь обратимся к методике использования таких систем задач на уроках математики. Очевидно, что особенности методики также связаны с целями решения одной задачи разными способами.
Для достижения первой цели, т.е. выявления межпредметных связей, необходимо на первых порах проводить интегрированные уроки. На таких уроках рассматриваются две-три задачи, решаемые разными способами. При этом не следует перед учащимися просто ставить проблему отыскания нескольких способов решения. Нужно четко указать им, что данная задача имеет несколько приемов решения (например, алгебраический и геометрический), а затем подробно остановиться на каждом из них. Если у учащихся возникают трудности, то учитель может наводящими вопросами подвести их к идее решения.
В дальнейшем, когда у учащихся сформируется определенный навык перехода от одной области знаний к другой, можно отказаться от интегрированных уроков. Выявление межпредметных связей следует проводить на обычном уроке, предлагая учащимся самостоятельно найти несколько способов решения одной задачи.
При обобщении и систематизации знаний помощь учителя в отыскании разных способов решения одной задачи должна быть минимальной. Необходимо четко поставить перед учащимися цель: решить задачу двумя, тремя, четырьмя и т.д. способами. Работа может проходить самостоятельно или в группах.
При самостоятельной работе учащимся дается определенное время на решение задачи, после чего, каждый из них сообщает, сколько способов ее решения им было найдено. Затем к доске вызывается любой из учащихся, нашедших только один способ решения задачи, и демонстрирует его. После этого учитель выясняет, кто еще из учащихся «увидел» этот способ, и вызывает к доске следующего учащегося для показа другого способа и т.д.
Примерно так же может быть построена работа в группах. Каждая группа ищет как можно больше способов решения какой-либо задачи, после чего подводятся итоги, и происходит демонстрация способов. В классах с невысоким уровнем подготовки учитель каждой группе может дать задание решить задачу каким-то конкретным способом. Затем представители групп показывают свои способы решения, происходит обсуждение их достоинств и недостатков.
Если поставлена цель ознакомить учащихся с различными методами решения задач, то на первых порах самостоятельность учащихся минимальна. Сначала учитель показывает сущность основных методов, приводит различные примеры. Следующим важным шагом является демонстрация применения различных методов при решении одной и той же задачи. Это позволит учащимся сопоставить изученные методы, провести их сравнительную характеристику, выявить преимущества того или иного методы при решении определенных задач.
Когда учащиеся в достаточной мере овладеют различными методами решения задач, необходимо увеличить степень их самостоятельности. Учащиеся должны при минимальной помощи учителя уметь применять разные методы к решению одной задачи, делать выводы о целесообразности их использования в каждом конкретном случае, грамотно аргументировать свою позицию.
Для достижения четвертой цели учителю необходимо уже при объяснении нового материала вводить различные способы решения одного и того же типа задач (например, аналитический и графический способы решения уравнений с параметром).
В классах с высоким уровнем подготовки учащиеся могут принимать непосредственное участие в поиске таких способов. В классах с невысоким уровнем подготовки учитель сам демонстрирует разные способы решения какого-то вида задач. И в том, и в другом случае необходимо, чтобы учащиеся проанализировали и сопоставили возможные способы, выявили их достоинства и недостатки. Полезно предлагать учащимся задания по предварительному выбору способа решения той или иной задачи в зависимости от ее содержания.
В случае, когда необходимо выявить рациональность и правильность отдельных способов решения задачи, учащимся дается самостоятельное задание по поиску этих способов. Такая работа с одной стороны развивает исследовательские способности учащихся, а с другой – позволяет осознать ошибочность каких-либо действий.
Так при решении логарифмического уравнения (пример 6) и разборе возможных способов используемых преобразований, учитель может организовать дискуссию, в процессе которой поднимаются вопросы о равносильности уравнений и тождественных преобразованиях, нарушающих ОДЗ уравнения. Такой прием будет гораздо более эффективным, чем просто озвучивание учителем этих вопросов. Знания, полученные учащимися при такой работе, станут осознанными и прочными.
Таким образом, методика использования педагогического приема решения одной задачи разными способами в значительной степени зависит от поставленных целей.
Вопросы и задания
1. В чем выражается эффективность использования такого педагогического приема как решение одной задачи разными способами?
2. С какими целями можно связать решение одной задачи разными способами?
3. В чем выражается сущность каждой из этих целей?
4. Каковы характерные особенности методики использования приема решения одной задачи разными способами?
5. В каких случаях учащиеся принимают активное участие в поиске различных способов решения задачи?
6. Решите задачи разными способами:
1) В равнобедренном треугольнике АВС АВ=6, АС=ВС=5. Найдите радиус описанной окружности.
2) В равнобедренном треугольнике АВС АВ=16, АС=ВС=10. Найдите длину медианы АМ.
3) В треугольник АВС вписана окружность, которая точкой касания делит сторону ВС на отрезки, длиной 5 и 9 см. Найдите радиус окружности, если 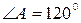
4) Решите уравнение: 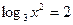
7. Приведите пример решения одной задачи разными способами при выявлении межпредметных связей: алгебра-геометрия, тригонометрия-геометрия.
8. Определите, какой цели соответствует решение уравнения 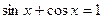
9. Подберите любое уравнение с параметром, которое решается несколькими способами. Опишите методику использования полученной системы задач.
10. Решите задачи к любому параграфу учебника «Геометрия 7-9» под ред. Л.С. Атанасяна и выделите те из них которые решаются разными способами. Рассмотрите эти способы.
Рассмотреть различные способы доказательства свойства биссектрисы треугольника в статье Амелькиной Г. Несколько решений одной задачи. Свойство биссектрисы треугольника. / Газета «Первое сентября. Математика», 2005. – № 1. – с.18-24.
11. Составьте библиографию статей по теме за последние 20 лет в журнале «Математика в школе», газете «Первое сентября. Математика».
Дата добавления: 2014-12-16 ; Просмотров: 14054 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет