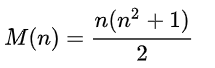Как сделать задание магический квадрат
Как решить магический квадрат: учимся решать одну из древнейших задач
Магический квадрат представляет собой квадратную таблицу с числами, построенную так, что сумма чисел в каждой строке, каждом столбце и в каждой диагонали равна одному и тому же числу (магическая сумма). Магические квадраты бывают разных порядков — порядок квадрата определяет число столбцов/строк. Как рассчитать и решать магические квадраты?
История
Археологи нашли свидетельства того, что волшебные таблицы были известны еще древним грекам и китайцам. «Магическими» эти фигуры назвали арабы, которые наделяли их сверхъестественными защитными свойствами.
В середине XVI в. европейские математики занялись исследованиями загадочных таблиц, положив начало их новой жизни. Они искали общий метод построения магических квадратов и пытались описать все возможные их варианты.
На уроках математики в школе
Решение магических квадратов на уроках математики и внеклассных занятиях вызывает интерес, способствует развитию мышления. Дети учатся планировать и контролировать свою работу. В клетки магических квадратов можно записывать не только числа, но и выражения. Все зависит от изучаемой темы. Задания с магическими квадратами часто дают как дополнительные или олимпиадные уже в начальной школе.
Один из способов решения магического квадрата
Нетрудно решить магический квадрат третьего порядка (у которого по три столбца и строки). Можно воспользоваться тем фактом, что число (выражение), стоящее на пересечении его диагоналей, всегда равно ⅓ волшебной суммы. Отсюда следует алгоритм построения:

Как рассчитать магический квадрат Пифагора самому?
Пифагор — математик, заложивший основы нумерологии. Ученый верил, что миром правят числа. Даже человеческая сущность зависит от них, ведь дата рождения не что иное, как число.
Магический квадрат Пифагора — фигура третьего порядка, клетки которой заполнены числами от 1 до 9. Он делится на 3 уровня: материальный, души и разума.
Цифры даты рождения вписываются в определенном порядке. Полученная комбинация рассказывает о заложенных природой способностях человека.
Материал может быть использован на занятии математического кружка, на внеклассном мероприятии. Цель — развить и расширить познавательный кругозор и логическое мышление.
Решаем магический квадрат Пифагора: пример
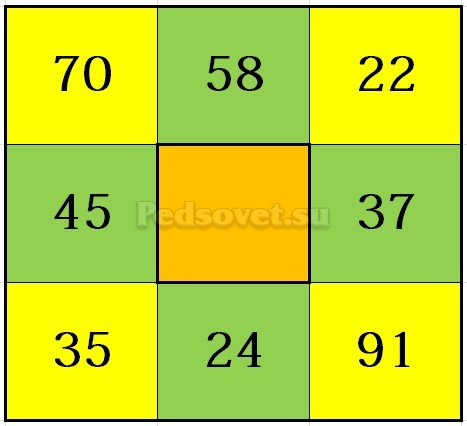
Дата рождения: 17.09.2005 г. Складываем эти цифры, не учитывая нули: 1 + 7 + 9 + 2 + 5 = 24. Аналогично поступаем с цифрами результата: 2 + 4 = 6.
Цифры вписываем в магический квадрат так, чтобы все единицы оказались в первой клеточке, двойки — во второй и так далее. Нули не учитываем.
Клетка 1 – волевые качества, эгоизм.
Очень эгоистичные люди.
Эгоизм — яркая, но не преобладающая черта характера.
Спокойные, покладистые люди.
Сильный, волевой человек.
Люди с замашками диктатора.
Клетка 2 — биоэнергетика.
Воспитанность, природное благородство.
Люди с повышенной чувствительностью к атмосферным изменениям.
Человек с хорошим запасом биоэнергетики.
Клетка 3 — организованность, любовь к точности, конкретности, скрупулезность, скупость.
Чем больше троек, тем сильнее выражены вышеперечисленные качества.
Клетка 4 — здоровье.
Среднее, требуется закаливание.
Очень крепкое здоровье.
Клетка 5 — интуиция, экстрасенсорные способности
Чем больше пятерок, тем более выражена связь с космосом.
Клетка 6 — материализм.
Люди с неординарным воображением, которым необходим физический труд.
Могут посвятить время и творчеству, и точным наукам. Физические нагрузки обязательны.
Заземленные личности, тянущиеся к физическому труду.
Очень много заземленности.
Чем больше семерок, тем талантливее человек.
Клетка 8 — судьба, отношение к обязанностям.
Люди, которые всегда спешат помочь другим.
Признак служения народу.
Клетка 9 — умственные способности
Полное отсутствие девяток означает очень низкий уровень умственной деятельности. Чем больше количество девяток, тем умнее человек.
Задачи на составление магических квадратов часто включаются в сборники нестандартных заданий. Они встречаются на олимпиадах. Увлеченным математикой школьникам будет полезно узнать об этом классе задач.
Об авторе: Филиппова Оксана, учитель математики, физики и информатики.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст
Ошибка в тексте? Мы очень сожалеем,
что допустили ее. Пожалуйста, выделите ее
и нажмите на клавиатуре CTRL + ENTER.
Кстати, такая возможность есть
на всех страницах нашего сайта
2007-2021 «Педагогическое сообщество Екатерины Пашковой — PEDSOVET.SU».
12+ Свидетельство о регистрации СМИ: Эл №ФС77-41726 от 20.08.2010 г. Выдано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций.
Адрес редакции: 603111, г. Нижний Новгород, ул. Раевского 15-45
Адрес учредителя: 603111, г. Нижний Новгород, ул. Раевского 15-45
Учредитель, главный редактор: Пашкова Екатерина Ивановна
Контакты: +7-920-0-777-397, info@pedsovet.su
Домен: https://pedsovet.su/
Копирование материалов сайта строго запрещено, регулярно отслеживается и преследуется по закону.
Отправляя материал на сайт, автор безвозмездно, без требования авторского вознаграждения, передает редакции права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения — в соотв. с ГК РФ. (ст. 1270 и др.). См. также Правила публикации конкретного типа материала. Мнение редакции может не совпадать с точкой зрения авторов.
Для подтверждения подлинности выданных сайтом документов сделайте запрос в редакцию.
Мы используем cookie.
Публикуя материалы на сайте (комментарии, статьи, разработки и др.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьми лицами.
При этом редакция сайта готова оказывать всяческую поддержку как в публикации, так и других вопросах.
Если вы обнаружили, что на нашем сайте незаконно используются материалы, сообщите администратору — материалы будут удалены.
Идеальный магический квадрат. Метод для школьников
На одной из конференций по открытиям в математике я сделал доклад об идеальных магических квадратах. Сокращенно ИМК. После отвечал на вопросы большой аудитории. Их писали на бумажках, передаваемых по рядам кресел. Я зачитывал и, по мере своих знаний, отвечал. После уже, отдыхая в номере гостиницы, снова перечитывал листочки. Одна из записок, которую почему-то не удалось зачитать в зале, оказалась чрезвычайно для меня интересной. Полностью приведу ее текст:
«Скажите пожалуйста, а существует ли самый простой способ построения ИМК, который мог бы осилить школьник младших классов? Например, путём написания натуральных чисел 1,2,3. по определенному несложному правилу. Для простых МК такие способы есть. А для идеальных что-то не встречал.»
Тут было над чем подумать! Не секрет, что школьники с большим удовольствием делают презентации (показом слайдов или видео) по магическим квадратам. Этих презентаций тысячи в инете, но все они однообразные, их материал крайне скуден. Магический квадрат Ло Шу, МК Дюрера, индийский метод для магических квадратов нечетного порядка, шахматный метод для МК двойной четности, МК шестого порядка Ян Хуэя (Китай, 13 век). Хотелось бы выдавать нечто новое, оригинальное, полученное в последние годы. Наука ведь развивается, решаются даже задачи тысячелетия.
Мне лет десять назад удалось создать общий метод построения идеальных магических квадратов при помощи так называемых числовых цепей Александрова. Однако он довольно сложный и не всякий даже старшеклассник его освоит. Хотя я дал в ютубе подробные лекции для студентов, но между студентом и школьником младших классов разница значительная. Как же помочь школьникам? Об этом я постоянно думал на протяжении нескольких месяцев.
Известно, когда всё время занимаешься интересной проблемой и пробуешь множество ходов для её решения, то это решение выявляется как бы случайно. С данной задачей произошло именно так. Мне бы надо было вести дневник всех умственных действий! Получилась бы настоящая детективная история. Такой шанс я к сожалению упустил и остается просто огласить результаты изысканий.
Сочинил детский мнемоничческий стишок, выучив который можно не забыть вышеприведенный способ построения:
Этот метод настолько прост, что его с лёгкостью освоил десятилетний сосед по даче.
Перейдем теперь к построению составных ИМК.
Если мы хотим построить, скажем, ИМК(25), то достаточно продолжить расстановку чисел. Например, на Рис.8 показан второй лист-продолжение. В итоге таких листов должно быть 25 штук. Каждый такой лист обязательно последовательно нумеровать. И уже пронумерованные листы разложить по схеме Рис.6. Получим нужный результат!
Как сделать задание магический квадрат
«Математика-это дверь и ключ к наукам».
Слово « математика» пришло к нам из древнегреческого, означает «учиться», «приобретать знания». И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком». Математика нужна всем! Математика учит нас учиться приобретать знания. А многообразие математических тем, которые можно рассмотреть, завораживает, поэтому выбор темы становится одним из этапов исследования, то есть приобретения новых знаний. Мой выбор пал на «Магические квадраты». Само понятие «магические квадраты» содержит тайну, загадку, а после знакомства с историей и некоторыми свойствами этих квадратов, возникает желание продолжать исследование.
Изучение магических квадратов, их свойств может помочь в развитии:
интереса к предмету математики
А так же решение задач, связанных с магическими квадратами:
предотвращает заболевания, связанные с нарушением работы головного мозга.
Можно ли, используя методы математики, научиться быстро решать судоку, головоломки с числами?
изучение истории появления магических квадратов и способов их заполнения
познакомиться с магическими квадратами
узнать историю возникновения квадратов
изучить правила составления и заполнения магические квадраты
научиться правильно и быстро строить магические квадраты
рассмотреть разновидности магических квадратов
узнать, знакомы ли мои одноклассники с чудесными квадратами
предположить пути дальнейшего исследования
Для заполнения магических квадратов должны существовать специальные способы, которые позволяют сделать это быстро.
изучение специальной литературы;
поиск информации в сети Интернет;
анализ и обобщение.
Глава 1.Теоретическая часть:
1.1. Из истории возникновения магических квадратов.
В 11 в. о магических квадратах узнали в Индии, а затем в Японии.
Из Индии сведения о магических квадратах перешли к арабам. Арабы были знакомы с квадратом третьего порядка в VIII веке, а в XII веке его описал в своих сочинениях Ибн Эзра. Мусульмане очень благоговейно относились к квадратам пятого порядка с цифрой 1 в середине, считая это изображение символом единства Аллаха.
В Западной Европе в средние века магические квадраты были достоянием представителей алхимии и астрологии. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы.
От суеверных представителей древних китайцев, индусов, европейских алхимиков и астрологов эти числовые квадраты и получали своё необычное для математики название – «магические» квадраты. Иногда по отношению к ним употребляется слово «волшебные», но значительно реже, чем «магические». Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты. А любителям математики составление квадратов служило хорошей гимнастикой ума и одно время столь же процветало, как увлечение кроссвордами в наши дни.
В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
Вычисляем «магические квадраты» с помощью GPU
Тема «магических квадратов» достаточно интересна, т.к. с одной стороны, они известны еще с древности, с другой стороны, вычисление «магического квадрата» даже сегодня представляет собой весьма непростую вычислительную задачу. Напомним, чтобы построить «магический квадрат» NxN, нужно вписать числа 1..N*N так, чтобы сумма его горизонталей, вертикалей и диагоналей была равна одному и тому же числу. Если просто перебрать число всех вариантов расстановки цифр для квадрата 4х4, то получим 16! = 20 922 789 888 000 вариантов.
Подумаем, как это можно сделать более эффективно.
Для начала, повторим условие задачи. Нужно расставить числа в квадрате так, чтобы они не повторялись, и сумма горизонталей, вертикалей и диагоналей была равна одному и тому же числу.
Легко доказать, что эта сумма всегда одинакова, и вычисляется по формуле для любого n:
Мы будем рассматривать квадраты 4х4, так что сумма = 34.
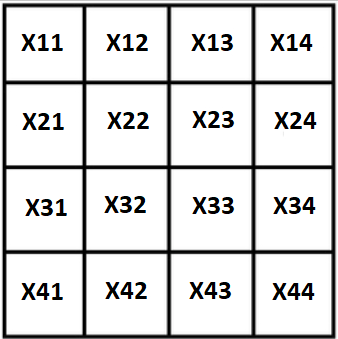
Обозначим все переменные черех X, наш квадрат будет иметь такой вид:
Первое, и очевидное, свойство: т.к. сумма квадрата известна, крайние стоблцы можно выразить через остальные 3:
Таким образом, квадрат 4х4 фактически превращается в квадрат 3х3, что уменьшает число вариантов перебора с 16! до 9!, т.е. в 57млн раз. Зная это, приступаем к написанию кода, посмотрим насколько сложен такой перебор для современных компьютеров.
С++ — однопоточный вариант
Принцип программы весьма прост. Берем множество чисел 1..16 и цикл for по этому множеству, это будет х11. Затем берем второе множество, состоящее из первого за исключением числа x11, и так далее.
Примерный вид программы выглядит так:
Полный текст программы можно найти под спойлером.
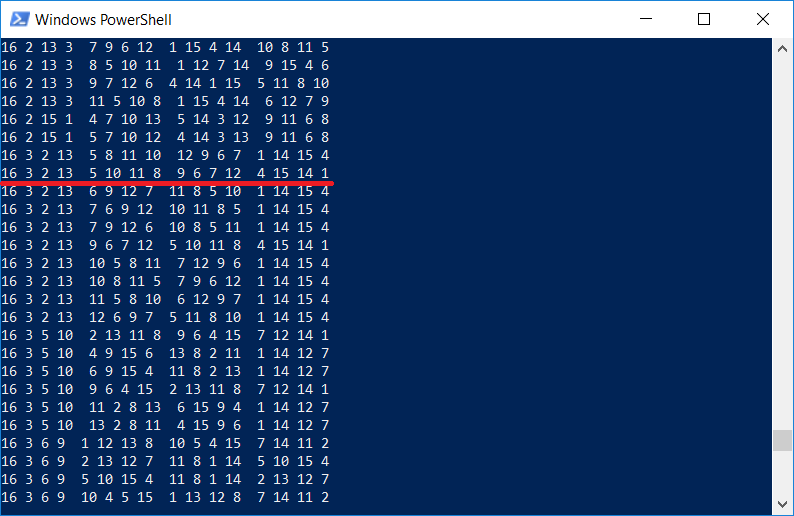
Результат: всего было найдено 7040 вариантов «магических квадратов» 4х4, а время поиска составило 102с.
Кстати интересно проверить, есть ли в списке квадратов тот самый, который изображен на гравюре Дюрера. Разумеется есть, т.к. программа выводит все квадраты размерности 4х4:
Нельзя не отметить, что Дюрер вставил квадрат в изображение не просто так, цифры 1514 также обозначают год создания гравюры.
Как можно видеть, программа работает (отмечаем задачу как verified at 1514 by Albrecht Dürer;), однако время выполнения не так и мало для компьютера с процессором Core i7. Очевидно, что программа выполняется в один поток, и целесообразно задействовать все остальные ядра.
С++ — многопоточный вариант
Переписать программу с использованием потоков в принципе несложно, хотя и немного громоздко. К счастью, есть почти забытый сегодня вариант — использование поддержки OpenMP (Open Multi-Processing). Эта технология существует аж с 1998г, и позволяет директивами процессора указать компилятору, какие части программы выполнять параллельно. Поддержка OpenMP есть и в Visual Studio, так что для превращения программы в многопоточную, достаточно добавить в код лишь одну строку:
Директива #pragma omp parallel for указывает, что следующий цикл for можно выполнять параллельно, а дополнительный параметр squares задает имя переменной, которая будет общей для параллельных потоков (без этого инкремент работает некорректно).
Результат налицо: время выполнения сократилось со 102с до 18с.
Это гораздо лучше — т.к. задача практически идеально распараллеливается (расчеты в каждой ветви не зависят друг от друга), время меньше примерно в число раз, равное количеству ядер процессора. Но увы, принципиально большего из этого кода не получить, хотя какими-то оптимизациями может и можно выиграть несколько процентов. Переходим к более тяжелой артиллерии, расчетам на GPU.
Вычисления с помощью NVIDIA CUDA
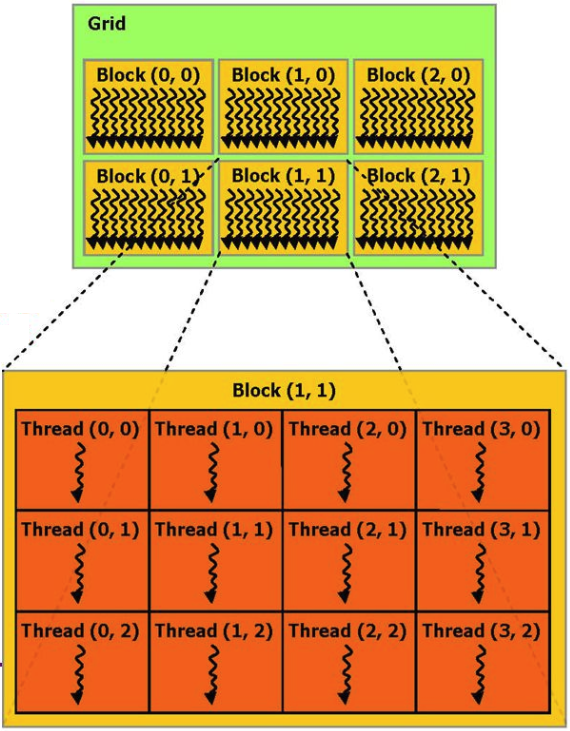
Если не вдаваться в подробности, то процесс вычислений, выполняющийся на видеокарте, можно представить как несколько параллельных аппаратных блоков (blocks), каждый из которых выполняет несколько процессов (threads).
Для примера можно привести пример функции сложения 2х векторов из документации CUDA:
Массивы x и y — общие для всех блоков, а сама функция таким образом выполняется одновременно сразу на нескольких процессорах. Ключ тут в параллелизме — процессоры видеокарты гораздо проще чем обычный CPU, зато их много и они ориентированы именно на обработку числовых данных.
Это то, что нам нужно. Мы имеем матрицу чисел X11, X12. X44. Запустим процесс из 16 блоков, каждый из которых будет выполнять 16 процессов. Номеру блока будет соответствовать число X11, номеру процесса число X12, а сам код будет вычислять все возможные квадраты с для выбранных X11 и X12. Все просто, но здесь есть одна тонкость — данные нужно не только вычислить, но и передать с видеокарты обратно, для этого в нулевом элементе массива будем хранить число найденных квадратов.
Основной код получается весьма простым:
Мы выделяем блок памяти на видеокарте с помощью cudaMalloc, запускаем функцию squares, указав ей 2 параметра 16,16 (число блоков и число потоков), соответствующие перебираемым числам 1..16, затем копируем данные обратно через cudaMemcpy.
Сама функция squares по сути повторяет код из предыдущей части, с той разницей, что приращение количества найденных квадратов делается с помощью atomicAdd — это гарантирует что переменная будет корректно изменяться при одновременных обращениях.
Результат не требует комментариев — время выполнения составило 2.7с, что примерно в 30 раз лучше изначального однопоточного варианта:
Как подсказали в комментариях, можно задействовать еще больше аппаратных блоков видеокарты, так что был испробован вариант из 256 блоков. Изменение кода минимально:
Это сократило время еще в 2 раза, до 1.2с. Далее, на каждом блоке можно запустить 16 процессов, что дает наилучшее время 0.44с.
Скорее всего, это далеко не идеал, например можно запустить еще больше блоков на GPU, но это сделает код более запутанным и сложным для понимания. И разумеется, расчеты даются не «бесплатно» — при загруженном GPU интерфейс Windows начинает заметно подтормаживать, а энергопотребление компьютера увеличивается практически в 2 раза, с 65 до 130Вт.
Правка: как подсказал в комментариях пользователь Bodigrim, для квадрата 4х4 выполняется еще одно равенство: сумма 4х «внутренних» ячеек равна сумме «внешних», она же равна S.
X22 + X23 + X32 + X33 = X11 + X41 + X14 + X44 = S
Это позволит еще ускорить алгоритм, выразив одни переменные через другие и убрав еще 1-2 вложенных цикла, обновленный вариант кода можно найти в комментарии ниже.
Заключение
Задача нахождения «магических квадратов» оказалась технически весьма интересной, и в то же время непростой. Даже с вычислениями на GPU поиск всех квадратов 5х5 может занять несколько часов, а оптимизацию для поиска магических квадратов размерности 7х7 и выше, еще предстоит сделать.
Математически и алгоритмически, тоже есть несколько нерешенных моментов: