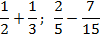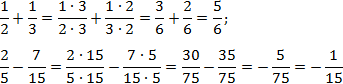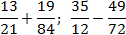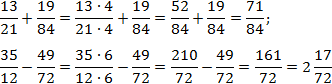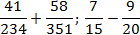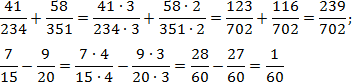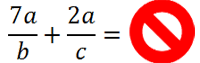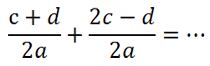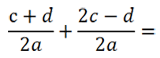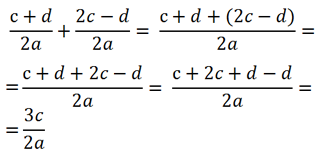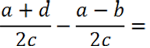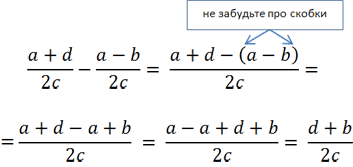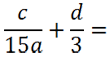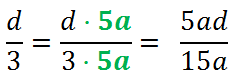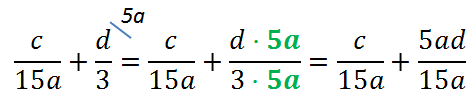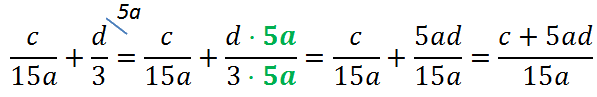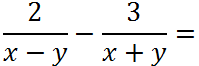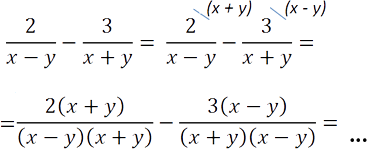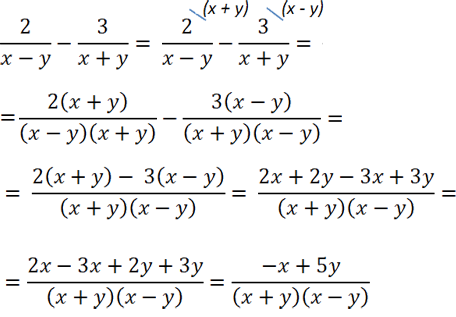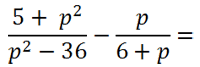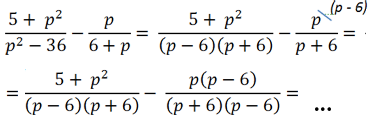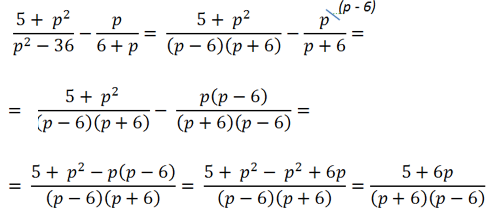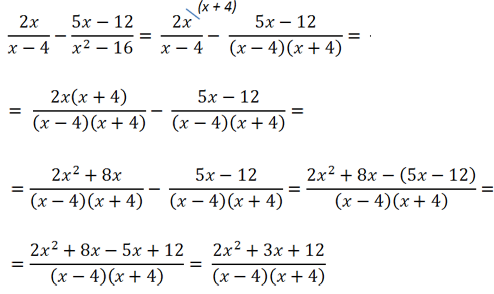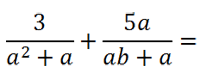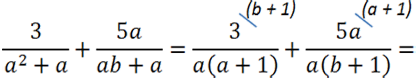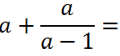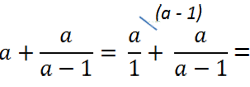Как сделать знаменатель одинаковым
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
Задача. Найдите значения выражений:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Приведение дробей к общему знаменателю
Общий знаменатель обыкновенных дробей
Любые дроби с разными знаменателями в математике можно привести к одному и тому же общему знаменателю — заменить на равные им дроби с одинаковым знаменателем.
Есть два вида знаменателей:
Общий знаменатель — это число или выражение, которое является знаменателем для двух и более обыкновенных дробей.
Наименьший общий знаменатель — наименьшее общее кратное знаменателей данных дробей.
Производить данную операцию необходимо в ряде случаев.
Как привести дроби к общему знаменателю, алгоритм
Чтобы осуществить операцию приведения, необходимо применить основное свойство дробей: если числитель и знаменатель дроби умножить на одно и то же число, отличное от нуля, дробь не изменится. То есть если подобрать правильные множители, то можно привести знаменатели к одному и тому же числу. Искомые множители называют дополнительными.
Это объяснение лежит в основе общего правила приведения дробей.
Существует несколько способов привести дроби к общему или наименьшему общему знаменателю.
Умножение «крест-накрест»
Самый простой способ — умножение «крест-накрест». Применяется следующий пошаговый алгоритм:
Недостаток этого метода — в размерах вычислений. При умножении могут получиться большие числа, которыми тяжело оперировать.
Метод общих делителей
Иногда один из знаменателей дроби уже делится на другой без остатка. В таком случае нет нужды перемножать их, количество действий сокращается.
Этот метод хорош тем, что является более кратким вариантом умножения «крест-накрест». При этом его невозможно использовать при решении примеров, в которых числа в знаменателях не делятся друг на друга.
Метод наименьшего общего кратного
Суть приведения заключается в том, чтобы найти такое число, которое делится на каждый из знаменателей. К этому числу и необходимо привести знаменатели обеих дробей.
Наименьшее общее кратное (НОК) — это наименьшее число, на которое делится каждый из знаменателей. Обозначается он как НОК (a; b).
НОК (3; 4) = 12; НОК (8; 12) = 24.
Иногда найти НОК можно «на глаз», не выполняя дополнительных расчетов. К примеру, НОК (6; 9) = 18. Однако иногда на это может понадобиться больше времени. Описание примера таких вычислений приведено в примерах решения задач ниже.
Таким образом, основное преимущество это метода заключается в краткости вычислений. При этом его недостатком является сложность нахождения НОК в некоторых случаях.
Примеры задач с подробным решением
Задача
Решение
Для начала применим метод «крест-накрест». Тогда:
Получившуюся дробь можно сократить на 5:
Однако решение можно сократить, применив метод общих делителей. 15 делится на 5 без остатка. При таком делении дополнительным множителем для первой дроби будет число 3:
Задача
Решение
Решить эту задачу методом общих делителей невозможно, ведь 20 не делится без остатка на 15. При этом оба числа являются большими:
Вычисление методом «крест-накрест» будет слишком большим.
Оптимальным вариантом решения является метод наименьшего общего кратного.
\(НОК (15; 20) = 5\cdot3\cdot4=60\)
При делении 60 на знаменатели обеих дробей получаются дополнительные множители 4 и 3. Используем их для вычислений:
Получившуюся дробь можно сократить на 30:
Работы любой сложности
Квалифицированная помощь от опытных авторов
Как складывать дроби
Простое руководство для тех, кому нужно вспомнить школьную программу или помочь ребёнку.
Какие бывают дроби
Дробь — это число, которое состоит Дробь из одной или из нескольких равных частей единицы. Говоря упрощённо, это число обозначает часть чего‑либо, например один кусок торта, или целое с несколькими дополнительными частями, например один целый торт и ещё три куска другого.
Обыкновенные дроби состоят из числителя (вверху) и знаменателя (внизу), разделённых горизонтальной или косой чертой. Знаменатель отражает то, на сколько частей можно разделить наш условный торт, а числитель — сколько из них в наличии: 1 /2, 3 /4, 9 /10.
Обыкновенные дроби бывают правильные и неправильные. У правильных числитель меньше знаменателя ( 5 /8, 7 /15), а у неправильных наоборот — больше ( 8 /5, 15 /7). Из неправильной дроби можно выделить целую и дробную части: 1 3 /5, 2 1 /7. Получившееся число будет называться смешанной дробью.
Бывают ещё десятичные дроби. У них в знаменателе стоит степень числа 10, и они записываются по‑другому — через запятую: 0,5, 0,98. Хотя десятичные дроби можно представить и в виде обыкновенных: 5 /10, 98 /100.
Как складывать дроби
Обыкновенные с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, просто суммируйте их числители, а знаменатели оставьте без изменений. Например: 1 /5 + 2 /5 = 3 /5; 9 /6 + 10 /6 = 19 /6 = 3 1 /6.
Обыкновенные с разными знаменателями
Сначала нужно привести дроби к общему знаменателю. Для этого найдите наименьшее число, которое без остатка делится на оба ваших знаменателя. Например, для дробей 5 /6 и 4 /9 это число 18.
Затем разделите его на ваши знаменатели — и вы получите так называемый дополнительный множитель (18 : 6 = 3, 18 : 9 = 2). Это число, на которое нужно умножить обе части дроби, чтобы привести её к новому знаменателю. То есть: 5 x 3 /6 x 3 + 4 x 2 /9 x 2 = 15 /18 + 8 /18.
Остаётся только повторить процесс из предыдущего пункта, сложив числители. В нашем примере получится 23 /18, или 1 5 /18, если выделить целую часть.
Смешанные дроби
Складывать такие дроби можно несколькими способами. Самый простой — суммировать целые и дробные части отдельно. Например, вам нужно сосчитать, сколько будет 3 1 /5 + 4 2 /3. Сначала складываем 3 + 4 и получаем 7. Потом переходим к дробным частям: 1 /5 + 2 /3 = 1 x 3 /5 x 3 + 2 x 5 /3 x 5 = 3 /15 + 10 /15 = 13 /15. А вместе — 7 13 /15.
Если при сложении дробных частей получается неправильная дробь, из неё тоже нужно выделить целое и добавить к полученной ранее целой части.
Десятичные дроби
Первым делом нужно уравнять количество цифр после запятой. Например, вы хотите сложить числа 33,142 и 5,6. Добавьте два нуля ко второй дроби — 5,600. Теперь сложите между собой числа до запятой (33 + 5) и после (142 + 600). Получится 38,742.
Если вы ещё не очень хорошо освоили работу с десятичными дробями, суммируйте их столбиком, как обычные числа. Следите за тем, чтобы запятая была под запятой. Такой метод сложения облегчит вам подсчёты в том случае, когда после запятой появляется «лишняя» цифра.
Например, нужно найти сумму чисел 1,742 и 5,6. Вы уже знаете, что 1 + 5 = 6, а 742 + 600 = 1 342, но в столбике вы сразу увидите, что единицу из 1 342 нужно перенести, добавить к целой части. В итоге получится 7,342.
Правила сложения и вычитания алгебраических дробей
Сложение и вычитание алгебраических дробей
Дробь — это доля числа. Она представлена в виде \frac mn, где m и n — любые натуральные числа. В данной записи m является числителем, а n — знаменателем.
Для того чтобы производить операции с дробями, необходимо знать их основное свойство. Оно состоит в следующем: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Одно и то же количество можно выразить разными эквивалентными дробями.
Если числитель и знаменатель дроби \(\frac12\) умножить на 2, получится равная ей дробь \(\frac24.\)
Основные правила, операции без преобразования
Главное правило сложения и вычитания дробей заключается в том, что операции можно проводить только между дробями с одинаковым знаменателем.
Если знаменатели двух дробей одинаковы, то можно сразу сложить или вычесть, в зависимости от задачи, числители этих дробей, а знаменатель оставить прежним. Если это возможно, дробь нужно сократить.
Общее правило сложения и вычитания дробей с одинаковым знаменателем выглядит следующим образом:
где a, b и с — натуральные числа, \(b\neq0.\)
Если знаменатели разные, дроби необходимо заменить на эквивалентные с одинаковым знаменателем. Выполнить операцию необходимо уже с этими новыми дробями. Распространяется это как на положительные, так и на отрицательные дроби.
Сложение и вычитание алгебраических дробей
Приведение алгебраических дробей к общему знаменателю
Для каждой дроби существует бесконечное количество эквивалентных дробей. Это значит, что обязательно есть знаменатель, являющийся одинаковым для двух или более дробей, с которыми производится действие. Такой знаменатель называют общим.
Чтобы упростить вычисления, обычно используют метод наименьшего общего кратного.
Наименьшее общее кратное (НОК) — это такое наименьшее натуральное число, которое делится одновременно на оба числа. В данном случае это числа, стоящие в знаменателях двух дробей.
Для чисел 2 и 3 произведение и НОК = 6; для чисел 5 и 10 произведение равно 50, а НОК = 10; произведение чисел 4 и 6 равно 24, а их НОК = 12.
Как видно из последних двух примеров, НОК зачастую меньше, чем производное двух данных чисел. Благодаря НОК можно значительно сократить запись решения, поскольку отпадает нужда в ненужном сокращении дробей.
Чтобы найти НОК, необходимо разложить знаменатели обеих дробей на простые множители, а затем выбрать в разложении наименьшего знаменателя множители, не вошедшие в разложение большего знаменателя, и добавить их туда. После чего перемножить все полученные множители.
Найдем НОК чисел 12 и 18.
В разложение наименьшего знаменателя 12 вошли множители 3, 2 и 2. А в разложении наибольшего знаменателя 18 множитель 2 встречается только один раз, в нем не хватает еще одного множителя 2. Поэтому мы добавляем его к множителям числа 18. Получаем:
Чтобы привести дроби к общему знаменателю, необходимо найти не только НОК, но и дополнительный множитель. Это такой множитель, на который необходимо умножить каждую из дробей. Для этого необходимо поделить НОК на знаменатель каждой дроби.
Найдем дополнительный множитель для дробей \(\frac1<12>\) и \(\frac5<18>.\)
НОК для этих дробей уже известно и равно 36. Тогда:
Следовательно, дополнительный множитель для первой дроби равен 3, а для второй – 2.
Затем каждую дробь необходимо умножить на дополнительный множитель и произвести действия с полученными дробями с одинаковыми знаменателями.
Найдем значения выражений \( \frac1<12>+\frac5<18>\) и \(\frac5<18>-\frac1<12>.\)
Таким образом, можно сформулировать алгоритм сложения и вычитания алгебраических дробей с разными знаменателями.
С помощью формул сокращенного умножения
Иногда в знаменателе находится не простое число, а выражение, так что найти НОК не удается. В таких случаях стоит присмотреться к выражению в знаменателе: возможно, там будет формула сокращенного умножения. К таким формулам относят:
С вынесением общего множителя за скобки
При нахождении общего знаменателя может понадобиться разложить исходный сложный знаменатель на множители, чтобы упростить его.
С одночленом или числом
Если необходимо сложить (вычесть) дробь и натуральное число, необходимо представить это число в виде дроби с тем же знаменателем. Результатом вычисления может получиться неправильная дробь — в таком случае необходимо преобразовать ее в смешанное число.
Если число не целое, а смешанное, то работать нужно отдельно с целыми и дробными частями.
В случае с одночленами, то есть выражениями с одной переменной, действия производятся так же, как и с целыми числами. Одночлен необходимо представить в виде дроби.
Сложение и вычитание алгебраических дробей
Алгебраические дроби складывают и вычитают по правилам сложения и вычитания обыкновенных дробей.
Сложение алгебраических дробей
Складывать можно только дроби с одинаковыми знаменателями!
Нельзя складывать дроби без преобразований
Можно складывать дроби
При сложении алгебраических дробей с одинаковыми знаменателями:
Рассмотрим пример сложения алгебраических дробей.
Так как знаменатель у обеих дробей « 2а », значит, дроби можно сложить.
Сложим числитель первой дроби с числителем второй дроби, а знаменатель оставим прежним. При сложении дробей в полученном числителе приведем подобные.
Вычитание алгебраических дробей
Вычитать можно только дроби с одинаковыми знаменателями!
При вычитании алгебраических дробей с одинаковыми знаменателями:
Обязательно заключите в скобки весь числитель вычитаемой дроби.
Иначе вы сделаете ошибку в знаках при раскрытии скобок вычитаемой дроби.
Рассмотрим пример вычитания алгебраических дробей.
Так как у обеих алгебраических дробей знаменатель « 2с », значит, эти дроби можно вычитать.
Вычтем из числителя первой дроби « (a + d) » числитель второй дроби « (a − b) ». Не забудем заключить числитель вычитаемой дроби в скобки. При раскрытии скобок используем правило раскрытия скобок.
Приведение алгебраических дробей к общему знаменателю
Рассмотрим другой пример. Требуется сложить алгебраические дроби.
В таком виде сложить дроби нельзя, так как у них разные знаменатели.
Прежде чем складывать алгебраические дроби их необходимо привести к общему знаменателю.
В итоге мы должны получить многочлен, который без остатка разделится на каждый прежний знаменатель дробей.
Чтобы привести алгебраические дроби к общему знаменателю необходимо сделать следующее.
Вернемся к нашему примеру.
Рассмотрим знаменатели « 15a » и « 3 » обеих дробей и найдем для них общий знаменатель.
Рассмотрим первую дробь. В этой дроби и так знаменатель « 15a », значит, ее не требуется ни на что умножать.
Рассмотрим вторую дробь. Зададим вопрос: «На что нужно умножить « 3 », чтобы получить « 15a »?» Ответ — на « 5a ».
Для этого держим в уме общий знаменатель. Над каждой дробью сверху «в домике» пишем, на что умножаем каждую из дробей.
Теперь, когда у дробей одинаковые знаменатели, дроби можно сложить.
Рассмотрим пример вычитания дробей с разными знаменателями.
В таком виде вычитать дроби нельзя, так как у них разные знаменатели. Чтобы вычесть дроби, необходимо привести их к общему знаменателю.
Рассмотрим знаменатели « (x − y) » и « (x + y) » обеих дробей и найдем для них общий знаменатель.
Многочлены необходимо рассматривать целиком! Для удобства заключайте целый многочлен в скобки.
У нас есть два различных многочлена в знаменателях « (x − y) » и « (x + y) ». Их произведение будет общим знаменателем, т.е. « (x − y)(x + y) » — общий знаменатель.
Теперь дроби можно вычитать, т.к. у них одинаковый знаменатель.
Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения
В некоторых примерах, чтобы привести алгебраические дроби к общему знаменателю, нужно использовать формулы сокращенного умножения.
Рассмотрим пример сложения алгебраических дробей, где нам потребуется использовать формулу разности квадратов.
В первой алгебраической дроби знаменатель « (p 2 − 36) ». Очевидно, что к нему можно применить формулу разности квадратов.
После разложения многочлена « (p 2 − 36) » на произведение многочленов
« (p + 6)(p − 6) » видно, что в дробях повторяется многочлен « (p + 6) ». Значит, общим знаменателем дробей будет произведение многочленов « (p + 6)(p − 6) ».
Прежде чем приводить многочлены к общему знаменателю, попытайтесь использовать формулы сокращённого умножения или вынесение общего множителя за скобки.
Примеры сложения и вычитания дробей с разными знаменателями с использованием формул сокращенного умножения.
Сложение и вычитание алгебраических дробей с вынесением общего множителя за скобки
На первый взгляд одинаковых многочленов в обеих дробях нет.
Вынесем общий множитель « а » за скобки в обоих знаменателях.
После вынесения общего множителя « а » за скобки, в обоих знаменателях появился одинаковый одночлен « а ». Значит, общий знаменатель для обеих дробей будет выглядеть так: « а(а + 1)(b + 1) ».
Сложение алгебраической дроби с одночленом или числом
Рассмотрим пример. Требуется сложить алгебраическую дробь с одночленом (буквой).
Чтобы сложить одночлен или число с алгебраической дробью, нужно представить одночлен в виде дроби со знаменателем « 1 ».
Представим одночлен « а » как алгебраическую дробь со знаменателем « 1 ».
Подобное действие можно сделать, так как при делении на единицу получается тот же самый одночлен.
Теперь приведем алгебраические дроби к общему знаменателю « (а − 1) » и решим пример.