Как сделать зонную пластинку

Учебники

Журнал «Квант»

Общие

Насретдинов А. Опыты с пластинкой Френеля //Квант. — 1992. — № 4. — С. 47-49.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Из школьного курса физики вы знаете, что можно фокусировать свет при помощи линзы. Но, конечно, линза — не единственная такая возможность. Сегодня мы поговорим об одном достаточно интересном приборе — зонной пластинке Френеля (ее иногда называют просто зонной пластинкой или пластинкой Френеля), с помощью которой тоже можно фокусировать свет.

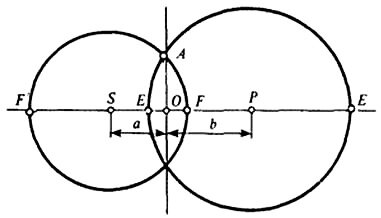
Что же представляет собой пластинка Френеля? Для того чтобы понять это, рассмотрим следующий пример. Пусть между точечным источником монохроматического света S и точкой наблюдения Р поставлен непрозрачный экран, плоскость которого перпендикулярна оси SP (рис. 1). Найдем на экране геометрическое место точек, сумма расстояний от каждой из которых до точек S и Р отличается от расстояния SP на целое число длин полуволн. Если А — одна из искомых точек, то

где m — целое число.

Из точек S и Р как из центров опишем окружности, проходящие через точку А. Из рисунка 1 видно, что

SA + AP = SP + EF,\) где \(

EF = EO + OF = \frac 12 \left( \frac 1a + \frac 1b \right) OA^2.\)

Но, с другой стороны, \(

EF = m \frac<\lambda><2>\), поэтому можно написать, что

OA = \sqrt<\frac m \lambda> = \operatorname \sqrt m, \qquad (1)\)

т. е. в плоскости отверстия искомым геометрическим местом точек является система концентрических окружностей с центром в точке О. Радиус первой окружности (для m = 1) равен

Радиусы последующих окружностей R_m увеличиваются в \(

Таким образом, мы разбили плоскость экрана на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки Р отличаются на \(

Что произойдет, если в непрозрачном экране сделать отверстие радиусом первой зоны Френеля? Согласно принципу Гюйгенса — Френеля, когда волновой фронт от источника света достигнет краев отверстия, все точки волнового фронта, ограниченного отверстием, можно рассматривать как вторичные источники сферических волн. Так как разность хода между этими волнами в точке Р не превышает \(

\frac<\lambda><2>\), эти волны, интерферируя, усилят друг друга. Расчет показывает, что в сравнении со случаем отсутствия экрана интенсивность света в точке Р возрастает в четыре раза! Это означает, что свет как бы сфокусировался в точке Р.

Если на пути световой волны поставить непрозрачную пластинку, которая закрывает все четные (или все нечетные) зоны, то интенсивность света в точке Р резко возрастает. Это происходит вследствие того, что колебания от открытых зон приходят в точку Р синфазно и, интерферируя, усиливают друг друга. Такая пластинка и является зонной пластинкой Френеля. На рисунке 2, например, показана зонная пластинка, закрывающая нечетные зоны.

Можно сказать, что усиление интенсивности света зонной пластинкой аналогично фокусирующему действию линзы. Более того, расстояния от пластинки до источника S и «изображения» Р связаны тем же соотношением, что и соответствующие величины для линзы. Это сразу станет видно, если мы перепишем выражение (1) в виде

\frac 1a + \frac 1b = \frac 1f,\)

где «фокусное расстояние» определяется формулой

Так как фокусное расстояние пластинки Френеля зависит от длины волны, определив его и зная размеры самой пластинки, вы легко сможете определить длину волны источника света.

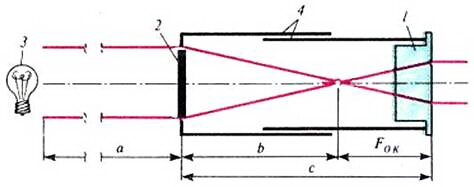
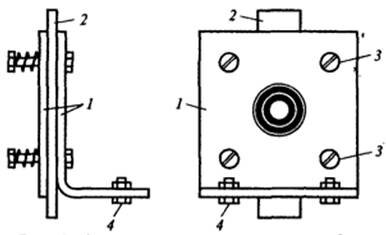
Практически фокусное расстояние пластинки Френеля можно определить с помощью приспособления, изображенного на рисунке 3. Вам понадобятся: короткофокусный окуляр (от подзорной трубы, микроскопа и т. д.), кусок ватмана или жести для изготовления телескопической системы из трубок 4. Также нужно изготовить держатель для пленки (пластинок Френеля). Его возможная конструкция показана на рисунке 4.

Вставьте в держатель один из негативов. Меняя длину системы трубок, добейтесь наилучшего изображения источника света. Измерьте значение c. Считая лампочку удаленным источником (\(

a \gg b\)), для фокусного расстояния пластинки Френеля можно написать следующие соотношения:

\frac 1f = \frac 1a + \frac 1b,\) где \(

Таким образом, измерив значение с и зная фокусное расстояние окуляра F_ok, вы получите фокусное расстояние пластинки Френеля.

Теперь осталось определить радиус первой зоны. К сожалению, измерить его с хорошей точностью непосредственно на негативе не удастся, поэтому пересчитайте его значение, измерив радиус внешней зоны и воспользовавшись формулой (1).

Итак, зная все необходимые величины, по формуле (2) вы найдете длину волны источника света. Проведя же аналогичные измерения для нескольких пластинок, можно более точно определить значение длины волны.

Рекомендуемые размеры для проведения экспериментов:

Предлагаемый опыт можно существенно «украсить», поставив различные светофильтры или изменяя температуру накала нити, варьируя тем самым длину волны излучаемого лампочкой света. А воспользовавшись негативом, на котором зонная пластинка снята под некоторым углом к нормали, вы сможете наблюдать очень красивые картинки.

Источник

Зонные пластинки. Фокусировка

Открывая постепенно диафрагму, можно наблюдать в точке P рост результирующего колебания. Этот рост закончится, когда диафрагма целиком откроет первую зону Френеля (E₁).

При дальнейшем увеличении диафрагмы начнут открываться области второй зоны. Результирующая амплитуда в точке наблюдения начнёт уменьшаться. Она станет почти нулевой, когда окажутся открытыми первые две зоны Френеля.

Затем вновь начнётся рост амплитуды: открывается третья зона. Открытие четвёртой зоны ознаменуется снижением амплитуды. Таким образом, каждая чётная зона «гасит» волну от предыдущей нечётной.

На рисунке 7.12 приведена векторная диаграмма для случая, когда чётные зоны отсутствуют. Как это можно сделать? Для этого надо изготовить такую преграду-маску, которая закрывала бы все чётные зоны но оставалась бы прозрачной для нечётных (Пример такой маски – на рис. 7.13).

Амплитуда колебаний в точке P в этом случае резко возрастёт (рис. 7.12). Это результат того, что удалось исключить гасящее влияние чётных зон.

Можно создать преграду, прозрачную для всех зон, но такой формы, чтобы оптический ход волны от каждой чётной зоны оказался бы на λ больше оптического хода волны от предыдущей нечётной зоны (рис. 7.14).

В этом случае чётные зоны не исключаются. Их фаза увеличивается на π, и они создают в точке наблюдения колебания, синфазные с колебаниями соседних нечётных зон.

Соответствующая векторная диаграмма представлена на рис. 7.15а.

Ну и, наконец, можно ведь создать зонную пластинку более тонкой структуры. Пластинку, влияющую не на целые зоны, а только на подзоны. Это означает, что следует ступенчатую зонную пластинку заменить собирающей линзой. Эффект ее действия представлен на векторной диаграмме 7.15в.

.

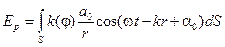
Лекция 8 «Дифракция волн»

1. Дифракция Фраунгофера от длинной щели

2. Интенсивность дифракционной картины

3. Критерий типа дифракции

На прошлой лекции обсуждался принцип Гюйгенса-Френеля. Был записан интеграл Френеля:

(8.1)

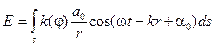
Теперь обратимся к дифракции в параллельных пучках – к дифракции Фраунгофера.

Дата добавления: 2014-01-15 ; Просмотров: 344 ; Нарушение авторских прав?

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Зонная пластинка Френеля

Интенсивность света в точке Р можно многократно усилить, прикрыв все четные или нечетные зоны Френеля. Такую операцию можно сделать с помощью амплитудной зонной пластинки.

Зонная пластинка работает для монохроматического света как линза с фокусным расстоянием :

.

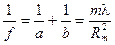
Рис. 10.5. Кольцевые зоны амплитудной зонной пластинки Френеля.

В отличие от линзы зонная пластинка имеет множество фокусов, находящихся на её оптической оси.

Более эффективной по сравнению с амплитудной, показанной на рис. 10.5, является фазовая зонная пластинка. В отличие от амплитудной, фазовая пластинка содержит такие же кольцевые зоны, но из прозрачного материала с оптической толщиной в половину длины волны, нанесенные на стеклянную подложку. Тем самым все зоны четные и нечётные дают вклад в освещенность центрального пятна, поэтому светосила фазовой пластинки в два раза больше, чем у амплитудной.

Амплитудную фазовую пластинку можно изготовить методом фотолитографии путем нанесения металлического покрытия в виде колец, как показано на рис.10.5. Фазовую зонную пластинку изготавливают также методом фотолитографии путем травления прозрачного слоя с оптической толщиной в половину длины волны, нанесенного на стеклянную подложку.

Киноформы – зонные пластинки сложной формы для фокусировки и создания заданного распределения интенсивности в фокальной плоскости для излучения лазера. Требуемую форму зон рассчитывают с помощью компьютера и изготавливают на фотолитографическом оборудовании, применяемом в технологии микроэлектроники.

щенность, создаваемая первой зоной, как уже упоминалась, больше, чем прямое освещение экрана источником света. То есть отверстие малого размера работает как фокусирующая линза.

Рис. 10.6. Камера-обскура создает перевернутое изображение предметов, находящихся перед ней, на задней стенке ящика.

На задней стенке ящика возникает перевернутое изображение объекта АВ, который можно считать состоящим из множества светящихся точек.

Камеру-обскуру применяли в качестве фотоаппарата при получении первых фотографий. Недостаток камеры-обскуры – низкая светосила. Через отверстие камеры-обскуры проходит слишком мало света, рассеянного объектом и создающим его изображение. Поэтому для получения фотографического портрета человеку приходилось неподвижно сидеть перед камерой в течение нескольких минут.

Дата добавления: 2014-01-13 ; Просмотров: 2269 ; Нарушение авторских прав?

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Зонная пластинка Френеля

Зонная пластинка — плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями, радиус которых совпадает с радиусами зон Френеля. Зонная пластинка «выключает» чётные либо нечётные зоны Френеля, чем исключает взаимную интерференцию (погашение) от соседних зон, что приводит к увеличению освещённости точки наблюдения. Таким образом, зонная пластинка действует как собирающая линза.

Также зонная пластинка представляет собой простейшую голограмму — голограмму точки.

Содержание

Принцип действия

Согласно принципу Гюйгенса-Френеля световое поле в некоторой точке пространства является результатом интерференции вторичных источников. Френель предложил оригинальный и чрезвычайно наглядный метод группировки вторичных источников. Этот метод позволяет приближенным способом рассчитывать дифракционные картины, и носит название метода зон Френеля.

Зоны Френеля вводятся следующим образом. Рассмотрим распространение световой волны из точки L в точку наблюдения P. Сферический волновой фронт, исходящий из точки L разобьем концентрическими сферами с центром в точке P и с радиусами z1 + λ/2; z1 + 2 λ/2; z1 + 3 λ/2…

Полученные кольцевые зоны и носят название зон Френеля.

Смысл разбиения поверхности на зоны Френеля состоит в том, что разность фаз элементарных вторичных волн, приходящих в точку наблюдения от данной зоны, не превышает π. Сложение таких волн приводит к их взаимному усилению. Поэтому каждую зону Френеля можно рассматривать как источник вторичных волн, имеющих определенную фазу. Две соседние зоны Френеля действуют как источники, колеблющиеся в противофазе, т.е вторичные волны, распространяющиеся из соседних зон в точке наблюдения будут гасить друг друга. Чтобы найти освещенность в точке наблюдения P нужно просуммировать напряженности электрических полей от всех вторичных источников, приходящих в данную точку. Результат сложения волн зависит от амплитуды и разности фаз. Так как разность фаз между соседними зонами равна P, то можно перейти к суммированию амплитуд.

Амплитуда вторичной сферической волны пропорциональна площади элементарного участка, испускающего эту волну (т.е пропорциональна площади зоны Френеля). Кроме того, она убывает с увеличением расстояния z1 от источника вторичной волны до точки наблюдения по закону 1 / z1 и с ростом угла φ между нормалью к элементарному участку, испускающего волну, и направлением распространения волны.

Можно показать, что площади зон Френеля примерно одинаковы и равны:

, где Sn — площадь n-ой зоны Френеля, z0 — радиус сферы.

Расстояние z1n от зоны до точки наблюдения медленно растет по линейному закону: z1n = z1 + n λ / 2, где n — номер зоны.

Угол φ также увеличивается при увеличении номера зоны Френеля. Следовательно, амплитуды вторичных волн убывают. Таким образом, можно записать A1 > A2 > A3 > … > An-1 > An > An+1 > …, где An — амплитуда вторичной волны, испущенной n-ой зоной. Амплитуда результирующего светового колебания в точке наблюдения P будет определяться вкладом всех зон. При этом, волна из второй зоны Френеля будет гасить волну из первой зоны (так как они придут в точку P в противофазе), волна из третьей зоны будет усиливать первую волну (так как между ними разность фаз равна нулю), четвертая волна ослабит первую и так далее. Это значит, что при суммировании необходимо учесть, что все четные зоны дадут вклад в результирующую амплитуду одного знака, а все нечетные зоны — противоположного знака. Таким образом, суммарная амплитуда в точке наблюдения равна: A = A1 — A2 + A3 — A4 + …

Это выражение можно переписать в виде:

Тогда выражения, заключенные в круглые скобки будут равны нулю, и амплитуда А в точке наблюдения будет равна: А = А1/2. То есть амплитуда, создаваемая в некоторой точке наблюдения P сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной. Таким образом, действие всей волновой поверхности эквивалентно половине действия центральной зоны Этот же результат можно получить, если применить графический метод сложения амплитуд. Если световая волна встречает на пути своего распространения какое-либо препятствие (отверстие или преграду), то в этом случае мы разобьем на зоны Френеля волновой фронт, дошедший до этого препятствия. Понятно, что препятствие закроет часть зон Френеля, и вклад в результирующую амплитуду дадут только волны, испущенные открытыми зонами Френеля. Вы можете пронаблюдать, как меняется вид дифракционной картины в зависимости от числа открытых зон Френеля.

На основе своего метода Френель доказал, что свет распространяется практически прямолинейно.

Действительно, можно показать, что размеры зон Френеля (их радиусы) равны:.

В качестве примера рассмотрим случай, когда z0 = z1 = 1 м; λ = 0.5 мкм, тогда радиус первой (центральной) зоны равен r1 = 0.5 мм. Амплитуда в точке наблюдения P равна половине амплитуды волны, испущенной первой зоной (действие всей волновой поверхности свелось к действию ее небольшого участка), следовательно, свет от точки L к точке P распространяется в пределах очень узкого (диаметром всего один миллиметр!) канала, то есть практически прямолинейно! Показав, что свет распространяется прямолинейно, Френель с одной стороны доказал правильность своих рассуждений, а с другой преодолел препятствие, которое в течение веков стояло на пути утверждения волной теории — согласование прямолинейного распространения света с его волновым механизмом. Другим доказательством того, что метод зон Френеля дает верный результат, являются следующие рассуждения. Действие всей волновой поверхности эквивалентно половине действия центральной зоны. Если открыть только первую зону Френеля, то согласно расчетам Френеля результирующая амплитуда в точке наблюдения будет равна А1. То есть в этом случае амплитуда света в точке наблюдения увеличится в 2 (а интенсивность, соответственно, в четыре раза) по сравнению со случаем, когда открыты все зоны Френеля. Этот результат можно проверить опытным путем, поставив на пути световой волны преграду с отверстием, открывающим только первую зону Френеля. Интенсивность в точке наблюдения действительно возрастает в четыре раза по сравнению со случаем, когда преграда между источником излучения и точкой наблюдения отсутствует!

Более того, вспомним, что волны из соседних зон гасят друг друга, и все четные зоны дают вклад в результирующую амплитуду одного знака, а все нечетные зоны дают вклад противоположного знака. Это значит, что интенсивность света в точке наблюдения можно усилить во много раз, если прикрыть все четные или, наоборот, нечетные зоны Френеля. Оставшиеся неприкрытыми зоны будут усиливать действие друг друга. Эта идея лежит в основе простого оптического устройства, называемого зонной пластинкой Френеля. Зонную пластинку можно изготовить, начертив на листе бумаги темные кольца, а затем сфотографировав их в уменьшенном масштабе. Внутренние радиусы темных колец должны совпадать с радиусами нечетных зон Френеля, а внешние — с радиусами четных. Такая пластинка будет перекрывать четные зоны. Зонная пластинка фокусирует свет аналогично собирающей линзе, только в отличие от линзы пластинка имеет несколько фокусов. Существуют также фазовые зонные пластинки, которые увеличивают амплитуду еще в два раза по сравнению с обычной (амплитудной) зонной пластинкой. В такой пластинки четные (или нечетные) зоны не перекрываются. Вместо этого меняется на π фаза их колебаний. Это можно осуществить с помощью прозрачной пластинки, у которой толщина в местах, соответствующих четным (или нечетным) зонам, меняется на специально подобранную величину.

Источник

Как сделать зонную пластинку

8.1(а). Интерферометр Майкельсона.

Принцип действия всех Интерферометров одинаков, и различаются они лишь методами получения когерентных волн и тем, какая величина непосредственно измеряется. Пучок света с помощью того или иного устройства пространственно разделяется на два или большее число когерентных пучков, которые проходят различные оптические пути, а затем сводятся вместе. В месте схождения пучков наблюдается интерференционная картина, вид которой, т. е. форма и взаимное расположение интерференционных максимумов и минимумов, зависит от способа разделения пучка света на когерентные пучки, от числа интерферирующих пучков, разности их оптических путей (оптической разности хода), относительной интенсивности, размеров источника, спектрального состава света.

Примером двулучевого Интерферометр может служить Интерферометр Майкельсона (рис 1)..

Рис.1 Схема интерферометра Майкельсона (P 2 пластинка, компенсирующая дополнительную разность хода, появляющуюся за счёт того, что луч 1 проходит дважды через пластинку P 1 ).

8.1(б).Что такое зонная пластинка? Опишите принцип ее действия.

8.1(в).Что такое поляризованный свет? Какие бывают основные виды поляризации и что они означают?

Поляризованным называется свет, в котором направления колебаний светового вектора упорядочены каким-либо образом.

8.1(г). Эффект Фарадея.

Эффект Фарадея заключается в том, что в магнитном поле первоначально неактивное вещество становится оптически активным. При распространении света в веществе вдоль вектора напряженности магнитного поля плоскость поляризации световой волны вращается. Схема для наблюдения эффекта Фарадея изображена на рисунке.

Образец длиной 1 помещается в соленоид. Напряженность магнитного поля на оси соленоида Н. При включении магнитного поля плоскость поляризации света на выходе из образца поворачивается на угол относительно первоначального положения. Угол поворота плоскости поляризации равен

, где V – постоянная Верде.

Схема установки: Для наблюдения эффекта Фарадея в полюсных наконечниках электромагнита просверливают отверстия, через которые пропускают луч света. Исследуемое вещество надо поместить между полюсами магнита

Источник