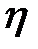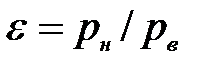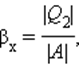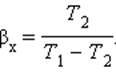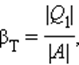Площадь термодинамического цикла тепловой машины в t s диаграмме соответствует
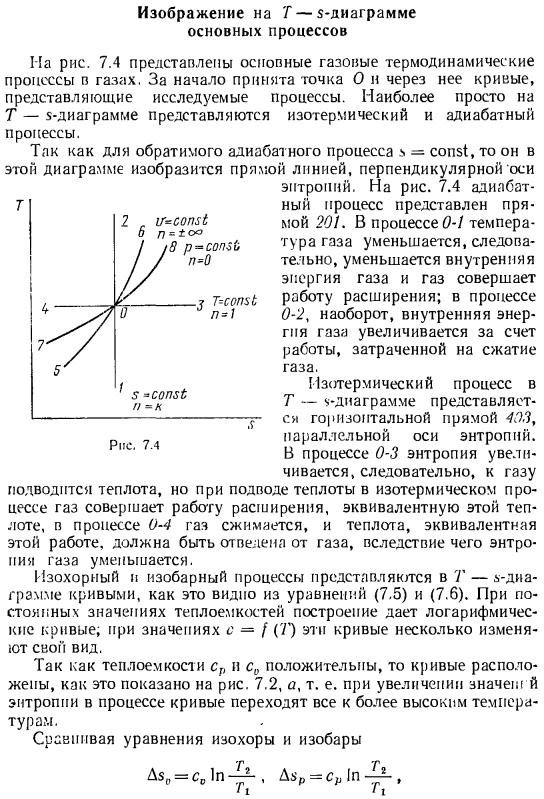
Изображение на Т-s-диаграмме основных процессов
Изображение на Т-s-диаграмме основных процессов
Рисунок 7.4 процесс термоизоляции непосредственно представлен 201.In процесс 0-1, температура газа уменьшается, поэтому внутренняя энергия газа уменьшается, и газ выполняет расширение work. In в процессе 0-2, наоборот, внутренняя энергия газа увеличивается за счет работы, затраченной на сжатие Изотермический процесс — «- Представляет собой горизонтальную линию 403, параллельную оси энтропии. В процессе от 0 до 3 энтропия увеличивается, поэтому газ подается с теплом, но в изотермическом процессе газ выполняет работу расширения, эквивалентную этой теплоте, и в процессе от 0 до 4 газ сжимается, что приводит к уменьшению энтропии газа.
Вычислите площадь поверхности, которую следует окрасить вновь после окончания сварки. Людмила Фирмаль
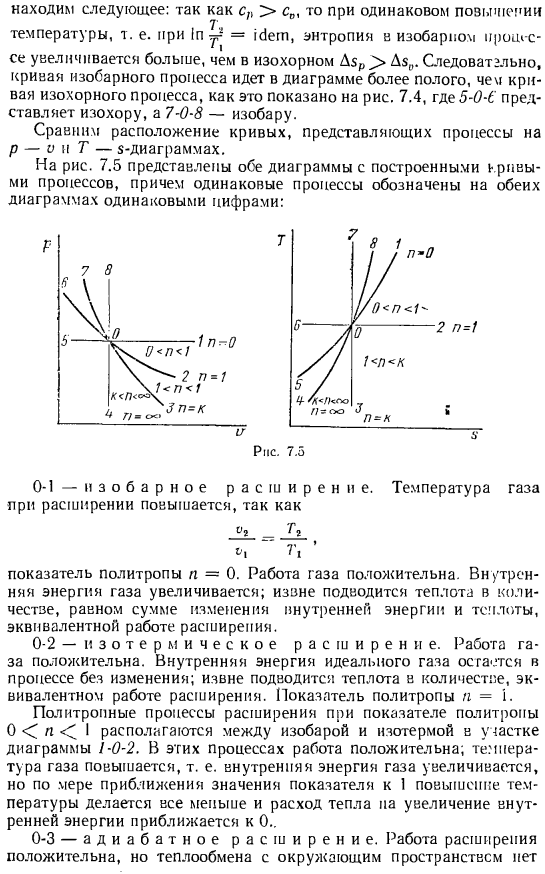
В результате кривая изобарного процесса становится более полой на диаграмме, чем кривая изобарного процесса, как показано на рисунке. 7.4, 5-0-E представляет собой изолинии, и 7-0-8 представляет собой isobarine. сравним расположение кривых, представляющих процессы на p-V и T-диаграммах. На рис. 7.5 показаны кривые процесса, построенные на обеих диаграммах, и один и тот же процесс показан на обеих диаграммах с одинаковым номером. 0-1-изобарное расширение.
То есть внутренняя энергия газа увеличивается, но при приближении значения показателя к 1、 Температура становится все меньше и увеличение теплопотребления па внутренней энергии приближается к 0. 0-3-развертывание изоляции. Работа по расширению-это плюс, но теплообмен с окружающим пространством-это питомец Таким образом, работа осуществляется за счет равного уменьшения внутренней энергии. Температура газа снижается. Показатель политропы N = й. Процесс расширения политропа, где индекс политропа равен 1 n k, лежит между изотермами и теплоизоляцией области на рисунке 2-0-3.In эти процессы, работа газа положительны. Температура газа уменьшается и внутренняя энергия.
Нужно сварить два куска стали длиной 1,83 м, шириной 0,61 м и толщиной 3,2 мм. Людмила Фирмаль
В то же время тепло поступает в газ из окружающей среды. Это можно увидеть на диаграмме p-o, где эти процессы находятся над слоем изоляции, и на диаграмме T-z, где эти процессы прогрессируют с увеличением энтропии. Следовательно, в этих процессах работа газа осуществляется за счет уменьшения подводимого извне тепла и внутренней энергии газа. Теплоемкость этих процессов отрицательна. 0-4-изометрическое охлаждение. Газ не работает, и часть его внутренней энергии выделяется в окружающую среду в виде тепла. Политропный индекс n =°O.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Площадь термодинамического цикла тепловой машины в t s диаграмме соответствует
Основные понятия и определения
В термодинамике широко используется понятие термодинамической системы.
Определение: термодинамической системой называется совокупность материальных тел, взаимодействующих, как между собой, так и с окружающей средой. Все тела находящиеся за пределами границ рассматриваемой системы называются окружающей средой.
Перечислим основные параметры состояния вещества:
В настоящее время в мире существует несколько температурных шкал и единиц измерения температуры.. Наиболее распространенная в Европе шкала Цельсия где нулевая температура – температура замерзания воды при атмосферном давлении, а температура кипения воды при атмосферном давлении принята за 100 градусов Цельсия ( ° С). В Северной Америке используется шкала Фаренгейта. Для термодинамических расчетов очень удобна абсолютная шкала или шкала Кельвина. За ноль в этой шкале принята температура абсолютного нуля, при этой температуре прекращается всякое тепловое движение в веществе. Численно один градус шкалы Кельвина равен одному градусу шкалы Цельсия.
Соотношение для перехода от градусов Цельсия к градусам Кельвина:
T-температура в Кельвинах;
t – температура в градусах Цельсия.
Для измерения давления применяются различные единицы измерения. В стандартной системе измерения СИ единицей служит Паскаль (Па).
Соотношение между единицами:
1 кг/см 2 (атмосфера) = 9.8067 ґ 10 4 Па
1мм рт. ст (миллиметр ртутного столба) = 133 Па
1 мм вод. ст. (миллиметр водного столба) 9.8067 Па
Плотность – отношение массы вещества к объему занимаемому эти веществом.
Основные термодинамические параметры состояния Р, V, Т однородного тела зависят один от другого и взаимно связаны уравнением состояния:
Для идеального газа уравнение состояния записывается в виде:
R – газовая постоянная (у каждого газа свое значение)
Если известно уравнение состояния, то для определения состояния простейших систем достаточно знать две независимые переменные из 3-х
Р = f1 (v, т); v = f2 (Р, Т); Т = f3 (v, Р)
Термодинамические процессы часто изображаются на графиках состояния, где по осям отложены параметры состояния. Точки, на плоскости такого графика, соответствуют определенному состоянию системы, линии на графике соответствуют термодинамическим процессам, переводящим систему из одного состояния в другое.
Рассмотрим термодинамическую систему, состоящую из одного тела – какого либо газа в сосуде с поршнем, причем сосуд и поршень в данном случае является внешней средой. Пусть, для примера, происходит нагрев газа в сосуде, возможны два случая:
1) Если поршень зафиксирован и объем не меняется, то произойдет повышение давления в сосуде. Такой процесс называется изохорным (v=const), идущий при постоянном объеме;
Изохорные процессы в P – T координатах:
2) Если поршень свободен, то нагреваемый газ будет расширяться, при постоянном давлении такой процесс называется изобарическим (P=const), идущим при постоянном давлении.
Изобарные процессы в v – T координатах
Изотермические процессы в P-v координатах
Примерный график адиабатного процесса в P – v координатах.
Понятие кругового процесса является для нас ключевым в термодинамике, поскольку работа АЭС основана на паро-водяном цикле, другими словами мы можем рассматривать испарение воды а активной зоне (АЗ), вращение паром ротора турбины, конденсацию пара и поступление воды в АЗ как некий замкнутый термодинамический процесс или цикл.
Первый способ передачи энергии при непосредственном контакте тел, имеющих различную температуру, путем обмена кинетической энергии между молекулами соприкасающихся тел (или лучистым переносом при помощи электромагнитных волн).
Энергия передается от более нагретого тела к менее нагретому.
Второй способ передачи энергии связан с наличием силовых полей или внешнего давления. Для передачи энергии этим способом тело должно либо передвигаться в силовом поле, либо изменять свой объем под действием внешнего давления.
Этот способ называется передачей энергии в форме работы.
Рабочим телом в реакторной установке РБМК является вода, которая после испарения в активной зоне в виде пара совершает работу в турбине, вращая ротор.
Первый закон термодинамики.
Этот закон является частным случаем всеобщего закона сохранения и превращения энергии, который гласит, что энергия не появляется и не исчезает, а только переходит из одного вида в другой.
Из этого закона следует, что уменьшение общей энергии в одной системе, состоящей из одного или множества тел, должно сопровождаться увеличением энергии в другой системе тел.
Существуют другие формулировки этого закона:
1. Не возможно возникновение или уничтожение энергии (эта формулировка говорит о невозможности возникновения энергии ни из чего и уничтожения ее в ничто);
2. Любая форма движения способна и должна превращаться в любую другую форму движения (эта философская формулировка подчеркивает неуничтожимость энергии и ее способность взаимопревращаться в любые другие виды энергии);
3. Вечный двигатель первого рода невозможен. (Под вечным двигателем первого рода понимают машину, которая была бы способна производить работу не используя никакого источника энергии);
4. Теплота и работа являются двумя единственно возможными формами передачи энергии от одних тел к другим.
Удельная энтальпия i это отношение энтальпии тела к его массе.
Удельная энтальпия это параметр состояния.
Значение удельной энтальпии пара и воды при определенном давлении и температуре можно найти в справочнике. Пользуясь этими данными, можно определить количество теплоты участвующее в процессе или работу процесса.
Теплота q не является функцией состояния, количество теплоты выделившейся или поглотившейся в процессе зависит от самого процесса. Функцией состояния является энтропия обозначается S размерность Дж/К
Удельная энтропия отношение энтропии тела к его массе. Удельная энтропия s является справочной величиной.
s = f (Р, v, Т) [Дж/кг Ч к]
Тепловая Т- S диаграмма.
Удельную энтропию можно применять совместно с одним из основных параметров для графического изображения процессов. Аналогично тому, как мы строили изменение объема в зависимости от изменения температуры, мы можем изобразить некоторый процесс изменения энтропии и температуры в Т-S координатах. В этом случае любая точка на графической плоскости соответствует определенному состоянию рабочего тела, а линия от точки 1 до точки 2 отображает некий термодинамический процесс. Особенностью Т-S координат является то, что площадь под линией процесса соответствует количеству энергии отданной или полученной рабочим телом.
Т – S диаграмма цикла Карно
На данной диаграмме представлен некий замкнутый цикл. Система последовательно переходит из точки 1 в 2 затем 3, 4 и снова в 1. Из графика видно что процесс 1 ® 2 является изотермическим (происходит при Т 1 ) и процесс 3 ® 4 также является изотермическим (происходит при T 2 )
Процессы 2 ® 3 и 4 ® 1 являются адиабатными. Поскольку в них не происходит изменение энтропии то dS = 0 следовательно dQ = 0 или Q = const.
Количество тепла подводимое к системе:
Количество тепла отдаваемое системой:
Второй закон термодинамики.
Первый закон термодинамики утверждает, что теплота может превращаться в работу, а работа в теплоту, не устанавливая условий, при которых возможны эти превращения. Повседневные наблюдения и опыты показывают, что теплота сама может переходить только от нагретых тел к более холодным (до полного равновесия). Только за счет затраты работы можно изменить направление движения теплоты. Это свойство теплоты резко отличается от работы. Работа легко и полностью превращается в теплоту.
Формулировки второго закона термодинамики:
1. Вечный двигатель второго рода не возможен (под вечным двигателем второго рода понимается машина, которая могла бы превращать всю подводимую к ней теплоту в работу. Такая машина имела бы КПД = 1).
Условия работы тепловых машин.
Тепловая машина всегда работает в определенном перепаде температур. (Это значит, что для работы такой машины необходим иметь по крайней мере 1 источник теплоты, и 1 приемник теплоты).
Любая тепловая машина должна работать циклично, т.е. рабочее тело, совершая за определенный промежуток времени ряд процессов расширения и сжатия, должно возвращаться в исходное состояние.
Циклы паросиловых установок
Как было сказано выше, реакторную установку можно представить в виде тепловой машины, в которой осуществляется некий термодинамический цикл.
Теоретическим циклом современной паросиловой установки является цикл Ренкина.
Конденсатор играет двоякую роль в установке.
Во-первых, он имеет паровое и водяное пространство, разделенные поверхностью, через которую происходит теплообмен между отработавшим паром и охлаждающей водой. Поэтому конденсат пара может быть использован в качестве идеальной воды, не содержащей растворенных солей.
Во-вторых, в конденсаторе вследствие резкого уменьшения удельного объема пара при его превращении в капельножидкое состояние наступает вакуум, который будучи поддерживаемым в течение всего времени работы установки, позволяет пару расширяться в турбине еще на одну атмосферу (Рк » 0,04-0,06 бар) и совершать за счет этого дополнительную работу.
Цикл Ренкина в T-S диаграмме.
Синяя линия в Т-S диаграмме воды является разделительной, при энтропии и температуре, соответствующим точкам, лежащим на диаграмме выше этой линии, существует только пар, ниже пароводяная смесь.
Длина отрезка 3-5 в T-S-диаграмме весьма мала, так как в области жидкости, изобары (линии постоянного давления) в T-S-диаграмме проходят очень близко друг от друга. Благодаря этому при изоэптропном (при постоянной энтропии) сжатии воды, температура воды возрастает менее чем на 2-3 ° С, и можно с хорошей степенью приближения считать, что в области жидкости изобары воды практически совпадают с левой пограничной криво (синяя линия); поэтому зачастую при изображении цикла Ренкина в Т-S-диаграмме изобары в области жидкости изображают сливающимися с левой пограничной кривой. Малая величина отрезка адиабаты 3-5 свидетельствует о малой работе, затрачиваемой насосом на сжатие воды. Малая величина работы сжатия по сравнению с величиной работы, производимой водяным паром в процессе расширения 1-2, является важным преимуществом цикла Ренкина.
С точки зрения термического к. п. д. цикл Ренкина представляете менее выгодным, чем цикл Карно, изображенный выше, поскольку степень заполнения цикла (равно как и средняя температур подвода тепла) для цикла Ренкина оказывается меньше, чем в случае цикла Карно. Однако с учетом реальных условий осуществления экономичность цикла Ренкина выше экономичности соответствующего цикла Карно во влажном паре.
Поскольку в настоящее время не существует промышленных энергетических установок с ядерным перегревом пара (перегрев пара непосредственно в активной зоне ядерного реактора), то для одноконтурных ядерных реакторов BWR и РБМК используется цикл с промежуточным перегревом пара.
Т-S диаграмма цикла с промежуточным перегревом пара.
Для повышения КПД в цикле с промежуточным перегревом пара, используется двух ступенчатая турбина, состоящая из цилиндра высокого давления и нескольких (4 для РБМК) цилиндров низкого давления. Пар из барабана сепаратора направляется в цилиндр высокого давления (ЦВД), часть пара отбирается для перегрева. Расширяясь в цилиндре высокого давления процесс на диаграмме 1-6, пар совершает работу. После ЦВД пар направляется в пароперегреватель, где за счет охлаждения отобранной в начале части пара, осушается и нагревается до более высокой температуры, (но уже при более низком давлении, процесс 6-7 на диаграмме) и поступает в цилиндры низкого давления турбины (ЦНД). В ЦНД пар расширяясь, снова совершает работу (процесс 7-2 на диаграмме) и поступает в конденсатор. Остальные процессы соответствуют процессам в выше рассмотренном цикле Ренкина.
Малое значение КПД цикла Ренкина по сравнению с циклом Карно связано с тем, что большое количество тепловой энергии при конденсации пара передается охлаждающей воде в конденсаторе. Для снижения потерь часть пара из турбины отбирается и направляется на регенерационные подогреватели, где тепловая энергия, высвобождаемая при конденсации отобранного пара, используется для подогрева воды, полученной после конденсации основного парового потока.
В реальных паросиловых циклах регенерация осуществляется с помощью регенеративных, поверхностных или смешивающих, теплообменников, в каждый из которых поступает пар из промежуточных ступеней турбины (так называемый регенеративный отбор). Пар конденсируется в регенеративных теплообменниках, нагревая питательную воду, поступающую в реактор. Конденсат греющего пара смешивается с основным потоком питательной воды.
Схема установки с регенеративным циклом.
Стрелками показаны отборы пара из турбины.
Диаграмма состояния вещества, i,s-диаграмма
Изображение циклов и процессов в T-S диаграмме обладает большой наглядностью, поскольку площади на данной диаграмме соответствуют работе или энергии процесса. Эта наглядность позволяет визуально сравнивать различные процессы и циклы, однако эта наглядность является одновременно и недостатком Т-S диаграммы, поскольку измерить площадь сложной фигуры очень сложна, а все основные циклы, как мы видели, представляют собой именно комбинацию сложных кривых, исключение составляет только цикл Карно.
В тепловых расчетах паросиловых циклов используется диаграмма состояния воды. На рисунке изображен цикл с перегревом пара на диаграмме состояния воды (см. рис.).
Вода с параметрами соответствующими точке 3 на диаграмме поступает в насос. Где происходит процесс адиабатного сжатия воды от давления Р 2 до давления Р 1 по линия процесса 3-5. Линия 5-4, это линия нагрева воды до температуры насыщения Т 3 при постоянном давлении Р 1 этот участок не является прямой линией, а представляет собой некую кривую.
Процесс 6-1 это процесс перегрева пара при постоянном давлении P 1 =сonst. В точке 6 происходит разделения линий процессов изобарического (изобара P 1 =сonst) и точки изотермического (изотерма Т 3 =const). По линии 6-1 пар нагревается до температуры Т 1 –цикл замкнулся.
Тепловые двигатели. Термодинамические циклы. Цикл Карно
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.
Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0):
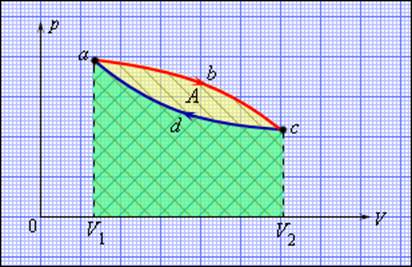
Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу A1, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A = A1 + A2 на диаграмме (p, V) равна площади цикла. Работа A положительна, если цикл обходится по часовой стрелке, и A отрицательна, если цикл обходится в противоположном направлении.
Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 0, A > 0, Q2 T2
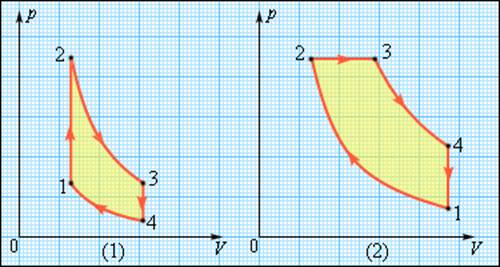
В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.
Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2)
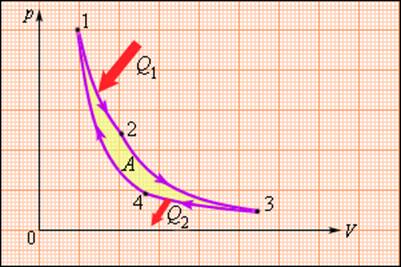
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 0, T1 > T2
Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q2| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением
т. е. эффективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении βх может быть и больше, и меньше единицы. Для обращенного цикла Карно
Если полезным эффектом является передача некоторого количества тепла |Q1| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность βТ теплового насоса может быть определена как отношение
т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
следовательно, βТ всегда больше единицы. Для обращенного цикла Карно
Сжатие реального газа сопровождается изменением его объема, давления и температуры. Соотношение между этими параметрами при давлении не более 10 6 н/м 2 (
10 am ) характеризуется уравнением состояния идеальных газов.
При давлениях более 10 6 н/м 2 ( p >10 am ) следует пользоваться уравнением Ван-дер-Ваальса или другим уравнением более точно описывающим зависимость между объемом, давлением и температурой газа при повышенных давлениях.
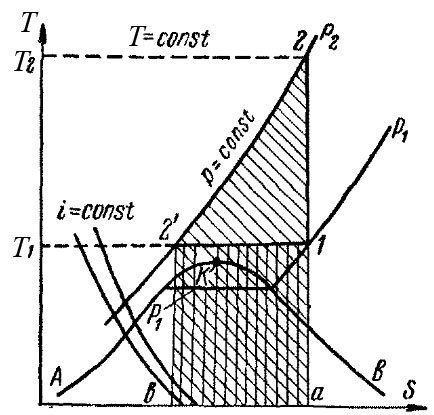
Процессы сжатия газа наглядно могут быть изображены на энтропийной, или тепловой, диаграмме Т–S (рис. 7-28).
На оси ординат этой диаграммы откладывается абсолютная температура (Т), по оси абсцисс – энтропия (S). Как известно из термодинамики, энтропия представляет собой некоторую функцию состояния тела, которая увеличивается при подводе к нему тепла, причем это увеличение тем меньше, чем выше температура тела.
Приращение энтропии при подводе тепла q дж/кг составляет при обратимом процессе
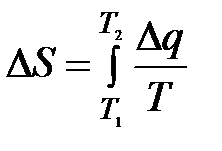 дж/кг∙град дж/кг∙град | (7-31) |
На Т – S диаграмме нанесены линии, соответствующие постоянному давлению (изобары), и линии, соответствующие постоянной температуре (изотермы), которые изображаются горизонтальными прямыми. Линия АКВ является пограничной кривой. Область, лежащая ниже этой кривой, соответствует влажному пару, ветвь АК – жидкости при температуре насыщения, ветвь КВ – сухому насыщенному пару. Точка К является критической точкой. Слева от ветви АК находится область жидкости, справа от ветви КВ – область перегретого пара. Так как испарение и конденсация жидкости протекают при постоянных температурах и давлениях, то в области влажного пара изобары совпадают с изотермами. Конденсация смеси влажных паров протекает при переменной температуре, поэтому в таких случаях изобары в области влажного пара не совпадают с изотермами.
Кроме того, на Т–S – диаграмме (рис. 7-28) нанесены линии постоянной энтальпии (i = const). Энтальпия идеальных газов зависит только от температуры, и для таких газов линии i = const совпадают с изотермами. Энтальпия реальных газов зависит также от давления и для них линии i = const не совпадают с изотермами.
Процессы сжатия газа в компрессоре изображаются на диаграмме Т–S следующим образом. При адиабатическом сжатии q = 0, следовательно по формуле (7-31) ∆S = 0, т.е. процесс идет без изменения энтропии (S = const). Поэтому процесс изображается вертикальной линией 1–2, причем точка 1 характеризует состояние газа до сжатия и лежит на пересечении изобары p1 и изотермы T1; точка 2 отвечает состоянию газа после сжатия и лежит на изобаре, соответствующей давлению p2.
Рис. 7-28 – Диаграмма T–S процесса сжатия газа
При изотермическом сжатии процесс протекает при T=const и изображается горизонтальной линией 1–2′ причем точка 2′, характеризующая состояние газа после сжатия, лежит на изобаре p2. Количество отводимого тепла q, согласно формуле (7-31), составляет T∆S и на рис. 7-28 выражается площадью заштрихованного прямоугольника а–1–2’–b, высота которого равна T1, а основание – изменению энтропии ∆S. В данном процессе энтропия уменьшается, т.е. величина ∆S отрицательна. Поэтому количество тепла будет также отрицательным, т.е. процесс сопровождается, как указывалось выше, отводом тепла. Та же площадь а–1–2’–b выражает работу изотермического сжатия в тепловых единицах, а площадь а–2–2’–b на рис. 7-28 равна работе адиабатического сжатия.
Уравнения состояния газа
В основу описаний конкретных процессов сжатия газов положено уравнение состояния идеального газа Клапейрона:
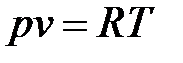

Изотермный процесс сжатия газов характеризуется постоянством температуры в процессе, для которого Т = const, и, следовательно, dT = 0.
В этом случае уравнение (9.28) имеет вид
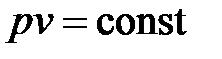
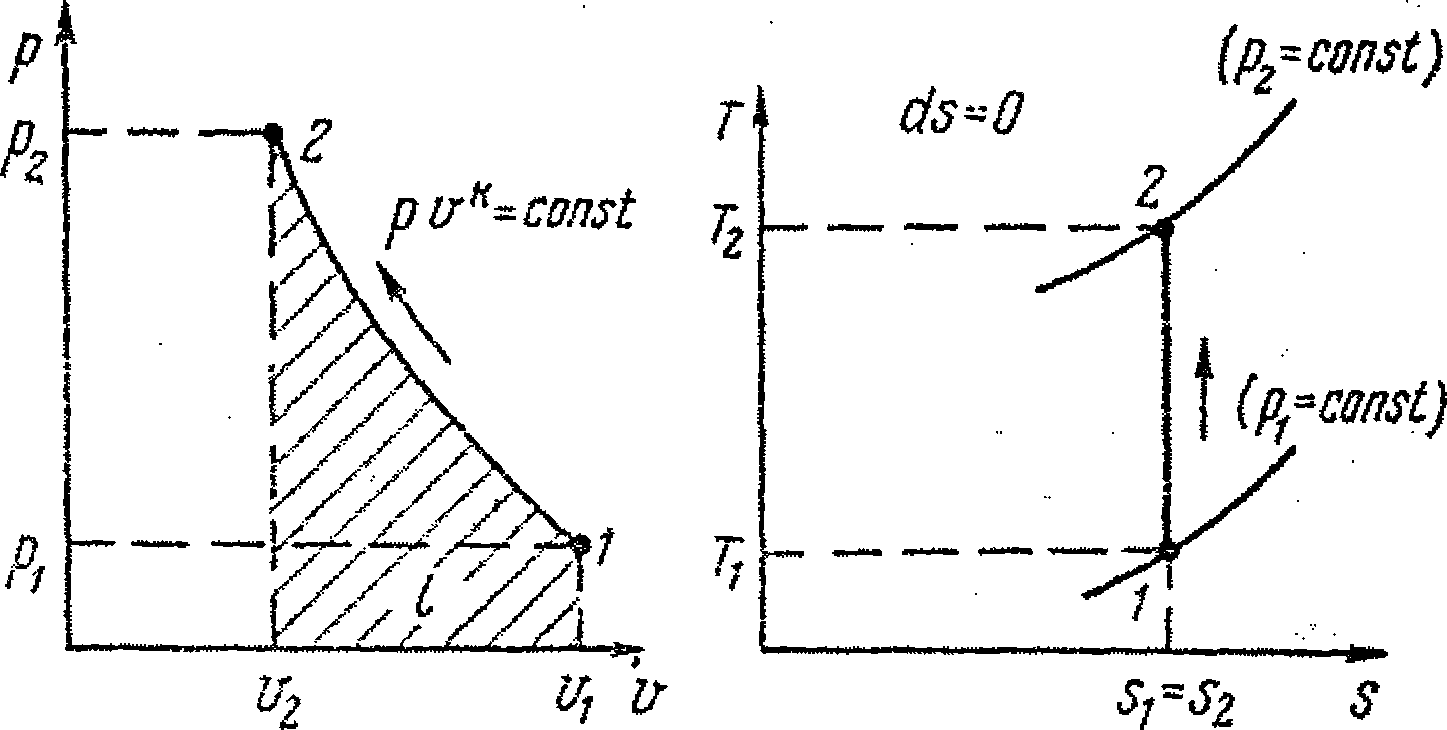
Адиабатным называется процесс сжатия газов, который протекает в теплоизолированной системе. В этом процессе отсутствует отвод тепла, выделяющегося при сжатии газов, т. е.
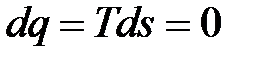

Поскольку энтропия процесса ds = dq / T, то при адиабатном процессе сжатия газов ds = 0, т. е. s = const, т. е. вся механическая энергия сжатия затрачивается на приращение внутренней энергии.
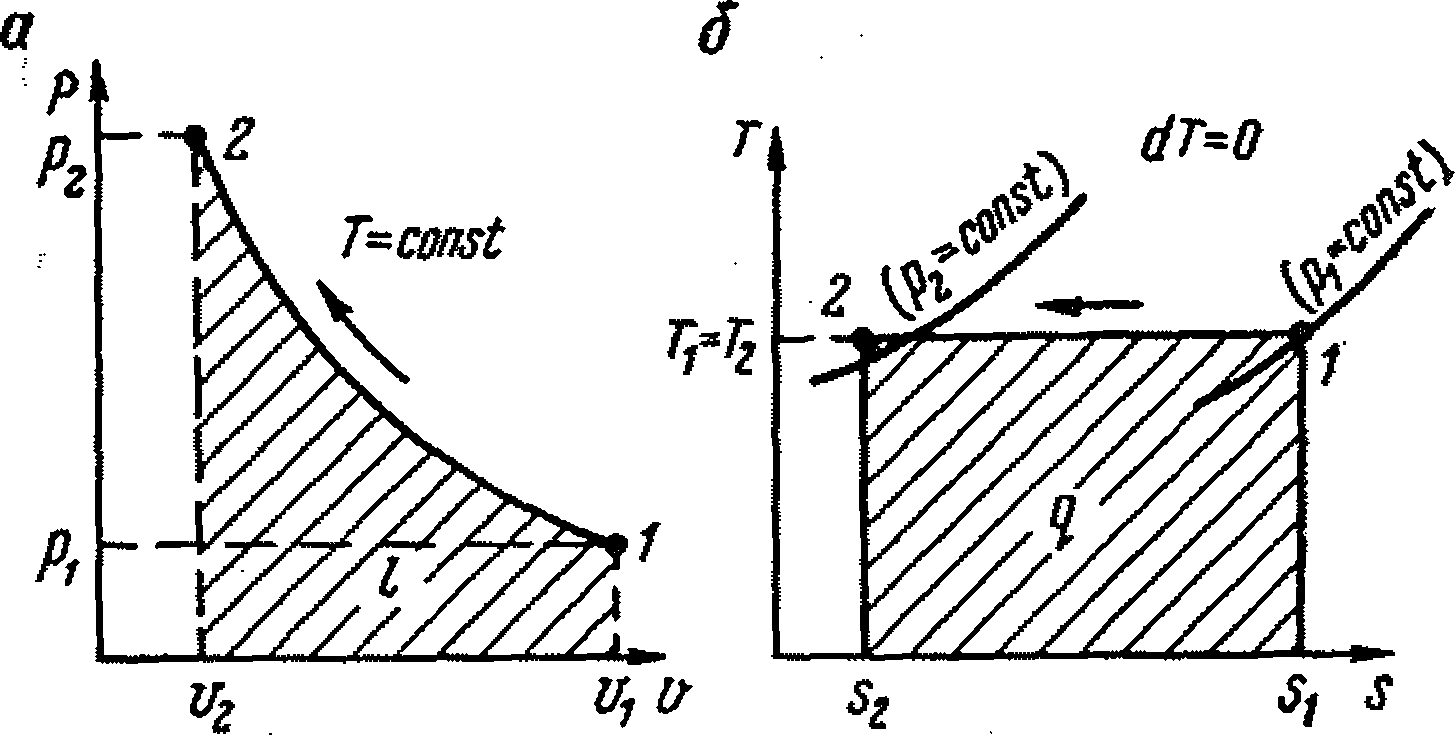
Линии 1-2 адиабатного процесса сжатия газа в координатах р-v и Т-s приведены на рис. 9.3, а, б.
Ранее было указано, что термическая работа (выделенное тепло)
а величина к = cp / cv называется показателем адиабаты.
Реальные процессы при работе компрессоров не являются адиабатными, так как в процессе сжатия имеется теплообмен, т. е. dq 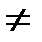
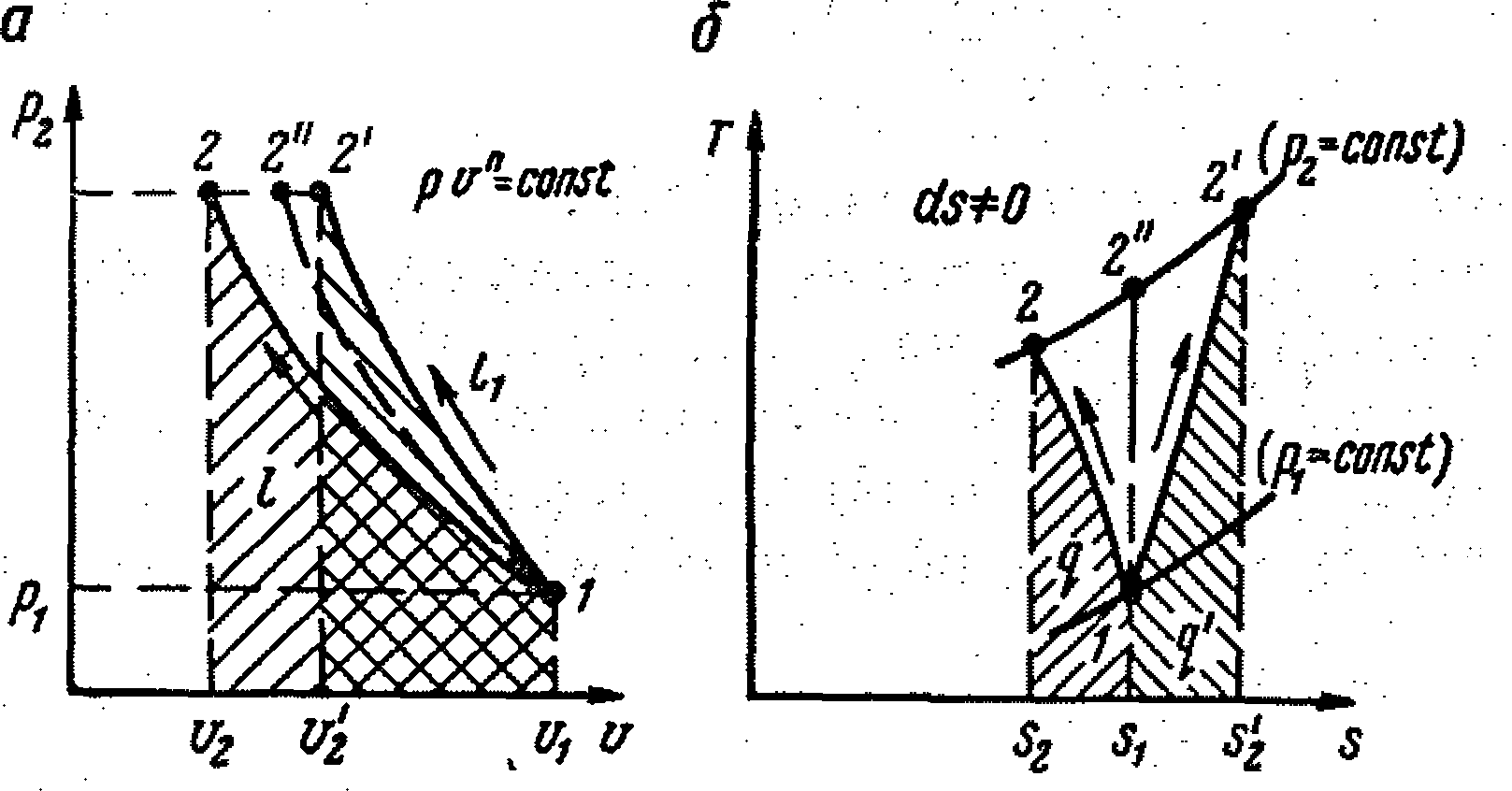
Подобные процессы сжатия газов называются политропными.
По аналогии с адиабатным процессом уравнение состояния политропного процесса
является уравнением политропы, в котором число п называется показателем политропы.
Таким образом, чтобы найти показатель политропы, надо определить р и v для каких-либо двух точек процесса.
Политропный процесс сжатия газа (рис. 9.4, а, б) может быть осуществим как с отводом тепла (процесс компримирования в обычных компрессорах).
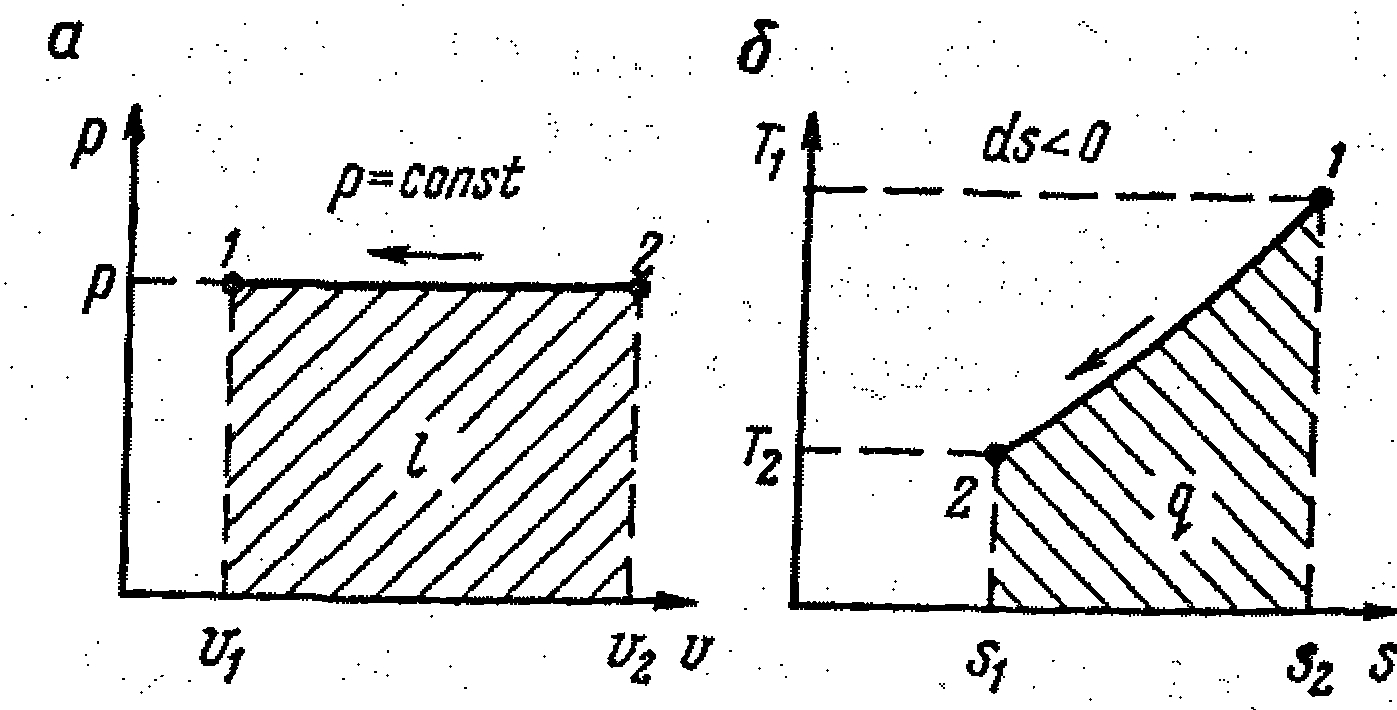
В идеальном компрессоре процесс заполнения цилиндра компрессора газом, а также вытеснение из цилиндра газа после окончания процесса сжатия должен производиться при постоянных давлениях р1 и р2.
Если рассмотреть уравнение состояния (9.28), то изобарный процесс будет соответствовать закону Гей-Люссака:
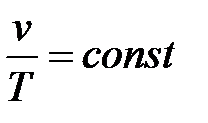
так как R / p = const.
Как видно из рис. 9.5, работа, затрачиваемая на сжатие газа,

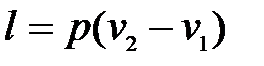
Собственно сжатия как такового, т. е. повышения давления газа, в этом случае нет. Есть просто процесс вытеснения газа, т. е. приведение объема 
к объему 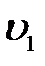
Величина уменьшения энтропии, аналогично (9.51), равна:
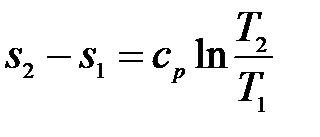
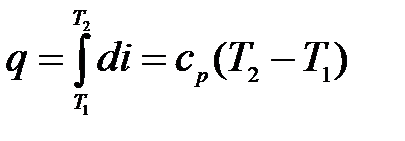
Таким образом, если за общее уравнение состояния принять уравнение политропного процесса (9.48), то уравнения рассмотренных выше процессов будут являться его частными случаями: при n = к для адиабатного процесса; при n = 1 для изотермного процесса; при п = 0 для изобарного процесса.
Компрессоры проектируются и выпускаются с определёнными показателями (характеристиками) работы, которые должны удовлетворять условиям их применения.
К ним относятся: производительность компрессора Q в м 3 /с; развиваемый напор (давление) р в Н/м 2 ; потребляемая мощность N в кВт; коэффициент полезного действия