алгоритм судного дня что такое
Алгоритм Судного дня
Алгоритм (метод) Судного дня (англ. Doomsday algorithm ) — простой алгоритм для определения дня недели данной даты. Он был разработан около 1970 года британским математиком Джоном Конвеем.
Алгоритм для устного счёта действителен для григорианского календаря, но есть модификации для юлианского. Он ориентируется на так называемый «Судный день» (англ. Doomsday ). Так в данном контексте назван последний день февраля, то есть 28 или (в високосном году) 29 февраля.
Если известен день недели «судного дня» в данном году, можно использовать последний день февраля как основу для расчёта дня недели всех остальных дат этого года. Рекомендуется запомнить день недели «судного дня» актуального года (в 2012 году это среда). В каждом году он смещается на один день, в високосных годах на два.
«Шпаргалка»
Литература
Ссылки
Полезное
Смотреть что такое «Алгоритм Судного дня» в других словарях:
Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и … Википедия
Конвей, Джон Хортон — Джон Хортон Конвей англ. John Horton Conway … Википедия
BGM-71 TOW — «Тоу» BGM 71 TOW Ракета TOW, запущенная с джипа F … Википедия
Шамир, Исраэль — Проверить нейтральность. На странице обсуждения должны быть подробности … Википедия
Искусственная жизнь — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Искусственн … Википедия
Исраэль Шамир — (Израиль Соломонович Шмерлер; p. 1947, Новосибирск; известный в Швеции как Ёран Ермас) российско израильский писатель, переводчик и публицист антисионистской направленности. Был признан антисемитом Французским судом.[1] Исраэль Шамир Изя (Израиль … Википедия
Шамир Исраэль — Исраэль Шамир (Израиль Соломонович Шмерлер; p. 1947, Новосибирск; известный в Швеции как Ёран Ермас) российско израильский писатель, переводчик и публицист антисионистской направленности. Был признан антисемитом Французским судом.[1] Исраэль… … Википедия
Хованский, Иван Андреевич Тараруй — Не следует путать с Иваном Андреевичем Большим Хованским военным деятелем начала XVII века. В Википедии есть статьи о других людях с такой фамилией, см. Хованский. князь Иван Андреевич Хованский … Википедия
Чествуем игривое волшебство Джона Хортона Конвея
Всем привет. В преддверии старта продвинутого курса «Математика для Data Science», подготовили для вас перевод статьи, которая была написана в память о легендарном математике Джоне Хортоне Конвее.
Предлагаем вам развлечь себя, решая числовую головоломку, геометрический пазл, а также играя в игру со случайными узорами, вдохновленные игривым гением легендарного математика.
Большая часть серьезных математических работ Конвея также проистекает из его слабости к математическим играм. Он внес оригинальный вклад в теорию групп (Решётка Лича, гипотеза чудовищного вздора), многомерную геометрию, тесселяцию (мозаику), теорию узлов, теорию чисел (сюрреалистические числа), алгебру, математическую логику и анализ.
В этом месяце мы чествуем игривый гений известного британского математика двумя головоломками и исследовательской игрой. Сначала мы поиграем с числовой головоломкой, изобретенной Конвеем, которая без лишней скромности является воплощением самого совершенства. Затем насладимся геометрическим пазлом, относящимся к некоторым из его наиболее визуально доставляющих работ. И наконец, мы погрузимся в игру с открытым финалом, созданную читателем Quanta, которая напоминает культовую игру “Жизнь” Конвея.
Головоломка 1: Цифровое совершенство
Существует загадочное десятичное 10-значное число abcdefghij. Все его цифры разные, и они обладают следующими свойствами:
abcde делится на 5
abcdef делится на 6
abcdefg делится на 7
abcdefgh делится на 8
abcdefghi делится на 9
abcdefghij делится на 10
Прежде чем приступить к решению этой головоломки, уделите минутку, чтобы полюбоваться абсолютным совершенством ее формы. Он излагается совершенно естественно, без малейших произвольностей или ухищрений. Прочитав первые два условия, вы точно знаете, в чем будет заключаться остальная часть головоломки. А когда этот естественный набор условий результирует в уникальном ответе, это просто восхитительно. Для меня, как создателя головоломок, эта головоломка с подстановкой цифр вызывает то же чувство, которое Моцарт внушал Эйнштейну, который сказал, что музыка Моцарта «была настолько чистой, что казалось, что она всегда присутствовала во Вселенной, ожидая, чтобы ее открыл мастер. » Только такой численно одаренный человек, как Конвей, мог уловить такую совершенную платоническую форму из райского сада головоломок!
Вы, конечно, можете решить эту головоломку, совершив поиск методом перебора с помощью компьютера, но это совсем не обязательно. Я призываю вас сделать это с помощью карандаша и бумаги. Все головоломки с подстановкой цифр такого типа могут быть решены с помощью двухэтапного процесса, знакомого тем, кто решал судоку: сначала вы устанавливаете отношения между цифрами, что сужает возможности, а затем вы проводите систематический поиск неизвестных цифр методом проб и ошибок. Здесь вам следует использовать уловки, которым вы научились в школе, чтобы определить, делится ли число на данную цифру. Если вы выжмите максимум из условий головоломки, у вас не останется слишком много кандидатов для поиска методом проб и ошибок.
Если же вы хотите усложнить себе задачу, попробуйте решить эту головоломку полностью в своей голове. В конце концов, Конвей был известен тем, что решал математические задачи «голыми руками». Это требует большого внимания и терпения, но я уверяю вас, что это возможно.
Головоломка 2: Двойственные треугольники
Есть равнобедренный треугольник, который содержит угол равный x градусов. Отношение двух сторон разной длины равно y.
Оказывается, не один, а целых два разных треугольника имеют одинаковые значения x и y!
Каковы значения x и y для этих двух равнобедренных треугольников? Что особенного в этих треугольниках и какое отношение они имеют к творчеству Конвея?
Головоломка 3: Случайные волосатые узоры
У вас есть бесконечная плоскость, на которой вы размещаете квадратные тайлы. Вы должны поочередно добавлять новые тайлы случайным образом, так чтобы каждый новый тайл имел по крайней мере одно общее ребро с ранее размещенным тайлом. Вероятность размещения тайла в любом конкретном месте пропорциональна количеству ребер ранее размещенных тайлов, которые граничат с этим местом.
Рассмотрим два примера:
Если у вас пока есть только один тайл, то второй тайл имеет равную вероятность оказаться на севере, юге, востоке или западе от исходного тайла.
Если у вас есть кольцо из восьми тайлов, то есть 12 позиций вокруг внешних сторон кольца и одна позиция в середине, и все они действительны для размещения следующего тайла. Для той, что посередине, вероятность получит тайл в четыре раза больше, чем для любой внешней подходящей позиции, потому что у нее четыре общих края с ранее размещенными тайлами, а не только одна.
Мы оцениваем “волосатость” (H, потому что в оригинале используется “hairiness”) или “внешность” любой конфигурации как количество открытых ребер тайлов, деленное на количество тайлов. Например:
Для одного тайла на плоскости H = 4 ребра ÷ 1 тайл = 4.
Для кольца из восьми тайлов H = 16 ребер ÷ 8 тайлов = 2.
Для ряда из восьми тайлов H = 18 ребер ÷ 8 тайлов = 2,25.
Величину, обратную H, можно назвать “внутренностью” или компактностью конфигурации.
(В этом видео 2014 года Numberphile(числофил) Джон Конвей рассказывает, как он создавал игру “Жизнь”.)
Вот несколько вопросов, которые направят ваше исследование этого квадратного мира.
Новый тайл может быть помещен рядом с одним ребром (касаясь только одного другого тайла), в углу (касаясь двух), внутри буквы «U» (касаясь трех) или внутри отверстия (касаясь всех четырех). Как каждое размещение влияет на количество открытых ребер в новой конфигурации (узоре)?
Каковы минимальные и максимальные значения H и каким типам тайловых узоров они соответствуют? Можете ли вы придумать приблизительную или точную формулу для максимального и минимального значений H по мере увеличения количества тайлов (n)?
Какое ожидаемое значение H (приблизительное или точное) для данного значения n?
Найдите наименьший узор, которая является «сбалансированным», так что добавление следующего тайла с такой же вероятностью увеличивает количество открытых ребер, как и уменьшает его. Сможете ли вы найти симметричный узор, обладающую этим свойством?
Найдите наименьший узор, для которой ожидаемое значение H остается неизменным после добавления еще одного тайла. Для какого следующего наименьшего по количеству тайлов узора справедливо это свойство?
Вот и все для начала. Теперь вы можете исследовать эту игру самостоятельно. Попробуйте найти ответы на несколько новых интересных вопросов. Может быть, вы найдете новую структуру (пожалуйста, поделитесь изображения интересных узоров!) Или даже докажете теорему. И пока вы это делаете, предложите название этой игре.
Алгоритм достаточно прост, чтобы его можно было вычислить мысленно. Обычно Конвей мог дать правильный ответ менее чем за две секунды. Чтобы улучшить свою скорость, он практиковал свои календарные вычисления на своем компьютере, который был запрограммирован так, чтобы опрашивать его со случайными датами каждый раз, когда он входил в систему.
СОДЕРЖАНИЕ
Якорные дни для некоторых современных лет
Якорным днем Судного дня для текущего года по григорианскому календарю (2021 г.) является воскресенье. Для некоторых других современных лет:
| Пн. | Вт. | Мы б. | Чт. | Пт. | Суббота. | Солнце. |
|---|---|---|---|---|---|---|
| 1898 г. | 1899 г. | 1900 г. | 1901 г. | 1902 г. | 1903 г. | → |
| 1904 г. | 1905 г. | 1906 г. | 1907 г. | → | 1908 г. | 1909 г. |
| 1910 г. | 1911 г. | → | 1912 г. | 1913 г. | 1914 г. | 1915 г. |
| → | 1916 г. | 1917 г. | 1918 г. | 1919 г. | → | 1920 г. |
| 1921 г. | 1922 г. | 1923 г. | → | 1924 г. | 1925 г. | 1926 г. |
| 1927 г. | → | 1928 г. | 1929 г. | 1930 г. | 1931 г. | → |
| 1932 г. | 1933 г. | 1934 г. | 1935 г. | → | 1936 г. | 1937 г. |
| 1938 г. | 1939 г. | → | 1940 г. | 1941 г. | 1942 г. | 1943 г. |
| → | 1944 г. | 1945 г. | 1946 г. | 1947 г. | → | 1948 г. |
| 1949 г. | 1950 | 1951 г. | → | 1952 г. | 1953 г. | 1954 г. |
| 1955 г. | → | 1956 г. | 1957 г. | 1958 г. | 1959 г. | → |
| 1960 г. | 1961 г. | 1962 г. | 1963 г. | → | 1964 г. | 1965 г. |
| 1966 г. | 1967 | → | 1968 г. | 1969 г. | 1970 г. | 1971 г. |
| → | 1972 г. | 1973 | 1974 г. | 1975 г. | → | 1976 г. |
| 1977 г. | 1978 г. | 1979 г. | → | 1980 г. | 1981 г. | 1982 г. |
| 1983 г. | → | 1984 г. | 1985 г. | 1986 г. | 1987 г. | → |
| 1988 г. | 1989 г. | 1990 г. | 1991 г. | → | 1992 г. | 1993 г. |
| 1994 г. | 1995 г. | → | 1996 г. | 1997 г. | 1998 г. | 1999 г. |
| → | 2000 г. | 2001 г. | 2002 г. | 2003 г. | → | 2004 г. |
| 2005 г. | 2006 г. | 2007 г. | → | 2008 г. | 2009 г. | 2010 г. |
| 2011 г. | → | 2012 г. | 2013 | 2014 г. | 2015 г. | → |
| 2016 г. | 2017 г. | 2018 г. | 2019 г. | → | 2020 г. | 2021 г. |
| 2022 г. | 2023 г. | → | 2024 г. | 2025 г. | 2026 г. | 2027 г. |
| → | 2028 г. | 2029 г. | 2030 г. | 2031 г. | → | 2032 г. |
| 2033 г. | 2034 г. | 2035 г. | → | 2036 г. | 2037 г. | 2038 |
| 2039 г. | → | 2040 г. | 2041 г. | 2042 г. | 2043 г. | → |
| 2044 | 2045 г. | 2046 | 2047 | → | 2048 | 2049 г. |
| 2050 г. | 2051 | → | 2052 | 2053 | 2054 г. | 2055 |
| → | 2056 | 2057 | 2058 | 2059 | → | 2060 |
| 2061 | 2062 | 2063 | → | 2064 | 2065 | 2066 г. |
| 2067 | → | 2068 | 2069 | 2070 | 2071 | → |
| 2072 | 2073 | 2074 | 2075 | → | 2076 | 2077 |
| 2078 | 2079 | → | 2080 г. | 2081 | 2082 | 2083 |
| → | 2084 | 2085 | 2086 | 2087 | → | 2088 |
| 2089 | 2090 | 2091 | → | 2092 | 2093 | 2094 |
| 2095 | → | 2096 | 2097 | 2098 | 2099 | 2100 |
Памятные даты, которые всегда приходятся на Судный день
Можно найти день недели данной календарной даты, используя ближайший конец света в качестве ориентира. Чтобы помочь с этим, ниже приводится список легко запоминающихся дат каждого месяца, который всегда приходится на конец света.
Судный день также приходится на несколько общих праздников. В приведенной ниже таблице включены только даты, указанные в мнемониках перечисленных источников.
Поскольку судный день определенного года напрямую связан с днями недели в период с марта по февраль следующего года, обычные и високосные годы следует различать для января и февраля того же года.
Январь и февраль можно рассматривать как последние два месяца предыдущего года.
Пример
Мнемонические названия дней недели
Поскольку этот алгоритм включает обработку дней недели как чисел по модулю 7, Джон Конвей предложил рассматривать дни недели как «Noneday»; или как «Сандай» (для воскресенья), «Один день», «Два дня», «Тройной день», «Четвертый день», «Пятидневный день» и «Шесть в день», чтобы вспомнить соотношение числа и дня недели без необходимости сосчитайте их в голове.
| день недели | Порядковый номер | Мнемонический |
|---|---|---|
| Воскресенье | 0 | Noneday или Sansday |
| понедельник | 1 | Один день |
| вторник | 2 | Два дня |
| среда | 3 | Treblesday |
| четверг | 4 | Четвертый день |
| Пятница | 5 | Пятидневка |
| Суббота | 6 | Шесть в день |
В поисках якорного дня года
Сначала возьмем день якоря для века. Согласно правилу судного дня, век начинается с 00 и заканчивается 99 годом. В следующей таблице показаны дни якоря веков 1800–1899, 1900–1999, 2000–2099 и 2100–2199.
Для григорианского календаря:
Математическая формула 5 × ( c mod 4) mod 7 + вторник = якорь. Алгоритмический Пусть r = c mod 4 если r = 0, то якорь = вторник если r = 1, то якорь = воскресенье если r = 2, то якорь = пятница если r = 3, то якорь = среда
Для юлианского календаря:
6 c mod 7 + воскресенье = якорь.
Затем найдите день привязки года. Для этого, по словам Конвея:
Например, для 1966 года двадцатого века:
Как описано в пункте 4 выше, это эквивалентно:
Итак, конец света 1966 года пришелся на понедельник.
Точно так же конец света в 2005 году приходится на понедельник:
Почему это работает
Расчет дня привязки Судного дня фактически вычисляет количество дней между любой заданной датой в базовом году и той же датой в текущем году, а затем берет остаток по модулю 7. Когда обе даты наступают после високосного дня (если есть), разница лишь 365 г + у / 4 (округлено в меньшую сторону). Но 365 равно 52 × 7 + 1, поэтому после вычисления остатка мы получаем просто
Это дает более простую формулу, если удобно делить большие значения y на 4 и 7. Например, мы можем вычислить
что дает тот же ответ, что и в приведенном выше примере.
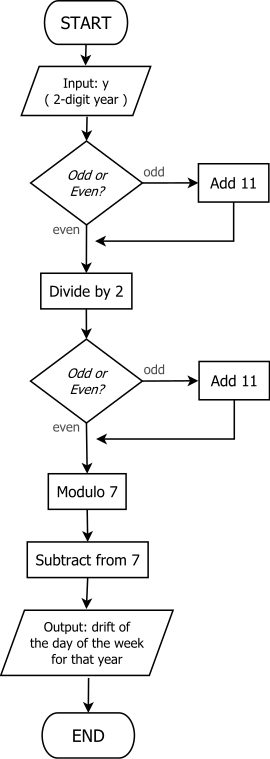
Метод «нечетное + 11»
Более простой метод определения дня привязки года был открыт в 2010 году Чемберленом Фонгом и Майклом К. Уолтерсом и описан в их статье, представленной на 7-м Международном конгрессе по промышленной и прикладной математике (2011). Метод, называемый «нечетным + 11», эквивалентен вычислению
Он хорошо подходит для мысленных вычислений, поскольку не требует деления на 4 (или 12), и процедуру легко запомнить, поскольку в ней многократно используется правило «нечетное + 11».
Расширяя это, чтобы получить день привязки, процедура часто описывается как накопление промежуточной суммы T за шесть шагов, как показано ниже:
Например, применив этот метод к 2005 году, шаги, как описано, будут следующими:
Явная формула для метода нечетных + 11:
Хотя это выражение выглядит пугающим и сложным, на самом деле оно простое из-за общего подвыражения у + 11 ( у мод 2) / 2 это нужно рассчитать только один раз.
Переписка с доминантским письмом
Судный день связан с доминирующей буквой года следующим образом.
| Конец света | Доминическое письмо | |
|---|---|---|
| Общий год | Високосный год | |
| Воскресенье | C | ОКРУГ КОЛУМБИЯ |
| понедельник | B | CB |
| вторник | А | BA |
| среда | г | AG |
| четверг | F | GF |
| Пятница | E | FE |
| Суббота | D | ED |
Найдите в приведенной ниже таблице доминирующую букву (DL).
| Сотни лет | D L | Цифры оставшегося года | # | ||||
|---|---|---|---|---|---|---|---|
| Юлиан (r ÷ 7) | Григорианский (r ÷ 4) | ||||||
| r5 19 | 16 20 r0 | А | 00 06 17 23 | 28 34 45 51 | 56 62 73 79 | 84 90 | 0 |
| r4 18 | 15 19 r3 | г | 01 07 12 18 | 29 35 40 46 | 57 63 68 74 | 85 91 96 | 1 |
| r3 17 | N / A | F | 02 13 19 24 | 30 41 47 52 | 58 69 75 80 | 86 97 | 2 |
| r2 16 | 18 22 r2 | E | 03 08 14 25 | 31 36 42 53 | 59 64 70 81 | 87 92 98 | 3 |
| r1 15 | N / A | D | 09 15 20 26 | 37 43 48 54 | 65 71 76 82 | 93 99 | 4 |
| r0 14 | 17 21 r1 | C | 04 10 21 27 | 32 38 49 55 | 60 66 77 83 | 88 94 | 5 |
| r6 13 | N / A | B | 05 11 16 22 | 33 39 44 50 | 61 67 72 78 | 89 95 | 6 |
Обзор всех Судных дней
| Месяц | Даты | Номера недель * |
|---|---|---|
| Январь (обычные годы) | 3, 10, 17, 24, 31 | 1–5 |
| Январь (високосные годы) | 4, 11, 18, 25 | 1–4 |
| Февраль (обычные годы) | 7, 14, 21, 28 | 6–9 |
| Февраль (високосные годы) | 1, 8, 15, 22, 29 | 5–9 |
| Март | 7, 14, 21, 28 | 10–13 |
| апреля | 4, 11, 18, 25 | 14–17 |
| Май | 2, 9, 16, 23, 30 | 18–22 |
| июнь | 6, 13, 20, 27 | 23–26 |
| июль | 4, 11, 18, 25 | 27–30 |
| август | 1, 8, 15, 22, 29 | 31–35 |
| сентябрь | 5, 12, 19, 26 | 36–39 |
| Октябрь | 3, 10, 17, 24, 31 | 40–44 |
| Ноябрь | 7, 14, 21, 28 | 45–48 |
| Декабрь | 5, 12, 19, 26 | 49–52 |
Компьютерная формула якорного дня в году
Для использования компьютера удобны следующие формулы для дня привязки в году.
Для григорианского календаря:
Для юлианского календаря:
якорь день знак равно Воскресенье + у + ⌊ у 4 ⌋ знак равно Воскресенье + 5 × ( у мод 4 ) + 3 × ( у мод 7 ) <\ displaystyle <\ mbox
400-летний цикл якорных дней
| Юлианские века | -1600J -900J -200J 500J 1200J 1900J 2600J 3300J | -1500J -800J -100J 600J 1300J 2000J 2700J 3400J | -1400J -700J 0J 700J 1400J 2100J 2800J 3500J | -1300J -600J 100J 800J 1500J 2200J 2900J 3600J | -1200J -500J 200J 900J 1600J 2300J 3000J 3700J | -1100J -400J 300J 1000J 1700J 2400J 3100J 3800J | -1000 Дж -300 Дж 400 Дж 1100 Дж 1800 Дж 2500 Дж 3200 Дж 3900 Дж | |||
|---|---|---|---|---|---|---|---|---|---|---|
| -1600 -1200 -800 -400 0 400 800 1200 1600 2000 2400 2800 3200 3600 | -1500 -1100 -700 -300 100 500 900 1 300 1700 2100 2500 2900 3300 3700 | -1400 -1000 -600 -200 200 600 1000 1400 1800 2200 2600 3000 3400 3800 | -1300 -900 -500 -100 300 700 1100 1500 1900 2300 2700 3100 3500 3900 | |||||||
| 00 | 28 год | 56 | 84 | Вт. | Пн. | Солнце. | Суббота. | Пт. | Чт. | Мы б. |
| 01 | 29 | 57 год | 85 | Мы б. | Вт. | Пн. | Солнце. | Суббота. | Пт. | Чт. |
| 02 | 30 | 58 | 86 | Чт. | Мы б. | Вт. | Пн. | Солнце. | Суббота. | Пт. |
| 03 | 31 год | 59 | 87 | Пт. | Чт. | Мы б. | Вт. | Пн. | Солнце. | Суббота. |
| 04 | 32 | 60 | 88 | Солнце. | Суббота. | Пт. | Чт. | Мы б. | Вт. | Пн. |
| 05 | 33 | 61 | 89 | Пн. | Солнце. | Суббота. | Пт. | Чт. | Мы б. | Вт. |
| 06 | 34 | 62 | 90 | Вт. | Пн. | Солнце. | Суббота. | Пт. | Чт. | Мы б. |
| 07 | 35 год | 63 | 91 | Мы б. | Вт. | Пн. | Солнце. | Суббота. | Пт. | Чт. |
| 08 | 36 | 64 | 92 | Пт. | Чт. | Мы б. | Вт. | Пн. | Солнце. | Суббота. |
| 09 | 37 | 65 | 93 | Суббота. | Пт. | Чт. | Мы б. | Вт. | Пн. | Солнце. |
| 10 | 38 | 66 | 94 | Солнце. | Суббота. | Пт. | Чт. | Мы б. | Вт. | Пн. |
| 11 | 39 | 67 | 95 | Пн. | Солнце. | Суббота. | Пт. | Чт. | Мы б. | Вт. |
| 12 | 40 | 68 | 96 | Мы б. | Вт. | Пн. | Солнце. | Суббота. | Пт. | Чт. |
| 13 | 41 год | 69 | 97 | Чт. | Мы б. | Вт. | Пн. | Солнце. | Суббота. | Пт. |
| 14 | 42 | 70 | 98 | Пт. | Чт. | Мы б. | Вт. | Пн. | Солнце. | Суббота. |
| 15 | 43 год | 71 | 99 | Суббота. | Пт. | Чт. | Мы б. | Вт. | Пн. | Солнце. |
| 16 | 44 год | 72 | Пн. | Солнце. | Суббота. | Пт. | Чт. | Мы б. | Вт. | |
| 17 | 45 | 73 | Вт. | Пн. | Солнце. | Суббота. | Пт. | Чт. | Мы б. | |
| 18 | 46 | 74 | Мы б. | Вт. | Пн. | Солнце. | Суббота. | Пт. | Чт. | |
| 19 | 47 | 75 | Чт. | Мы б. | Вт. | Пн. | Солнце. | Суббота. | Пт. | |
| 20 | 48 | 76 | Суббота. | Пт. | Чт. | Мы б. | Вт. | Пн. | Солнце. | |
| 21 год | 49 | 77 | Солнце. | Суббота. | Пт. | Чт. | Мы б. | Вт. | Пн. | |
| 22 | 50 | 78 | Пн. | Солнце. | Суббота. | Пт. | Чт. | Мы б. | Вт. | |
| 23 | 51 | 79 | Вт. | Пн. | Солнце. | Суббота. | Пт. | Чт. | Мы б. | |
| 24 | 52 | 80 | Чт. | Мы б. | Вт. | Пн. | Солнце. | Суббота. | Пт. | |
| 25 | 53 | 81 год | Пт. | Чт. | Мы б. | Вт. | Пн. | Солнце. | Суббота. | |
| 26 | 54 | 82 | Суббота. | Пт. | Чт. | Мы б. | Вт. | Пн. | Солнце. | |
| 27 | 55 | 83 | Солнце. | Суббота. | Пт. | Чт. | Мы б. | Вт. | Пн. | |
Поскольку в григорианском календаре 146097 дней, или ровно 20871 семидневная неделя, в 400 лет день якоря повторяется каждые четыре столетия. Например, день привязки 1700–1799 совпадает с днем привязки 2100–2199, то есть в воскресенье.
| Воскресенье | понедельник | вторник | среда | четверг | Пятница | Суббота | Всего | |
|---|---|---|---|---|---|---|---|---|
| Невисокосные годы | 43 год | 43 год | 43 год | 43 год | 44 год | 43 год | 44 год | 303 |
| Високосные годы | 13 | 15 | 13 | 15 | 13 | 14 | 14 | 97 |
| Всего | 56 | 58 | 56 | 58 | 57 год | 57 год | 58 | 400 |
Частота появления определенной даты в конкретный будний день может быть легко выведена из вышеизложенного (для даты с 1 января по 28 февраля соотнесите ее с концом света предыдущего года).
28-летний цикл
Что касается частоты Судных дней в 28-летнем цикле по юлианскому календарю, то для каждого дня недели есть 1 високосный год и 3 обычных года, последние через 6, 17 и 23 года после первого (то есть с интервалами в 6, 11, 6 и 5 лет). лет; распределяется неравномерно, потому что через 12 лет день пропускается в последовательности Судных дней). Тот же цикл применяется к любой дате, начиная с 1 марта, приходящегося на определенный будний день.
Таким образом, для любой даты, кроме 29 февраля, интервалы между обычными годами, приходящимися на конкретный будний день, равны 6, 11, 11. См., Например, внизу страницы Общий год, начинающийся в понедельник, годы в диапазоне 1906–2091.
29 февраля, приходящееся на определенный будний день, бывает только один раз в 28 лет, и это, конечно, високосный год.
Юлианский календарь
Обратите внимание, что григорианский календарь не был принят одновременно во всех странах, поэтому на протяжении многих веков в разных регионах использовались разные даты для одного и того же дня.