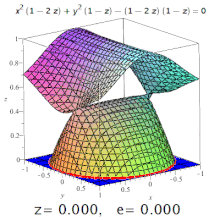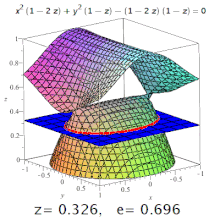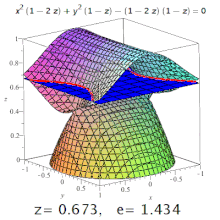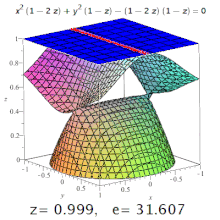
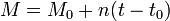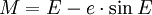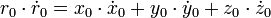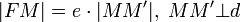Чем больше эксцентриситет тем больше
Эксцентриситет орбиты
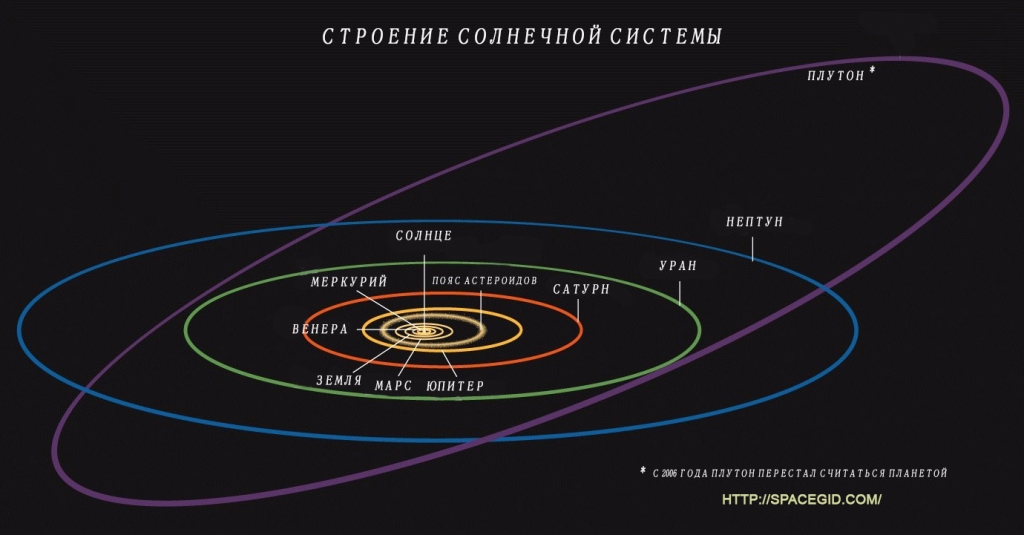
Строение Солнечной системы
Эксцентриситет (обозначается e или ε) входит в шестёрку кеплеровских элементов орбиты. Наряду с большой полуосью он определяют форму орбиты.
Определение эксцентриситета
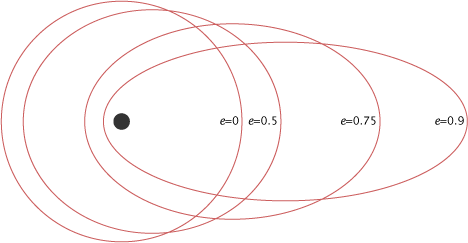
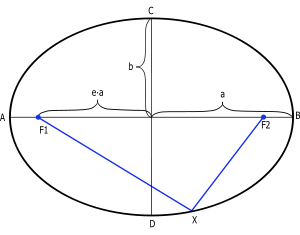
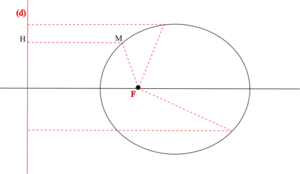
Первый закон Кеплера гласит о том, что орбиты любой планеты Солнечной системы представляет собой эллипс. Эксцентриситет определяет, насколько орбита отлична от окружности. Он равен отношению расстояния от центра эллипса (c) до его фокуса большой полуоси (a).
Эксцентриситеты объектов Солнечной Системы
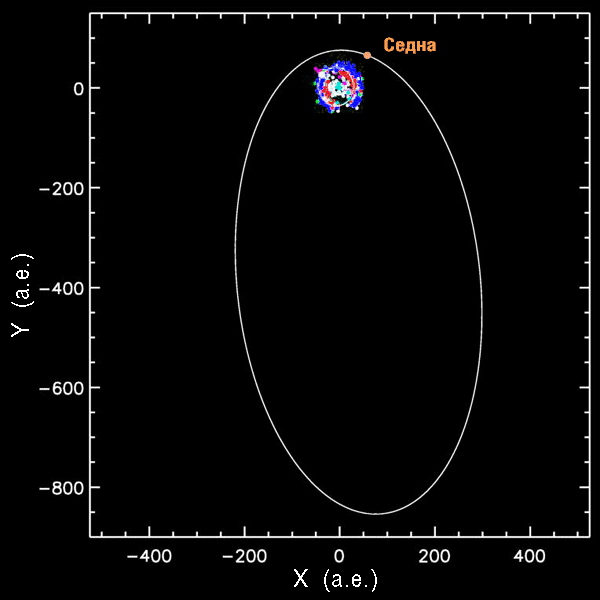
Орбита Седны. В центре координат — Солнечная система, окруженная роем планет и известных объектов пояса Койпера.
В нашей системе орбиты планет ничем не примечательны. Самой «круговой» орбитой обладает Венера. Её афелий всего-лишь на 1,4 млн. км.больше перигелия, а эксцентриситет равен 0,007 (у Земли – 0,016). По довольно вытянутой орбите движется Плутон. Обладая ε = 0,244, он временами приближается к Солнцу даже ближе чем Нептун. Однако, поскольку Плутон не так давно попал в разряд карликовых планет, самую вытянутую орбит среди планет теперь имеет Меркурий, обладающий ε = 0,204.
Среди карликовых планет наиболее примечательна Седна. Обладая ε = 0,86, она делает полный оборот вокруг Солнца почти за 12 тысяч лет, удаляясь от неё в афелии более чем на тысячу астрономический единиц. Однако даже это несравнимо с параметрами орбит долгопериодических комет. Периоды их обращения порой исчисляются миллионами лет, а многих из них и вовсе никогда не вернутся к Солнцу – т.е. обладают эксцентриситетом, большем 1. Облако Оорта может содержать триллионы комет, удалённых от Солнца на 50-100 тысяч астрономических единиц (0,5 – 1 световых лет). На таких расстояниях на нихмогут влиять другие звёзды и галактические приливные силы. Поэтому такие кометы могут обладать очень непредсказуемыми и непостоянными орбитами с самими различными эксцентриситетами.
Наконец, самым интересным является то, что даже Солнце обладает совсем ни круговой орбитой, как это может показаться на первый взгляд. Как известно, Солнце движется вокруг центра Галактики, проделывая свой путь за 223 млн. лет. Причём, из-за бесчисленного взаимодействия со звездами она получила довольно ощутимый эксцентриситет, равный 0,36.
Эксцентриситеты в других системах
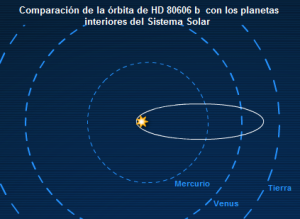
Сравнение орбиты HD 80606 b с внутренними планетами Солнечной системы
Открытие других солнечных систем неизбежно влечёт открытие планет с очень причудливыми параметрами орбит. Примером тому служат эксцентричные юпитеры, газовые гиганты с довольно высокими эксцентриситетами. В системах, имеющие такие планеты невозможно существование планет, подобных Земле. Они неизбежно упадут на гиганты или же статут их спутниками.
Среди обнаруженных на данный момент эксцентричных юпитеров самым большим эксцентриситетом обладает HD 80606b. Он движется вокруг звезды чуть меньшей, чем наше Солнце. Эта планета в перигелии приближается к звезде в 10 раз ближе, чем Меркурий к Солнцу, тогда как в афелии она удаляется от неё почти на астрономическую единицу. Таким образом, она имеет эксцентриситет 0,933.
Стоит отметить, что хоть данная планета и пересекает зону жизни, ни о каких видах привычной биосферы не может идти и речи. Её орбита создаёт на планете экстремальный климат.За короткий период сближения со звездой температура её атмосферы за считанные часы меняется на сотни градусов, в результате чего скорость ветров достигают многих километров в секунду. Подобными условиями обладают прочие планеты с высокими коэффициентами. Тот же Плутон, к примеру, при приближение к Солнцу приобретает обширную атмосферу, которая оседает в виде снега при удалении. В тоже время все Землеподобные планеты обладают орбитами, близкими к круговым. Поэтому эксцентриситет можно назвать одним из параметров, определяющим возможность наличия органической жизни на планете.
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Более формально два конических участка подобны тогда и только тогда, когда они имеют одинаковый эксцентриситет.
Можно представить себе эксцентриситет как меру того, насколько коническое сечение отклоняется от круглого. В частности:
СОДЕРЖАНИЕ
Определения
Эксцентриситет также можно определить в терминах пересечения плоскости и конуса с двойным ворсом, связанного с коническим сечением. Если конус ориентирован так, чтобы его ось была вертикальной, эксцентриситет равен
Альтернативные названия
Обозначение
Обычно используются три условных обозначения:
В этой статье используются первые обозначения.
Значения
Когда коническое сечение задано в общей квадратичной форме
Эллипсы
Эксцентриситет эллипса строго меньше 1. Когда круги (с эксцентриситетом 0) считаются эллипсами, эксцентриситет эллипса больше или равен 0; если окружности отнесены к особой категории и исключены из категории эллипсов, то эксцентриситет эллипса строго больше 0.
Мы определяем ряд связанных дополнительных понятий (только для эллипсов):
Другие формулы эксцентриситета эллипса
Определить максимальный и минимальный радиусы и как максимальные и минимальные расстояния от любого фокуса к эллипсу (то есть расстояние от фокуса либо к двум концам главной оси). Тогда для большой полуоси a эксцентриситет определяется выражением р Максимум <\ displaystyle r _ <\ text 
р мин <\ displaystyle r _ <\ text
это расстояние между фокусами, деленное на длину большой оси.
Гиперболы
Квадрики
Небесная механика
Аналогичные классификации
В ряде математических классификаций используется терминология, полученная из классификации конических сечений по эксцентриситету:
Эксцентриситет
Эксцентрисите́т — числовая характеристика конического сечения, показывающая степень его отклонения от окружности. Обычно обозначается “
” или “
”.
Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия.
Содержание
Определение
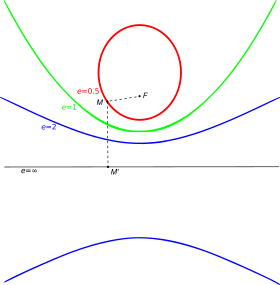
Все невырожденные конические сечения, кроме окружности, можно описать следующим способом:
Выберем на плоскости точку 
и прямую 
и зададим вещественное число 
0″ border=»0″ />. Тогда геометрическое место точек 
, для которых отношение расстояний до точки и до прямой равно раз, является коническим сечением. То есть, если 
есть проекция на то
Связанные определения
Свойства
Литература
Полезное
Смотреть что такое «Эксцентриситет» в других словарях:
ЭКСЦЕНТРИСИТЕТ — (обозначение е), один из элементов орбиты. Указывает, насколько эллиптическая ОРБИТА небесного тела отличается от круговой. Эксцентриситет вычисляют, разделив расстояние между двумя фокусами эллипса на длину главной оси. Эксцентриситет круга… … Научно-технический энциклопедический словарь
ЭКСЦЕНТРИСИТЕТ — орбиты один из элементов орбиты небесных светил, характеризующий ее форму. Птолемей первый использовал термин для описания орбит планет вокруг Солнца, рассматривая Землю как центральную точку наблюдения. Он исходил из двух допущений: первое, что… … Астрологическая энциклопедия
эксцентриситет — эллиптичность; расстояние, эксцентрицитет Словарь русских синонимов. эксцентриситет сущ., кол во синонимов: 3 • дезаксиал (1) • … Словарь синонимов
ЭКСЦЕНТРИСИТЕТ — число, равное отношению расстояния от любой точки кривой 2 го порядка до (см.) к расстоянию от этой точки до соответствующей (см.). Эксцентриситет окружности равен нулю, эллипса меньше единицы, параболы равен единице, гиперболы больше единицы … Большая политехническая энциклопедия
ЭКСЦЕНТРИСИТЕТ — конического сечения число, равное отношению расстояния от точки конического сечения до фокуса к расстоянию от этой точки до соответствующей директрисы … Большой Энциклопедический словарь
ЭКСЦЕНТРИСИТЕТ — в технике см. Эксцентрик … Большой Энциклопедический словарь
эксцентриситет — I конического сечения, число, равное отношению расстояния от точки конического сечения до фокуса к расстоянию от этой точки до соответствующей директрисы. II в технике, см. Эксцентрик … Энциклопедический словарь
ЭКСЦЕНТРИСИТЕТ — (Eccentricity) расстояние от центра эксцентрика до центра вала. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
ЭКСЦЕНТРИСИТЕТ — 1) расстояние между центром вращающейся оси и центром диска эксцентрика, насаженного на эту ось; 2) расстояние между направлением силы, приложенной к телу, и осью, проходящей через центры тяжести поперечных сечений тела. В таком случае говорят,… … Технический железнодорожный словарь
эксцентриситет — В сопротивлении материалов расстояние от центра тяжести сечения бруса до точки приложения равнодействующей сжимающих или растягивающих сил [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики строительная… … Справочник технического переводчика
Эксцентриситет орбиты
Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве в задаче двух тел:
Первые два определяют форму орбиты, третий, четвёртый и пятый — ориентацию по отношению к базовой системе координат, шестой — положение тела на орбите.
Содержание
Большая полуось
Большая полуось — это половина главной оси эллипса | AB | (обозначена на рис.2 как a ). В астрономии характеризует среднее расстояние небесного тела от фокуса
Эксцентриситет
Эксцентрисите́т (обозначается « e » или «ε») — числовая характеристика конического сечения. Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия. [1] Эксцентриситет характеризует «сжатость» орбиты. Он выражается по формуле:
, где b — малая полуось (см. рис.2)
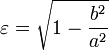
Можно разделить внешний вид орбиты на пять групп:
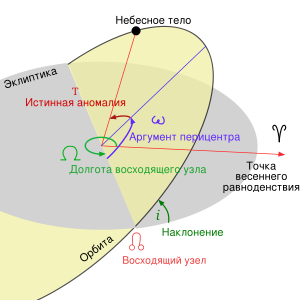
Наклонение
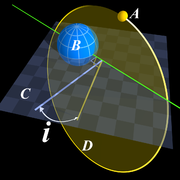
Наклонение орбиты (накло́н орбиты, накло́нность орбиты, наклоне́ние) небесного тела — это угол между плоскостью его орбиты и плоскостью отсчёта (базовой плоскостью).
Обычно обозначается буквой i (от англ. inclination ). Наклонение измеряется в угловых градусах, минутах и секундах.
Аргумент перицентра
Аргуме́нт перице́нтра — определяется как угол между направлениями из притягивающего центра на восходящий узел орбиты и на перицентр (ближайшую к притягивающему центру точку орбиты спутника), или угол между линией узлов и линией апсид. Отсчитывается из притягивающего центра в направлении движения спутника, обычно выбирается в пределах 0°-360°. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидов вокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д.
При исследовании экзопланет и двойных звёзд в качестве базовой используют картинную плоскость — плоскость, проходящую через звезду и перпендикулярную лучу наблюдения звезды с Земли. Орбита экзопланеты, в общем случае случайным образом ориентированная относительно наблюдателя, пересекает эту плоскость в двух точках. Точка, где планета пересекает картинную плоскость, приближаясь к наблюдателю, считается восходящим узлом орбиты, а точка, где планета пересекает картинную плоскость, удаляясь от наблюдателя, считается нисходящим узлом. В этом случае аргумент перицентра отсчитывается из притягивающего центра против часовой стрелки.
Обозначается (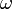
).
Долгота восходящего узла
Долгота́ восходя́щего узла́ — один из основных элементов орбиты, используемых для математического описания формы орбиты и её ориентации в пространстве. Определяет точку, в которой орбита пересекает основную плоскость в направлении с юга на север. Для тел, обращающихся вокруг Солнца, основная плоскость — эклиптика, а нулевая точка — Первая точка Овна (точка весеннего равноденствия).
Обозначается ☊ или Ω.
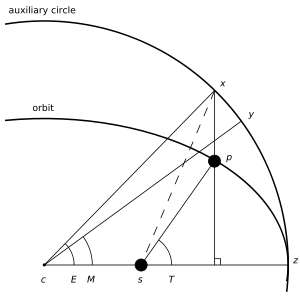
Средняя аномалия
Средняя аномалия для тела, движущегося по невозмущённой орбите — произведение его среднего движения и интервала времени после прохождения перицентра. Таким образом, средняя аномалия есть угловое расстояние от перицентра гипотетического тела, движущегося с постоянной угловой скоростью, равной среднему движению.
Обозначается буквой M (от англ. mean anomaly )
В звёздной динамике средняя аномалия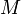 
вычисляется по следующим формулам:
Вычисление кеплеровых элементов
Прежде всего, вычислим большую полуось:
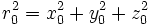
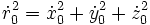
По интегралу энергии:
(1) 
, где k — гравитационный параметр равный произведению гравитационной постоянной на массу небесного тела, для Земли K = 3,986005×10 5 км³/c², для Солнца K = 1,32712438×10 11 км³/c².
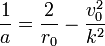
Эксцентриситет (математика)
Эксцентрисите́т (обозначается “ e ” или “ε”) — числовая характеристика конического сечения, показывающая степень его отклонения от окружности.
Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия.
Определение
Все невырожденные конические сечения, кроме окружности, можно описать следующим способом:
В зависимости от эксцентриситета, получится:
Другие определения
Так же для эллипса и гиперболы эксцентриситет ещё можно определить как отношение расстояний между фокусами к большей или действительной оси.
Литература
Полезное
Смотреть что такое «Эксцентриситет (математика)» в других словарях:
Гипербола (математика) — У этого термина существуют и другие значения, см. Гипербола. Гипербола и её фокусы … Википедия
Коническое сечение — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса) … Википедия
Конические сечения — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия
Фокус (в математике) — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия
Эллипс — Не следует путать с Эллипсис. Эллипс, его фокусы и главные оси … Википедия
Малая полуось — Не следует путать с термином «Эллипсис». Эллипс и его фокусы Эллипс (др. греч. ἔλλειψις недостаток, в смысле недостатка эксцентриситета до 1) геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1… … Википедия
Эллипс (геометрич.) — Не следует путать с термином «Эллипсис». Эллипс и его фокусы Эллипс (др. греч. ἔλλειψις недостаток, в смысле недостатка эксцентриситета до 1) геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1… … Википедия
Гиппарх — Для этой статьи не заполнен шаблон карточка. Вы можете помочь проекту, добавив его … Википедия
Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия
Астрономия — (от греческих слов άστρον, светило, и νόμος, закон) наука о небесных светилах. В обширном значении этого слова А. включает в себе исследование всего того, что можно знать о небесных светилах: солнце, луне, планетах, кометах, падающих звездах,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона