Чем больше коэффициент шарпа тем
Коэффициент Шарпа
Коэффициент Шарпа, как и альфа, оценивает труд управляющего. Только сравнивает доходность портфеля не с движением какого-либо эталона, а с колебанием доходности самого портфеля за анализируемый период. Т.е. дается «внутренняя» оценка «качества» доходности портфеля, без использования «внешних» данных. Другими словами, дается абсолютная, а не относительная оценка полученной за период доходности.
• R — доходность портфеля (актива)
• Rf — доходность от альтернативного вложения
• σ — стандартное отклонение доходности портфеля (актива)
Колебания доходности — это риск. Высокие колебания — это высокий риск, и они должны приносить высокий доход. Колебания доходности измеряются стандартным отклонением, которое помещается в знаменатель дроби, рассчитывающей коэффициент Шарпа. В числителе дроби – доходность портфеля, очищенная от гарантированной рыночной доходности — от доходности безрискового вложения, в качестве которого, как правило, берется депозит в Сбербанке.
Если портфель показал доходность 30% со стандартным отклонением равным 10, а депозит Сбербанка принес бы 12%, то коэффициент Шарпа будет равен (30-12)/10 = 1,8. Можно сказать, что за каждую единицу риска были получены 1,8 единиц доходности сверх гарантированной безрисковой доходности.
Чем значение коэффициента Шарпа выше, тем выгоднее управляющий использует риск портфеля. Причем, благодаря тому, что этот коэффициент использует стандартное отклонение доходности самого портфеля, а не внешний эталон, он может быть применен для сравнения между собой различный портфелей.
При одинаковой доходности портфели могут иметь разные значения этого коэффициента, потому что они принимают на себя разное количество риска. Портфель, у которого коэффициент Шарпа выше при одинаковой доходности, достиг результата с меньшим риском. Чем выше стандартное отклонение, тем больше знаменатель уравнения коэффициента Шарпа, а значит портфелю нужно показывать высокую доходность, чтобы заработать высокое значение этого показателя. Портфелю с низким уровнем риска (небольшим стандартным отклонением) достаточно показывать умеренную доходность, чтобы его коэффициент Шарпа был достаточно высоким.
У коэффициента Шарпа есть преимущество перед альфой. Стандартное отклонение измеряет волатильность фонда в абсолютной величине, а не относительной, как альфа. Поэтому, если для полезности альфы должен быть высоким коэффициент корреляции, то коэффициент Шарпа всегда имеет полноценное значение, независимо от других показателей.
Как выбрать портфель по соотношению доходности и риска
Перед тем как начать читать: данный материал насыщен формулами, которые не всегда легки для восприятия. Однако мы никак не смогли обойтись без них, описывая данный метод анализа.
Любой инвестор желает составить такой портфель акций, который будет обгонять рынок по доходности на длинной дистанции. Но он должен учитывать, что высокая доходность напрямую связана с рисками более высоких потерь. Поэтому при создании портфеля необходимо учитывать оба параметра — доходность и риск.
В классическом варианте риск равен волатильности доходности, которая рассчитывается как стандартное отклонение доходности портфеля:
При одинаковой доходности акции с меньшей волатильностью характеризуются более стабильным ростом. То есть на графике цены мы увидим меньше резких импульсов вверх или вниз. Это и является мерой риска. При неблагоприятной рыночной обстановке бумаги с высокой волатильностью могут сильно обрушиться. Чтобы им вырасти до начальных значений, придется показать сравнительно больший прирост в процентах. Например, если акция упала на 20%, то для возврата к исходному уровню ей необходимо подняться уже на 25%.
Для оценки привлекательности портфеля существует множество показателей. Например, бета отражает на сколько процентов изменится стоимость портфеля при изменении рынка на 1%. Коэффициент показывает волатильность бумаг в портфеле по отношению к рынку в целом и характер зависимости (прямой или обратный).
Коэффициент альфа Йенсена демонстрирует, насколько портфель акций обгоняет свою теоретическую доходность. По сути он показывает, насколько портфель «обыгрывает» рынок за счет рационального составления, исключая влияние волатильности.
Подробнее об этих коэффициентах читайте в материалах:
Но данные показатели не отражают эффективность портфелей, которая должна учитывать не только риск (бета) или доходность (альфа Йенсена), а сразу оба параметра. Для этого были придуманы специальные коэффициенты.
Коэффициент Шарпа
Коэффициент Шарпа (Sharp ratio) — один из самых популярных инструментов для оценки эффективности портфеля. Формула:
В качестве безрискового актива может выступать ключевая ставка Центрального Банка, процент по депозитам наиболее надежных банков или доходность государственных облигаций.
Разница между средней доходностью портфеля и средней доходностью безрискового актива показывает, насколько портфель обгоняет «гарантированную» доходность. Стандартное отклонение в знаменателе формулы отражает риск портфеля. Чем выше коэффициент, тем более привлекателен портфель.
Как правило, коэффициент Шарпа используют для сравнения разных портфелей. Но в целом диапазон значений можно разделить на три группы:
1. Sharp ratio меньше нуля. Вложения невыгодны, поскольку приносят меньший доход по сравнению с безрисковым активом.
2. Sharp ratio находится в диапазоне от 0 до 1. Уровень риска достаточно высок для соответствующей доходности.
3. Sharp ratio больше единицы. Уровень риска по отношению к доходности является комфортным.
Коэффициент Сортино
Данный коэффициент по сути является преобразованным коэффициентом Шарпа. Его формула отличается тем, что стандартное отклонение в знаменателе рассчитывается только для отрицательных значений, то есть только для убыточных периодов.
Таким образом, риск в формуле исключает колебания стоимости портфеля в благоприятные периоды времени. Это позволяет подойти к оценке риск-профиля портфеля более детально. Но нужно понимать, что в отдельных случаях такой подход может «замаскировать» активы с повышенным риском.
Коэффициент Трейнора
Коэффициент Трейнора по аналогии с предыдущими отражает соотношение доходность/риск. В качестве оценки риска берется коэффициент бета, упомянутый в начале статьи. Напомним, что бета отражает волатильность портфеля по отношению к рынку.
Формула коэффициента Трейнора:
Коэффициент Трейнора отражает превышение «чистой» доходности (т.е. за вычетом безрисковой ставки) над систематическим риском* (бета). В этом его основное отличие от коэффициентов Шарпа и Сортино.
* Рыночный риск, который нельзя устранить при помощи диверсификации активов
В общем случае значения коэффициента Трейнора ниже нуля указывают на то, что целесообразнее инвестировать в рыночный индекс, так как портфель проигрывает по соотношению доходность/риск. При положительных значениях портфель показывает себя лучше рынка, и вложения в него считаются привлекательными.
Коэффициент Модильяни
Показатель Модильяни (M2) рассчитывается как коэффициент Шарпа, умноженный на стандартное отклонение доходности рынка, плюс безрисковая ставка доходности. Поскольку показатель Модильяни получен путем линейных преобразований показателя Шарпа, то для сравнения разных портфелей будет достаточного одного из этих коэффициентов (М2 или Шарпа). Рейтинг портфелей будет идентичный. Формула:
Коэффициент Модильяни наглядно показывает на какую доходность мог бы рассчитывать инвестор при условии, что риск портфеля равен рыночному.
Коэффициент Швагера
Показатель Швагера находится путем деления среднемесячной прибыли портфеля (доходность) на среднее значение максимальной просадки за каждый месяц (риск). Полученное значение берется в виде абсолютной величины. Все просто: чем больше коэффициент, тем привлекательней портфель.
Показатель позволяет оперативно сравнить несколько портфелей по соотношению риск/доходность. Минимальный рекомендуемый период для расчета коэффициента — 12 месяцев.
Составляем портфели
В качестве наглядного примера рассчитаем все вышеописанные коэффициенты для двух разных портфелей. Структуры портфелей и доли составлялись случайным образом.
Для расчета показателей мы взяли период с января 2018 г. по июль 2019 г. Шаг выборки — 1 месяц. Таким образом размер выборки для оценки доходности портфеля составил 19.
В качестве рыночного бенчмарка мы взяли Индекс МосБиржи полной доходности, который включает в себя выплаты дивидендов с их реинвестированием. Для корректного сравнения индекса с портфелями доходность каждой бумаги рассчитывалась также с учетом дивидендов.
Риск каждого набора ценных бумаг отражает стандартное отклонение доходности. У индекса и первого портфеля оно отличается незначительно — менее чем на 0,5% (в месяц). Самый высокий «риск» имеет второй портфель. Но что касается стандартного отклонения, которое рассчитывается исключительно по убыточным периодам, последний портфель показал лучший результат (наименее рисковый).
Первый портфель обгоняет индекс по показателям Шарпа и Сортино. Проще говоря, демонстрирует более высокую доходность к риску. Второй портфель незначительно уступает бенчмарку только по коэффициенту Шарпа, но существенно обгоняет по Сортино. Расчет оставшихся показателей (Бета, Трейнора, Модильяни) для индекса будет некорректным из-за того, что формулы подразумевают сравнение с рынком.
Показатель Швагера не рассчитывался для первого портфеля из-за большого количества бумаг. Напомним, что для поиска средней максимальной просадки по портфелю необходимо выявить максимальные просадки по каждой бумаге за каждый месяц.
Таким образом, общий анализ коэффициентов показывает, что по сравнению с российским рынком акций в целом оба портфеля привлекательны для инвестирования. Выбор между двумя вариантами в данном случае зависит от предпочтений инвестора в специфике риска. Если важнее общий уровень риска, то привлекательнее первый портфель. Если нужно минимизировать риск только для убыточных периодов, то в сравнении с рынком подходят оба портфеля, но выигрывает второй вариант.
Заключение
Описанные коэффициенты могут быть крайне полезны для сравнения привлекательности:
— портфелей с разной структурой;
— портфелей с одним набором ценных бумаг, но разными весами.
При этом для получения максимальной информации о соотношении доходности к риску рекомендуется использовать несколько показателей. Однако нужно понимать, что мультипликаторы — не панацея. Анализ коэффициентов отлично дополняется фундаментальной оценкой активов в портфеле, техническим анализом и другими моделями оценки.
БКС Брокер
Последние новости
Рекомендованные новости
Главное за неделю. Будем качать посвистывая
Итоги торгов. Распродажи могут усилиться на следующей неделе
Идеальные фишки: дают максимум доходности на единицу риска
Наиболее подходящие акции США для активных трейдеров на декабрь
Внимание, Snap!
Агрегатор такси уезжает в Гонконг. Китайские бумаги поехали вниз!
Небольшой биотех потеснил Apple в топе по оборотам на СПБ Бирже
Адрес для вопросов и предложений по сайту: bcs-express@bcs.ru
* Материалы, представленные в данном разделе, не являются индивидуальными инвестиционными рекомендациями. Финансовые инструменты либо операции, упомянутые в данном разделе, могут не подходить Вам, не соответствовать Вашему инвестиционному профилю, финансовому положению, опыту инвестиций, знаниям, инвестиционным целям, отношению к риску и доходности. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «Компания БКС» не несет ответственности за возможные убытки инвестора в случае совершения операций, либо инвестирования в финансовые инструменты, упомянутые в данном разделе.
Информация не может рассматриваться как публичная оферта, предложение или приглашение приобрести, или продать какие-либо ценные бумаги, иные финансовые инструменты, совершить с ними сделки. Информация не может рассматриваться в качестве гарантий или обещаний в будущем доходности вложений, уровня риска, размера издержек, безубыточности инвестиций. Результат инвестирования в прошлом не определяет дохода в будущем. Не является рекламой ценных бумаг. Перед принятием инвестиционного решения Инвестору необходимо самостоятельно оценить экономические риски и выгоды, налоговые, юридические, бухгалтерские последствия заключения сделки, свою готовность и возможность принять такие риски. Клиент также несет расходы на оплату брокерских и депозитарных услуг, подачи поручений по телефону, иные расходы, подлежащие оплате клиентом. Полный список тарифов ООО «Компания БКС» приведен в приложении № 11 к Регламенту оказания услуг на рынке ценных бумаг ООО «Компания БКС». Перед совершением сделок вам также необходимо ознакомиться с: уведомлением о рисках, связанных с осуществлением операций на рынке ценных бумаг; информацией о рисках клиента, связанных с совершением сделок с неполным покрытием, возникновением непокрытых позиций, временно непокрытых позиций; заявлением, раскрывающим риски, связанные с проведением операций на рынке фьючерсных контрактов, форвардных контрактов и опционов; декларацией о рисках, связанных с приобретением иностранных ценных бумаг.
Приведенная информация и мнения составлены на основе публичных источников, которые признаны надежными, однако за достоверность предоставленной информации ООО «Компания БКС» ответственности не несёт. Приведенная информация и мнения формируются различными экспертами, в том числе независимыми, и мнение по одной и той же ситуации может кардинально различаться даже среди экспертов БКС. Принимая во внимание вышесказанное, не следует полагаться исключительно на представленные материалы в ущерб проведению независимого анализа. ООО «Компания БКС» и её аффилированные лица и сотрудники не несут ответственности за использование данной информации, за прямой или косвенный ущерб, наступивший вследствие использования данной информации, а также за ее достоверность.
Коэффициент Шарпа – оцениваем эффективность вашей стратегии
Добрейшего времени суток, товарищи Форекс трейдеры! Чаще при оценке стратегий на Forex трейдеры смотрят на доходность в процентах. Чем их больше – тем лучше, не так ли? Но % доходности сильно зависит от риска и не отражает эффективности системы. Так какой показатель использовать? Стандартом у финансовых аналитиков считается Коэффициент Шарпа, выведенный нобелевским лауреатом Уильямом Шарпом.
Ниже мы рассмотрим как рассчитать коэффициент Шарпа для оценки эффективности стратегии, разберемся что же он означает (многие умеют его считать, но не понимают его смысла), а также сделаем выводы о том в каких случаях он полезен, а в каких нет.
Коэффициент Шарпа на Форекс
Коэффициент Шарпа придумал известный американский экономист – Уильям Шарп. На сегодня, это один из наиболее часто используемых показателей отношения риска к доходности. Еще большую значимость коэффициент приобрел, когда в 1990 году, за свою модель оценки финансовых активов (CAPM) Шарп был избран лауреатом Нобелевской премии.
Человеку из сферы финансов будет не сложно понять принцип расчета коэффициента Шарпа и что тот должен отображать. По сути, задача сводится к тому, чтобы узнать, сколько избыточной доходности вы получите в связи с удержанием более рискового актива. Думаю, не секрет, что лишний риск всегда должен сполна компенcироваться соответствующей доходностью. Чем больше значение коэффициента, тем больше прибыли на риск одной и той же суммы.
Формула расчета выглядит следующим образом:
Доходность актива
Доходность можно измерять с любой периодичностью – это может быть день, неделя, месяц, или год. Также, в качестве показателя доходности можно брать средний прирост на сделку. Единственное, желательно, чтобы исходные данные доходности должны быть нормально распределены. Отсюда и главная слабость коэффициента. Резкие пики на выборке в 3 и более стандартных отклонения и ассиметричное распределение (видимый наклон графика) могут стать причиной ложной оценки.
Безрисковый доход
Безрисковкый доход – это теоретический доход с нулевым риском. То есть, это та доходность, которую инвестор может получить абсолютно без риска за какой-то определенный период времени. По идее, – это минимальный доход, который инвестор ожидает получить от любой инвестиции. Сравнивая этот показатель с реальным доходом, можно определить, насколько хорошую компенсацию вы получаете за дополнительный риск.
На практике, понятия инвестиции с нулевым риском не существует, так как даже самые безопасные инвестиции несут с собой некоторую долю риска. Тем не менее, к безрисковой доходности можно отнести депозит в сбербанке, либо деньги, инвестированные в казначейские облигации США. Рынок форекс – это всегда инвестиции с высоким риском, поэтому безрисковая доходность в нашем случае будет равна нулю. Но, если ваш депозит хранится в банке, в формулу можно подставить значение текущей базовой ставки.
В терминале MT4 показатель Шарпа считается, как отношение среднеарифметической доходности сделки к стандартному отклонению, при нулевом значении безрисковой ставки.
Полная формула выглядит так:
Стандартное отклонение
Коэффициент Шарпа оценивает эффективность инвестиции с точки зрения дисперсии доходов. Так как мы уже подсчитали избыточную доходность (доходность за вычетом безрисковой ставки), осталось поделить это значение на стандартное отклонение доходности актива. То есть, посчитать отношение доходности к риску.
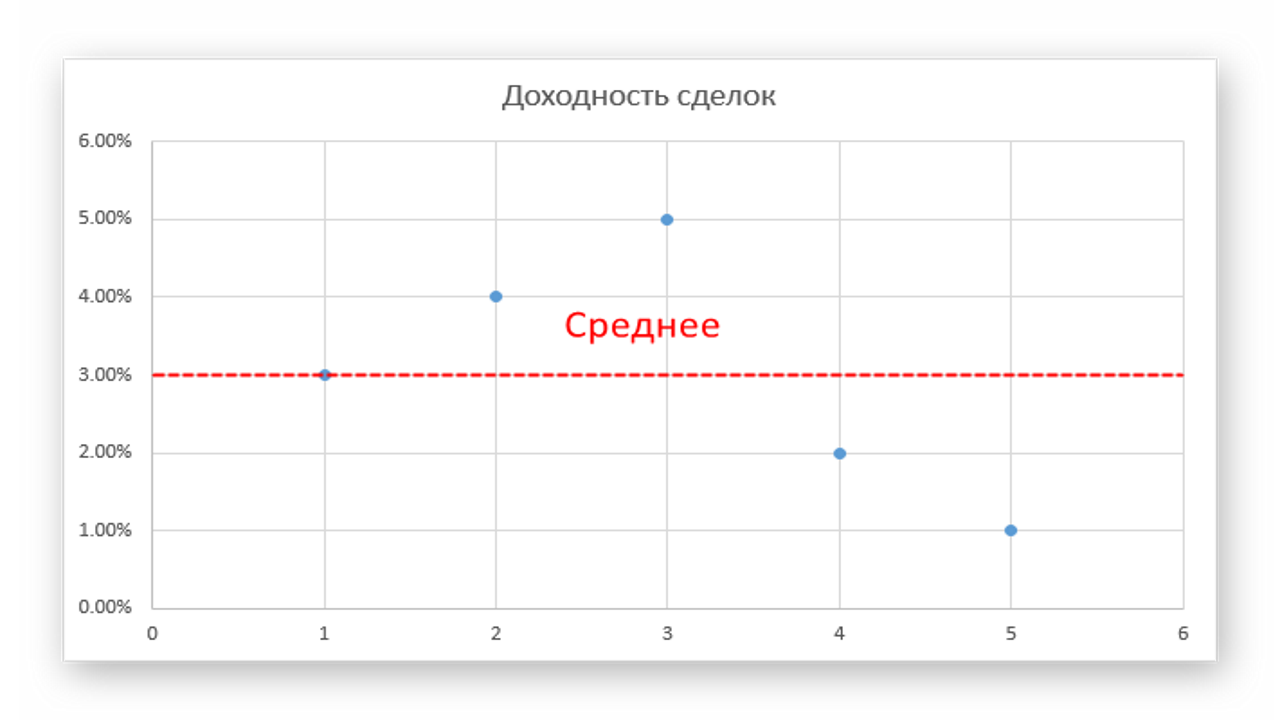
Далее, возводим значения в квадрат, получаем арифметическое среднее и выводим корень от результата – sqrt((0.00% + 0.01% + 0.04% + 0.01% + 0.04%) / 5) = 1.41%.
Для сравнения, возьмем немного другую выбрку: 2%, 8%, 5%, 4%, 6%. Очевидно, что доходность такой системы в рамках рассматриваемого периода больше, но мы также наблюдаем гораздо большую волатильность доходности, 2% против 1.41% у предыдущего примера. Соответственно, первая стратегия является менее рискованной.
Единицы расчёта коэффициента Шарпа
Для примера, попробуем сравнить эффективность двух торговых стратегий по показателям их доходности и риска. Допустим, первая стратегия дает 5% прибыли на сделку, при стандартном стандартном отклонении (показатель дисперсии доходности) равном 4%. Вторая стратегия в среднем приносит по 2% в каждой сделке, но отклонение не превышает 1%. В данном случае, первая стратегия будет иметь коэффициент шарпа 1.25, а вторая – 2.0. Это означает, что не смотря на меньшую доходность, вторая стратегия имеет лучшее соотношение риска к доходности.
Коэффициент Шарпа должен быть равен одному или выше. Тогда считается, что стратегия, которую мы анализируем, работает с достаточной эффективностью. Значение больше трех уже говорит о том, что вероятность получения убытка в каждой сделке меньше 1%. И чем больше полученное значение, тем лучше.
Вывод
В большинстве случаев, коэффициент Шарпа покажет реальную рентабельность стратегии. Но, иногда, показатель Шарпа может вводить в заблуждение. Например, некоторые облигации могут показывать стабильную доходность выше банковского процента в течении многих лет, на что коэффициент ответит нереалистично высокими показателями. В этом случае, полученное значение ничего не скажет о реальных рисках, стоящих за инвестированием в данную облигацию, пусть даже риск будет на самом деле минимальным. В целом же, данный коэффициент подойдёт для сравнения двух стратегий с относительно частыми входами и не самыми огромными целями.
Шарп и Сортино. Всё, что надо знать о этих коэффициентах.
Шарп и Сортино. Всё, что надо знать о этих коэффициентах.
Пояснение. В формуле рассчёта коэффициента Шарпа положительная доходность за период (например, за месяц) будет учитываться, как увеличение риска, что абсолютно нелогично.
В формуле рассчёта коэффициента Сортино увеличением риска считается падение доходности ниже установленного порога, т.е. все положительные и отрицательные значения доходностей за каждый период, которые ниже значения безрисковой ставки доходности.
Применение. Коэффициент Сортино удобно использовать для выбора ETF-ов в портфель.
В формуле рассчёта коэффициента Шарпа положительная доходность за период (например, за месяц) будет учитываться, как увеличение риска, что абсолютно нелогично.
Невозможно отличить высокодоходную систему с большой просадкой от низкодоходной с небольшой просадкой.
А разве они сильно отличаются? Если изменить размер плеча, они перетекут из одной в другую
Сберегатель (Сэр Лонг), можно тогда увеличить размер сделки, используемой в низкорисковой стратегии. Стратегия по проценту прироста капитала (и по просадке) станет близка к высокорисковой.
И, наоборот, уменьшить размер сделки в высокорисковой стратегии, значит снизить ее риски.
В общем, мне кажется, что необходимость видеть и различать высокорисковую стратегию с большой просадкой и низкорисковую стратегию с маленькой просадкой важна только, если у меня нет возможности никак изменить размер сделки, например я всегда захожу на 100% от депозита и не беру плечи. Конечно же, имхо.
можно тогда увеличить размер сделки, используемой в низкорисковой стратегии. Стратегия по проценту прироста капитала (и по просадке) станет близка к высокорисковой.
Нет, относительные значения не изменятся. Увеличатся только абсолютные значения.
С этим все же не соглашусь.
Пусть у нас будет стратегия А, где доходность составляет 40%, а просадка 20%. И стратегия Б, где доходность будет 20%, а просадка 10%.
Значит, используя в первом случае 50% от депозита, а во втором — 100%, я так и так получу 20% прибыли, имея при этом просадку в 10%.
Поэтому, с моей точки зрения, эти стратегии одинаковы, причем, что по относительным, что по абсолютным значениям.
Если изменить условия и в стратегии Б сделать просадку 5%, то стратегия Б станет приоритетной. Но, не забываем, что доходности и просадка прошлого не гарантируют, что в будущем будет также и вообще, это сферический пример в вакууме )
Сберегатель (Сэр Лонг), отклонение от среднего — это мера риска, неважно в какую сторону.
Опять же повторюсь — это зависит от того, что вкладывать в понятие риска. У классиков риск — это волатильность/СКО сами по себе. У Сортино — только просадка.
Сберегатель (Сэр Лонг), он не мусорный, он «другой» 🙂 Постараюсь пояснить.
Шарп в знаменателе имеет СКО всей выборки. Мы берём все результаты за некоторый период, находим среднюю и её колебания вверх-вниз, как бы коридор. Если поделить очищенную от безриска доходность на этот коридор, то мы как бы получаем нашу долю в этом коридоре, чем больше, тем лучше. Допущение: колебания цены вряд ли имеют нормальное распределение, но как бы все привыкли к такой трактовке, потому что другой нет.
Сортино делает в принципе то же самое, но берёт не всю выборку, а только значения ниже безриска, т.е. как бы делит взятое нами на фактически реализованный риск, а не весь потенциальный. Это точно так же далеко от идеала, как и Шарп 🙂 В инвестиционной теории любая доходность выше безриска имеет… риск, это её цена. Даже если риск (волатильность вниз в вашем контексте) не реализовался, он всё равно есть, и Сортино его упускает по сути. В принципе, он может никогда и не реализоваться, учитывая его случайный характер и ограниченность жизни фонда/трейдера.
Т.е. у нас либо допущение, что риск вверх = риск вниз, либо допущение, что если риск вниз не реализовался, то его можно не учитывать. В принципе, это шило на мыло, поэтому оба коэффициента живы до сих пор, ибо чистая вкусовщина 🙂
Даже если риск (волатильность вниз в вашем контексте) не реализовался, он всё равно есть, и Сортино его упускает по сути. В принципе, он может никогда и не реализоваться, учитывая его случайный характер и ограниченность жизни фонда/трейдера.
Реальность такова, что плохие варианты реализуются намного чаще, чем хорошие.
Поэтому дождаться волатильности вниз гораздо проще, чем волатильности вверх.
Я имею ввиду доходность системы, естественно.
Т.е. у Сортино есть огромная вероятность не упустить риск.
то в Сортине контртренд — всё, тренд — ничего.
svgr, разве нам не хватит того, что в результат (коэффициент) уже вшиты величина выигрыша, величина потерь и безрисковая ставка?
Сберегатель (Сэр Лонг), а откуда взялась величина выигрыша? От игры. Разве может быть неважным как этот выигрыш образовался? Равномерно или одномоментно. А Вы предлагаете эти случаи приравнять.
И случай Сортино = бесконечность какие практические выводы может дать? Бесполезен.
Не должно быть бесконечности.
А у Шарпа в этом случае волатильность есть, Вы рисковали, больше или меньше, и выиграли в результате. По Сортино в этом случае Вы не узнаете как Вы рисковали в процессе.
а откуда взялась величина выигрыша? От игры. Разве может быть неважным как этот выигрыш образовался? Равномерно или одномоментно. А Вы предлагаете эти случаи приравнять.
svgr, создание торговой системы или набора фильтров для портфеля — это творческий процесс.
И каждый реализует этот процесс в соответствии со своими индивидуальными потребностями.
Лично мне нравится Сортино и не нравится Шарп по указанным выше причинам.
Кроме того, эти коэффициенты дают фиксированный результат, который не нуждается в настройке.
И этот результат общедоступен, без дополнительных вычислений.
А кто может точно сказать, какие нужны веса для модифицированного коэффициента?
40/60 или 20/80?
Неизвестно.
А Вы предлагаете эти случаи приравнять.
Сберегатель (Сэр Лонг), эмпирика говорит что в определенных ситуациях вола эквивалентна рискам.
Вот мы держим позу овернайт — риск этой позы пропорционален воле рынка (долгосрочной и оцениваемой сейчас). Это точка зрения биржи при расчете ГО. А не оценка например рисков лонгов на аптренде отлично от оценки рисков шортов. Таки дела.
Это точка зрения биржи при расчете ГО.
В этом случае — да, Шарп уместен.
Ибо биржу в первую очередь заботят собственные риски.
А не риск того, что какая-то часть игроков внезапно разбогатеет.
Но в случае с трговыми системами и портфелями, будет абсурдным классифицировать позитивное явление (увеличение размера счёта) как событие, которое привносит риск.
Сберегатель (Сэр Лонг), биржу волнует платежеспособность игроков. Биржа считает что игрок который стоит в лонг овернайт несет плюс минус тот же риск что и игрок который стоит в шорт. Сортино отдает предпочтение тем кто угадал гэп. Типа нет убытка нет и риска. В 2008 году осенью словил гэп против тренда в ришке. Рынок внезапно закрылся (сообщение в квик пришло после того как) и открылся в другую сторону от того движения через несколько дней. Пока Сортино такое не словит он будет считать что все норм.
Не привносит а говорит о принимаемом риске. Если при росте индекса на 5% портфель дал +10% то это значит что в портфеле зашит риск относительно индекса. Если на движении рынка +50% кто то нажыл трехзнак то там левередж. А если там левередж то при гэпе против тренда мы получим гэп*левередж. Таки дела.
Сортино отдает предпочтение тем кто угадал гэп
Есть еще пара копеек которые следует добавить.
Шарп был разработан под лонговый портфель из акций без плеча (ну ладно, еще госбондов) и лажает уже даже с корп облигациями (волатильность ценового ряд отражает вероятность дефолта лучше чем доха что ле?), не говоря про деривативы и торговые стратегии. Как верно написано в статье Сортино предпочтительнее — какой нам толк от маловолатильно снижающейся еквити?
Сортино чуть получше но как и Шарп отображает только риски реализованные на участке бектеста.
Скажем etf на продажу краев/сеточное усреднение на аптренде фондового рынка может генерировать очень гладкую маловолатильную еквити годами и обосраться как слон за три сигмы. Трендовая может пройти по краю с зашкаливающим риском на трейд в каком нибудь декабре 2014 и не отразить его в еквити — привет тем кто считает необязательным управление размером позиций в зависимости от волы.
Да, можно сравнить две разных трендовых (контртрендовых, лонговых etf итд) между собой по Шарпу и Сортино. Но уже нельзя сравнить трендовую с контртрендовой, с лонгом сбера/микса на аптренде или там лонгом бакса. Сложно сравнить пиф на мусорные облиги с пифом госбондов — пока спокойно первый лучше, но риски то разные.
Вывод какой — считать надо, но надо понимать ограничения. Таки дела.
quant_trader, «Скажем etf на продажу краев/сеточное усреднение на аптренде фондового рынка может генерировать очень гладкую маловолатильную еквити годами и обосраться как слон за три сигмы»
Нужно считать не завершеннонные сделки.
а эквити как закрытие всех сделок прямо сейчас.
тогда все эти незакрытые убыточные сделки будут видны для коэффициента.
а так-же изменения цены опционов.
Антон Б, имел в виду нормальную переоценку открытых позиций а не форексные штучки. Покупка риска действительно может давать при нормальной переоценке маловолатильную (относительно доходности) эквити достаточно долго.
Торговля с плечом даже по тренду может иметь риски выше чем видны в еквити. Таки дела.
а эквити как закрытие всех сделок прямо сейчас.
Дмитрий Овчинников, краевые опционы по теор цене биржи. Мусорные облиги по цене маркетмейкера аффилянта. Всякие etf плечевые, брр. Ипотечные которые кино биг шорт.
Сортино чуть получше но как и Шарп отображает только риски реализованные на участке бектеста.
Сберегатель (Сэр Лонг), «Ну, а куда нам деваться от этого бэктеста?»
Включать здравый смысл, if then и прочее. Если мы без левереджа то где то можно обойтись бектестом, Шарпом и Сортино. Но мало ли etf с зашитым левереджем типа викса.
Мне давно давно писали что у гуру ДУ опционов (да не назову его имя чтобы не призвать его фанатов) загрузка по счету под завязку. Пофиг какая там эквити, при этом нормальный рисковик должен напрячься.
Если мы без левереджа то где то можно обойтись бектестом, Шарпом и Сортино. Но мало ли etf с зашитым левереджем типа викса.
Кстати vix нельзя торговать, как и любой индекс. Но в индексе ничего плохого нет, у него просто предназначение другое. А если б от викса пользы не было, его бы и не существовало вообще.
«Купить» VIX можно несколькими способами.
Лидером по оборотам является iPath® S&P 500 VIX Short-Term Futures ETN (VXX). Базируется на индексе, состоящем их краткосрочных фьючерсов на VIX. Для игре на росте волатильности бумаги необходимо купить.
Риски, связанные с этим продуктом таковы. Во-первых, волатильность базового актива, готовый способен двигаться по 10% в день и более, но в этом и заключается основная возможность сверхзаработка, связанная с подобный трейдом.
Во-вторых, динамика VXX может серьезно не совпадать с поведением VIX. Возможно запаздывание. Помимо этого, VXX не подходит для долгосрочной позиции, потому что фьючерсы на VIX обычно уменьшаются со временем. Это медленное снижение, вызванное потерями на перенос позиции перед экспирацией, происходит, когда фьючерс находится в контанго (дальние контракты выше ближних). Это обычно снижает цену на VXX на 5-10% за месяц.
Позитивный момент — несмотря на возможные расхождения с VIX, бумаги VXX отрицательно коррелируют с индексом S&P 500. Так что, при обвале широкого рынка вы сможете неплохо заработать на взлете подразумеваемой волатильности.
Данные за год, таймфрейм дневной
Ну и последнее, в теории ETN несут в себе риски контрагента. Для их создания сами фьючерсы на VIX управляющая компания не покупает, заключаются соответствующие свопы с банками. Для любителей бумаг ETF, лишенных риска контрагента, существует аналог — ProShares VIX Short-Term Futures ETF (VIXY). Тут торговые обороты и размер активов фонда в разы меньше.
Речь идет о продуктах c зашитым плечом. Они явно не для слабонервных, зато подходят для агрессивных интраждейщиков. Речь идет о маржинальных Exchange Traded Products. В настоящее время лучшим из них с точки зрения краткосрочного отслеживания динамики базового актива и ликвидности является ProShares Ultra VIX Short-Term Futures ETF (UVXY).
Продукт этот отслеживает колебания индекса S&P 500 VIX Short-Term Futures с двойным плечом. То есть при росте базового индекса на 1% UVXY прибавляет 2%, и наоборот. Как и в случае более консервативных вариантов, риски работы с UVXY связаны с неточным отражением бумагами динамики самого VIX. Ну, а возможность резких колебаний тут еще выше из-за левериджированности продукта.
Данные за год, таймфрейм дневной
Как вариант, возможна покупка самих фьючерсов на VIX. Это не самый удобный вариант, ибо фьючерсы необходимо заменять активными контрактами в преддверии экспирации. При этом, как показывает практика последних лет, долгожданного «золотого ключика» в виде взлета волатильности можно ждать месяцами.
Еще один способ — операции с опционами. Тут можно реализовывать более продвинутые, менее рисковые стратегии. Однако работа с опционами требуют неплохой предварительной подготовки, работа с ними сложнее, чем просто «покупка волатильности», которую предполагают ETF и т.п. Помимо этого, опционы на VIX частенько дороги из-за высокой волатильности базового актива.