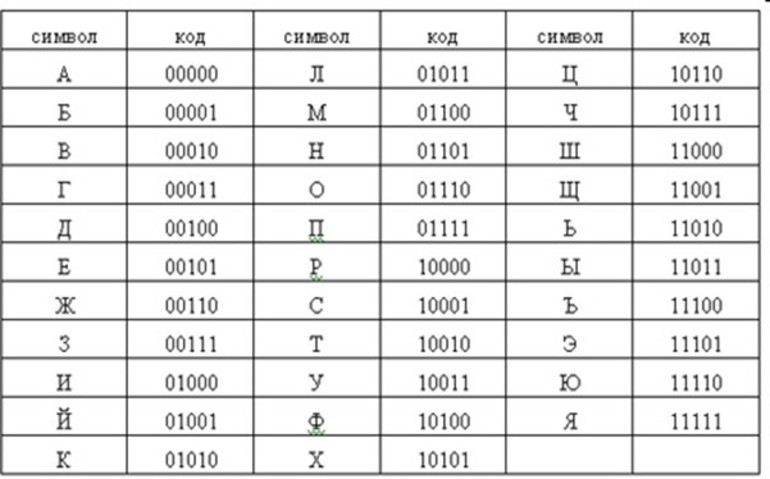
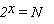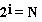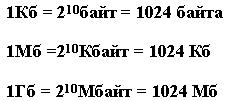Чем больше мощность алфавита тем больше количество информации

Мощность алфавита в информатике

Описание термина

Понятие мощности алфавита находится в основании изучения информатики. Алфавитом принято называть набор многочисленных символов. Сумма всех их в определённом языке и есть алфавитная мощность. Иными словами, это количество всех символов, входящих в конкретно взятый язык. Сюда входят не только буквы, но и прочие обозначения, в частности:

Это определение считается обобщённым и не принимает во внимание вычисления информационной составляющей сообщения. Она может содержать в себе числа, знаки препинания и прочее. В этом случае прибегают к использованию другого способа. Его суть основывается на том, что любая буква, цифра или знак обладают собственным информационным объемом данных. Компьютер работает с этим информационным кодом и распознает то, что было написано.

Основным постулатом в информатике является тот факт, что устройство разбирает введённую информацию исключительно в двоичном коде в форме нуля и единицы. В итоге получается, что абсолютно любой символ алфавита может быть успешно закодирован при помощи соответствующего подбора этих двух цифровых символов. Самая маленькая последовательность, применяемая при обозначении какой-либо цифры, буквы или другого знака, состоит из двух элементов.

Информационная масса отдельно взятого символа обычно изображается в форме информационной стандартной измерительной единицы, которая называется «бит». Восемь битов становятся равны одному байту.

Отображение символов в двоичном коде

Алфавитная мощность может быть использована на практике только при наличии двоичного кода. В качестве примера можно использовать упрощённый алфавит, состоящий всего из четырёх символов. В этом случае разрядность их и информационное представление описываются следующим образом:

Из этого списка можно сделать вывод о том, что если алфавитная мощность равняется 4, то масса отдельного единичного символа будет составлять 2 бита. Если же есть алфавит, состоящий из 8 символов, то при подборе двоичного трёхзначного кода для него комбинационное количество будет следующим:

Иными словами, если алфавитная мощность равна 8, то вес отдельно взятого символа для двоичного трёхзначного кода составит 3 бита.

Вычисление мощности алфавита

Эта формула была изобретена американским инженером Ральфом Хартли более сотни лет тому назад. Она применяется для работы с равновероятными событиями и используется для определения мощности конкретного буквенного набора, которая обозначается буквой N (информационная масса или объём). n означает численность бит в словесной единице, иными словами, количество знаков внутри двоичного кода. Так, если n равен 1, то N тоже равен 1, при n = 2 N = 4, при n = 3 N = 8, при n = 4 N = 16.

Чтобы сформулировать теорию о численности информации в набранном словосочетании, пользуются формулой I=K*i. В этом случае К обозначает численность всех символов в предложении, а i — это информационная масса символа.

При ответе на вопрос, как найти мощность алфавита, нужно сказать, что в русском языке 33 буквы, поэтому это можно выразить как N = 33. Для сравнения, аналогичный показатель в английском, немецком и французском языках равняется 26, в испанском — 27. Венгерский язык, например, является 40-символьным.

Существует также и клавиатурный язык, куда входят не только буквы, но и дополнительные знаки. Так, в русском языке есть ещё 10 цифр и 11 символов, а также пробел и пара скобок. Их мощность прибавляется к аналогичному буквенному показателю, и на выходе получается N = 33+10+11+1+2=57. В некоторых случаях букву «ё» не выделяют в качестве отдельного самостоятельного символа, и в таком случае полная мощность русского алфавита становится равна 56.

Определение информационного объёма в тексте

Почти всегда при наборе текста на компьютерах и других электронных устройствах приходится сталкиваться с написанием различных символов. К ним следует отнести:

По всем расчётам получается, что мощность компьютерного алфавита составляет 256 различных символов и вариантов. В соответствии с формулой Хартли, N = 256, а i — масса любого из значков в клавиатурном алфавите соответствует одному байту, или восьми битам.

Размер любой напечатанной фразы может быть вычислен по формуле V=K ⋅ log2N. В этом случае N обозначает количество всех символов в алфавите, а K — это численность знаков непосредственно в напечатанной фразе. Так, например, имеется произвольный текст объёмом в 25 листов. На каждом из них расположено по 45 строчек текста, содержащих по 58 символов.

Исходя из этого, на любой отдельной странице будет 45*58 = 2610 байт информации. В целом же по всему тексту этот объём будет равен 2610*25 = 65250 байт. Для обозначения мощности алфавита в информатике общепринятым вариантом является буква N из формулы Хартли. Именно ее чаще всего указывают в большинстве учебников и профессиональной литературе.

В кодовой таблице ASCII используют восьмибитную кодировку текстовых сообщений. Она позволяет полностью вместить основной набор символов кириллического и латинского алфавитов как в строчном, так и в прописном вариантах. Также с её помощью можно отобразить знаки препинания, цифры и прочие базовые знаки. Часто пользователям приходится иметь дело с более крупными объёмами, состоящими из триллионов байтов.

Для удобства их всегда переводят в увеличенные величины — кило-, мега-, гигабайты и прочее. Для их упрощённого обозначения используются специальные сокращения: Кб, Мб, Гб и так далее. 1 Кб равняется 1024 байтам (2 байта в десятой степени), 1 Мб составляет 1024 Кб (2 Кб в десятой степени) и так далее. Исходя из этого, 65250 байт будут составлять 63,72 килобайта.

Поскольку один отдельный символ состоит из 8 битов, то устанавливать их кодировку целиком не представляется возможным. Вместо этого предпочтительнее образовать кодировку трёхбитовых комбинаций. Расчёт этого действия проводится по формуле Хартли, где n-ная степень будет равняться трём. В результате получается N, равная 8.

При определении мощности чаще всего используют алфавитный подход. Он говорит о том, что объём информации, заложенной в тексте, зависит исключительно от мощности самого алфавита и размера сообщения (то есть количества символов, содержащихся в нём). Этот показатель не имеет никакой связи со смысловым наполнением для человека.

Примеры расчёта мощности

От пользователей или обучающихся в задачах часто требуют научиться определять информационный объём какого-либо сообщения, приняв информационный вес символа за один байт. Так, в отрывке из поэмы Н. Н. Некрасова «Крестьянские дети»:

Я из лесу вышел; был сильный мороз»

будет 67 символов вместе с пробелами, то есть, в соответствии с условиями задания, 67 байт. Их количество умножают на 8 (количество битов в байте), и на выходе получается 536 битов.

Таким образом, зная в теории суть мощности, можно без проблем определять информационный объем различных сообщений.

Источник

Алфавитный подход к определению количества информации

Тип урока: Объяснение нового материала (01.10.08)

Формировать у учащихся понимание алфавитного подхода к измерению информации.

Развивать операциональное мышление и коммуникативную компетентность при обработке информации.

Воспитывать восприятие компьютера как инструмента информационной деятельности человека и бережного отношения к компьютеру.

I. Организационный момент.

II. Актуализация знаний.

III. Изложение нового материала.

V. Подведение итогов урока.

VI. Домашнее задание.

Урок проводится в компьютерном классе, доска, мел.

Основные понятия: алфавит, мощность алфавита, информационный вес символа в алфавите, производные единицы измерения информации.

I. Организационный момент

Учитель приветствует учащихся и отмечает отсутствующих.

II. Актуализация знаний

• Какое событие можно назвать информативным?

(событие информативно при условии:

1) произошло как минимум одно из двух возможных событий;

2) информация понятна, достоверна, объективна, полезна.)

• В чем заключается содержательный подход к измерению информации?

(в содержательном подходе рассматривается информативность равновероятностных событий.)

• Какую формулу используют для нахождения количества информации?

(Для нахождения количества информации используют формулу:

где N – количество всех возможных событий;

х – количество информации, содержащееся в данном сообщении.)•

Какую минимальную единицу используют для измерения количества информации?

(в качестве минимальной единицы информации используется 1 бит информации.)

Учитель предлагает детям ответить на следующие вопросы:

Сколько символов в компьютерном алфавите?

Как найти количество информации в тексте?

III. Изложение нового материала.

Вы научились определять количество информации, которое содержится в сообщениях, уменьшающих неопределенность наших, т.е. мы рассматривали информацию со своей точки зрения – с позиции человека. Для нас количество информации зависит от ее содержания, понятности и новизны. Однако любое техническое устройство не воспринимает содержание информации. Здесь не работают «неопределенность знаний» и «вероятность информации». Поэтому в вычислительной технике используется другой подход к измерению информации – алфавитный.

Алфавитный подход к измерению информации позволяет определить количество информации, заключенной тексте. Алфавитный подход является объективным, т.е. он не зависит от субъекта (человека), воспринимающего текст.

Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью (размером) алфавита. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:

Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен:

где i — информационный вес одного символа в используемом алфавите,

К— количество символов в тексте,

I – количество информации, содержащейся в тексте (информационный объем текста).

Сравнивая объемы информации русского текста и английского, мы видим, что на английском языке информации меньше, чем на русском. Но ведь содержание не изменилось! Следовательно, при алфавитном подходе к измерению информации ее количество не зависит от содержания, а зависит от мощности алфавита и количества символов в тексте. С точки зрения алфавитного подхода, в толстой книге информации больше, чем в тонкой. При этом содержание книги не учитывается.

Правило для измерения информации с точки зрения алфавитного подхода:

1) Найти мощность алфавита – N

2) Найти информационный вес одного символа i из уравнения

4) Найти количество информации – I (информационный объем всего сообщения)

Для измерения больших объемов информации используют следующие единицы:

Книга, набранная с помощью компьютера содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге?

Значит, страница содержит 40*60=2400 байт информации.

Объем всей информации в книге (в разных единицах):

2 400*150=360 000 байт; 360 000/1024=351,5625Кб; 351,5625/1024=0,34332275Мб

Ответьте на вопросы, поставленные в начале урока.

1) Сколько символов в компьютерном алфавите?

(Алфавит из 256 символов используется для представления текстов в компьютере).

2) Как найти количество информации в тексте?

(Чтобы найти количество информации в тексте надо:

1. Найти мощность алфавита – N

2. Найти информационный вес одного символа i из уравнения

4. Найти количество информации – I (информационный объем всего сообщения)

Вычислите информационный объем сообщения: Наступили холода, при условии, что один символ кодируется 1 байтом.

(Решение: K = 16, i = 1 байт, следовательно I = 16 байт = 16*8 бит = 128 бит)

3Кб в байтах и битах (3*1024байт = 3072байт*8 = 24576 бит)

5920 бит в байтах и Кб (5920 бит/8 =740 байт/1024=0,72Кб)

1. Наиболее объективным методом измерения информации является алфавитный подход

2. Информативность сообщения зависит от мощности используемого алфавита

3. При измерении информации рассматриваются объекты окружающего мира, описанные языковыми средствами.

VI. Подведение итогов урока.

Учитель выставляет оценки учащимся, выполнявшим задания у доски, комментируя их.

VII. Домашнее задание.

И.Семакин «Информатика» Базовый курс Учебник 7-9 классы § 4. Вопросы и задания стр. 24-25.

По желанию, выполнить творческое задание:

Составить кроссворд по теме «Определение количества информации».

Место работы: школьный медиокласс по расписанию его работы.

Источник

Чем больше мощность алфавита тем больше количество информации

Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.

Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.

Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.

Байт – основная единица измерения количества информации.

Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.

Производные единицы измерения количества информации

1 килобайт (Кб)=1024 байта =2 10 байтов

1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов

1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов

1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов

Методы измерения количества информации

Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:

Алфавитный подход к измерению количества информации

При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:

Вероятностный подход к измерению количества информации

Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:

I – количество информации,

N – количество возможных событий,

P_i – вероятность i-го события.

Задача 1.

Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.

Имеется 4 равновероятных события (N=4).

По формуле Хартли имеем: 4=2 i . Так как 2 2 =2 i , то i=2. Значит, это сообщение содержит 2 бита информации.

Задача 2.

Чему равен информационный объем одного символа русского языка?

В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log₂ N=log₂ 32=5 битов (2 5 =32).

Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.

Задача 3.

Чему равен информационный объем одного символа английского языка?

Задача 4.

Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.

2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.

Задача 5.

Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log₂101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log₂128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.

Задача 6.

Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.

Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p₁=1/2, p₂=1/4, p₃=1/8, p₄=1/8.

Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:

Задача 7.

Задача 8.

Оцените информационный объем следующего предложения:

Тяжело в ученье – легко в бою!

Так как каждый символ кодируется одним байтом, нам только нужно подсчитать количество символов, но при этом не забываем считать знаки препинания и пробелы. Всего получаем 30 символов. А это означает, что информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§ 1.6. Измерение информации

Информатика. 7 класса. Босова Л.Л. Оглавление

1.6.1. Алфавитный подход к измерению информации

Одно и то же сообщение может нести много информации для одного человека и не нести её совсем для другого человека. При таком подходе количество информации определить однозначно затруднительно.

Алфавитный подход позволяет измерить информационный объём сообщения, представленного на некотором языке (естественном или формальном), независимо от его содержания.

Для количественного выражения любой величины необходима, прежде всего, единица измерения. Измерение осуществляется путём сопоставления измеряемой величины с единицей измерения. Сколько раз единица измерения «укладывается» в измеряемой величине, таков и результат измерения.

При алфавитном подходе считается, что каждый символ некоторого сообщения имеет определённый информационный вес — несёт фиксированное количество информации. Все символы одного алфавита имеют один и тот же вес, зависящий от мощности алфавита. Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется 1 бит.

Обратите внимание, что название единицы измерения информации «бит» (bit) происходит от английского словосочетания binary digit — «двоичная цифра».

За минимальную единицу измерения информации принят 1 бит. Считается, что таков информационный вес символа двоичного алфавита.

1.6.2. Информационный вес символа произвольного алфавита

Разрядность двоичного кода принято считать информационным весом символа алфавита. Информационный вес символа алфавита выражается в битах.

Задача 1. Алфавит племени Пульти содержит 8 символов. Каков информационный вес символа этого алфавита?

Решение. Составим краткую запись условия задачи.

Полная запись решения в тетради может выглядеть так:

1.6.3. Информационный объём сообщения

Информационный объём сообщения (количество информации в сообщении), представленного символами естественного или формального языка, складывается из информационных весов составляющих его символов.

Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i;I = К • i.

Задача 2. Сообщение, записанное буквами 32-символьного алфавита, содержит 140 символов. Какое количество информации оно несёт?

Задача 3. Информационное сообщение объёмом 720 битов состоит из 180 символов. Какова мощность алфавита, с помощью которого записано это сообщение?

1.6.4. Единицы измерения информации

1 байт = 8 битов

Бит и байт — «мелкие» единицы измерения. На практике для измерения информационных объёмов используются более крупные единицы:

1 килобайт = 1 Кб = 1024 байта = 2 10 байтов
1 мегабайт = 1 Мб = 1024 Кб = 2 10 Кб = 2 20 байтов
1 гигабайт = 1 Гб = 1024 Мб = 2 10 Мб = 2 20 Кб = 2 30 байтов
1 терабайт = 1 Тб = 1024 Гб = 2 10 Гб = 2 20 Мб = 2 30 Кб = 2 40 байтов

Задача 4. Информационное сообщение объёмом 4 Кбайта состоит из 4096 символов. Каков информационный вес символа используемого алфавита? Сколько символов содержит алфавит, с помощью которого записано это сообщение?

Ответ: 8 битов, 256 символов.

Задача 5. В велокроссе участвуют 128 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер цепочкой из нулей и единиц минимальной длины, одинаковой для каждого спортсмена. Каков будет информационный объём сообщения, записанного устройством после того, как промежуточный финиш пройдут 80 велосипедистов?

Ответ: 70 байтов.

Самое главное.

При алфавитном подходе считается, что каждый символ некоторого сообщения имеет опредёленный информационный вес — несёт фиксированное количество информации.

1 бит — минимальная единица измерения информации.

Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i: I = K•i.

Байт, килобайт, мегабайт, гигабайт, терабайт — единицы измерения информации. Каждая следующая единица больше предыдущей в 1024 (210) раза.

Вопросы и задания.

1.Ознакомтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.

Источник