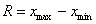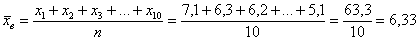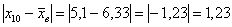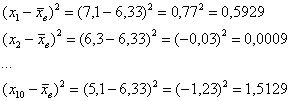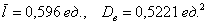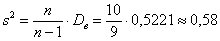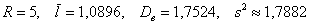Чем больше размах вариации

Вариация, размах, межквартильный размах, среднее линейное отклонение

В этой статье мы приступим к изучению показателей вариации: размах вариации, межквартильный размах, среднее линейное отклонение.

В математической статистике вариация занимает одно из центральных мест. Что же такое вариация? Это изменчивость. Вариация показателя – изменчивость показателя.

Показатели вариации дают очень важную характеристику процессам и явлениям. Они отражают устойчивость процессов и однородность явлений. Чем меньше показатель вариации, тем более процесс устойчивый, а значит, и более предсказуемый.

Показатели вариации отражают не отдельно взятые значения, а дают характеристику некоторому явлению или процессу в целом. Имея в наличии показатели среднего значения и вариации, можно получить первичное представление о характере данных. Средняя – это обобщающий уровень, а вариация характеризует, насколько среднее значение (или другой показатель) хорошо обобщает значения некоторой совокупности данных. Если показатель вариации незначительный, то значения совокупности находятся близко к среднему, следовательно, среднее значение хорошо обобщает совокупность. Если вариация большая, то среднее значение плохо обобщает данные (значения разбросаны далеко друг от друга), и получается «средняя температура по больнице».

Размах вариации

Размах вариации – разница между максимальным и минимальным значением:

Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.

С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.

Межквартильный размах

В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.

Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».

Среднее линейное отклонение

Есть показатели вариации, которые учитывают сразу все значения, а не только отдельные наблюдения (типа максимума или минимума). Одним из таких является среднее линейное отклонение. Этот показатель характеризует меру разброса значений вокруг их среднего. В чем суть? Для того, чтобы показать меру разброса данных, нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это среднее арифметическое. Далее нужно посчитать, насколько каждое значение отклоняется от средней. Нас интересует среднее из таких отклонений. Однако напрямую складывать положительные и отрицательные отклонения нельзя, т.к. они взаимоуничтожатся и их сумма будет равна нулю. Поэтому все отклонения берутся по модулю. Средне линейное отклонение рассчитывается по формуле:

a – среднее линейное отклонение,

X – анализируемый показатель,

X̅ – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

Рассчитанное по этой формуле значение показывает среднее абсолютное отклонение от средней арифметической. Наглядная картинка в помощь.

Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.

Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор провести статистический анализ длины черенков. Отобрал 10 штук и замерил их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно, в среднем на 16 см. Есть, о чем поговорить с работниками.

На этом сегодняшнюю заметку закончим. В следующей статье будут рассмотрены такие показатели вариации, как дисперсия, среднеквадратичное отклонение и коэффициент вариации.

Источник

Тема 9 Показатели вариации

Показатели вариации в анализе взаимосвязей

Для измерения степени колеблемости отдельных значений признака относительно средней исчисляют основные показатели вариации.

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так и практическое значение.

Так, например, для выявления наиболее стабильно работающего коллектива или предприятия наравне с другими показателями рассчитывают и основные показатели вариации. Эти показатели дают возможность количественно определить размеры устойчивости производительности труда, уровня квалификации, цен на основные виды выпускаемой продукции и т.п. Измерение размеров вариации такого показателя, как «выполнение работ в срок» имеет важное значение для принятия решений заказчиками и инвесторами, т.к. ситуация, в которой присутствует изменчивость признака, часто содержит риск. Осо­бое значение показатели вариации приобретают в анализе рынка ценных бумаг, где мера колеблемости отождествляется с мерой рискованности вложения денежных средств.

Основными показателями, характеризующими вариацию, являются:

1) Размах вариации

2) Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений:

где –абсолютные значения отклонений отдельных вариантов xi от средней арифметической ; fi – частота.

3. Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:

4. Среднее квадратическое отклонение – корень квадратный из дисперсии:

5. Коэффициент вариации – используется для сравнительной оценки вариации, а также для характеристики однородности совокупности:

Пример. Для иллюстрации расчетов воспользуемся данными нижеприведенной табл. 9.1:

Таблица 9.1 ‑ Данные о продаже основных марок холодильников:

Рассчитаем размах вариации.

R= 1200-460=740$

Пример вычисления размаха вариации

Размах вариации служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован для выявления ошибок. При наличии очень больших (или очень малых) ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных.

Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака.

Этого недостатка лишен другой показатель – дисперсия, рассчитываемый как средний квадрат отклонений значений признака от их средней величины.

Между индиви­дуальными отклонениями от средней и колеблемостью признака существует прямая зави­симость: чем сильнее колеблемость признака, тем больше отклонения его значений от средней величины и менее устойчив изучаемый показатель.

Как и средняя величина этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной

По приведенным выше данным определим средневзвешенную цену холодильника:

Далее рассчитаем дисперсию:

. Следует отметить, что дисперсия еще не дает представления об однородности со­вокупности, и этому показателю трудно дать экономическую интерпретацию, т.к. он рас­считан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего, на­сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность что и изучаемый признак. .

Рассчитаем среднее квадратическое отклонение

Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости ка­кого-либо одного признака или для определения однородности совокупности рассчиты­вают относительные показатели.

Эти показатели вычисляются как отношение размаха вариации, среднего линейно­го отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего эти показатели выражаются в процентах.

Определим значение показателя вариации по вышеприведенным данным таблицы

Совокупность считается однородной, если V не превышает 33%.

Если V 25% – вариация сильная.

Вывод: Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному).

!! Следует отметить, что коэффициент вариации может быть более 100%, что, в част­ности, может быть при наличии значений сильно отличающихся от средней величины. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.

Изучая вариацию интересующего нас признака в пределах исследуемой совокупно­сти и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного признака.

При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным (оказывающим влияние на взаимосвязанный с ним признак) и результативным (подвер­женным влиянию).

Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации резуль­тативного признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индиви­дуальных значений признака, используют правило сложения дисперсий.

Общая дисперсия представляет собой сумму средней из виутригрупповой и меж­групповой и дисперсий:

Общая дисперсия характеризует вариацию признака по всей совокупности как ре­зультат влияния всех факторов, определяющих индивидуальные различия единиц сово­купности.

Межгрупповая дисперсия характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результа­тивного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рас­считывается отдельно по каждой j-ой группе.

Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:

Взаимосвязь между тремя видами дисперсий получила название правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий:

Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении об­щей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчле­нения общей совокупности.

Теснота связи между факторным и результативным признаками оценивается на ос­нове эмпирического корреляционного отношения:

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

Пример. На следующем условном примере исследуем зависимость объема выполненных ра­бот от формы собственности проектно-изыскательских организаций.

Таблица 9.2. Выполнение работ проектно-изыскательскими организациями разной формы собственности

Объем выполненных работ

Форма собственности	Количество предприятий	Итого
Государственная	4	10,30,20,40	100
Негосударственная	6	20, 40, 60, 20, 50, 50	240
Итого	10	340

1) Определим средний объем работ для предприятий двух форм собственности.

2) Определим средний объем работ для каждой формы собственности.

3) Рассчитаем общую и внутригрупповые (т.е. для каждой группы) дисперсии.

4) Определим среднюю из внутригрупповых и межгрупповую дисперсию. Для этого полученные ранее данные заносятся в таблицу расчета.

Таблица 9.3. – Вспомогательная таблица

Государственная425125Негосударственная640233Итого10

Пример. Средняя из внутригрупповых дисперсий

Пример. Межгрупповая дисперсия

На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий:

Проверка закона сложения дисперсий: 54,0+189,8=243,8

Вывод: Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22% [(54,0/243,8) х 100%] зависит от фак­тора, положенного в основание группировки, т.е. от формы собственности, а на 78% [(189,8/243,8)х100%)] ‑ от прочих факторов.

Вывод о том, что объем выполненных работ в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:

Вывод: Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика

Контрольные задания

Вычислить: а) размах вариации; б)среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; относительные показатели вариации возраста студентов.

2. По данным статистических ежегодников постройте таблицу с рядом показателей и определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Оцените количественную однородность совокупности.

Источник

5. Размах вариации. Среднее линейное отклонение.
Генеральная и выборочная дисперсия

На предыдущем уроке по математической статистике мы изучили центральные показатели статистической совокупности, а именно моду, медиану, среднюю, и теперь переходим к показателям вариации. Они показывают, КАК варьируются статистические данные, а именно – насколько далеко «разбросаны» варианты относительно средних значений, да и просто друг от друга. В данной статье будут рассмотрены самые популярные показатели, и для опытных читателей сразу оглавление:

и, чтобы не «лепить» километровую простыню, разделю материал на две веб страницы:

Итак, прямо сейчас мы сформулируем определения этих показателей, узнаем соответствующие формулы и, конечно, потренируемся в конкретных вычислениях. Да не просто в конкретных, а в рациональных.

Но прежде систематизируем информацию о том, какие статистические данные могут оказаться в нашем распоряжении:

– они могут быть первичными (не обработанными), грубо говоря – это неупорядоченный список чисел, либо вторичными – это уже сформированный дискретный (Урок 2) или интервальный вариационный ряд (Урок 3).

– рассматриваемая статистическая совокупность может быть генеральной либо выборочной, и чаще, конечно, перед нами выборка.

…что-то не понятно по терминам? Срочно изучать основы предмета (Урок 1)! – это быстро и интересно, ну а я, сколько нужно, вас тут подожду 🙂

Размах вариации

Он уже встречался. Это разность между самым большим и самым малым значением статической совокупности:

при этом не имеет значения, генеральная ли нам дана совокупность или выборочная, сгруппированы ли данные или нет.

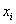
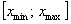
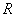
Очевидно, что все варианты исследуемой совокупности (той или иной) заключены в отрезке , а размах – есть не что иное, как его длина.

Такой вот простой, надёжный и понятный показатель. Но, несмотря на его элементарность, рассмотрим технику вычисления, и, конечно, это отличный повод размяться:

Дана статистическая совокупность
15, 17, 13, 10, 21, 17, 23, 9, 14, 19

Найти размах вариации

Решить задачу можно несколькими способами.

Способ первый, суровый – продолжаю вас готовить к борьбе с киборгами :)) Это когда под рукой нет вычислительной техники. Или когда она есть, но вы сами понимаете, как важно «прокачать» свои человеческие способности.

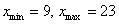
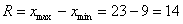
Если чисел не так много (наш случай), то максимальное и минимальное значения легко углядеть устно: и размах равен: единиц.

Если чисел больше (20-30 и даже больше), то надёжен следующий алгоритм:

1) Ищем минимальное значение. Сначала самым маленьким будет первое число: 15. Второе число (17) больше, и поэтому его пропускаем. Третье число (13) меньше, чем 15, и теперь 13 – самое малое число. И так далее, пока не закончится список.

2) Ищем максимальное значение. Сначала самым большим будет первое число: 15. Второе число (17) больше и теперь оно становится самым большим. И так далее – до конца списка.

Способ второй, более быстрый (обычно). Использование программного обеспечения, при этом числа можно просто отсортировать (по возрастанию либо убыванию) или использовать специальные функции:

Запишем ответ 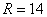ед. и с нетерпением перейдём к другим показателям, которые характеризуют степень рассеяния вариант относительно центра совокупности, прежде всего, относительно средней.

О смысле и важности этих показателей я рассказал в курсе теории вероятностей (статья о дисперсии дискретной случайной величины), но коротко повторю и сейчас. Рассмотрим двух студентов, каждый из которых в среднем учится на 3,5 балла. Но есть один нюанс. Один стабильно получает тройки-четвёрки, а другой то пятёрки, то двойки. И поэтому важно знать меру рассеяния оценок относительно средней величины. Чем она меньше – тем стабильнее учится студент.

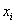
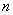
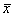
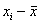
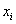
Эту меру можно оценить следующим образом: из каждой оценки (пусть их будет штук) вычитаем среднее значение . Величина называется отклонением (значения ) от средней.

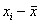
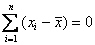
Теперь эти отклонения нужно просуммировать, но тут появляется проблема: среди разностей есть как положительные, так и отрицательные, и при их суммировании будет происходить взаимоуничтожение отклонений. Более того, итоговая сумма равна нулю: , и мы не получаем желаемого результата.

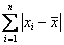
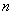
Вопрос можно решить с помощью модуля, который уничтожает минусы: , после чего осталось разделить сумму на объём совокупности и получить:

среднее линейное отклонение

– есть среднее арифметическое абсолютных отклонений всех значений статистической совокупности от средней. Это формула для несгруппированных статистических данных.

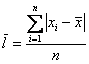
Если же в нашем распоряжении есть сформированный дискретный либо интервальный вариационный ряд, то формула будет такой:

, где – варианты (для дискретного ряда) либо середины частичных интервалов (для интервального ряда), а – соответствующие частоты.

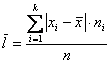
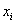
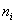
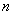
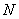
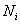
Напоминаю, что маленькая буква обычно используется для выборочной совокупности, а большая – для генеральной: – объём ген. совокупности, – частоты.

И начнём мы с малого:

В результате 10 независимых измерений некоторой величины, выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице

Требуется вычислить среднее линейное отклонение

Решение: очевидно, что перед нами первичные данные и выборочная совокупность (теоретически измерений можно провести бесконечно много). На первом шаге вычислим выборочную среднюю:

Теперь находим модули отклонений от средней: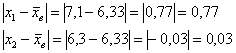

…
и так далее до:

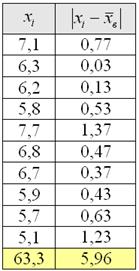
Вычисления удобно проводить на калькуляторе или в Экселе, а результаты заносить в таблицу:

На завершающем этапе рассчитываем сумму модулей:
и среднее линейное отклонение:
ед. – оно означает, что измеренные значения в среднем отличаются от примерно на 0,6 ед.

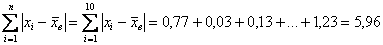
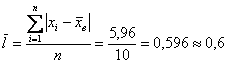
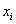
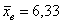
Но помимо этого, для оценки рассеяния вариант относительно средней существует более совершенный и распространённый подход. Он состоит в том, чтобы использовать не модули, а возведение отклонений в квадрат: 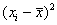(чтобы ликвидировать встречающиеся отрицательные значения).

Генеральная и выборочная дисперсия

Дисперсия с латыни так и переводится – рассеяние.

…не сломать бы язык 🙂 …так… Выборочная дисперсия – это среднее арифметическое квадратов отклонений всех вариант выборки от её средней:
– для несгруппированных данных, и:

– для сформированного вариационного ряда, где – кратные (одинаковые по значению) варианты в дискретном случае либо середины частичных интервалов – в интервальном, и – соответствующие частоты.

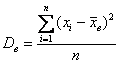
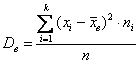
Еще раз не спеша и ОСМЫСЛЕННО прочитайте определение и выполните

Сформулировать и записать (на бумагу!) определение генеральной дисперсии и соответствующие формулы.

Свериться можно, как обычно, в конце урока.

После чего следует

продолжение Примера 13

По тем же исходным данным вычислить выборочную дисперсию

Без проблем. Вместо модулей рассчитываем квадраты отклонений:

заполняем табличку: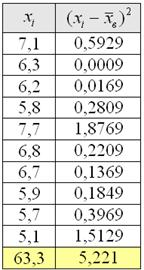

и порядок:
квадратных (!) единиц – коль скоро, мы возводили в квадрат. И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь корень. Но мы не будем торопить события, лучше посмотрим, как выполнять вычисления в Экселе:

Ответ:

Разобранная задача де-факто встречается в лабораторных работах по физике (да и не только) – когда некоторая величина замеряется раз 10 и затем рассчитывается среднее значение.

А теперь представьте, что вся ваша группа выполняет лабу по физике, и каждый провёл по 10 испытаний в схожих условиях. Очевидно, что у всех получились несколько разные выборочные значения , но все они без какой-либо закономерности (в общем случае) будут варьироваться вокруг истинного значения показателя (роль генеральной средней может играть некий теоретический эталон). Это свойство (отсутствие закономерности) называется несмещённостью оценки генеральной средней, и справедливо оно, как мы увидим ниже, не для всех показателей.

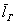
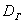
Теперь пару ласковых об отклонениях. В чём их смысл? Всё просто: у кого эти показатели ниже, тот качественнее проводит опыты (плавнее выполняет действия, точнее снимает показания с приборов, засекает время и т.п.). В идеале эти отклонения равны нулю, но это только в идеале – сам эмпиризм ситуации порождает генеральное линейное отклонение и генеральную дисперсию, которые обусловлены человеческим фактором, погрешностью приборов и так далее – вплоть до магнитных бурь.

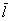
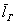
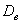
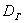
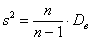
В случае с полученными линейными отклонениями – всё то же самое, они будут безо всякой закономерности варьироваться вокруг генерального значения . Но вот с дисперсией всё не так. Полученные значения выборочной дисперсии будут давать систематически заниженную оценку генеральной дисперсии . И поэтому выборочную дисперсию следует «поправить» по формуле:

– желающие могут найти обоснование этого факта и этой формулы в специализированной литературе по математической статистике.

Показатель 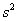так и называется – исправленная выборочная дисперсия, и вот она уже является несмещённой оценкой генеральной дисперсии.

Таким образом, каждый студент должен поправить свою дисперсию, в частности, для Примера 13:

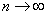
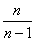
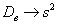
Следует отметить, что для большой выборки (от 100 и даже от 30 вариант) этой поправкой можно пренебречь, так как при дробь стремится к единице и .

И иногда дисперсию можно вовсе не поправлять. Так, в разобранном примере от нас требовалось просто вычислить выборочную дисперсию и всё. А если хочется что-то додумать, то пусть этого захочет преподаватель 🙂 Но вот если дисперсия будет «участвовать» в дальнейших действиях, то, конечно, приводим её к виду .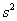

Более того, встречаются задачи, где вообще не понятно – выборочная ли дана совокупность или генеральная, и тогда разумно проявить аккуратность и использовать обозначения без подстрочных индексов, в частности, 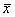и .

Теперь случай, когда дан готовый вариационный ряд. У меня опять есть подходящая советская задача про телефонную станцию, но я скорректирую условие в соответствии с современными реалиями:

В результате выборочного исследования звонков, статистик МТС получил следующие данные (за некоторый временной промежуток):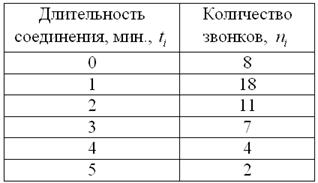

…у ОпСоСов, как известно, своя статистика – с округлением до ближайшей целой минуты :), впрочем, это тоже устареет…, как метко заметил современник, дети дружно играли во дворе – каждый в своём смартфоне(

Найти размах вариации, среднее линейное отклонение и выборочную дисперсию. Дать несмещённую оценку генеральной дисперсии и пояснить, что это означает.

Решить данную задачу в Экселе (данные и гайд уже там) либо на бумаге с помощью калькулятора.

Краткое решение и ответ совсем близко, поскольку 1-я часть урока подошла к концу, и я жду вас во 2-й части, где мы рассмотрим формулу для вычисления дисперсии, среднее квадратическое отклонение и коэффициент вариации.

Задание. Генеральная дисперсия – это среднее арифметическое квадратов отклонений всех вариант генеральной совокупности от её средней: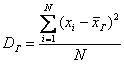
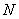
, где – объём генеральной совокупности.
Для сформированного вариационного ряда формула принимает вид: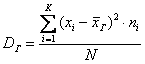
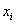
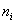
, где – либо варианты дискретного ряда, либо середины частичных интервалов интервального ряда, а – соответствующие частоты.

Пример 14. Решение: найдём размах вариации: 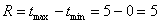мин.

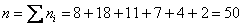
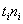
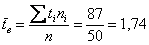
Вычислим объём совокупности , произведения , их сумму и выборочную среднюю мин.
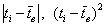
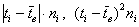
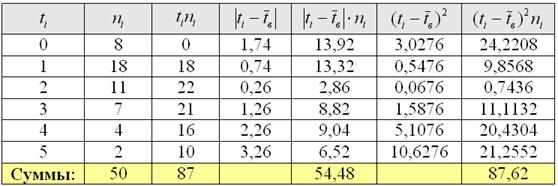
Рассчитаем , произведения и их суммы:

Среднее линейное отклонение:
мин.
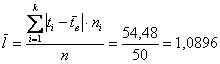
Выборочная дисперсия:
мин. в квадрате.
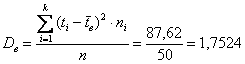
Несмещённой оценкой генеральной дисперсии является исправленная выборочная дисперсия:
мин. в квадрате.
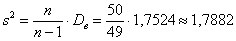
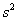
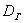
Несмещённость означает, что если в схожих условиях проводить аналогичные выборки, то полученные значения будут безо всякой закономерности варьироваться вокруг генерального значения .

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник