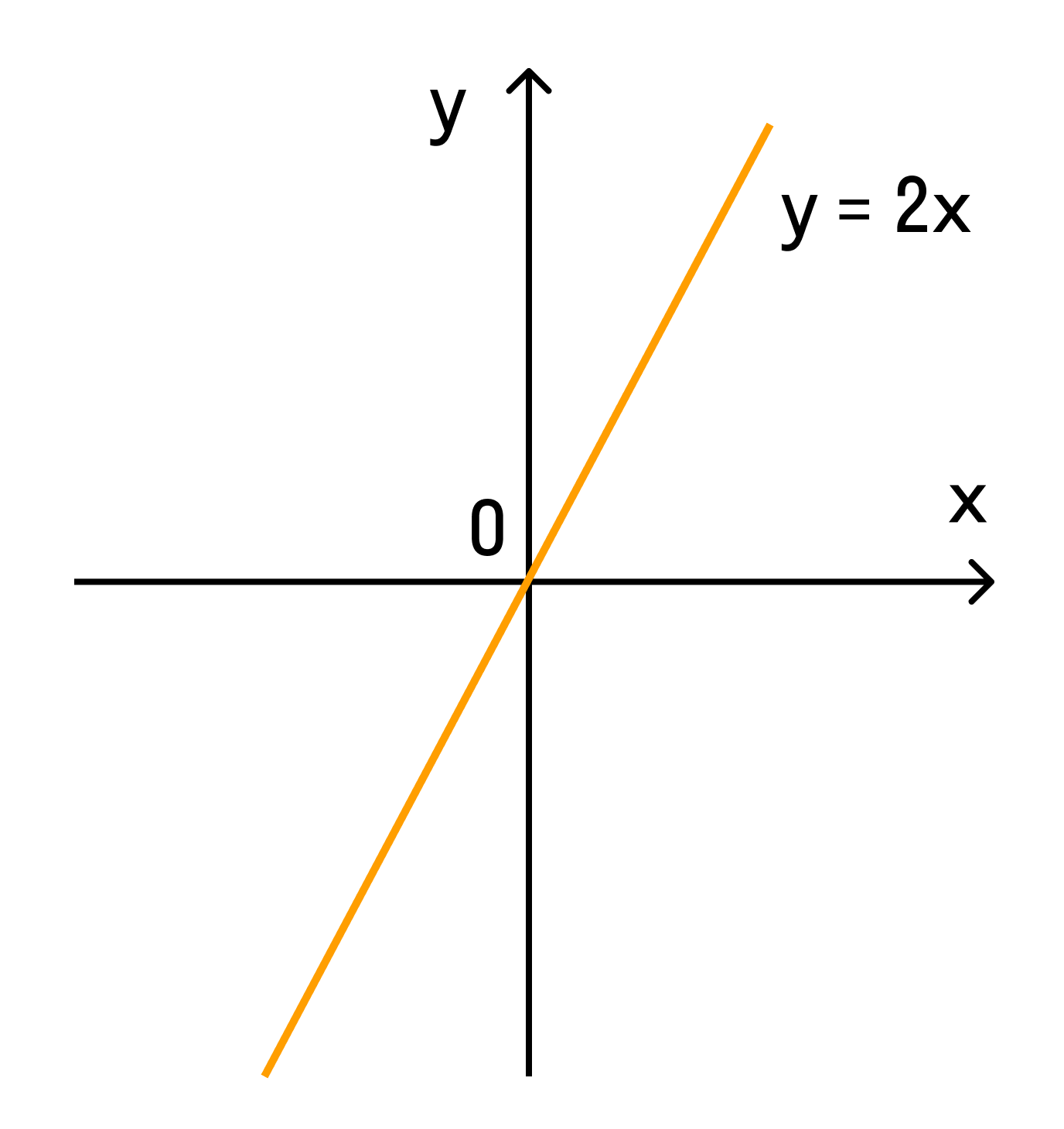Чем больше скорость тем больше время
Время, скорость, расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 м
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 м
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Тема конспекта : Скорость, время и расстояние. Применение в задачах.
Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?
Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость. А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.
Как зависит время прохождения пути от скорости?
Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.

Как найти время, зная скорость и расстояние?
Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:

Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?
Внимательно прочитайте задачу и определите, что известно из условия задачи.
Напишите на черновике эти данные.
Также напишите, что неизвестно и что нужно найти
Воспользуйтесь формулой для задач про расстояние, время и скорость
Введите в формулу известные данные и решите задачу
Решение для задачи про Зайца и Волка.
Из условия задачи определяем, что нам известно скорость и расстояние.
Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.

Пишем в черновик эти данные например так:
Расстояние до норы — 3 километра
Скорость Зайца — 1 километр за 1 минуту
Теперь запишем то же самое математическими знаками:
Вспоминаем и записываем в тетрадь формулу для нахождения времени:
Теперь запишем решение задачи цифрами:

Как найти скорость, если известно время и расстояние?
Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:
Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?
Решение задачи на движение:
В черновик записываем, что нам известно расстояние и время.
Из условия задачи определяем, что нужно найти скорость
Вспоминаем формулу для нахождения скорости.
Формулы для решения таких задач показаны на картинке ниже.

Подставляем известные данные и решаем задачу:
Расстояние до норы — 3 километра
Время, за которое Заяц добежал до норы — 3 минуты
Запишем эти известные данные математическими знаками
Записываем формулу для нахождения скорости
Теперь запишем решение задачи цифрами:

Как найти расстояние, если известно время и скорость?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:
Заяц убегал от Волка со скоростью 1 километр за 1 минуту. Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?
Решение задачи: Записываем в черновик, что нам известно из условия задачи:
Скорость Зайца — 1 километр за 1 минуту
Время, которое Заяц бежал до норы — 3 минуты
Теперь, то же самое запишем математическими знаками:
Вспоминаем формулу для нахождения расстояния:
Прямая и обратная пропорциональность
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Зависимости также можно классифицировать по формам: функциональная и статистическая.
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.
В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.
Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.
Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
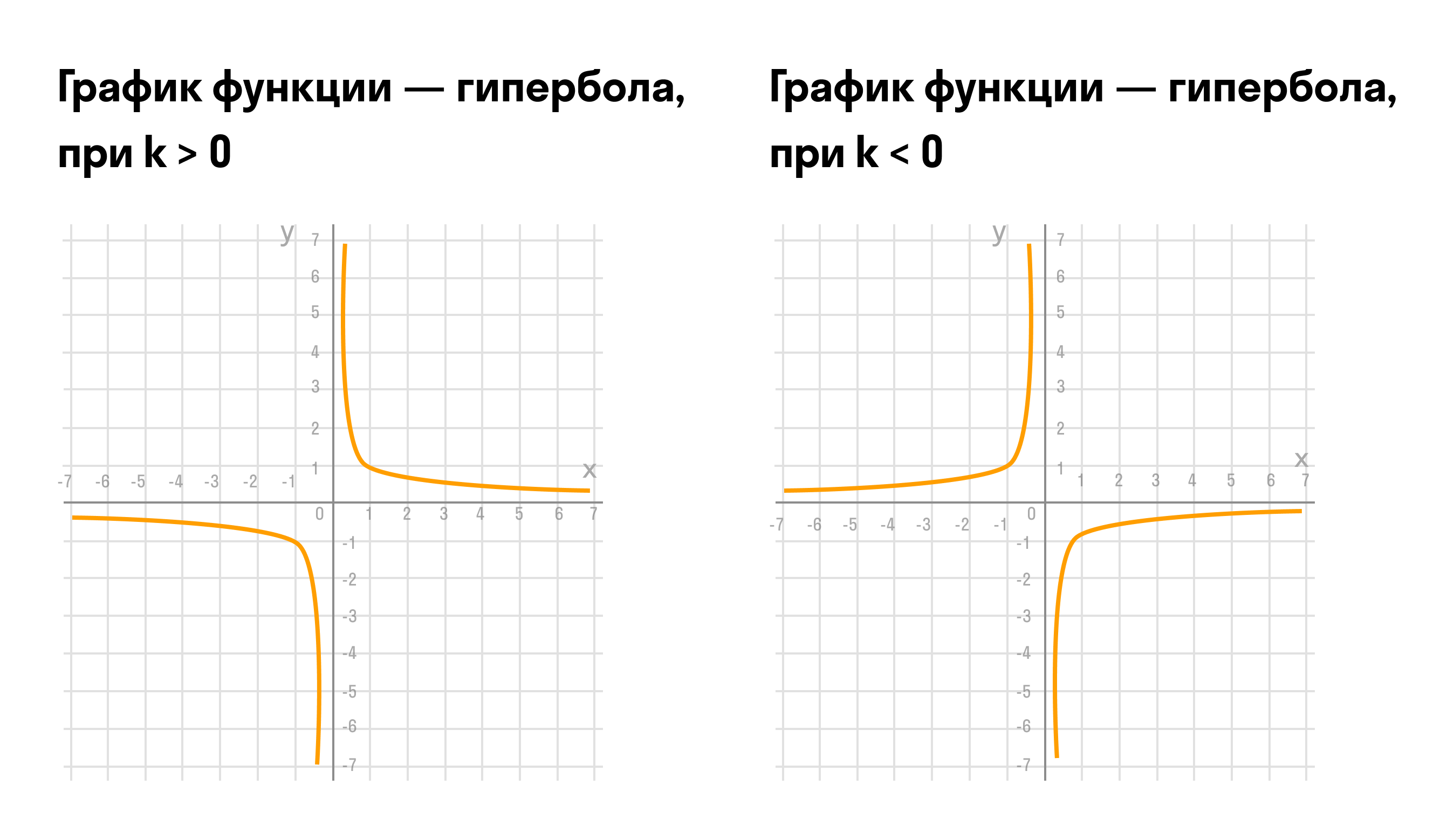
Графиком обратно пропорциональной зависимости величин является гипербола.
Свойства функции обратной пропорциональности:
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.
Время эластично: почему на вершине горы время идет быстрее, чем на пляже?
Гравитация, как мы знаем сегодня, обладает способностью искривлять пространство и время. Как утверждал Эйнштейн в Общей теории относительности (ОТО), время, по мере приближения к Земле, идет медленнее. Это происходит из-за того, что гравитация большой массы, например, такой как наша планета, искривляет пространство и время вокруг нее. Этот эффект называется «эффектом замедления времени» и он проявляется даже на малых уровнях. Однако за пределами физических законов мы воспринимаем время иначе, точнее, искаженно. Так, если поместить одни часы на вершине горы, а другие оставить на пляже, то в конце-концов вы увидите, что все часы показывают разное время. Ученые впервые наблюдали эффект замедления времени в космическом масштабе, когда звезда проходила рядом с черной дырой. Затем тот же эффект был зафиксирован в меньших масштабах – исследователи использовали пару чрезвычайно точных атомных часовых механизмов, причем одни часы были расположены на 33 сантиметра выше, чем другие. Результаты показали, что время снова замедлилось на часах, расположенных ближе к Земле.
Время неоднородно: оно течет с разной скоростью в зависимости от того, где вы находитесь и с какой скоростью двигаетесь.
Атомные часы – прибор для измерения времени. В качестве периодического процесса используются собственные колебания, связанные с процессами, происходящими на уровне атомов или молекул.
Эффект замедления времени
Замедление времени восходит к Специальной теории относительности (СТО) Эйнштейна, согласно которой движение в пространстве на самом деле создает изменения в течении времени. Чем быстрее вы движетесь через три измерения, которые определяют физическое пространство, тем медленнее вы движетесь через четвертое измерение – время, по крайней мере, относительно другого объекта. Так, часы в движении будут тикать медленнее, чем часы на земле. Если двигаться со скоростью, близкой к скорости света, эффект будет гораздо более выраженным.
Важно понимать, что замедление времени – это не мысленный эксперимент или гипотетическая концепция, а реальность. Это доказали эксперименты Хафеле-Китинга, проведенные в 1971 году, когда на самолетах, летящих в противоположных направлениях, были установлены два атомных часовых механизма. Относительное движение на самом деле оказало измеримое воздействие и создало разницу во времени между двумя часами. Это также было подтверждено в других физических экспериментах.
Почему мы помним прошлое, а не будущее?
Но есть еще одна примечательная деталь: замедление времени в результате гравитационных эффектов. Возможно, вы видели фильм Кристофера Нолана «Интерстеллар», где близость черной дыры заставляет время на другой планете чрезвычайно замедляться (один час на этой планете равен семи земным годам). Эта форма замедления времени также реальна. Все дело в Общей теории относительности Эйнштейна, о чем написано в начале статьи – гравитация может искривлять пространство-время, а следовательно, и само время. А значит, абсолютного времени не существует.
Чем ближе часы к источнику гравитации, тем медленнее проходит время; чем дальше часы от источника гравитации, тем быстрее будет идти время.
Выходит, для всех часов в мире и для каждого из нас время течет немного по-разному. Но даже если время течет с постоянно меняющимися скоростями по всей Вселенной, время все равно течет в каком-то объективном смысле, верно? Или нет?
Физика без времени
В своей книге «Порядок времени» итальянский физик-теоретик Карло Ровелли предположил, что наше восприятие времени — наше ощущение, что время вечно течет вперед – может быть в высшей степени субъективной проекцией. В конце-концов, когда вы смотрите на реальность в наименьшем масштабе (используя уравнения квантовой гравитации, например), время исчезает.
Итак, почему мы воспринимаем время как движение вперед? Ровелли отмечает, что, хотя время исчезает в чрезвычайно малых масштабах, мы наблюдаем энтропию: порядок превращается в беспорядок; яйцо разбивается и становится яичницей. Ровелли пишет, что ключевые аспекты времени описаны во втором законе термодинамики, который гласит, что тепло всегда переходит от горячего к холодному, как улица с односторонним движением. Например, кубик льда тает в чашке горячего чая, а не наоборот. Ровелли предполагает, что подобный феномен может объяснить, почему мы способны воспринимать только прошлое, а не будущее.
«Каждый раз, когда будущее определенно отличается от прошлого, возникает что-то вроде тепла», — писал Ровелли в статье для Financial Times.
Термодинамика прослеживает направление времени к чему-то, называемому «низкой энтропией прошлого», все еще загадочному явлению, о котором бушуют дискуссии.» «Рост энтропии ориентирует время и допускает существование следов прошлого, а они допускают возможность воспоминаний, которые скрепляют наше чувство идентичности. Я подозреваю, что то, что мы называем «течением» времени, следует понимать, изучая структуру нашего мозга, а не изучая физику: эволюция превратила наш мозг в машину, которая питается памятью, чтобы предвидеть будущее. Вот к чему мы прислушиваемся, когда прислушиваемся к течению времени. Таким образом, понимание «течения» времени может иметь большее отношение к нейробиологии, чем к фундаментальной физике. Поиск объяснения ощущения потока в физике может оказаться ошибкой.
Ученым еще многое предстоит узнать о том, как мы воспринимаем время и почему оно действует по-разному в зависимости от масштаба. Но несомненно то, что за пределами физики наше индивидуальное восприятие времени также удивительно эластично.
Еще больше увлекательных статей о последних научных открытиях в области физики, читайте на нашем канале в Яндекс.Дзен. Там регулярно выходят статьи, которых нет на сайте.
Странная субъективность времени
На вершине горы время движется иначе, чем на пляже. Но чтобы испытать искажение восприятия времени, не нужно отправляться в горы или на море. Так, в моменты сильного страха мозг выделяет большое количество адреналина, который ускоряет внутренние часы, заставляя воспринимать внешний мир как движущийся очень медленно.
Ровелли отмечает, для работы в области квантовой гравитации придется столкнуться с вопросами о природе времени.
Еще одно распространенное искажение возникает, когда мы фокусируем свое внимание определенным образом. Как отмечает Аарон Сакетт, адъюнкт-профессор маркетинга в Университете Сент-Томаса в интервью Gizmodo, если вы думаете о том, как в настоящее время проходит время, самым главным фактором, влияющим на ваше восприятие времени, является внимание.
Чем больше внимания вы уделяете течению времени, тем медленнее оно течет.
Когда вы отвлекаетесь от течения времени – возможно, от чего—то интересного, происходящего поблизости, вы с большей вероятностью теряете счет времени. Создается стойкое ощущение, что оно ускользает быстрее, чем раньше. Известная поговорка гласит: «Время летит, когда тебе весело», но реальность больше похожа на «время летит, когда ты думаешь о других вещах».
В свою очередь Ровелли считает, что то, что мы называем временем – это богатая, стратифицированная концепция, имеющая множество слоев. Некоторые слои времени применимы только в ограниченных масштабах в ограниченных областях, но это не делает их иллюзиями.Иллюзией является представление о том, что время течет с абсолютной скоростью. Река времени может течь вечно вперед, но она движется с разной скоростью, между людьми и даже внутри вашего собственного разума.