Чем больше выборка тем больше
Выборка. Типы выборок
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени. Примеры генеральных совокупностей
Оглавление
Генеральная совокупность
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени. Примеры генеральных совокупностей
Выборка (Выборочная совокупность)
Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности.
Репрезентативность выборки
Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей.
В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках соответственно.
Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от ошибки никак не зависит от размера выборки.
Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой всех москвичей.
Влияние размера статистической выборки на качество научного исследования
Любая научная работа (особенно в психологии, медицине) предполагает проведение некоего эксперимента для сбора доказательств и оценки реальной ситуации. Притом чем больше факторов учитывает автор, тем точнее результаты исследования и возможности их использования в дальнейшем.
Любая научная работа (особенно в психологии, медицине) предполагает проведение некоего эксперимента для сбора доказательств и оценки реальной ситуации. Притом чем больше факторов учитывает автор, тем точнее результаты исследования и возможности их использования в дальнейшем.
В любом эксперименте важно определить оптимальный объем выборки, который бы позволили получить достоверный результат. В этой статье Вы узнаете, какое число испытуемых считается достаточным, и как грамотно подобрать объем выборки для собственного исследования.
Влияет ли объем выборки на результаты исследования?
Результаты исследования зависят от множества факторов: объем и достоверность первоначальных данных, цель (достижимая и реалистичная или не поддающаяся измерению и достижению), качество материалов (достоверные, актуальные и пр.) и т.д. Если научное изыскание предполагает проведение практических мероприятий, то одним из важнейших моментов являются определение объема выборки.

Объем выборки представляет собой число испытуемых, которое будет принимать участие в эксперименте и подлежать оценке. Количество респондентов, их действия напрямую отражаются на результатах исследования. Если в эксперименте будет участвовать малая часть испытуемых, то не всегда будет возможно получить репрезентативные результаты.
Большое число участников же в значительной степени усложняет ход исследования, но позволяет получить более точные результаты при условии, если исследователь внимательно следит за ходом событий и учитывает все факторы, погрешности и отклонения и пр.
Таким образом, объем выборки влияет не только на точность измерений, но и качество исследования.
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
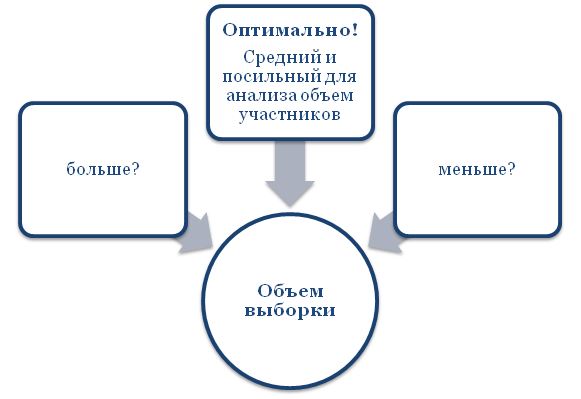
Больше – лучше, или наоборот?
Казалось бы, чем больше число испытуемых, тем точнее результаты. На самом деле, здесь палка о двух концах.
С одной стороны, большое число испытуемых позволяет получить более точные результаты исследования, определить динамику или тенденции развития событий. В то же время внушительное количество респондентов требует более пристального внимания со стороны автора: моментальное фиксирование результатов, контроль за каждым индивидом, оценка всех действий и достижений/итогов и пр. Сможет ли автор в одиночку уследить за 100-200 и более испытуемыми.
Во-вторых, большой объем выборки провоцирует рождение более высоких затрат на организацию и проведение эксперимента: привлечение сторонних экспертов для контроля за ходом исследования, подготовка дополнительных материалов для испытуемых (анкеты или опросники, задания, создание специальных условий (например, для проживания и пр.)) и т.д.
Небольшой объем выборки – самый оптимальный в плане затратности, но он дает менее точные результаты. Если в эксперименте принимает участие всего 2-4 человека, то это не значит, что выборка будет репрезентативной. В данной ситуации автор оценит лишь частный случай, но не данные генеральной совокупности.
Поэтому чтобы результаты исследования были пригодными для более широкой аудитории, важно, чтобы выборка оказалась репрезентативной, а для этого необходимо подобрать оптимальное число испытуемых.
Какой объем выборки считается оптимальным?
Объем выборки зависит не только от вида исследования, но и его масштабов. Например, в социологических опросах принято проводить соответствующие мероприятия (например, задать вопросы всем подряд или конкретной группе) с целью определения общественного мнения. Как правило, в таких проектах принимает участие свыше 1000 человек.

В психологических и медицинских экспериментах и исследованиях количество испытуемых гораздо меньше, так как обработка данных здесь может занять более длительное время, а информация обладает таким свойством как актуальность, которая может быть утрачена из-за медлительности. Оптимальным числом для таких научных изысканий считается 10-30 человек, притом все испытуемые подлежат строгой классификации по конкретному признаку.
Оптимальный объем выборки – это то количество изучаемых объектов и явлений, которое позволяет получить достоверный и максимально точный (приближенный) результат с минимальными погрешностями, который можно «репрезентовать» на более широкий круг лиц. В случае нерепрезентативности выборки исследователь получит «частный эксперимент» с субъективной оценкой происходящего.
Как определить оптимальный объем выборки для научного исследования?
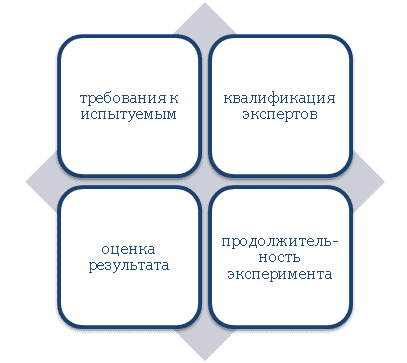
Каждый исследователь самостоятельно определяет, какой объем выборки для него оптимальный. Данный параметр зависит от ряда условий:
Оптимальный объем выборки предполагает подбор стольких испытуемых, за которыми посильно проследить и оценить их результаты без лишних затрат времени, материальных и иных ресурсов с учетом располагаемых сил.
Если исследование предполагает оценку конкретной ситуации в определенной отрасли, то достаточно подобрать 10-30 участников, соответствующих конкретных условиям и требованиям.
Если же научное изыскание носит глобальный масштаб, то необходимо подобрать опытную и сильную команду, грамотно распределить обязанности, а затем, исходя из общих возможностей команды, определить объем выборки: до 100 участников, от 101 до 500, более 500 и пр.
В идеале на каждого «контролера» должно приходиться не более 10-20 испытуемых, чтобы качество получаемых данных было высоким, а жизнь контролера проходила не только в стенах «лаборатории». Поэтому объему выборки необходимо уделять особое внимание, так как именно этот критерий позволяет получить более качественные результаты научных и иных изысканий.
Трудности с учебой?
Помощь в написании студенческих и
аспирантских работ!
Как определить размер выборки?
Статистика знает все. И Ильф и Е. Петров, «12 Стульев»
Представьте себе, что вы строите крупный торговый центр и желаете оценить автомобильный поток въезда на территорию парковки. Нет, давайте другой пример… они все равно этого никогда не будут делать. Вам необходимо оценить вкусовые предпочтения посетителей вашего портала, для чего необходимо провести среди них опрос. Как увязать количество данных и возможную погрешность? Ничего сложного — чем больше ваша выборка, тем меньше погрешность. Однако и здесь есть нюансы.
Теоретический минимум
Не будет лишним освежить память, эти термины нам пригодятся далее.
Уже в самих определениях ошибки первого и второго рода имеется простор для дебатов и толкований. Как с ними определиться и какую выбрать в качестве нулевой? Если вы исследуете уровень загрязнения почвы или вод, то как сформулируете нулевую гипотезу: загрязнение присутствует, или нет загрязнения? А ведь от этого зависит объем выборки из общей популяции объектов.
Исходная популяция, также как и выборка может иметь любое распределение, однако среднее значение имеет нормальное или гауссово распределение благодаря Центральной Предельной Теореме.
Относительно параметров распределения и среднего значения в частности возможно несколько типов умозаключений. Первое из них называется доверительным интервалом. Он указывает на интервал возможных значений параметра, с указанным коэффициентом доверия. Так например 100(1-α)% доверительный интервал для μ будет таким (Ур. 1).
Второе из умозаключений — проверка гипотезы. Оно может быть примерно таким.
Если нам нужно проверить значение μ для одной выборки из общей совокупности, то критерий обретет вид.
Как видим погрешность действительно уменьшается вместе с ростом количества входных данных. Откуда легко вывести искомое (Ур. 4).
Практика — считаем с R
Проверим гипотезу о том, что среднее значение данной выборки количества насекомых в ловушке равно 1.
и наконец получаем критический интервал для среднего значения: 1.05 — 2.22.
В итоге, следует отбраковать H0 и принять H1 так как с вероятностью 95%, μ > 1.
Поправка на ветер
На самом деле нет никаких причин, полагать, что нам будет известна σ (дисперсия), в то время как μ (среднее) нам еще только предстоит оценить. Из-за этого уравнение 4 имеет мало практической пользы, кроме особо рафинированных примеров из области комбинаторики, а реалистичное уравнение для n несколько сложнее при неизвестной σ (Ур. 5).
Обратите внимание, что σ в последнем уравнении не с шапкой (^), а тильдой (
). Это следствие того, что в самом начале у нас нет даже оценочного стандартного отклонения случайной выборки — , и вместо нее мы используем запланированное —
. Откуда же мы берем последнее? Можно сказать, что с потолка: экспертная оценка, грубые прикидки, прошлый опыт и т. д.
А что на счет второго слагаемого правой стороны 5-го уравнения, откуда оно взялось? Так как , необходима поправка Гюнтера.
Помимо уравнений 4 и 5 есть еще несколько приблизительно-оценочных формул, но это уже заслуживает отдельного поста.
Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).
Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
| ШПАРГАЛКА (скопируйте ссылку или текст) Подходы к решению проблемы: Случай 1. Генеральная совокупность значительно больше выборки: Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B ) где Например, Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/ 1000 ) = 0,031 = ±3,1 % При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически. 2. Причины «раздувать» выборку Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах). Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке. Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4). При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1). Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел. Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение: Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки. При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться). КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:Объём генеральной совокупности (N): Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам. Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
1) если объем выборки значительно меньше генеральной совокупности:
2) если объем выборки сопоставим с объемом генеральной совокупности: В приведенных формулах: Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96. N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1). p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2. Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%. n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ: Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит: n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек. Объём генеральной совокупности (N): Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки). Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму. Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются. Ошибка выборки для доли признака рассчитывается по следующим формулам. 1) если объем выборки значительно меньше генеральной совокупности: (в данной формуле не используется показатель объема генеральной совокупности N) 2) если объем выборки сопоставим с объемом генеральной совокупности: В приведенных формулах: Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96. N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1). n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы. p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2. Δ– предельная ошибка выборки. ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА: Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%): ∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48% Рассчитаем доверительный интервал: Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%). Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким. Объём генеральной совокупности (N): Среднее значение (x̄): Стандартное отклонение (s): Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки). Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму. Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются. Ошибка выборки для среднего значения рассчитывается по следующим формулам. 1) если объем выборки значительно меньше генеральной совокупности: (в данной формуле не используется показатель объема генеральной совокупности N) 2) если объем выборки сопоставим с объемом генеральной совокупности: В приведенных формулах: Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96 N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1). n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки Δ – предельная ошибка выборки. ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ: Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%): ∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44 Рассчитаем доверительный интервал: Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий. Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы. Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах. В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия: В калькуляторе используются следующие вводные данные: Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2. Объем выборки (n) – это количество людей, которые опрашиваются в исследовании. Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются? Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы. Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах. В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия: В калькуляторе используются следующие вводные данные: Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Среднее значение ( ̅x) – среднее арифметическое показателя. Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле: Объем выборки (n) – это количество людей, которые опрашиваются в исследовании. Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
|















