Чем больше жесткость пружины тем
Жесткость пружины
Максимальная сила сжатия или растяжения пружины не зависит от количества рабочих витков! Это означает, что если взять, например, цилиндрическую пружину сжатия, а затем разрезать её на две неравные по высоте части, то максимальное усилие при полном сжатии.
. обеих образовавшихся пружин будет одинаковым. Более того – максимальная сила останется такой же, как у исходной пружины!
В чем же тогда различие между тремя рассмотренными выше пружинами? Ответ на этот вопрос – в высотных размерах и жесткостях.
Меньшая пружина самая жесткая. У нее самый малый ход от свободного состояния до полного сжатия. Исходная пружина (до разделения) – самая мягкая. У нее самый большой ход.
Жесткость пружины ( C ) является ключевым параметром, определяющим силу сжатия или растяжения ( Fi ) при определенной величине деформации ( L0— Li ):
Fi = C *( L0 — Li )
В свою очередь сама жесткость пружины ( C ) зависит только от жесткости одного витка ( C1 ) и числа рабочих витков ( N ):
C = C1 / N
Обратите внимание – жесткость одного витка всегда больше жесткости всей пружины! Причем, чем больше в пружине витков, тем она мягче.
Расчет в Excel жесткости витка пружины.
Жесткость витка пружины – это «краеугольный камень в фундаменте» расчетов, зависящий лишь от модуля сдвига материала, из которого пружина навита и её геометрических размеров.
C1 = G * X 4 /( Y *( D1 — B ) 3 )
G – модуль сдвига материала проволоки
Для пружинной стали:
G ≈78500 МПа ±10%
Для пружинной бронзы:
G ≈45000 МПа ±10%
X – минимальный размер сечения проволоки
Для круглой проволоки – это её диаметр:
X = D
Для прямоугольной проволоки:
X = H при H B
X = B при B H
H – высота сечения проволоки в направлении параллельном оси навивки пружины
B – ширина сечения проволоки в направлении перпендикулярном оси навивки пружины
Для круглой проволоки:
H = B = D
D1 — наружный диаметр пружины
( D1 — B ) – средний диаметр пружины
Y – параметр жесткости сечения проволоки
Для круглой проволоки:
Y =8
Для прямоугольной проволоки:
Y =f( H / B )
Выполним аппроксимацию в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
Как видно из таблицы и графиков полученные уравнения весьма точно замещают табличные данные! Величина достоверности аппроксимации R 2 очень близка к 1 и относительная погрешность не превышает 2,7%!
Применим на практике полученные результаты.
Расчет пружины сжатия из проволоки прямоугольного сечения.
Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.
Представленная ниже программа является переработанной версией программы расчета цилиндрических пружин из круглой проволоки, подробное описание которой вы найдете, перейдя по ссылке. Прочтите эту статью, и вам проще будет разобраться в алгоритме.
Основным отличием в расчете, как вы уже догадались, является определение жесткости витка ( C1 ), задающей жесткость пружины ( C ) в целом.
Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.
Внимание.
После выполнения расчета по программе выполняйте проверку касательных напряжений.
При 1 H / B Y =5,4962*( H / B ) (-1.715)
При 2 H / B Y =3,9286*( H / B ) (-1. 2339 )
6. При H B : C1 =(78500* H 4 )/( Y *( D1 — B ) 3 )
При H > B : C1 =(78500* B 4 )/( Y *( D1 — B ) 3 )
8. Tnom =1,25*( F2 / C1 )+ H
9. Tmax =π*( D1 — B )*tg (10°)
11. S3 = T — H
12. F3 = C1 * S3
14. N расч =( L2 — H )/( H + F3 / C1 — F2 / C1 )
16. C = C1 / N
17. L0 = N * T + H
18. L3 = N * H + H
19. F2 = C * L0 — C * L2
21. F1 = C * L0 — C * L1
22. N1 = N +1,5
23. A =arctg ( T /(π*( D1 — H )))
24. L разв =π* N1 *( D1 — H )/cos ( A )
25. Q = H * B * Lразв *7,85/10 6
Заключение.
Значение модуля сдвига ( G ) материала проволоки в существенной мере влияющее на жесткость пружины ( C ) в реальности колеблется от номинально принятого до ±10%. Это обстоятельство и определяет в первую очередь наряду с геометрической точностью изготовления пружины «правильность» расчетов усилий и соответствующих им перемещений.
Почему в расчетах не используются механические характеристики (допускаемые напряжения) материала проволоки кроме модуля упругости? Дело в том, что, задаваясь углом подъема витка и индексом пружины в ограниченных диапазонах значений, и придерживаясь правила: «угол подъема в градусах близок значению индекса пружины», мы фактически исключаем возможность возникновения касательных напряжений при эксплуатации превышающих критические величины. Поэтому проверочный расчет пружин на прочность имеет смысл производить лишь при разработке пружин для серийного производства в особо ответственных узлах. Но при таких условиях кроме расчетов всегда неизбежны серьезные испытания…
Напишите пару строк в комментариях — мне всегда интересно ваше мнение.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
ОСТАЛЬНЫМ можно скачать просто так. — никаких паролей нет!
Сила упругости
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Сила упругости: Закон Гука
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Какой буквой обозначается сила упругости?
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
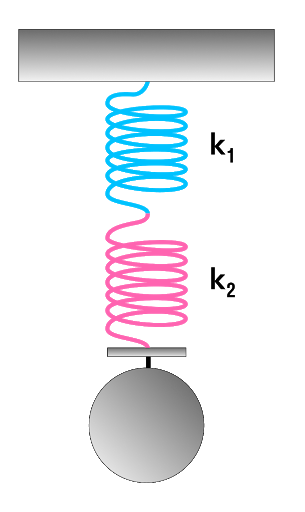
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
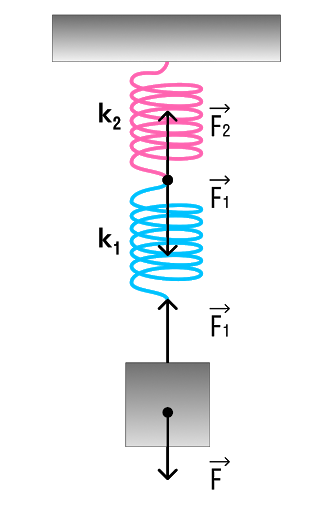
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
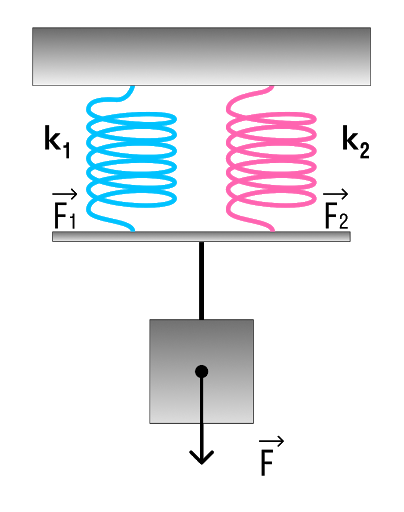
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
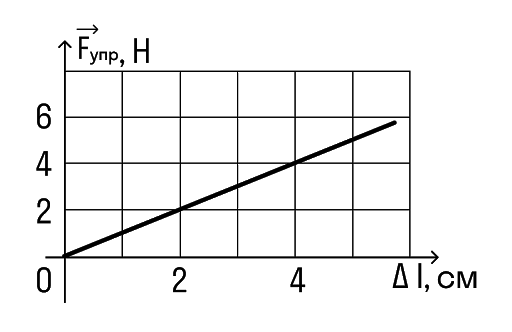
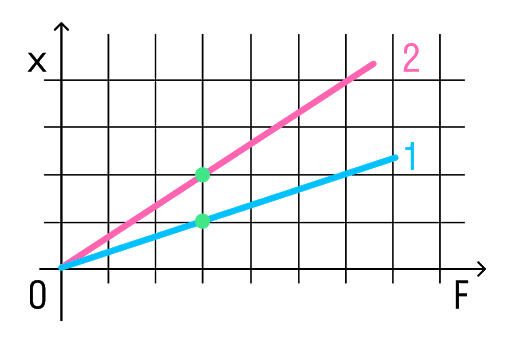
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
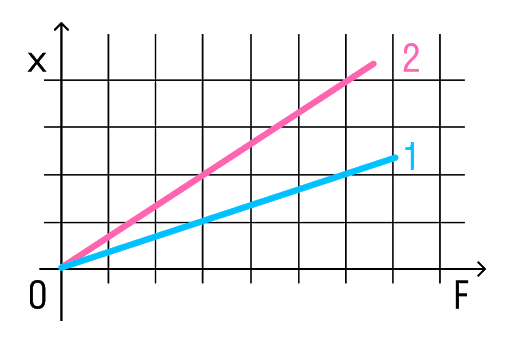
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Сила упругости
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина \(L_<0>\) пружины.
Подвесим теперь к пружине груз. Пружина будет иметь длину \(L\), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
\[ \large L_ <0>+ \Delta L = L \]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину \(L_<0>\).
\( L_ <0>\left(\text <м>\right) \) – начальная длина пружины;
\( L \left(\text <м>\right) \) – конечная длина растянутой пружины;
\( \Delta L \left(\text <м>\right) \) – кусочек длины, на который растянули пружину;
Величину \( \Delta L \) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
\( \varepsilon \) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал \( F_<\text<упр>> \) силой упругости.
\[ \large \boxed< F_<\text<упр>> = k \cdot \Delta L >\]
Эту формулу назвали законом упругости Гука.
\( F_<\text<упр>> \left( H \right) \) – сила упругости;
\( \Delta L \left(\text <м>\right) \) – удлинение пружины;
\( \displaystyle k \left(\frac
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
\[ \large F_<\text<упр>> — m \cdot g = 0 \]
Подставим в это уравнение выражение для силы упругости
\[ \large k \cdot \Delta L — m \cdot g = 0 \]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины \(\Delta L \) пружины. Получим выражение для коэффициента жесткости:
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину \(\Delta L\). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом \(mg\).
\[ \large k_ <1>\cdot \Delta L = m \cdot g \]
Две параллельные пружины:
\[ \large k_<\text<параллел>> \cdot \Delta L \cdot \frac<1><2>= m \cdot g \]
Так как правые части уравнений совпадают, левые части тоже будут равны:
\[ \large k_<\text<параллел>> \cdot \Delta L \cdot \frac<1><2>= k_ <1>\cdot \Delta L \]
Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:
Умножим обе части полученного уравнения на число 2:
Коэффициент жесткости \(k_<\text<параллел>>\) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину \(\Delta L\). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину \(\Delta L\).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом \(mg\).
\[ \large k_ <1>\cdot \Delta L = m \cdot g \]
Две последовательные пружины:
\[ \large k_<\text<послед>> \cdot \Delta L \cdot 2 = m \cdot g \]
Так как правые части уравнений совпадают, левые части тоже будут равны:
\[ \large k_<\text<послед>> \cdot \Delta L \cdot 2 = k_ <1>\cdot \Delta L \]
Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:
Разделим обе части полученного уравнения на число 2:
Коэффициент жесткости \(k_<\text<послед>>\) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину \(\Delta L \) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
\[ \large \boxed < E_
= \frac
\( E_
\left( \text <Дж>\right)\) – потенциальная энергия сжатой или растянутой пружины;
\( \Delta L \left(\text <м>\right) \) – удлинение пружины;
\( \displaystyle k \left(\frac