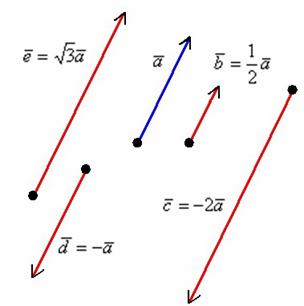
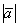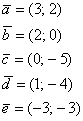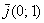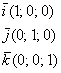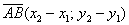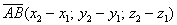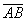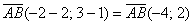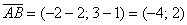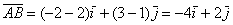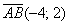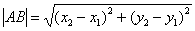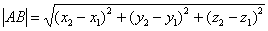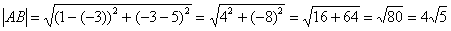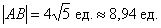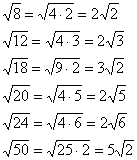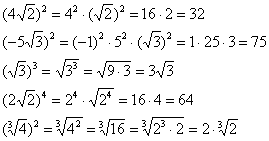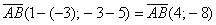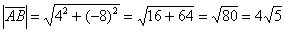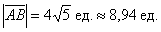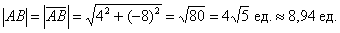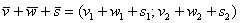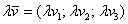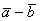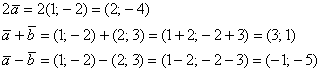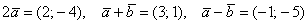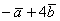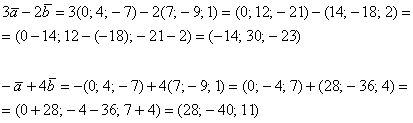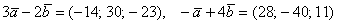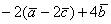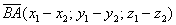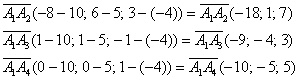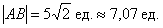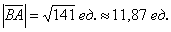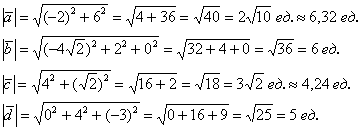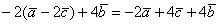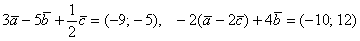Чем для вектора ав является длина отрезка ав
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
Нулевой вектор
Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Равными называются сонаправленные вектора, у которых длины равны.
Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Углы между векторами
Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).
Геометрия
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Понятие вектора
Рассмотрим простейшую задачу. Корабль, двигатель которого развивает скорость 20 км/ч, плывет по течению реки, при этом скорость течения составляет 2 км/ч. Какова скорость корабля относительно берега? Очевидно, в данном случае надо сложить скорость течения и собственную скорость корабля:
20 км/ч + 2 км/ч = 22 км/ч
Теперь посмотрим на почти такую же задачу, которая отличается лишь тем, что корабль плывет уже против течения. Для ее решения скорости уже придется вычитать:
Получается, что ответ задачи во многом зависит не только от величин скоростей, но и от их направления. Возможны и более сложные случаи, когда корабль двигается на воде перпендикулярно течению или, например, под углом в 60°. Величины, при операции с которыми необходимо учитывать их направление, называют векторными величинами, или просто векторами.
Помимо скорости к ним относят ускорение, силу, импульс, напряженность магнитного и электрического поля и многие другие величины. Те же величины, для которых нельзя указать направление, называют скалярными величинами. Это масса, температура, плотность и т. п. Для выполнения действий с векторами необходимо разработать общие правила их сложения, вычитания, умножения, которые будут справедливы независимо от физической природы векторных величин. И разработать эти правила помогает как раз геометрия.
Для начала введем понятие вектора. Любой отрезок имеет два конца, которые обычно не отличают друг от друга. Однако если одну из этих точек считать началом отрезка, а другую – собственно концом, то у отрезка появится направление. В таком случае его можно считать вектором.
Часто вектора называют направленными отрезками. Обозначают их с помощью стрелок.
На этом рисунке показан вектор, начало которого находится в точке А, а конец – в точке В. При записи в формулах сначала пишут букву, означающую начало вектора, потом обозначение его конца, а над этими двумя буквами ставят стрелочку:
С практической точки зрения приходится вводить в рассмотрение особый нулевой вектор. У него начало и конец совпадают, то есть он представляет собой всего лишь одну точку:
Нулевой вектор необходим, так как нам необходимо научиться выполнять действия над векторами. Мы знаем, что в обычной алгебре используется число ноль. В векторной же алгебре аналогом нуля является как раз нулевой вектор.
Каждый вектор имеет свою длину, которая равна расстоянию между его началом и концом. То есть, если его начало находится в точке А, а конец в точке В, то длина вектора будет совпадать с длиной отрезка АВ. Обозначают длину с помощью вертикальных скобок:
Естественно, что длина нулевого вектора равна нулю.
Задание. Найдите модуль вектора, изображенного на рисунке:
Решение. Легко выполнить построение, при котором вектор окажется гипотенузой в прямоугольном треугольнике
Тогда длину вектора можно найти по теореме Пифагора:
Равенство векторов
Через начало и конец векторов можно провести прямую. В связи с этим можно ввести понятие коллинеарных векторов.
На рисунке коллинеарны вектора а и b, так как они лежат на одной прямой. Также коллинеарны с и d, так как они лежат на параллельных прямых. А вот вектора a и c неколлинеарны, так как они лежат на пересекающихся прямых.
Для пары коллинеарных векторов можно определить, являются ли они сонаправленными или противоположно направленными.
Для обозначения сонаправленных векторов используется символ «⇈», а для противоположно направленных «⇅». Можно сформулировать две очевидных теоремы о коллинеарных векторах.
Проиллюстрируем эти правила с помощью рисунка:
Особняком стоит нулевой вектор. Он представляет собой точку, а потому не имеет определенного направления. Поэтому условно его считают сонаправленным с любым другим вектором.
Теперь мы можем дать определение равенству векторов.
Задание. Найдите на картинке равные вектора.
Решение. Здесь равны вектора а, b и e. Они сонаправлены и имеют длину 6. Вектор с сонаправлен с ними, но его длина составляет только 5 клеток. Длина вектора d составляет 6 клеток, но он не сонаправлен с другими векторами. Наконец, вектор m также не сонаправлен с другими векторами и даже не коллинеарен им.
Ответ: a, b и e.
Если началом вектора является некоторая точка А, то можно сказать, что вектор отложен от точки А. Докажем важное утверждение:
Доказать его можно построением. Пусть есть вектор а и точка М. Проведем через М прямую p, параллельную вектору а. Такая прямая будет единственной. Если точка М и вектор лежат на одной прямой, то в качестве прямой p возьмем именно эту прямую. Далее от точки М можно отложить отрезки МN и МN’, длина которых будет совпадать с длиной вектора а. В результате получится два вектора,MN и MN’, один из которых будет сонаправлен с а, а другой – противоположно направленный.
Часто равные вектора, отложенные от разных точек, обозначают одной буквой. Можно считать, что это один и тот же вектор, просто приложенный к разным точкам.
Задание. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Определите, равны ли вектора:
а) Отрезки АВ и DC равны, ведь это противоположные стороны параллелограмма, по той же причине эти отрезки параллельны. Видно, что они сонаправлены, значит, вектора равны.
б) Отрезки ВС и DA параллельны и равны, но эти вектора противоположно направлены, поэтому вектора НЕ равны друг другу.
в) Точка пересечения диагоналей параллелограмма делит их пополам, поэтому длины отрезков АО и ОС одинаковы. Вектора АО и ОС лежат на одной прямой, то есть они коллинеарны. При этом они ещё и сонаправлены, поэтому АО и ОС – равные векторы.
г) Вектора АС и BD лежат на пересекающихся прямых, то есть они не коллинеарны. Этого уже достаточно, чтобы считать их НЕ равными друг другу.
Ответ: а) д; б) нет; в) да; г) нет.
Сложение векторов
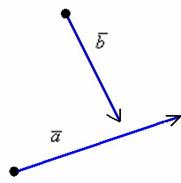
Пусть некоторый объект сначала находился в точке А, а потом переместился в точку В. Тогда его перемещение удобно обозначить с помощью вектора АВ. Далее пусть этот объект из точки В переместился в другую точку С.
С одной точки зрения, объект совершил сразу два перемещения, из А в В и из В в С, которые можно представить векторами:
Этот пример подсказывает нам универсальное правило, с помощью которого можно складывать вектора. Его называют правилом треугольника.
С помощью правила треугольника удобно складывать вектора, если конец одного из них совпадает с началом другого. Но что делать, если это не так? В этом случае достаточно от конца одного вектора отложить вектор, равный второму:
Задание. На рисунке показаны два вектора. Постройте в тетради их сумму и найдите длину получившегося вектора.
Решение. Перенесем вектор b к концу вектора а. Далее по правилу треугольника на удастся найти их сумму (обозначим этот вектор буквой с):
Теперь найдем длину получившегося вектора. Он является гипотенузой в прямоугольном треугольнике, причем длины катетов в этом треугольнике можно определить по рисунку, они составляют 4 и 6. Тогда длину гипотенузы можно найти по теореме Пифагора:
Отдельно рассмотрим случаи, когда складываются коллинеарные вектора. В этом случае получающаяся сумма окажется коллинеарной каждому слагаемому. Если вектора сонаправлены, то их длина итогового вектора окажется равной сумме длин складываемых векторов:
Если складываются противоположно направленные вектора, то длина их суммы окажется разностью длин складываемых векторов.
Именно по этой причине при решении простейших задач на движение корабля по реке скорость корабля и скорость течения либо складывают, либо вычитают. Дело в том, что в этих задачах складываются вектора скоростей корабля и течения. Когда судно плывет по течению, эти векторы сонаправлены, а когда плавание идет против течения, векторы оказываются противоположно направленными.
Задание. Корабль развивает в неподвижной воде скорость 12 км/ч. Он плывет по реке, скорость воды в которой составляет 5 км/ч. Найдите скорость корабля относительно берега, если:
а) судно плывет по течению;
б) судно плывет против течения;
в) судно плывет перпендикулярно течению.
Решение. Во всех случаях итоговая скорость судна является векторной суммой собственной скорости судна и течения реки:
Однако направления этих векторов различны. Найдем решение графически, с помощью построений. В первом случае вектора по условию сонаправлены:
Приложив другу к другу отрезки длиной 12 и 5, получим отрезок длиной 17. Это значит, что в первом случае скорость корабля относительно берега составит 17 км/ч.
Во втором случае вектора уже окажутся противоположно направленными:
Отрезок, соответствующий итоговой скорости, здесь уже равен 7 клеткам, значит, итоговая скорость составляет 7 км/ч.
В третьем случае вектора скоростей перпендикулярны:
При построении получился прямоугольный треугольник, вектор итоговой скорости в нем оказался в роли гипотенузы. Найти его длину можно по теореме Пифагора, ведь катеты нам известны:
Свойства сложения
Действия с векторами во многом подобны действиям с обычными числами. Напомним, что в алгебре при прибавлении к числу нуля оно не менялось:
Аналогично и при прибавлении к вектору нулевого вектора он не изменится:
Работает ли это правило с векторами? Оказывается, что да. Убедиться в этом можно, построив параллелограмм, сторонами которого являются складываемые векторы:
Видно, что диагональ параллелограмма является суммой векторов, которые соответствуют нижней и крайней правой его стороне. Они обозначены как векторы a и b, причем в данном случае к а прибавляется b. Но одновременно эта же диагональ – это сумма векторов, которые соответствуют крайней левой и его верхней стороне. Напомним, что противоположные стороны параллелограмма равны и параллельны, поэтому они и обозначены одним вектором. В этом случае уже к b прибавляется a. Результат при этом получается одинаковый, поэтому можно записать, что
На этом примере мы увидели, как работает ещё одно правило сложения векторов, который называется правилом параллелограмма. Если есть два вектора, которые необходимо сложить, то можно отложить их от одной точки, а потом достроить получившуюся фигуру до параллелограмма.
Задание. Сложите с помощью правила параллелограмма вектора, изображенные на рисунке:
Решение. Надо всего лишь построить параллелограмм, как показано на рисунке. Его диагональ и окажется искомым вектором:
Ещё один закон, использующийся в алгебре, называется сочетательным законом, записывается он так:
Оказывается, что и при действиях с векторами он также работает, то есть справедливо соотношение:
Здесь оранжевый вектор – это сумма красного (а) и синего (b) вектора. Если к оранжевому вектору добавить зеленый (с), то получится фиолетовый вектор, который, таким образом, является суммой
Желтый вектор – это сумма синего и зеленого вектора. Видно, что фиолетовый вектор представляет собой сумму красного и желтого, то есть он представляет сумму
Складывать можно любое количество векторов. В этом случае надо последовательно прикладывать эти вектора друг к другу, выстраивая «цепочку» векторов. Например, сложение 4 векторов, показанных на рисунке, будет осуществляться следующим образом:
Этот способ сложения векторов именуют правилом многоугольника. Естественно, в силу переместительного закона вектора можно прикладывать друг к другу в разной последовательности, при этом результат будет получаться один и тот же.
Задание. Сложите, используя правило многоугольника, вектора, изображенные на рисунке. Выполните сложение двумя разными способами:
В первом случае последовательно сложим вектора a, b, c и d. Во втором случае изменим последовательность сложения. Например, сложим их в порядке d, b, c, a:
Видно, что каждый из двух способов дал один и тот же результат, что ещё раз подтверждает справедливость переместительного закона сложения векторов.
Вычитание векторов
Напомним, что в алгебре операция вычитания вводится как операция обратная сложению. То есть если для трех чисел верно соотношение
то разностью чисел с и a как раз окажется b:
Аналогично вычитание понимается и в векторной алгебре. Пусть построены вектора а, b и c так, что
Этот пример показывает, как строить разность двух векторов. На рисунке вектора с и a отложены от одной точки, а вектор b, являющийся их разницей, проведен от конца вычитаемого вектора к концу уменьшаемого вектора.
В данном случае под уменьшаемым вектором понимается тот, который в разнице стоит перед знаком минус, а вычитаемый вектор – тот, который находится уже после этого знака. Например, в записи
Вектор а – уменьшаемый, а вектор b – вычитаемый.
Задание. Постройте в тетради разность векторов, изображенных на рисунке:
Решение. Заметим, что в условии не сказано, какой вектор из какого надо вычитать. Поэтому можно построить сразу два ответа:
Несложно заметить, две получившиеся разности представляют собой противоположно направленные векторы одной длины. Такие векторы называются противоположными.
Очевидно, что если сложить друг с другом два противоположных вектора, то получится нулевой вектор:
Противоположные вектора играют в векторной алгебре такую же роль, как и противоположные числа. С их помощью удобно выполнять вычитание векторов. Напомним, что для обычных чисел справедливо соотношение:
Поэтому операцию вычитания можно заменить операцией сложения, если вместо вычитаемого вектора взять вектор, противоположный ему. Рассмотрим этот способ на примере. Пусть из a надо вычесть b:
На первом шаге надо построить вектор, противоположный b:
Теперь надо просто сложить a и (– b):
В итоге нам удалось построить разность векторов а и b.
Умножение вектора на число
Предположим, что нам надо сложить два равных вектора. В результате мы получим новый вектор, который будет сонаправлен с исходным, но его длина будет вдвое больше. Логично считать, что получившийся вектор вдвое больше исходного, то есть он получился при умножении вектора на число 2:
Аналогично можно построить вектора, которые больше исходного не в 2, а в 3,4 и т. д. раз:
Итак, чтобы умножить вектор на положительное число k, надо построить сонаправленный с ним вектор, длина которого в k раз больше.А как умножать вектор на отрицательное число? Здесь нужно использовать противоположный вектор. Логично считать, что он получается при умножении (– 1) на вектор. Зная это, легко умножать вектор и на другие отрицательные числа:
Естественно, что если вектор умножается на ноль, то в результате получается нулевой вектор.
Задание. На рисунке показаны вектора а и b. Найдите вектора
Решение. Для построения снам надо сначала умножить исходные вектора на 4 и 2, а далее полученные результаты сложить:
Для нахождения вектора d надо построить вектор, противоположный вектору 2b, и уже его складывать с 4a:
Наконец, для нахождения вектора е необходимо построить противоположный вектор уже для 4а:
Некоторые правила обычной алгебры, касающиеся операции умножения, справедливы и для векторов. Первый такое правило – это сочетательный закон:
Видно, что мы можем либо сразу умножить вектор а на число 12, либо сначала его умножить на 4, а потом на 3. Результат операции при этом не изменится.
Также в отношении операции умножения векторов на число справедлив распределительный закона, которые позволяют раскрывать скобки:
Например, пусть нам надо сложить вектора 2а и 3а. Распределительный закон говорит, что мы можем поступить двумя способами. В первом случае мы просто строим вектора 2а и 3а и складываем их. Во втором случае мы складываем только числа 2 и 3 (получаем 5), и далее уже умножаем вектор а на число 5:
Есть ещё один распределительный закон, в котором в скобках находится уже сумма векторов, а не чисел:
Этот закон можно применить в случае, когда нам необходимо, например, сложить вектора 4а и 4b. Конечно, можно просто построить их и сложить, однако закон говорит, что мы можем сначала сложить aи b, и уже потом эту сумму умножить на 4:
Сформулированные нами законы сложения и умножения векторов позволяют выполнять действия с векторами так же, как с числами. В том числе можно упрощать выражения, содержащие векторные величины. Например, пусть известны вектора а, b и с, и надо найти вектор
Видно, что выражение значительно упростилось.
Решение задач с помощью векторов
Вектора активно используются в физике при решении многих задач, однако они также помогают доказывать геометрические теоремы. Рассмотрим несколько примеров, и начнем со вспомогательной задачи.
Задание. Известно, что С – это середина отрезка АВ. Докажите, что для любой точки О выполняется равенство:
Используя правило треугольника, вектор ОС можно представить в виде двух различных сумм:
Проанализируем выражение в скобках. Вектора АС и ВС коллинеарны, ведь они лежат на одной прямой АВ. При этом они противоположно направлены. Длина у них одинакова, ведь С – середина АВ. Тогда по определению АС и ВС – противоположные вектора, и их сумма равна нулю:
Задание. Докажите, что если в трапеции провести прямую, проходящую через середины ее оснований, то она также пройдет через точку, в которой пересекаются продолжения боковых сторон трапеции.
Решение. Построим трапецию, обозначим ее вершины и середины оснований:
Здесь ABCD – трапеция, основаниями которой являются отрезки ВС и AD. M и N – их середины. Прямые АВ и CD пересекаются в точке O. Необходимо доказать, что прямая MN также проходит через О.
Заметим, что ∆ОВС и ∆ОАD подобны. Действительно, у них есть общий ∠ВОС, а ∠ОВС и ∠ОАD одинаковы как односторонние углы при секущей АВ, поэтому треугольники подобны по 1-ому признаку. Обозначим коэффициент подобия буквой k, тогда можно записать, что
Так как отрезки ОА и АВ лежат на одной прямой, то вектора ОА и АВ коллинеарны и притом сонаправлены, поэтому в (1) отрезки можно заменить векторами:
(это соотношение мы доказали в предыдущей, вспомогательной задаче).
Аналогичную формулу можно составить и для второго основания и его середины N:
Полученное нами равенство означает, что вектора ON и ОМ коллинеарны, а значит, лежат на одной прямой (эти вектора не могут лежать на параллельных прямых, так как имеют общую точку О). Тогда получается, что О, M и N лежат на одной прямой, ч. т. д.
Векторы для чайников. Действия с векторами.
Координаты вектора. Простейшие задачи с векторами
Наконец-то у меня добрались руки до обширной и долгожданной темы аналитической геометрии. Сначала немного о данном разделе высшей математики…. Наверняка вам сейчас вспомнился курс школьной геометрии с многочисленными теоремами, их доказательствами, чертежами и т.д. Что скрывать, нелюбимый и часто малопонятный предмет для значительной доли учеников. Аналитическая геометрия, как ни странно, может показаться более интересной и доступной. Что означает прилагательное «аналитическая»? На ум сразу приходят два штампованных математических оборота: «графический метод решения» и «аналитический метод решения». Графический метод, понятно, связан с построением графиков, чертежей. Аналитический же метод предполагает решение задач преимущественно посредством алгебраических действий. В этой связи алгоритм решений практически всех задач аналитической геометрии прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.
Открываемый курс уроков по геометрии не претендует на теоретическую полноту, он ориентирован на решение практических задач. Я включу в свои лекции только то, что с моей точки зрения, является важным в практическом плане. Если вам необходима более полная справка по какому-либо подразделу, рекомендую следующую вполне доступную литературу:
1) Вещь, с которой, без шуток, знакомо несколько поколений: Школьный учебник по геометрии, авторы – Л.С. Атанасян и Компания. Сия вешалка школьной раздевалки уже выдержала 20 (!) переизданий, что, конечно, не является пределом.
2) Геометрия в 2 томах. Авторы Л.С. Атанасян, Базылев В.Т. Это литература для высшей школы, вам потребуется первый том. Из моего поля зрения могут выпадать редко встречающиеся задачи, и учебное пособие окажет неоценимую помощь.
Из инструментальных средств предлагаю собственную разработку – программный комплекс по аналитической геометрии, который значительно упростит жизнь и сэкономит массу времени.
Предполагается, что читатель знаком с базовыми геометрическими понятиями и фигурами: точка, прямая, плоскость, треугольник, параллелограмм, параллелепипед, куб и т.д. Желательно помнить некоторые теоремы, хотя бы теорему Пифагора, привет второгодникам)
А сейчас мы последовательно рассмотрим: понятие вектора, действия с векторами, координаты вектора. Далее рекомендую прочитать важнейшую статью Скалярное произведение векторов, а также Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов. Не лишней будет и локальная задача – Деление отрезка в данном отношении. На основе вышеуказанной информации можно освоить уравнение прямой на плоскости с простейшими примерами решений, что позволит научиться решать задачи по геометрии. Также полезны следующие статьи: Уравнение плоскости в пространстве, Уравнения прямой в пространстве, Основные задачи на прямую и плоскость, другие разделы аналитической геометрии. Естественно, попутно будут рассматриваться типовые задания.
Более того, по материалам сайта создана книга!
. да, это свершилось! – освойте азы теории и научитесь решать в кратчайшие сроки! Спасибо за поддержку проекта.
Понятие вектора. Свободный вектор
Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец: 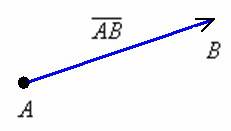
В данном случае началом отрезка является точка 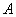
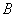
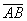
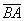
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором 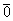
. Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.
Обозначения: Многие сразу обратили внимание на палочку без стрелочки в обозначении 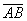
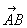
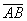
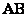
То была стилистика, а сейчас о способах записи векторов:
1) Векторы можно записать двумя большими латинскими буквами:
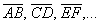
2) Векторы также записывают маленькими латинскими буквами:
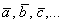
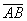
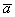
Длиной или модулем ненулевого вектора 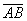
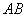
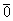
Длина вектора обозначается знаком модуля: 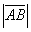
Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.
То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.
Если совсем просто – вектор можно отложить от любой точки:
Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР или свободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной «школьный» вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте направленный отрезок произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ. Есть такая студенческая присказка: Каждому лектору в ж**у по вектору. Ведь не просто остроумная рифма, всё почти корректно – направленный отрезок можно пристроить и туда. Но не спешите радоваться, чаще страдают сами студенты =)
Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора, данное в начале параграфа: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.
Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.
Действия с векторами. Коллинеарность векторов
В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.
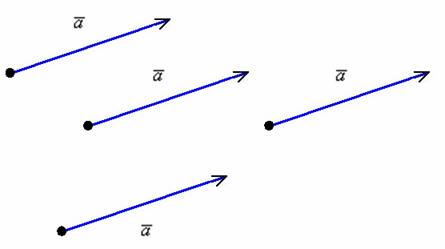
Правило сложения векторов по правилу треугольников
Рассмотрим два произвольных ненулевых вектора 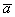
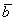
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор 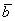
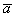
Суммой векторов 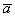
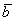
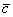
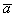
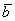
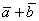
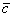
Кстати, если вектор 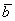
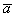
Умножение вектора на число
Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».
Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.
Обозначения: коллинеарность векторов записывают привычным значком параллельности: 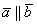
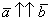
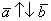
Произведением ненулевого вектора 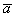
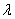
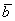
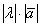
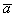
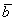
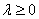
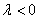
Правило умножения вектора на число легче понять с помощью рисунка:
Разбираемся более детально:
1) Направление. Если множитель 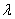
2) Длина. Если множитель заключен в пределах 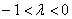
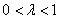
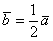
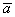
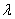
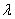
3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например, 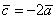
4) Векторы 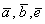
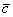
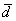
Какие векторы являются равными?
Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».
С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.
Координаты вектора на плоскости и в пространстве
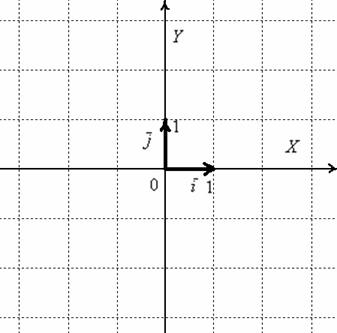
Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы 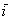
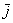
Векторы 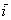
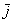
Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например: 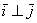
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Что такое базис, думаю, интуитивно многим понятно, более подробную информацию можно найти в статье Линейная (не) зависимость векторов. Базис векторов. Простыми словами, базис и начало координат задают всю систему – это своеобразный фундамент, на котором кипит полная и насыщенная геометрическая жизнь.
Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице.
Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: 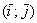
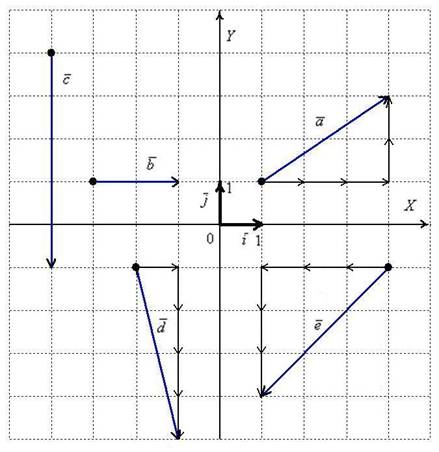
Любой вектор 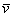
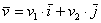
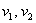
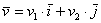
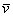
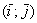
! ВСЕМ настоятельно рекомендую прочитать ВСЁ!
Начнем с первой буквы алфавита: 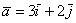
1) правило умножения вектора на число: 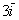
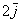
2) сложение векторов по правилу треугольника: 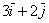
А теперь мысленно отложите вектор 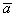
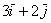
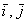
Векторы 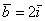
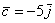
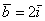
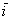
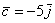
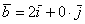
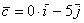
А базисные векторы, к слову, так: 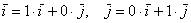
И, наконец: 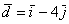
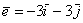
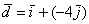
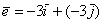
Рассмотренное разложение вида 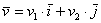
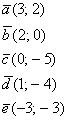
Сами базисные векторы записываются так: 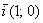
То есть, в круглых скобках указываются координаты вектора. В практических задачах используются все три варианта записи.
Сомневался, говорить ли, но всё-таки скажу: координаты векторов переставлять нельзя. Строго на первом месте записываем координату, которая соответствует единичному вектору 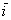
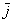
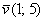
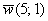
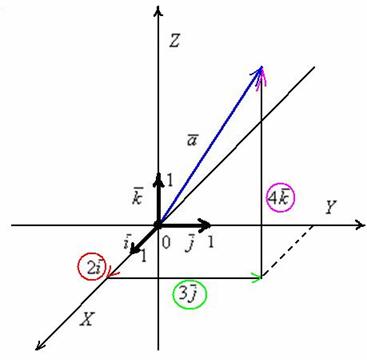
С координатами на плоскости разобрались. Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так же! Только добавится ещё одна координата. Трехмерные чертежи выполнять тяжко, поэтому ограничусь одним вектором, который для простоты отложу от начала координат:
Перед вами ортонормированный базис 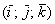
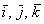
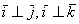
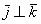
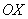
Любой вектор 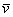
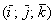
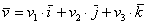
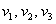
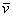
Пример с картинки: 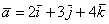
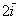
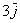
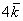
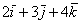
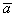
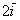
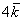
Все векторы трехмерного пространства, естественно, тоже свободны, попробуйте мысленно отложить вектор 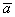
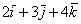
Аналогично плоскому случаю, помимо записи 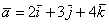
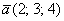
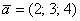
Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры:
вектор 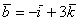
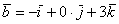
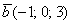
вектор 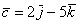
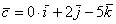
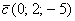
вектор 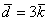
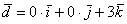
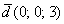
Базисные векторы записываются следующим образом:
Вот, пожалуй, и все минимальные теоретические знания, необходимые для решения задач аналитической геометрии. Возможно многовато терминов и определений, поэтому чайникам рекомендую перечитать и осмыслить данную информацию ещё раз. Да и любому читателю будет полезно время от времени обращаться к базовому уроку для лучшего усвоения материала. Коллинеарность, ортогональность, ортонормированный базис, разложение вектора – эти и другие понятия будут часто использоваться в дальнейшем. Отмечу, что материалов сайта недостаточно для сдачи теоретического зачета, коллоквиума по геометрии, так как все теоремы (к тому же без доказательств) я аккуратно шифрую – в ущерб научному стилю изложения, но плюсом к вашему пониманию предмета. Для получения обстоятельной теоретической справки прошу следовать на поклон к профессору Атанасяну.
А мы переходим к практической части:
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть, даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.
Как найти вектор по двум точкам?
Если даны две точки плоскости 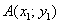
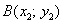
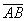
Если даны две точки пространства 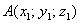
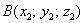
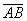
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Задание: Для тех же точек запишите формулы нахождения координат вектора 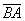
Даны две точки плоскости 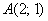
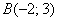
Решение: по соответствующей формуле:
Как вариант, можно было использовать следующую запись:
Эстеты решат и так:
Лично я привык к первой версии записи.
Ответ:
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь:
Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису 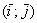
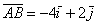
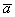
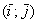
Записи координат точек и координат векторов вроде бы схожи: 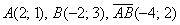
Дамы и господа, набиваем руку:
а) Даны точки 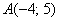
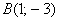
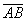
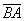
б) Даны точки 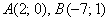
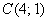
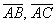
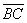
в) Даны точки 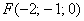
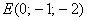
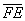
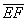
г) Даны точки 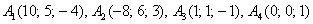
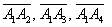
Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится ;-). Чертежи делать не нужно. Решения и ответы в конце урока.
Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =)
Как найти длину отрезка?
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости 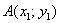
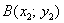
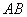
Если даны две точки пространства 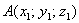
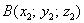
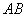
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: 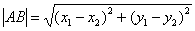
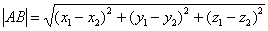
Даны точки 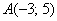
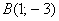
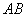
Решение: по соответствующей формуле:
Ответ:
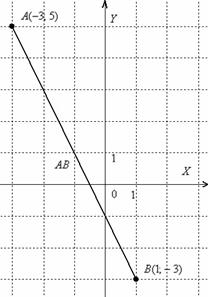
Для наглядности выполню чертёж
Отрезок 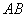
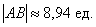
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня. В результате вычислений у нас получился результат 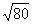
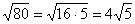
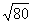
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например 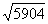
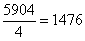
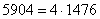
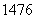
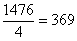
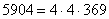
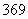
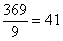
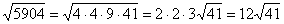
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Даны точки 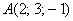
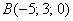
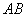
Решение и ответ в конце урока.
Как найти длину вектора?
Если дан вектор плоскости 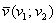
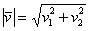
Если дан вектор пространства 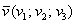
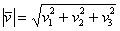
Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.
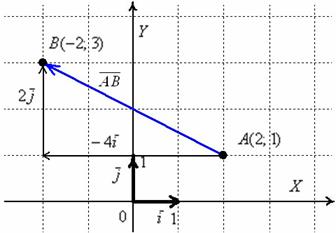
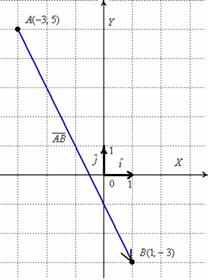
Даны точки 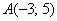
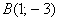
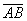
Я взял те же точки, что и в Примере 3.
Решение: Сначала найдём вектор 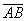
По формуле 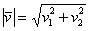
Ответ:
Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3 знаков после запятой.
Выполним чертеж к задаче:
В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости, при этом его лучше переобозначить, например, через 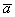
А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка 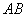
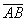
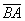
Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки 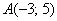
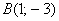
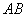
Вместо применения формулы 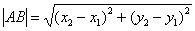
1) Находим вектор 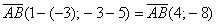
2) А теперь ссылаемся на то, что длина отрезка 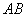
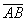
Этот способ широко практикуется в ходе решений задач аналитической геометрии.
Вышесказанное справедливо и для пространственного случая
а) Даны точки 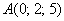
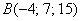
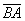
б) Даны векторы 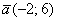
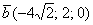
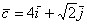
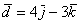
Решения и ответы в конце урока.
Действия с векторами в координатах
В первой части урока мы рассматривали правила сложения векторов и умножения вектора на число. Но рассматривали их с принципиально-графической точки зрения. Посмотрим, как данные правила работают аналитически – когда заданы координаты векторов:
1) Правило сложения векторов. Рассмотрим два вектора плоскости 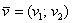
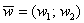
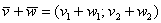
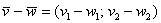
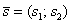
Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы 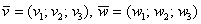
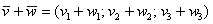
2) Правило умножения вектора на число. Ещё проще! Для того чтобы вектор 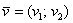
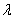
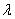
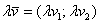
Для пространственного вектора 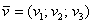
Приведённые факты строго доказываются в курсе аналитической геометрии.
Примечание: Данные правила справедливы не только для ортонормированных базисов 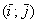
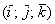
Даны векторы 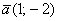
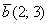
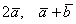
Решение чисто аналитическое:
Ответ:
Чертеж в подобных задачах строить не надо, тем не менее, геометрическая демонстрация будет весьма полезной. Если считать, что векторы заданы в ортонормированном базисе 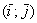
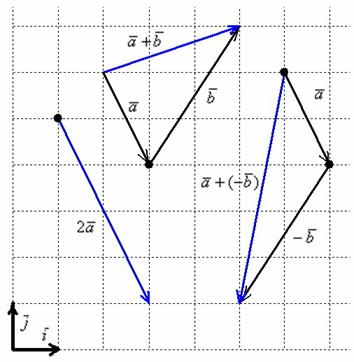
Коль скоро речь идет только о векторах в ортонормированном базисе, то оси рисовать не обязательно. Достаточно начертить базисные векторы, причём, где угодно. Ну, и координатную сетку для удобства. Строго говоря, ранее я допустил небольшой огрех – в некоторых чертежах урока тоже можно было не чертить декартову прямоугольную систему координат. Векторам она не нужна, им нужен базис. Впрочем, лучше всегда рисуйте, а то напугаете всех своими знаниями =)
Как видите, графический способ решения привёл к тем же результатам, что и аналитический способ решения. Ещё раз заметьте свободу векторов: любую из трёх «конструкций» можно переместить в любую точку плоскости.
Для векторов в пространстве можно провести аналогичные выкладки. Но там чертежи строить значительно сложнее, поэтому ограничусь аналитическим решением (на практике, собственно, бОльшего и не надо):
Даны векторы 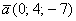
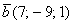
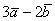
Решение: Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:
Ответ:
И в заключение занятный пример с векторами на плоскости:
Даны векторы 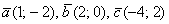
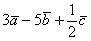
Это задача для самостоятельного решения.
Какой вывод? Многие задачи аналитической геометрии прозрачны и просты, главное, не допустить вычислительных ошибок. Следующие рекомендуемые к изучению уроки:
Это, так скажем, вектор-минимум студента =)
Любите векторы, и векторы полюбят вас!
Задание: 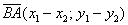
Пример 2: Решение:
а) 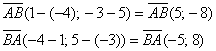
б) 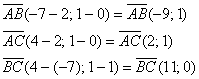
в) 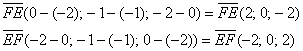
г)
Пример 4: Решение:
По соответствующей формуле: 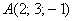
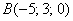
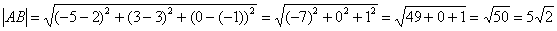
Ответ:
Пример 6: 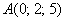
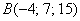
а) Решение: найдём вектор 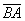
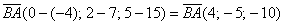
Вычислим длину вектора: 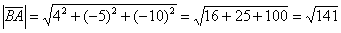
Ответ:
б) Решение:
Вычислим длины векторов:
Пример 9: Решение: 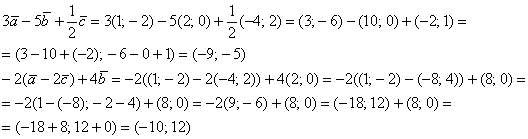
Примечание: Перед выполнением действий можно предварительно раскрыть скобки:
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5