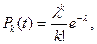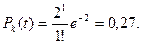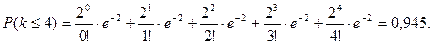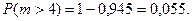Чем занимается теория массовых очередей
Теория очередей
Многие экономические задачи связаны с системами массового обслуживания, в которых происходит удовлетворение требований на выполнение каких-либо услуг.
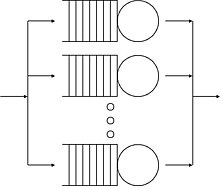
Исследованием систем массового обслуживания (СМО) занимается теория очередей, на начальное развитие которой оказали особое влияние труды датского ученого А.К. Эрланга (1878-1929) в области проектирования и эксплуатации телефонных станций. Общая схема СМО показана на рис.1.
 | ||||
 | ||||
 | | | ||
 | ||||
 |  |  | ||
 |  |  |  |  |
Входной Правило Правило Каналы Выходной
поток постановки Очередь обслуживания обслуживания поток
требований в очередь требований
Требование на обслуживание (например, неисправный автомобиль, судно) поступает в обслуживающую систему (автомастерскую, порт). Если есть свободные каналы обслуживания (мастера, причалы), то требование выполняется. Если все каналы заняты, то требование ставится в очередь по определенным правилам или покидает систему не обслуженным.
Основная задача теории массового обслуживаниясводится к определению оптимального соотношения между входным потоком требований и числом обслуживающих каналов, при котором общие суммарные затраты минимальны.
Общие суммарные затраты складываются из затрат обслуживания и затрат ожидания, причем по мере увеличения сервиса затраты обслуживания увеличиваются, а затраты ожидания уменьшаются.
СМО можно описать, задавая следующие ее компоненты:
· входной поток требований,
Входной поток требований характеризуется вероятностным законом распределения моментов поступления требований в систему и количеством требований в каждом поступлении.
В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач теории очередей, в которых поток требований является простейшим (пуассоновским).
Простейший поток событий обладает тремя свойствами:
1. стационарностью – постоянным количеством событий в единицу времени;
2. отсутствием последействия – независимостью количества событий после любого момента времени от количества событий до него;
3. ординарностью – практической невозможностью одновременного поступления нескольких требований.
Для простейшего потока частота наступления событий подчиняется закону Пуассона, то есть вероятность того, что за время t произойдет k событий, определяется:
где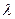 
— количество событий в единицу времени (интенсивность потока).
Вероятность того, что один причал занят (k=1) при отказе в среднем в единицу времени двух причалов (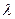=2):
Вероятность того, что все причалы свободны – 13%; вероятность того, что один причал занят – 27%; два – 27%; три – 18%; четыре – 9% и т.д.
По теореме сложения вероятностей, вероятность суммы независимых событий равна сумме вероятностей этих событий, отсюда вероятность отказа в единицу времени не более четырех причалов равна сумме вероятностей отсутствия отказа и вероятностей отказа одной, двух, трех, четырех причалов:
Вероятность отказа более четырех причалов:
Дисциплина очереди описывает порядок обслуживания требований в системе. Длина очереди может быть ограниченной или неограниченной. Правила постановки в очередь: FIFO– «первым пришел первым обслуживаешься», LIFO– «последним пришел первым обслуживаешься», по другим приоритетам или случайно.
Механизм обслуживания характеризуется продолжительностью процедур обслуживания и количеством одновременно обслуживаемых требований.
Время обслуживания требований в системе является случайной величиной и обычно описывается экспоненциальным законом распределения, то есть распределение длительности оставшейся части работ по обслуживанию не зависит от того, сколько оно уже продолжалось.
Вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой:
,
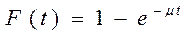
где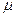 
— величина, обратная среднему времени обслуживания.
Введем в рассмотрение параметр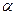 
— коэффициент загрузки системы или среднее число каналов (причалов), которые необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования (суда):
,
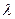
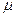
где — среднее число требований, поступающих в единицу времени; (интенсивность входного потока)
— среднее число требований, удовлетворяемых в единицу времени; (интенсивность потока обслуживания)
Тобс – среднее время обслуживания одним каналом одного требования.
Заметим, что, если 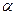меньше количества каналов обслуживания, то очередь не может расти безгранично, то есть число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования.
Различают следующие виды СМО. В зависимости от условий ожидания требованием начала обслуживания различают СМО с отказами и с ожиданием.
В системах с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и утрачиваются.
В системах с ожиданием требование, застав все обслуживающие каналы занятыми, ставится на очередь вплоть до освобождения любого из каналов.
СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ожиданием и ограниченной длиной очереди.
СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.
СМО, допускающие очередь, но с ограниченным числом циркулирующих в системе требований, называются системами с ограниченным потоком требований.
По числу каналов обслуживания различают одноканальные и многоканальные системы.
По числу фаз обслуживания – однофазные и многофазные (последовательная обработка требований на нескольких каналах).
В жизни почти всегда бывает так, что человек, владеющий разными инструментами (по своей профессии) и применяющий их в зависимости от характера выполняемой работы, добивается лучших результатов, чем человек, владеющий лишь универсальным приемом.
В одних случаях можно выполнить вычисления устно, в других – необходим лист бумаги для расчетов, в-третьих – расчет на компьютере, в-четвертых – привлечение специальной программы оптимизационных расчетов.
Нужно знать и уметь пользоваться универсальными и частными приемами, которые ведут к цели быстрее и легче.
Афоризмы классиков математического моделирования:
Математика имеет хороший инструмент. Экономика обладает хорошим материалом. Экономико-математические методы – это совмещение хорошего инструмента с хорошим исходным материалом.
СОДЕРЖАНИЕ
Написание
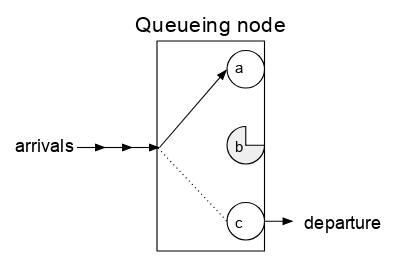
Одиночные узлы очередей
Процесс рождения-смерти
Уравнения баланса
Первые два уравнения подразумевают
По математической индукции
Обозначения Кендалла
Одиночные узлы очередей обычно описываются с использованием нотации Кендалла в форме A / S / c, где A описывает распределение продолжительности между каждым поступлением в очередь, S распределение времени обслуживания для заданий и c количество серверов в узле. В качестве примера обозначения очередь M / M / 1 представляет собой простую модель, в которой один сервер обслуживает задания, которые поступают в соответствии с процессом Пуассона (где длительность между поступлениями распределяется экспоненциально ) и имеют экспоненциально распределенное время обслуживания (M обозначает марковский процесс ). В очереди M / G / 1 G означает «общий» и указывает произвольное распределение вероятностей для времени обслуживания.
Пример анализа очереди M / M / 1
Рассмотрим очередь с одним сервером и следующими характеристиками:
Когда система переходит в установившееся состояние, скорость прибытия должна быть равна скорости отправления.
Таким образом, уравнения баланса
Простая очередь с двумя уравнениями
Предполагая экспоненциальное распределение ставок, время ожидания W можно определить как долю обслуженных прибывших. Это равно экспоненциальной выживаемости тех, кто не бросает учебу в течение периода ожидания, что дает:
Второе уравнение обычно переписывается как:
Двухэтапная модель одного блока широко распространена в эпидемиологии.
Обзор развития теории
Если на узле больше заданий, чем серверов, то задания будут стоять в очереди и ждать обслуживания.
Системы со связанными орбитами являются важной частью теории массового обслуживания в приложениях к беспроводным сетям и обработке сигналов.
Сервисные дисциплины
На узлах очередей могут использоваться различные политики планирования:
Сбои сервера происходят в соответствии со случайным процессом (обычно Пуассоном) и сопровождаются периодами настройки, в течение которых сервер недоступен. Прерванный клиент остается в зоне обслуживания до тех пор, пока сервер не будет отремонтирован.
Необслуживаемые прибывающие клиенты (либо из-за того, что очередь не имеет буфера, либо из-за отказа или отказа со стороны клиента) также известны как отсевы, а средний коэффициент отсева является важным параметром, описывающим очередь.
Сети массового обслуживания
Алгоритмы маршрутизации
Пределы среднего поля
Модели среднего поля рассматривают предельное поведение эмпирической меры (пропорции очередей в разных состояниях), когда количество очередей ( m выше) стремится к бесконечности. Влияние других очередей на любую данную очередь в сети аппроксимируется дифференциальным уравнением. Детерминированная модель сходится к тому же стационарному распределению, что и исходная модель.
Приближение интенсивного движения / диффузии
Пределы жидкости
Жидкие модели являются непрерывными детерминированными аналогами сетей массового обслуживания, полученными путем принятия предела, когда процесс масштабируется во времени и пространстве, что позволяет использовать неоднородные объекты. Эта масштабированная траектория сходится к детерминированному уравнению, которое позволяет доказать устойчивость системы. Известно, что сеть массового обслуживания может быть стабильной, но иметь нестабильный предел текучей среды.
Программные сетевые службы
Теория массового обслуживания
Содержание
История
Теорию потока однородных событий, которая легла в основу теории массового обслуживания, разработал советский математик А. Я. Хинчин. [2]
Первые задачи ТМО (Теории Массового Обслуживания) были рассмотрены сотрудником Копенгагенской телефонной компании, ученым Агнером Эрлангом, в период между 1908 и 1922 годами. Стояла задача упорядочить работу телефонной станции и заранее рассчитать качество обслуживания потребителей в зависимости от числа используемых устройств.
Имеется телефонный узел (обслуживающий прибор), на котором телефонистки время от времени соединяют отдельные номера телефонов друг с другом. Системы массового обслуживания (СМО) могут быть двух видов: с ожиданием и без ожидания (то есть с потерями). В первом случае вызов (требование, заявка), пришедший на станцию в момент, когда занята нужная линия, остается ждать момента соединения. Во втором случае он «покидает систему» и не требует забот СМО.
Поток
Однородный поток
Поток заявок однороден, если:
Поток без последействия
Поток без последействия, если число событий любого интервала времени (
, 
) не зависит от числа событий на любом другом непересекающемся с нашим (, ) интервале времени.
Стационарный поток
Поток заявок стационарен, если вероятность появления n событий на интервале времени (, ) не зависит от времени , а зависит только от длины этого участка.
Простейший поток
Однородный стационарный поток без последействий является простейшим, потоком Пуассона.
Число 
событий такого потока, выпадающих на интервал 
, распределено по Закону Пуассона:
Пуассоновский поток заявок удобен при решении задач ТМО. Строго говоря простейшие потоки редки на практике, однако многие моделируемые потоки допустимо рассматривать как простейшие.
Мгновенная плотность
Мгновенная плотность (интенсивность) потока равна пределу отношения среднего числа событий, приходящихся на элементарный интервал времени (, ) к длине интервала (), когда последний стремится к нулю.
или, для простейшего потока,
где 
равно математическому ожиданию числа событий на интервале .
Формула Литтла
Среднее число заявок в системе равно произведению интенсивности входного потока на среднее время пребывания заявки в системе.
Литература
Библиография
См. также
Полезное
Смотреть что такое «Теория массового обслуживания» в других словарях:
теория массового обслуживания — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] теория массового обслуживания Раздел исследования операций, который рассматривает разнообразные процессы в экономике, а также в телефонной связи, здравоохранении и других… … Справочник технического переводчика
Теория массового обслуживания — [theory of waiting lines, queueing theory] раздел исследования операций, который рассматривает разнообразные процессы в экономике, а также в телефонной связи, здравоохранении и других областях как процессы обслуживания, т.е. удовлетворения каких… … Экономико-математический словарь
Теория массового обслуживания — [theory of waiting lines, queueing theory] раздел исследования операций, который рассматривает разнообразные процессы в экономике, а также в телефонной связи, здравоохранении и других областях как процессы обслуживания, т.е. удовлетворения каких… … Экономико-математический словарь
ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ — раздел прикладной математики, применяющийся в качестве метода в экономических исследованиях. Эта теория изучает статистические закономерности в массовых операциях, состоящих из большого числа однородных элементарных операций. К ним относятся,… … Большой экономический словарь
ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ — раздел теории вероятностей, изучающей потоки требований на обслуживание, поступающие в системы обслуживания и выходящие из них, длительности ожидания и длины очередей и т. п. Целью исследований в Т. м. о. является рациональный выбор структуры… … Энциклопедический словарь по психологии и педагогике
Массового обслуживания теория — математическая дисциплина, изучающая системы, предназначенные для обслуживания массового потока требований случайного характера (случайными могут быть как моменты появления требований, так и затраты времени на их обслуживание). Типичным… … Большая советская энциклопедия
МАССОВОГО ОБСЛУЖИВАНИЯ ТЕОРИЯ — теория очередей, раздел теории вероятностей, изучающий математич. модели разного рода реальных массового обслуживания систем. Эти модели представляют собой случайные процессы специального вида, к рые наз. иногда процессами обслуживания. Чаще… … Математическая энциклопедия
МАССОВОГО ОБСЛУЖИВАНИЯ ТЕОРИЯ — раздел математики, изучающий системы, предназначенные для обслуживания массового потока требований случайного характера. Типичный пример такой системы автоматическая телефонная станция, где случайным образом поступают требования вызовы абонентов … Большой Энциклопедический словарь
массового обслуживания теория — раздел математики, изучающий системы, предназначенные для обслуживания массового потока требований случайного характера. Типичный пример такой системы автоматическая телефонная станция, где случайным образом поступают «требования» вызовы… … Энциклопедический словарь
Теория массового обслуживания
СОДЕРЖАНИЕ
Правописание [ править ]
Одиночные узлы очередей [ править ]
Процесс рождения-смерти [ править ]
Уравнения баланса [ править ]
Первые два уравнения подразумевают
По математической индукции
Состояние приводит к: ∑ n = 0 ∞ P n = P 0 + P 0 ∑ n = 1 ∞ ∏ i = 0 n − 1 λ i μ i + 1 = 1 <\displaystyle \sum _
Обозначения Кендалла [ править ]
Пример анализа очереди M / M / 1 [ править ]
Рассмотрим очередь с одним сервером и следующими характеристиками:
Когда система переходит в установившееся состояние, скорость прибытия должна быть равна скорости отправления.
Таким образом, уравнения баланса
Тот факт, что приводит к формуле геометрического распределения P 0 + P 1 + ⋯ = 1 <\displaystyle P_<0>+P_<1>+\cdots =1>
Простая очередь с двумя уравнениями [ править ]
Предполагая экспоненциальное распределение ставок, время ожидания W можно определить как долю обслуженных прибывших. Это равно экспоненциальной выживаемости тех, кто не бросает учебу в течение периода ожидания, что дает:
Второе уравнение обычно переписывается как:
Двухэтапная модель одного блока широко распространена в эпидемиологии. [7]
Обзор развития теории [ править ]
Если на узле больше заданий, чем серверов, то задания будут стоять в очереди и ждать обслуживания.
Системы со связанными орбитами являются важной частью теории массового обслуживания в приложениях к беспроводным сетям и обработке сигналов. [18]
Такие проблемы, как показатели производительности для очереди M / G / k, остаются открытой проблемой. [11] [13]
Дисциплины обслуживания [ править ]
На узлах очередей могут использоваться различные политики планирования:
Сбои сервера происходят в соответствии со случайным процессом (обычно Пуассоном), и за ними следуют периоды настройки, в течение которых сервер недоступен. Прерванный клиент остается в зоне обслуживания до тех пор, пока сервер не будет отремонтирован. [24]
Прибывающие не обслуживаемые клиенты (либо из-за отсутствия буфера в очереди, либо из-за отказа или отказа со стороны клиента) также известны как отсевы, а средний коэффициент отсева является важным параметром, описывающим очередь.
Сети очередей [ править ]
Алгоритмы маршрутизации [ править ]
Пределы среднего поля [ править ]
Модели среднего поля рассматривают предельное поведение эмпирической меры (доля очередей в разных состояниях), когда количество очередей ( m выше) стремится к бесконечности. Влияние других очередей на любую данную очередь в сети аппроксимируется дифференциальным уравнением. Детерминированная модель сходится к тому же стационарному распределению, что и исходная модель. [35]
Приближение интенсивного движения / диффузии [ править ]
Пределы жидкости [ править ]
Жидкие модели являются непрерывными детерминированными аналогами сетей массового обслуживания, полученными путем принятия предела, когда процесс масштабируется во времени и пространстве, что позволяет использовать неоднородные объекты. Эта масштабированная траектория сходится к детерминированному уравнению, которое позволяет доказать устойчивость системы. Известно, что сеть массового обслуживания может быть стабильной, но иметь нестабильный предел текучей среды. [38]