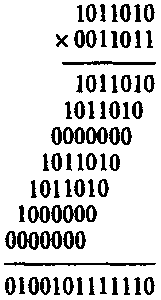Чем занимается теория сложности

Теория и практика сложности

Современный компьютер может все, но алгоритм решения какой-нибудь нехитрой задачки на триста-пятьсот переменных грубой силой может потребовать шагов больше, чем во Вселенной элементарных частиц.

Об авторе: Сергей Николенко, e-mail sergey@logic.pdmi.ras.ru, веб-сайт logic.pdmi.ras.ru/

Этой проблемой занимается теория сложности: пытается придумать алгоритмы, которые бы работали быстро, а затем доказать, что они быстро работают. Или, на худой конец, доказать, что таких алгоритмов придумать нельзя.

Немного теории

Математически есть смысл рассматривать лишь бесконечные последовательности задач: если размер входа ограничен, всякий алгоритм можно заменить большущей, но все же константного размера таблицей, в которой будет записано соответствие между входами и выходами, и алгоритм будет иметь константную сложность (и совершенно не важно, что константа эта может оказаться больше числа атомов во Вселенной).

Pro: биоинформатика

В результате каждое продвижение в теории сложности алгоритмов для нужд биоинформатики находит практическое применение: ведь зачастую входом алгоритму служит весь GenBank, и сказываются даже минимальные асимптотические улучшения.

Характер задач биоинформатики таков, что теоретические оценки, как правило, подтверждаются на практике. Но это не всегда так, и один из важнейших контрпримеров мы рассмотрим в следующем разделе.

Contra: линейное программирование

Метод эллипсоидов Хачияна стал, наверное, самым ярким примером разграничения между теоретически и практически успешными алгоритмами. Алгоритм, имеющий лучшую верхнюю оценку сложности, вовсе не обязательно будет наиболее удачен для практической реализации.

Pro et contra: выполнимость

— Из журнала «Компьютерра»

1. Алан Тьюринг, один из отцов-основателей современной computer science, заложил основы теории сложности в середине 30-х годах прошлого века, когда из компьютеров (то есть «устройств для счета») доступны были абаки, арифмометры да не доведенная до «железа» машина Бэббиджа. Возможно, без его основополагающих работ никаких компьютеров бы и не появилось. [вернуться]

2. Мы никоим образом не хотим умалить трудности сугубо биологического характера: до середины 1970-х никто и мечтать не мог о том, что такие задачи вообще возникнут, и современное положение дел создано в первую очередь руками биологов. И сейчас биологические проблемы получения и интерпретации данных для комбинаторных задач стоят очень остро, но мы сейчас сконцентрируемся на математических трудностях. [вернуться]

4. Об этом Л. В. Канторович говорил в своей Нобелевской лекции. Кстати, векторы, лежащие в ограниченном задачей многограннике, в русской терминологии до сих пор называют планами. [вернуться]

5. Как я узнал во время подготовки статьи, 29 апреля 2005 года Леонид Генрихович, в последние годы работавший в США, скоропостижно скончался. [вернуться]

7. Наш соотечественник, петербуржец Григорий Перельман уже года два как одну из них решил. Но почему-то не хочет публиковать свое решение (которое уже, по всей видимости, общепризнано) в официальных журналах, а интернет-публикации и прочие препринты для доллароносного фонда не годятся (что вполне логично). Но это, опять же, тема для совсем другого разговора. [вернуться]

8. По именам создателей: Davis, Putnam, Logemann, Loveland; их описание базовых принципов работы этого метода относится к 1968 году. [вернуться]

Источник

Теория сложности

Рассуждения о природе, возможности построения, существования и ограничениях алгоритмов, которые я привел в предыдущих главах, были по большей части «нестрогими». Я совсем не касался вопроса о возможности практического применения упоминавшихся алгоритмов. Даже в тех задачах, где существование алгоритмов и возможные способы их построения очевидны, все же может потребоваться довольно много труда для их воплощения в нечто полезное с точки зрения практического использования. Иной раз небольшая догадка или искусный ход могут в значительной степени упростить алгоритм или же многократно увеличить его быстродействие. Техническая сторона этих вопросов часто бывает очень сложна, и в последние годы в различных направлениях прилагалось много усилий в области построения, понимания и совершенствования алгоритмов — быстро растущем и развивающемся поле деятельности для пытливых умов. Мне представляется не слишком уместным углубляться здесь в тонкости подобных вопросов. Однако, существует довольно много абсолютных ограничений общего характера (известных или предполагаемых) на возможное повышение быстродействия алгоритма. Оказывается, что среди алгоритмических по своей природе задач существуют определенные классы проблем, решать которые с помощью алгоритмов несоизмеримо труднее, чем остальные. Такие задачи можно решать только с помощью очень медленных алгоритмов (или, допустим, алгоритмов, требующих чрезмерно больших ресурсов для хранения информации, и т. п.). Теория, в которой рассматриваются подобные вопросы, носит название теории сложности.

где К и r — константы, не зависящие от n. То есть N не может быть больше, чем число, кратное n в некоторой фиксированной степени.

Простой, пример задачи, безусловно относящейся к Р, — перемножение двух чисел. Чтобы объяснить это, я должен сначала описать, как число n характеризует размер двух чисел, которые надо перемножить. Мы можем принять, что оба числа представлены в двоичной записи и что n/2 — это просто количество бинарных разрядов в каждом из чисел, так что общее число цифр (то есть битов) у обоих равно n. (Если одно из чисел длиннее другого, то мы можем записать более короткое, начав с дополнительной последовательности нулей, тем самым выровняв их по длине.) Например, если n = 14, мы бы могли рассмотреть произведение

которое является, на самом деле, произведением 1011010 х 11011, но с добавленными перед более коротким числом нулями. Выполнить требуемое действие проще всего путем умножения «в столбик»:

учитывая, что в двоичной системе 0x0=0, 0x1=0, 1×0=0, 1×1=1, 0+0=0, 0+1=1, 1+0=1, 1 + 1 = 10. Число отдельных двоичных перемножений равно (n/2) х (n/2) = n 2 /4, а число отдельных двоичных сложений может доходить до n 2 /4 — n/2 (включая перенос). Это дает n 2 /2 — n/2 отдельных арифметических операций — и мы должны еще учесть несколько дополнительных логических шагов, которые задействованы в операциях переноса. Тогда общее число шагов, игнорируя члены более низкого порядка, равно по существу N = п 2 /2, что, очевидно, является полиномом[92].

В общем случае, мы полагаем «размер» n задачи из некоторого класса равным полному количеству двоичных цифр (или битов), необходимых для задания свободных входных данных в задаче указанного размера. Другими словами, для произвольного размера n задача может иметь до 2 n различных вариантов (ибо для каждой из цифр имеется две возможности — 0 или 1, — а общее количество цифр равно n), и все они должны одинаково обрабатываться алгоритмом не более, чем за N шагов.

Существует масса примеров (классов) задач, которые не «принадлежат» множеству Р. Например, чтобы вычислить 22 r для заданного натурального r, нам только для записи конечного ответа потребуется около 2 n шагов (где n — число цифр в двоичной записи r), не говоря даже о самом вычислении. Операция по вычислению 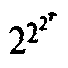потребует уже 22 n шагов для записи и так далее. Значения этих выражений намного превосходят те, которые дают полиномы для тех же n, и, следовательно, не могут принадлежать Р.

Больший интерес представляют задачи, в которых ответ может быть записан и даже проверен на верность за «полиномиальное» время. Есть очень важная категория (алгоритмически решаемых классов) проблем, обладающих таким свойством. Их называют NP—задачами (классом задач). Точнее, если некоторая задача из класса NP имеет решение, то алгоритм позволит получить это решение, которое затем может быть проверено за «полиномиальное» время. Если же задача не имеет решения, то алгоритм сообщит об этом, но при этом не оговаривается необходимость проверки этого факта за «полиномиальное» или какое бы то ни было время[93].

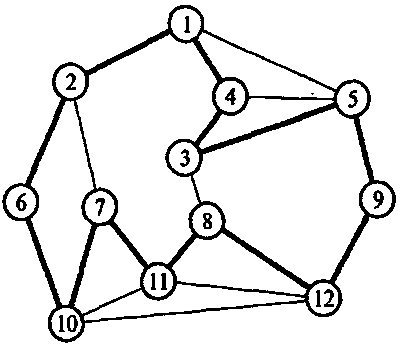
NP—задачи встречаются во многих областях, причем как в математике, так и в повседневной практике. Я приведу здесь только один простой математический пример: задачу нахождения так называемого «гамильтонова цикла» на графе (довольно устрашающее название для чрезвычайно простой идеи). Под графом подразумевается конечный набор точек, или «вершин», некоторое количество пар которых соединено между собой линиями — «сторонами» графа. (Нас не интересуют сейчас геометрические или линейные свойства, а только то, какие вершины соединяются друг с другом. Поэтому не имеет значения, лежат ли все вершины в одной плоскости — если нас не волнует возможность пересечения двух сторон — или же в трехмерном пространстве.) Гамильтонов цикл — это замкнутый маршрут (петля), состоящий только из сторон графа и проходящий не более одного раза через любую из вершин. Пример графа с изображенным на нем гамильтоновым циклом показан на рис. 4.14. Задача нахождения гамильтонова цикла заключается в том, чтобы определить, существует ли гамильтонов цикл на рассматриваемом графе, и если существует, то явным образом указать его.

Рис. 4.14. Граф с гамильтоновым циклом (изображен зачерненными линиями). Существует только один гамильтонов цикл, как читатель может сам убедиться

Есть разные способы представления графов на языке двоичных чисел. Неважно, какой из этих способов применяется в том или ином случае. Один из методов заключается в том, чтобы пронумеровать вершины 1, 2, 3, 4, 5…, а потом перечислить пары в некотором подходящем фиксированном порядке:

Затем мы на место каждой пары помещаем «1», если пара соединена стороной графа, и «О» — в противном случае. Тогда двоичная последовательность

будет означать, что вершина 1 соединяется с вершинами 2, 4 и 5; вершина 3 — с вершинами 4 и 5; вершина 4 — с вершиной 5, и т. д. (в соответствии с рис. 4.14). Гамильтонов цикл может быть задан по желанию просто как подмножество этих сторон, которое было бы описано такой же двоичной последовательностью, как и ранее, но со значительно бо?льшим числом нулей. Процедура проверки в этом случае проходит несравненно быстрее, чем процесс непосредственного построения гамильтонова цикла. Все, что нужно выяснить, — это является ли построенный цикл действительно циклом, т. е. принадлежат ли его стороны исходному графу, и что каждая вершина графа используется ровно два раза — по одному разу на концах каждой из входящих в нее двух сторон.

Такую процедуру проверки можно легко завершить за «полиномиальное» время.

На самом деле эта задача относится не только к NP, но к так называемой категории NP—полных задач. Это означает, что любая другая NP—задача может быть сведена к данной за «полиномиальное» время — так что, если бы кому-нибудь удалось отыскать алгоритм для решения задачи нахождения гамильтонова цикла за «полиномиальное» время (т. е. показать, что задача гамильтонова цикла действительно принадлежит Р), то это будет означать, что все NP—задачи будут лежать в Р! Это имело бы очень важные следствия. В широком смысле, задачи из Р считаются «податливыми» (иначе говоря, «решаемыми за приемлемое время») для относительно больших n, на быстром современном компьютере; тогда как задачи из NP, но не лежащие в Р, считаются «неподатливыми» (т. е. решаемыми в принципе, но «нерешаемыми практически») для тех же n — независимо от того, на какое разумно предсказуемое увеличение быстродействия компьютеров рассчитывать в будущем. (Реальное время, которое бы потребовалось для достаточно больших n при решении «неподатливой» задачи, легко превосходит возраст вселенной, что никак не предполагает практическое использование такого подхода!) Любой «умный» алгоритм для решения задачи о нахождении гамильтонова цикла за «полиномиальное» время мог бы быть превращен в алгоритм для решения всех прочих NP—задач, и тоже за «полиномиальное» время!

Другая задача, также являющаяся NP—полной[94] — «задача коммивояжера», которая во многом похожа на гамильтонов цикл, если не считать того, что разным сторонам приписаны числа и ставится цель отыскать гамильтонов цикл с минимальной суммой этих чисел (минимальной «длиной» пути, проделанного коммивояжером). Аналогично, «полиномиальное» время решения, достигнутое в «задаче коммивояжера», привело бы к возможности решать все NP—задачи за «полиномиальное» время. (Если такое решение когда-нибудь найдется, то новость об этом сразу попала бы на первые страницы! Ведь к NP—задачам относится, в частности, факторизация больших целых чисел, которая применяется в секретных шифровальных системах, представленных за последние несколько лет. Если эта задача окажется решаемой за «полиномиальное» время, то, возможно, такие шифры могли бы быть взломаны при помощи мощных современных компьютеров; если же нет — эти шифры останутся неприступными. См. Гарднер [1989].)

Эксперты, как правило, полагают, что используя устройство, работающее по принципу машины Тьюринга, невозможно за «полиномиальное» время решить NP—полную задачу; и что, следовательно, Р и NP — неэквивалентны. Это мнение, похоже, верно, хотя пока его никто не смог доказать. И это остается наиболее важной и на сегодняшний день нерешенной задачей теории сложности.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

§ 3. ТЕОРИЯ

§ 3. ТЕОРИЯ В науке выделяют два уровня познания — эмпирический и теоретический. На первом уровне производится сбор фактов (накопление информации об исследуемых объектах) и осуществляется первичная их систематизация в форме таблиц, схем, графиков и т.д. На эмпирическом

Теория

Теория Трудность, сформулированная в виде вопроса, представляет собой проблему. В качестве одного из вариантов решения проблемы возникает гипотеза. Обоснованная гипотеза превращается в научную теорию или в новую часть уже существовавшей ранее теории. Здесь сразу

МЕТАФИЗИЧЕСКАЯ ТЕОРИЯ БЫТИЯ И ТЕОРИЯ ПОЗНАНИЯ

МЕТАФИЗИЧЕСКАЯ ТЕОРИЯ БЫТИЯ И ТЕОРИЯ ПОЗНАНИЯ …Первичная сущность по необходимости должна быть всецело актуальной и не допускать в себе ничего потенциального. Правда, когда один и тот же предмет переходит из потенциального состояния в актуальное, по времени потенция

Некоторые сложности перевода

Некоторые сложности перевода В процессе перевода текста книги возникли определенные сложности с переводом некоторых терминов, важных для общего содержания произведения. Причины данных сложностей происходили, во-первых, из того, что некоторые используемые авторами

Тридцать одно определение сложности

Тридцать одно определение сложности Синие и красные точки, разбросанные по экрану компьютера. Но это не просто цветные точки. Это модели людей, делающие то, что делают люди: ищут пищу, ищут партнеров, соперничают и сотрудничают друг с другом. По крайней мере, так заявил

4. Ж. Лиотар: постмодерн как неуправляемое возрастание сложности

4. Ж. Лиотар: постмодерн как неуправляемое возрастание сложности Жан Франсуа Лиотар (1924—1998) опирается в своем постмодернизме на Канта, Витгенштейна, Ницше, Хайдеггера. Он является автором самого термина «постмодерн», значение которого до сих пор остается достаточно

17.5.2.3. Текучее время в физике: специальная теория относительности, общая теория относительности, квантовая механика и термодинамика

17.5.2.3. Текучее время в физике: специальная теория относительности, общая теория относительности, квантовая механика и термодинамика Беглый обзор четырех областей современной физики: специальной теории относительности (СТО), общей теории относительности (ОТО), квантовой

1. УРОВНИ СЛОЖНОСТИ ИГРЫ

1. УРОВНИ СЛОЖНОСТИ ИГРЫ Если читатель является любителем компьютерных игр или их создателем, то он наверняка знаком с таким понятием, как «уровень сложности» игры.Обычно уровнями какой-либо игры являются следующие:? дилетант («я выиграю, потому что я просто

18. Следствия теории сложности

18. Следствия теории сложности Теория сложности, утверждает, что Вселенная стремится ко все более сложным состояниям. При этом, более сложные состояния, обладают еще большим потенциалом, для развития Вселенной. Попробуем вывести несколько следствий из этой

232. ТЕОРИЯ

I. Теория интуитивизма (теория непосредственного усмотрения связи основания и следствия)

I. Теория интуитивизма (теория непосредственного усмотрения связи основания и следствия) Суждение есть акт дифференциации объекта путём сравнения. В результате этого акта, при успешном выполнении его, мы имеем предикат P, т. е. дифференцированную сторону

Теория сложности

Теория сложности Рассуждения о природе, возможности построения, существования и ограничениях алгоритмов, которые я привел в предыдущих главах, были по большей части «нестрогими». Я совсем не касался вопроса о возможности практического применения упоминавшихся

Источник

Теория сложности

Оглавление

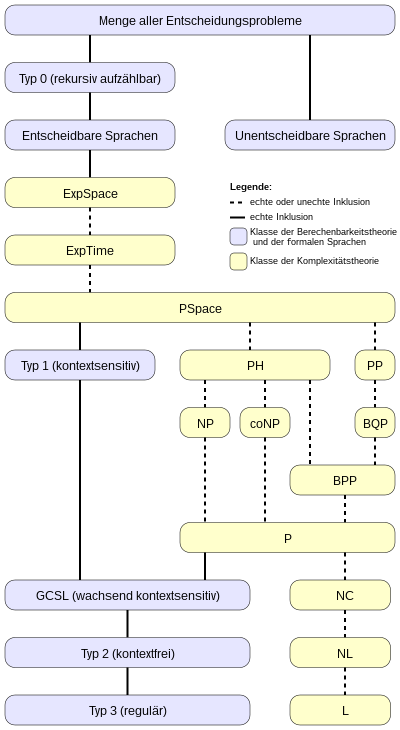
Классификация в теоретической информатике

Проблемы с точки зрения теории сложности

Проблемы принятия решений как формальные языки

Расчетные задачи в качестве иллюстраций

Помимо проблем с решением, также рассматриваются проблемы расчета. Для этого требуется ответ, описывающий решение проблемы. Например, проблема умножения обычно представляет собой проблему вычисления: вы хотите найти произведение двух чисел.

Задачи оптимизации представляют собой важную подкатегорию задач расчета.В случае задач оптимизации функциональная взаимосвязь состоит из требования определить максимум или минимум заданной функции стоимости по всем возможным решениям проблемы. В случае задачи коммивояжера необходимо было бы рассчитать длину оптимального маршрута.

Проблемные экземпляры

Проблемный экземпляр не следует путать с самой проблемой. В теории сложности проблема представляет собой общий вопрос, шаблон. Таким образом, экземпляром проблемы является полный вопрос, который определяет правильный ответ (да или нет в случае проблемы с решением).

Проблема формулируется в таком общем виде, что определяет бесконечный набор проблемных экземпляров, потому что нет смысла спрашивать о сложности конечного набора экземпляров; программа может содержать список готовых ответов и возвращать правильное решение только путем доступа к таблице, которая не отражает усилий, необходимых для определения ответов. Это становится интересным только тогда, когда существует бесконечное количество экземпляров, и вы хотите найти алгоритм, который вычисляет правильный ответ для каждого экземпляра.

Представления о проблемах

Даже если доказательства утверждений теории сложности обычно используют конкретные представления входных данных, каждый пытается сохранить утверждения и соображения независимыми от представлений. Это может быть достигнуто, например, путем обеспечения того, чтобы выбранное представление можно было, при необходимости, преобразовать в другое представление без особых усилий, без значительного изменения общих усилий по вычислению в результате. Для этого, помимо прочего, важен выбор подходящей универсальной модели станка.

Размер проблемы

После того, как проблема была формально определена (например, задача коммивояжера в форме графа с весами ребер), хотелось бы сделать утверждения о том, как алгоритм ведет себя при вычислении решения проблемы в зависимости от сложности проблемы. В целом, при оценке серьезности проблемы необходимо учитывать множество различных аспектов. Тем не менее, часто можно найти несколько скалярных величин, которые существенно влияют на поведение алгоритма в отношении потребления ресурсов. Эти размеры известны как размер проблемы. Как правило, это соответствует длине ввода (в случае специально выбранного представления ввода).

В случае задачи коммивояжера, например, размер задачи может быть определен как количество заданных местоположений (пренебрегая тем, что заданные длины маршрута также могут иметь входные переменные разных размеров). Тогда эта проблема тривиальна для задачи размера 2, поскольку здесь есть только одно возможное решение, и поэтому оно также должно быть оптимальным. Однако по мере увеличения размера проблемы алгоритм должен будет выполнять больше работы.

Лучший, худший и средний случай для размеров проблем

Функции в результатах вопросов упорядочены по возрастанию, если они четко указаны, т. Е. Это означает: проблема, которая амортизировала, например, квадратичный спрос, имеет (в лучшем случае) квадратичный спрос также в среднем, а в худшем случае не меньше.

Нижняя и верхняя оценки задач

Рассмотрение наилучшего, наихудшего и среднего случаев всегда относится к фиксированной длине ввода. Даже если рассмотрение конкретных входных длин может представлять большой интерес на практике, этот взгляд обычно недостаточно абстрактен для теории сложности. Какая длина ввода считается большой или практически актуальной, может очень быстро измениться из-за технических разработок. Поэтому оправдано исследовать поведение алгоритмов по отношению к проблеме полностью независимо от конкретной длины входных данных. С этой целью рассматривается поведение алгоритмов при постоянно увеличивающихся, потенциально бесконечно больших входных длинах. Говорят об асимптотическом поведении соответствующего алгоритма.

Напротив, доказательство верхних оценок обычно достигается путем анализа конкретных алгоритмов. Доказательство существования хотя бы одного алгоритма, удовлетворяющего верхней границе, уже обеспечивает доказательство.

Модели машин в теории сложности

Функции затрат

Стоимость меры

Модели машин и проблемы

Часто используемые модели машин

Самые распространенные модели:

Расширенная диссертация Черча-Тьюринга

Модификации модели для анализа места для хранения

Чтобы исследовать минимальные требования к памяти, которые требуются для решения проблем, в используемую модель машины (обычно машину Тьюринга) часто вносятся следующие модификации:

Внесенные изменения влияют только на поведение машины во времени с постоянным коэффициентом и, следовательно, незначительны.

Обозначения Ландау

Создание классов сложности

Влияние переменных на формирование классов сложности

На формирование классов сложности влияет ряд факторов. Основные из них следующие:

Требования к барьерным функциям

Важнейшие барьерные функции

Записи иерархии

Набор иерархии времени

Теорема об иерархии времени гласит:

Набор иерархии пространства

Теорема пространственной иерархии гласит:

К чему не применяются записи иерархии

Важные временные классы

Важные классы комнаты

Дополнение

В противоположность этому можно также рассматривать дополнение к классу K. Он содержит именно те языки / проблемы из данного базового набора, которых нет в K; эти проблемы обычно намного серьезнее, чем в K. С другой стороны, класс дополнения CoK обычно имеет непустое среднее значение с K.

Проблема P-NP и ее значение

Класс P: практически решаемые проблемы

Класс NP: задачи, поддающиеся эффективной проверке

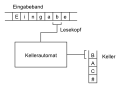
Недетерминированная машина Тьюринга может решить проблему в NP, сначала генерируя все возможные решения, в результате чего путь вычисления разветвляется на соответствующее количество путей, а затем проверяя каждое из этих решений, что может быть выполнено детерминированно, то есть без дальнейшего ветвления.

В NP есть проблемы, которые для больших экземпляров практически неразрешимы. К ним относятся NP-полные проблемы. В этом классе можно найти задачи практически из всех областей информатики. Но не все проблемы в NP сложны, потому что NP также содержит класс P.

Случай P = NP

Если бы проблема P-NP решалась в смысле P = NP, мы бы знали, что даже для NP-полных задач должны быть алгоритмы, которые работают с полиномиальными затратами времени.

И наоборот, поскольку определение NP-полноты предполагает алгоритмы, с помощью которых можно уменьшить любое количество задач от NP за полиномиальное время до NP-полных задач, с полиномиальной разрешимостью даже одной NP-полной задачи, все проблемы класс NP был бы сразу разрешим за полиномиальное время. Это приведет к тому, что вся информатика сможет решать проблемы, чего нельзя достичь даже при самых больших успехах в разработке аппаратного обеспечения.

С другой стороны, решение проблемы P-NP в смысле P = NP весьма нежелательно для некоторых приложений. Например, методы асимметричного шифрования потеряли бы большую часть безопасности, так как тогда их можно было бы разбить на полиномиальное время.

Случай P ≠ NP

Если бы проблема P-NP решалась в смысле P ≠ NP, было бы ясно, что дальнейшие попытки найти полиномиальные решения для NP-полных задач были бы бессмысленными. Легко представить, что из-за большой важности проблем в NP, попытки найти эффективное решение прекращаются только тогда, когда доказывается его невозможность. До тех пор будет по-прежнему использоваться много энергии частных и государственных исследований.

Однако сегодня во многих теоремах предполагается, что P ≠ NP, потому что только так можно проводить эффективную исследовательскую работу без доказательства равенства. Выходы ищут через приближения и эвристики, ограничения проблемы, не пренебрегающие практикой.

Последствия для теории сложности

Усилия по решению проблемы P-NP, длящиеся более тридцати лет, дают практическому компьютерному ученому высокую степень уверенности в том, что отдельные попытки эффективно решать проблемы из NP более или менее бессмысленны. Поэтому практическая информатика концентрируется на приближенных решениях или модификации исходных задач при решении задач из NP. Например, сложность алгоритмов оптимизации может быть значительно уменьшена, если человек не стремится к оптимальному решению, а удовлетворяется почти оптимальным решением. Теория сложности обеспечивает теоретическую поддержку этого подхода.

Языки и классы сложности

История теории сложности

После того, как в предыдущих разделах были объяснены многочисленные основные термины и важные результаты теории сложности, в следующих разделах дается исторический очерк, который должен помочь классифицировать хронологическую последовательность этих результатов.

Основы

Начало комплексного теоретического исследования.

Юрис Хартманис и Ричард Э. Стернс сделали первый важный шаг к такой теории в своей работе 1965 года « О вычислительной сложности алгоритмов». Они уже дают количественное определение сложности времени и пространства и, таким образом, выбирают два ресурса, которые по сей день считаются наиболее важными. При этом они выбирают многополосную машину Тьюринга в качестве основы и, таким образом, принимают очень надежное решение, применимое во многих областях теории сложности. Вы также уже работаете с первыми записями иерархии.

В тот же период времени, который включает около первых десяти лет исследований в области теории сложности, класс P формулируется как класс «практически решаемых» проблем. Алан Кобхэм показывает, что полиномиальное время устойчиво при выборе модели машины (которая сегодня суммируется в расширенном тезисе Черча-Тьюринга). Кроме того, многие математические функции оказываются вычислимыми за полиномиальное время.

Изучение класса NP

В 1979 году Майкл Р. Гэри и Дэвид С. Джонсон опубликовали книгу, описывающую 300 NP-полных проблем ( Компьютеры и неразрешимость ). Эта книга стала важным справочником для будущих исследователей.

Рандомизированные классы сложности

В этом обзоре были заложены важнейшие краеугольные камни истории теории сложности. Как и в других областях исследований, более свежие результаты разделены на множество, иногда очень специальных, подобластей.

Источник