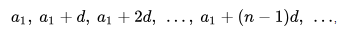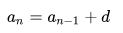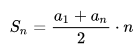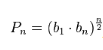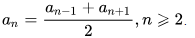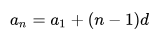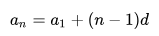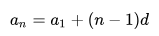Формула арифметической прогрессии что такое d

Арифметическая прогрессия: определение, формулы, свойства

Арифметическая прогрессия – это числовая последовательность, в которой, начиная со второго числа, каждое последующее равняется предыдущему плюс постоянное слагаемое.

Общий вид арифметической прогрессии

d – шаг или разность прогрессии; это и есть постоянное слагаемое.

Члены прогрессии:

Цифры 1,2,3… – это их порядковые номера, т.е. место, которое они занимают в последовательности.

Свойства и формулы арифметической прогрессии

1. Нахождение общего n-ого члена ( a_n )

2. Разность прогрессии

Также для нахождения шага используется такая формула:

3. Характеристическое свойство

Последовательность чисел a₁, a₂, a₃ … является арифметической прогрессией, если для любого ее члена выполняется следующее условие:

4. Сумма первых членов прогрессии

Чтобы найти сумму первых членов арифметической прогрессии, необходимо воспользоваться формулой:

5. Сумма членов прогрессии с n-ого по m-ный

6. Сходимость прогрессии

Источник

Алгебра. Урок 6. Прогрессии

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Числовые последовательности

Числовая последовательность – это функция, заданная на множестве натуральных чисел. Каждый элемент последовательности имеет свой порядковый номер.

Числа в последовательности могут быть любыми – положительными и отрицательными, целыми и дробными, рациональными и иррациональными.

Так почему же, спросите вы, в определении числовой последовательности есть фраза «функция, заданная на множестве натуральных чисел»? Потому что каждый член последовательности имеет свой порядковый номер (ну а нумеруем мы с единицы).

a 1 = 1, a 2 = 2, a 3 = 3, a 4 = 4, a 5 = 5, …

a 1 = 1, a 2 = 4, a 3 = 9, a 4 = 16, a 5 = 25, …

a 1 = − 3, a 2 = − 2, a 3 = − 1, a 4 = 0, a 5 = 1, a 6 = 2, a 7 = 3.

Числовые последовательности можно задавать несколькими способами:

Для нахождения каждого следующего члена последовательности требуется знать предыдущий.

n = 1, a n + 1 = a n + 1 ⇒ a 2 = a 1 + 1 = 1 + 1 = 2

n = 2, a n + 1 = a n + 1 ⇒ a 3 = a 2 + 1 = 2 + 1 = 3

n = 3, a n + 1 = a n + 1 ⇒ a 4 = a 3 + 1 = 3 + 1 = 4

n = 4, a n + 1 = a n + 1 ⇒ a 5 = a 4 + 1 = 4 + 1 = 5

Для нахождения каждого следующего члена последовательности требуется знать предыдущий.

n = 1, a n + 1 = ( a n + 1 ) 2 ⇒ a 2 = ( a 1 + 1 ) 2 = ( 1 + 1 ) 2 = 2 2 = 4

n = 2, a n + 1 = ( a n + 1 ) 2 ⇒ a 3 = ( a 2 + 1 ) 2 = ( 4 + 1 ) 2 = 3 2 = 9

n = 3, a n + 1 = ( a n + 1 ) 2 ⇒ a 4 = ( a 3 + 1 ) 2 = ( 9 + 1 ) 2 = 4 2 = 16

n = 4, a n + 1 = ( a n + 1 ) 2 ⇒ a 5 = ( a 4 + 1 ) 2 = ( 16 + 1 ) 2 = 5 2 = 25

a n + 1 = a n + 1 ⇒ a 2 = a 1 + 1 = − 3 + 1 = − 2 ; − 2 ≤ 3

a n + 1 = a n + 1 ⇒ a 3 = a 2 + 1 = − 2 + 1 = − 1 ; − 1 ≤ 3

a n + 1 = a n + 1 ⇒ a 4 = a 3 + 1 = − 1 + 1 = 0 ; 0 ≤ 3

a n + 1 = a n + 1 ⇒ a 5 = a 4 + 1 = 0 + 1 = 1 ; 1 ≤ 3

a n + 1 = a n + 1 ⇒ a 6 = a 5 + 1 = 1 + 1 = 2 ; 2 ≤ 3

a n + 1 = a n + 1 ⇒ a 7 = a 6 + 1 = 2 + 1 = 3 ; 3 ≤ 3

a n + 1 = a n + 1 ⇒ a 8 = a 7 + 1 = 3 + 1 = 4 ; 4 ≤ 3

Арифметическая прогрессия

Арифметической прогрессией < a n >называют числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом.

Разностью d арифметической прогрессии называют число, которое каждый раз прибавляют к предыдущему числу.

a 2 = a 1 + d a 3 = a 2 + d … a n = a n − 1 + d

Арифметическая прогрессия может быть

Примеры арифметической прогрессии:

Формулы арифметической прогрессии

(3) a n = a 1 + ( n − 1 ) d

Сумма n первых членов:

(4) S n = a 1 + a n 2 ⋅ n

(5) a n = a n − 1 + a n + 1 2

(6) a n = a n − k + a n + k 2

Геометрическая прогрессия

Геометрической прогрессией < b n >называют числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же данной последовательности число.

Знаменателем q геометрической прогрессии называют число, на которое каждый раз умножают предыдущее число.

Геометрическая прогрессия может быть

Примеры геометрической прогрессии:

Формулы геометрической прогрессии

(3) b n = b 1 ⋅ q n − 1

Сумма n первых членов:

(4) S n = b 1 ⋅ ( q n − 1 ) q − 1

(5) b n = b n − 1 ⋅ b n + 1

(6) b n = b n − k ⋅ b n + k

Задание №12 из ОГЭ 2020. Типовые задачи и принцип их решения.

Источник

Арифметическая прогрессия: что это такое?

Что ж, друзья, если вы читаете этот текст, то внутренний кэп-очевидность подсказывает мне, что вы пока ещё не знаете, что такое арифметическая прогрессия, но очень (нет, вот так: ОООООЧЕНЬ!) хотите узнать. Поэтому не буду мучать вас длинными вступлениями и сразу перейду к делу.

Для начала парочка примеров. Рассмотрим несколько наборов чисел:

Что общего у всех этих наборов? На первый взгляд — ничего. Но на самом деле кое-что есть. А именно: каждый следующий элемент отличается от предыдущего на одно и то же число.

Так вот: все такие последовательности как раз и называются арифметическими прогрессиями. Дадим строгое определение:

И сразу парочка важных замечаний. Во-первых, прогрессией считается лишь упорядоченная последовательность чисел: их разрешено читать строго в том порядке, в котором они записаны — и никак иначе. Переставлять и менять местами числа нельзя.

Ладно, ладно: последний пример может показаться чересчур сложным. Но остальные, думаю, вам понятны. Поэтому введём новые определения:

Определение. Арифметическая прогрессия называется:

Как видим, во всех трёх случаях разность действительно получилась отрицательной. И теперь, когда мы более-менее разобрались с определениями, пора разобраться с тем, как описываются прогрессии и какие у них свойства.

Члены прогрессии и рекуррентная формула

Поскольку элементы наших последовательностей нельзя менять местами, их можно пронумеровать:

Отдельные элементы этого набора называются членами прогрессии. На них так и указывают с помощью номера: первый член, второй член и т.д.

Кроме того, как мы уже знаем, соседние члены прогрессии связаны формулой:

Наверняка вы уже встречались с этой формулой. Её любят давать во всяких справочниках и решебниках. Да и в любом толковом учебнике по математике она идёт одной из первых.

Тем не менее предлагаю немного потренироваться.

Вот и всё! Обратите внимание: наша прогрессия — убывающая.

Задача №2. Выпишите первые три члена арифметической прогрессии, если её седьмой член равен −40, а семнадцатый член равен −50.

Решение. Запишем условие задачи в привычных терминах:

Знак системы я поставил потому, что эти требования должны выполняться одновременно. А теперь заметим, если вычесть из второго уравнения первое (мы имеем право это сделать, т.к. у нас система), то получим вот что:

Вот так просто мы нашли разность прогрессии! Осталось подставить найденное число в любое из уравнений системы. Например, в первое:

Теперь, зная первый член и разность, осталось найти второй и третий член:

Готово! Задача решена.

Простое, но очень полезное свойство, которое обязательно надо знать — с его помощью можно значительно ускорить решение многих задач по прогрессиям. Вот яркий тому пример:

Задача №3. Пятый член арифметической прогрессии равен 8,4, а её десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.

Вот и всё! Нам не потребовалось составлять какие-то системы уравнений и считать первый член и разность — всё решилось буквально в пару строчек.

Теперь рассмотрим другой вид задач — на поиск отрицательных и положительных членов прогрессии. Не секрет, что если прогрессия возрастает, при этом первый член у неё отрицательный, то рано или поздно в ней появятся положительные члены. И напротив: члены убывающей прогрессии рано или поздно станут отрицательными.

При этом далеко не всегда можно нащупать этот момент «в лоб», последовательно перебирая элементы. Зачастую задачи составлены так, что без знания формул вычисления заняли бы несколько листов — мы просто уснули бы, пока нашли ответ. Поэтому попробуем решить эти задачи более быстрым способом.

Задача №4. Сколько отрицательных членов в арифметической прогрессии −38,5; −35,8; …?

Заметим, что разность положительна, поэтому прогрессия возрастает. Первый член отрицателен, поэтому действительно в какой-то момент мы наткнёмся на положительные числа. Вопрос лишь в том, когда это произойдёт.

Кроме того, попробуем выразить пятый член через первый и разность по стандартной формуле:

Теперь поступаем по аналогии с предыдущей задачей. Выясняем, в какой момент в нашей последовательности возникнут положительные числа:

Минимальное целочисленное решение данного неравенства — число 56.

Теперь, когда мы научились решать простые задачи, перейдём к более сложным. Но для начала давайте изучим ещё одно очень полезное свойство арифметических прогрессий, которое в будущем сэкономит нам кучу времени и неравных клеток.:)

Среднее арифметическое и равные отступы

Члены арифметической прогрессии на числовой прямой

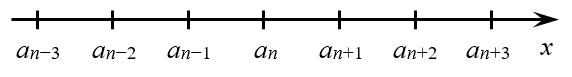
А правило очень простое. Давайте вспомним рекуррентную формулу и запишем её для всех отмеченных членов:

Однако эти равенства можно переписать иначе:

Члены прогрессии лежат на одинаковом расстоянии от центра

Решение. Опять выразим средний член через среднее арифметическое соседних членов:

Если в процессе решения задачи у вас вылезают какие-то зверские числа, либо вы не до конца уверены в правильности найденных ответов, то есть замечательный приём, позволяющий проверить: правильно ли мы решили задачу?

Опять прогрессия, но с разностью 27. Таким образом, задача решена верно. Желающие могут проверить вторую задачу самостоятельно, но сразу скажу: там тоже всё верно.

В целом, решая последние задачи, мы наткнулись на ещё один интересный факт, который тоже необходимо запомнить:

Если три числа таковы, что второе является средним арифметическим первого и последнего, то эти числа образуют арифметическую прогрессию.

В будущем понимание этого утверждения позволит нам буквально «конструировать» нужные прогрессии, опираясь на условие задачи. Но прежде чем мы займёмся подобным «конструированием», следует обратить внимание на ещё один факт, который прямо следует из уже рассмотренного.

Группировка и сумма элементов

Давайте ещё раз вернёмся к числовой оси. Отметим там несколько членов прогрессии, между которыми, возможно. стоит очень много других членов:

На числовой прямой отмечены 6 элементов

А теперь заметим, что равны следующие суммы:

Одинаковые отступы дают равные суммы

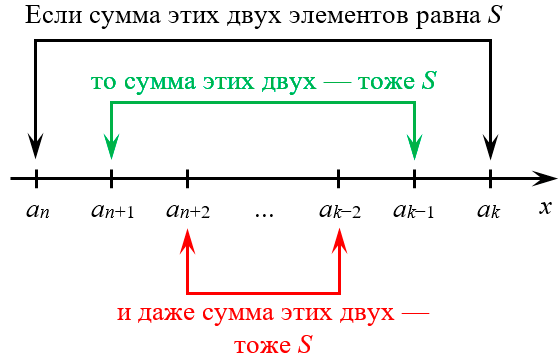
Понимание данного факта позволит нам решать задачи принципиально более высокого уровня сложности, нежели те, что мы рассматривали выше. Например, такие:

Задача №8. Определите разность арифметической прогрессии, в которой первый член равен 66, а произведение второго и двенадцатого членов является наименьшим из возможных.

Решение. Запишем всё, что нам известно:

\[\begin & f\left( d \right)=11\left( <^<2>>+66d+6d+66\cdot 6 \right)= \\ & =11<^<2>>+11\cdot 72d+11\cdot 66\cdot 6 \end\]

Как видим, коэффициент при старшем слагаемом равен 11 — это положительное число, поэтому действительно имеем дело с параболой ветвями вверх:

график квадратичной функции — парабола

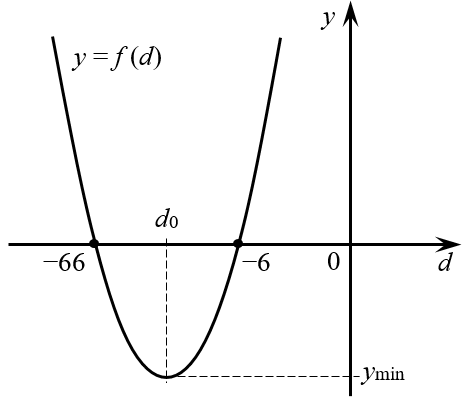
Именно поэтому я не особо спешил раскрывать скобки: в исходном виде корни было найти очень и очень просто. Следовательно, абсцисса равна среднему арифметическому чисел −66 и −6:

Аналогично рассуждая, находим оставшееся число:

Готово! Мы нашли все три числа. Запишем их в ответе в том порядке, в котором они должны быть вставлены между исходными числами.

Задача №10. Между числами 2 и 42 вставьте несколько чисел, которые вместе с данными числами образуют арифметическую прогрессию, если известно, что сумма первого, второго и последнего из вставленных чисел равна 56.

Далее распишем сумму первого, второго и последнего из вставленных чисел:

Но тогда записанное выше выражение можно переписать так:

Осталось лишь найти остальные члены:

Таким образом, уже на 9-м шаге мы придём в левый конец последовательности — число 42. Итого нужно было вставить лишь 7 чисел: 7; 12; 17; 22; 27; 32; 37.

Ответ: 7; 12; 17; 22; 27; 32; 37

Текстовые задачи с прогрессиями

В заключение хотелось бы рассмотреть парочку относительно простых задач. Ну, как простых: для большинства учеников, которые изучают математику в школе и не читали того, что написано выше, эти задачи могут показаться жестью. Тем не менее именно такие задачи попадаются в ОГЭ и ЕГЭ по математике, поэтому рекомендую ознакомиться с ними.

Задача №11. Бригада изготовила в январе 62 детали, а в каждый следующий месяц изготовляла на 14 деталей больше, чем в предыдущий. Сколько деталей изготовила бригада в ноябре?

Решение. Очевидно, количество деталей, расписанное по месяцам, будет представлять собой возрастающую арифметическую прогрессию. Причём:

Следовательно, в ноябре будет изготовлено 202 детали.

Задача №12. Переплётная мастерская переплела в январе 216 книг, а в каждый следующий месяц она переплетала на 4 книги больше, чем в предыдущий. Сколько книг переплела мастерская в декабре?

Решение. Всё то же самое:

Это и есть ответ — 260 книг будет переплетено в декабре.

Что ж, если вы дочитали до сюда, спешу вас поздравить: «курс молодого бойца» по арифметическим прогрессиям вы успешно прошли. Можно смело переходить к следующему уроку, где мы изучим формулу суммы прогрессии, а также важные и очень полезные следствия из неё.

Источник

Арифметическая прогрессия

п.1. Понятие арифметической прогрессии

п.2. Формула n-го члена арифметической прогрессии

По определению арифметической прогрессии мы получаем рекуррентную формулу для n-го члена: a_n = a_n-1 + d. Из неё можно вывести аналитическую формулу:

Например:
Найдём a₇, если известно, что a₁ = 5, d = 3.
По формуле n-го члена получаем: a₇ = a₁ + 6d = 5 + 6 · 3 = 23

п.3. Свойства арифметической прогрессии

Свойство 1. Линейность

Арифметическая прогрессия является линейной функцией f(n) = kn + b:

с угловым коэффициентом k = d и свободным членом b = a₁ – d.

Свойство 2. Признак арифметической прогрессии

Например:
Найдём a₉, если известно, что a₇ = 10, a₁₁ = 15
По следствию из признака арифметической прогрессии: \(\mathrm><2>=\frac<10+15><2>=12,5>\)

Свойство 3. Равенство сумм индексов

Например:
Найдём a₆, если известно, что a₂ = 5, a₄ = 10, a₈ = 20
По равенству сумм индексов a₂ + a₈ = a₄ + a₆
Откуда a₆ = a₂ + a₈ – a₄ = 5 + 20 – 10 = 15

п.4. Сумма первых n членов арифметической прогрессии

Например:
Найдём сумму первых 100 натуральных чисел: 1 + 2 +. + 100
В этом случае a₁ = 1, a₁₀₀ = 100, n = 100
\(\mathrm< S_<100>=\frac<1+100><2>\cdot 100=5050>\)

п.5. Примеры

Пример 1. Найдите первый член и разность арифметической прогрессии, если:
а) a₇ = 10, a₁₅ = 42
Найдем разность данных членов: a₁₅ – a₇ = (a₁ + 14d) – (a₁ + 6d) = 8d
Получаем разность прогрессии: 42 – 10 = 8d ⇒ d = 32 : 8 = 4
7-й член: a₇ = a₁ + 6d = a₁ + 6 · 4 = 10 ⇒ a₁ = 10 – 24 = –14
Ответ: a₁ = –14, d = 4

б) a₁₀ = 95, S₁₀ = 500
Сумма прогрессии: \(\mathrm=\frac><2>\cdot 10\Rightarrow 500=(a_1+95)\cdot 5\Rightarrow a_1+95=100\Rightarrow a_1=5>\)
10-й член: \(\mathrm=a_1+9d\Rightarrow95=5+9d\Rightarrow 9d=90\Rightarrow d=10>\)
Ответ: a₁ = 5, d = 10

Пример 2. Найдите сумму первых 100 нечётных натуральных чисел.
Чему равно последнее слагаемое этой суммы?
Ищем сумму \(\mathrm<\underbrace<1+3+5+. >_<100\ \text<слагаемых>>>\)
По условию a₁ = 1, d = 2, n = 100. Получаем:
\(\mathrm=\frac<2a_1+d(n-1)><2>n=\frac<2\cdot 1+2\cdot 99><2>\cdot 100=10000>\)
Формула n-го члена данной прогрессии: \(\mathrm\)
100-й член \(\mathrm=2\cdot 100-1=199>\)
Ответ: S₁₀₀ = 10000, a₁₀₀ = 199

n = m – k + 1 = 56 – 18 + 1 = 39

Пример 4. Одиннадцатый член арифметической прогрессии равен 7.
Найдите сумму её первых 21 членов.
По свойству суммы индексов: a₁₁ + a₁₁ = a₁ + a₂₁
Откуда a₁ + a₂₁ = 2a₁₁ = 14
Искомая сумма: \(\mathrm=\frac><2>\cdot 21=\frac<14><2>\cdot 21=147>\)
Ответ: 147

Пример 6. При каких значениях x числа x 2 – 11, 2x 2 + 29, x 4 – 139 в заданной последовательности являются членами арифметической прогрессии?
Для последовательных членов получаем уравнение:

a₂ – a₁ = a₃ – a₂
(2x 2 + 29) – (x 2 – 11) = (x 4 – 139) – (2x 2 + 29)
x 4 – 3x 2 – 208 = 0 ⇒ (x 2 + 13)(x 2 – 16) = 0 ⇒ x 2 = 16 ⇒ x = ±4

Пример 7. Сумма первых трёх членов убывающей арифметической прогрессии равна 9, а сумма их квадратов равна 99. Найдите седьмой член прогрессии.
По условию d 3a₂ = 9 ⇒ a_2 = 3

Тогда a₁ = a₂ – d = 3 – d, a₃ = a₂ + d = 3 + d. Подставляем во второе уравнение:

(3 – d) 2 + 3 2 + (3 + d) 2 = 99
9 – 6d + d 2 + 9 + 9 + 6d + d 2 = 99
2d 2 = 72 ⇒ d 2 = 36 ⇒ d = ±6

Выбираем отрицательное значение d = –6
1-й член прогрессии: a₁ = a₂ – d = 3 + 6 = 9
7-й член прогрессии: a₇ = a₁ + 6d = 9 + 6(–6) = –27
Ответ: x = –27

Источник

Арифметическая (алгебраическая) прогрессия определение, примеры нахождения с решением

Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией.

Одна из главных отличительных особенностей такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций.

Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др.

Онлайн-калькулятор арифметической прогрессии

Определение и примеры арифметической прогрессии

Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.

Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности.

Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.

Кроме этого, существуют виды таких рядов:

В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.

Виды арифметической (алгебраической) прогрессии

Разновидности строятся на основании характеристики разности (d), а именно на основании отличия последней от нуля.

Таким образом, можно встретить определенные вариации:

Если прогрессия не изменяется с каждым шагом на одну и ту же разность, то эта прогрессия непостоянная и арифметической не является.

Важно знать: арифметическая от геометрической отличается тем, что в последней производится увеличение каждого последующего на один и тот же множитель.

Формулы арифметической прогрессии

Одно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда.

Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (an-1), к которому прибавляют разность (d):

Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки.

Итак, нам понадобится значение первого числа в ряду (a1) и последнего (an), а также информация об общем количестве чисел в ряду. Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом:

Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы.

Произведение членов арифметической прогрессии можно находить по похожей формуле:

где, Pn – произведение, b1 и bn – соответственно первое и последнее числа, а n – количество членов.

Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента:

Примеры задач с решением

Рассмотрим как решать задачи на заданную тему.

Пример 1

Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…».

Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a1) и о разности (d). Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – и получаем d = 7. Теперь мы можем считать по формуле:

Подставляя полученные значения, получим выражение вида a574 = 8 + (574-1) * 7.

После вычисления получаем ответ: a574 = 4019.

Пример 2

Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8.

Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера:

Подставляя известные значения, получаем выражение – а544 = 17 + (544 1) * 8.

Вычисляя, получаем ответ а544 = 4361.

Пример 3

Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов.

Требуется выяснить, сколько времени у студента ушло на подготовку.

Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных:

После подстановки получаем выражение: 730 = 17 + (n 1) * 27.

После вычислений определяем ответ – 27 дней.

Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется.

Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм.

Источник