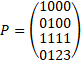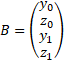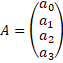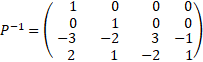Формула эрмита для чего
ЭРМИТА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА
Э. и. ф. может быть записана в виде:
где
Лит.:[1] Березин И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966.
М. К. Самарин.
Смотреть что такое «ЭРМИТА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА» в других словарях:
КВАДРАТУРНАЯ ФОРМУЛА — приближенная формула для вычисления определенного интеграла: в левой части стоит интеграл, подлежащий вычислению. Подинтегральная функция записана в виде произведения двух функций. Первая из них р(х)считается фиксированной для данной К. ф. и наз … Математическая энциклопедия
ИНТЕРПОЛИРОВАНИЕ — интерполяция, в простейшем, классическом смысле конструктивное восстановление (быть может, приближенное) функции определенного класса по известным ее значениям или значениям ее производных в данных точках. Пусть даны n+l точек сегмента D=[ а, b] … Математическая энциклопедия
Разделённая разность — Разделённая разность обобщение понятия производной для дискретного набора точек. Содержание 1 Определение 2 Применение 3 История … Википедия
ЭРМИТА ФУНКЦИИ
Частные решения (1) имеют вид
При целом v>0 Э. ф. совпадают с полиномами Эрмита (см. Ортогональные полиномы). Интегральное представление, ф-лу дифференцирования и рекуррентное соотношение для Э. v (z )см. в ст. Параболического цилиндра функции. Э. ф. можно выразить через вырожденные гипергеометрические функции:
Используя свойства гипергеометрических ф-ций, получим разложение в ряд
Асимптотич. представление при
Для ф-ций H v (z )имеют место функциональные соотношения
Полезное
Смотреть что такое «ЭРМИТА ФУНКЦИИ» в других словарях:
ЭРМИТА ФУНКЦИИ — решения Эрмита уравнения Э. ф. имеют вид где C1 контур в комплексной плоскости t, состоящий из лучей и полуокружности |t|=а>0, С 2= С1. Полусумма этих решений при целом равна Эрмита многочлену Hn(z). Уравнением Эрмита наз. также уравнение … Математическая энциклопедия
Функции параболического цилиндра — (функции Вебера) общее название для специальных функций, являющихся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, таких как уравнение Лапласа, уравнение… … Википедия
Функции Эрмита — Функции параболического цилиндра общее название для специальных функций, являющихся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, таких как уравнение Лапласа,… … Википедия
ЭРМИТА УРАВНЕНИЕ — линейное однородное обыкновенное дифференциальное уравнение 2 го порядка или, в самосопряженной форме, здесь константа. Замена неизвестной функции приводит Э. у. к уравнению а после замены переменных из Э. у. получается Вебера уравнение Э. у. при … Математическая энциклопедия
ЭРМИТА МНОГОЧЛЕНЫ — многочлены Чебышева Эрмита, многочлены, ортогональные на интервале с весовой функцией k(x)=ехр( х 2). Стандартизованные Э. м. определяются Родрига формулой Наиболее употребительны формулы Первые Э. м. имеют вид Многочлен Hn (х)удовлетворяет… … Математическая энциклопедия
ПАРАБОЛИЧЕСКОГО ЦИЛИНДРА ФУНКЦИИ — Вебера функции, Вебера Эрмита функции, решения дифференциального уравнения к рое получается в результате разделения переменных в волновом уравнении в параболических ци линдрич. координатах. Наиболее часто используется решение где вырожденная… … Математическая энциклопедия
Многочлены Эрмита — Многочлены Эрмита определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1… … Википедия
Функция Эрмита — Функции параболического цилиндра общее название для специальных функций, являющихся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, таких как уравнение Лапласа,… … Википедия
Сплайн Эрмита — Кубический эрмитов сплайн сплайн, построенный из кубических полиномов с использованием эрмитовой интерполяции, в соответствии с которой интерполируемая функция задается не только своими значениями в n точках, но и ее первыми производными. Для… … Википедия
Интерполяционный многочлен Эрмита
Общая информация
Интерполирование по Эрмиту есть специальный вид многоинтервальной интерполяции, при котором интерполирующий многочлен Hn(х) обеспечивает не только равенство Hn(х) значениям f(x), но и совпадение некоторого количества производных в узлах интерполяции.
Многочлен Эрмита единственный, это следует из однозначности его построения.
Остаточный член интерполяционной формулы Эрмита равен:
Rn(x)=f(x)-Hn(x)=f (n+1) (ξ)*(x-x0) N0 *. *(x-xm) Nm /(n+1)!, где ξ∈[x0,xm]
Алгоритм построения
Правая часть системы линейных уравнений, это столбец с координатами y0,z0,y1,z1
Вектор-столбец неизвестных переменных обозначим
Тогда нам нужно решить систему линейных уравнений P*A=B
Воспользуемся алгоритмом Гаусса:
для этого в левой части таблицы запишем матрицу P, a справа приписывается единичная матрица
Задача привести матрицу некоторыми преобразованиями к такому виду, чтобы слева оказалась единичная матрица, а то что будет в правой половине и будет обратной матрицей
По значениям в концах отрезка [0,1] и их производных, мы восстановили всю функцию
Пусть нужно произвести интерполяцию на отрезке [x0;x1 ], тогда график функции необходимо сдвинуть на x0 и растянуть в x1-x0 раз, а поскольку z0,z1 в x1-x0 раз меньше, чем требуется, то их необходимо домножить.
Для удобства введем k=(x-x0)/(x1-x0) и h=x1-x0. Функция примет вид:
Аналогичным образом определяется многочлен любой степени.
При добавлении значений производных (до некоторого порядка m) в точках добавляются дополнительные слагаемые.
Точность растет с увеличением количества известных значений производных в точках.
Полиномы Эрмита
Многочлены Эрмита — определенного вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике.
Содержание
Определение
В теории вероятностей полиномы Эрмита обычно определяются выражением:
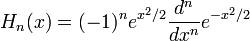
в физике обычно используется другое определение:
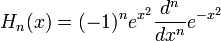
Два определения, приведенные выше, не являются в точности эквивалентными друг другу; каждое из них является «отмасштабированной» версией другого
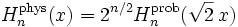
Явные выражения для первых десяти многочленов Эрмита приведены ниже (вероятностное определение):
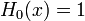
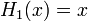
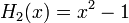
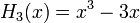
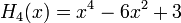
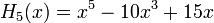
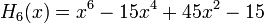
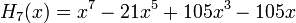
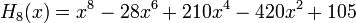
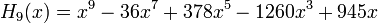
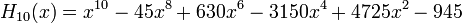
Свойства
Ортогональность
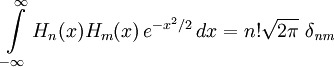
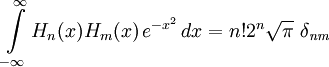
Таким образом, многочлены Эрмита образуют отрогональный базис в Гильбертовом пространстве функций, ограниченных в соответствующей норме
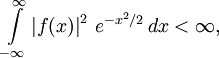
Дифференциальное уравнение Эрмита
Многочлен Эрмита n-го порядка удовлетворяет дифференциальному уравнению Эрмита:
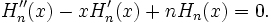
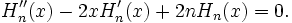
Рекурсивное выражение
Последовательность многочленов Эрмита допускает рекурсивное определение:
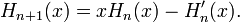
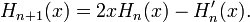
Применение
Ссылки
Полезное
Смотреть что такое «Полиномы Эрмита» в других словарях:
ЭРМИТА ФУНКЦИИ — специальные функции, удовлетворяющие ур нию Эрмита (С. Hermit) Частные решения (1) имеют вид При целом v>0 Э. ф. совпадают с полиномами Эрмита (см. Ортогональные полиномы). Интегральное представление, ф лу дифференцирования и рекуррентное… … Физическая энциклопедия
Полиномы — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия
Многочлен Эрмита — Многочлены Эрмита определенного вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1 Определение 2 … Википедия
Полином Эрмита — Многочлены Эрмита определенного вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1 Определение 2 … Википедия
Многочлены Эрмита — Многочлены Эрмита определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1… … Википедия
Сплайн Эрмита — Кубический эрмитов сплайн сплайн, построенный из кубических полиномов с использованием эрмитовой интерполяции, в соответствии с которой интерполируемая функция задается не только своими значениями в n точках, но и ее первыми производными. Для… … Википедия
ПРИБЛИЖЕНИЕ ФУНКЦИЙ — замена по определенному правилу функции f(t).близкой к ней в том или ином смысле функцией j(t). из заранее фиксированного множества (приближающего множества). Предполагается, что функция f определена на том множестве Qm мерного евклидова… … Математическая энциклопедия
Эрмит, Шарль — Шарль Эрмит Шарль Эрмит (190 … Википедия
Шарль Эрмит — (фр. Charles Hermite; 24 декабря 1822, Дьёзе, Лотарингия, Франция 14 января 1901, Париж, Франция) французский математик. Основные работы в теории чисел, теории квадратичных форм, теории инвариантов, ортогональных многочленов, эллиптических… … Википедия
Эрмиталь ® (Ermytal) инструкция по применению
Владелец регистрационного удостоверения:
Произведено:
Выпускающий контроль качества:
Контакты для обращений:
Лекарственные формы
Форма выпуска, упаковка и состав препарата Эрмиталь ®
| 1 капс. | |
| панкреатин | 87.28-112.96 мг |
| с ферментативной активностью: | |
| липазы | 10000 ЕД |
| амилазы | 9000 ЕД |
| протеаз | 500 ЕД |
Вспомогательные вещества: целлюлоза микрокристаллическая, кросповидон, кремния диоксид коллоидный безводный, магния стеарат.
Состав крышечки капсулы: желатин, оксид железа красный (Е172), оксид железа черный (Е172), титана диоксид (Е171), лаурилсульфат натрия.
Состав корпуса капсулы: желатин, лаурилсульфат натрия.
| 1 капс. | |
| панкреатин | 218.2-282.4 мг |
| с ферментативной активностью: | |
| липазы | 25000 ЕД |
| амилазы | 22500 ЕД |
| протеаз | 1 250 ЕД |
Вспомогательные вещества: целлюлоза микрокристаллическая, кросповидон, кремния диоксид коллоидный безводный, магния стеарат.
Состав крышечки капсулы: желатин, оксид железа красный (Е172), оксид железа черный (Е172), титана диоксид (Е171), лаурилсульфат натрия.
Состав корпуса капсулы: желатин, лаурилсульфат натрия.
| 1 капс. | |
| панкреатин | 272.02-316.68 мг |
| с ферментативной активностью: | |
| липазы | 36000 ЕД |
| амилазы | 18000 ЕД |
| протеаз | 1200 ЕД |
Вспомогательные вещества: целлюлоза микрокристаллическая, кросповидон, кремния диоксид коллоидный безводный, магния стеарат.
Состав крышечки капсулы: желатин, оксид железа красный (Е172), оксид железа черный (Е172), титана диоксид (Е171), лаурилсульфат натрия.
Состав корпуса капсулы: желатин, лаурилсульфат натрия.
× флакон снабжен уплотнительным диском, состоящим из двух частей, скрепленных восковыми точками.
Фармакологическое действие
Фармакокинетика
Форма выпуска препарата обеспечивает полное высвобождение резистентных к действию желудочного сока микротаблеток из капсулы в желудке с последующим мелкодисперсным перемешиванием микротаблеток с кишечным содержимым и химусом и быстрым выделением ферментов из микротаблеток в двенадцатиперстной кишке.
Ферменты поджелудочной железы не всасываются в кровь. Ферменты инактивируются и перевариваются в кишечнике, как белки путем аутолиза и протеолиза.
Показания препарата Эрмиталь ®
У взрослых и детей:
Открыть список кодов МКБ-10
| Код МКБ-10 | Показание |
| C25 | Злокачественное новообразование поджелудочной железы |
| E84 | Кистозный фиброз |
| K30 | Функциональная диспепсия (нарушение пищеварения) |
| K50 | Болезнь Крона [регионарный энтерит] |
| K63.8 | Другие уточненные болезни кишечника |
| K73 | Хронический гепатит, не классифицированный в других рубриках |
| K74 | Фиброз и цирроз печени |
| K83.1 | Закупорка желчного протока |
| K86.1 | Другие хронические панкреатиты |
| K86.8 | Другие уточненные болезни поджелудочной железы (атрофия, камни, цирроз, фиброз поджелудочной железы) |
| K90.3 | Панкреатическая стеаторея |
| K91.1 | Синдромы оперированного желудка |
| K91.2 | Нарушение всасывания после хирургических вмешательств, не классифицированное в других рубриках |
| K91.5 | Постхолецистэктомический синдром |
| K91.8 | Другие нарушения органов пищеварения после медицинских процедур, не классифицированные в других рубриках |
| Y83.6 | Удаление другого органа (частичное) (полное) |
| Z72.4 | Неприемлемый пищевой рацион и вредные привычки в приеме пищи |
Режим дозирования
Внутрь, дозы подбирают индивидуально в зависимости от тяжести заболевания и диеты.
Расчет дозы проводится в перерасчете на единицы активности липазы.
Доза зависит от массы тела и должна составлять в начале лечения 1000 липазных единиц/кг на каждый прием пищи для детей младше 4 лет и 500 липазных единиц/кг во время приема пищи для детей старше 4 лет и взрослых.
Дозу следует определять в зависимости от выраженности симптомов заболевания, результатов контроля за стеатореей и поддержания адекватного нутритивного статуса. У большинства пациентов доза должна оставаться меньше или не превышать 10 000 липазных единиц/кг массы тела в сутки или 4000 липазных единиц/г потребленного жира.
Другие состояния, сопровождающиеся экзокринной недостаточностью поджелудочной железы
Рекомендуемая доза составляет 2-4 капс. препарата Эрмиталь ® 10000 ЕД, или 1-2 капс. препарата Эрмиталь ® 25000 ЕД, или 1 капс. препарата Эрмиталь ® 36000 ЕД во время каждого приема пищи. При необходимости доза может быть увеличена. Повышение дозы должно проходить под контролем врача. Нельзя превышать суточную дозу ферментов в пределах 15-20 тыс. липазных единиц на кг массы тела. Терапия должна проводиться на фоне обильного приема жидкости.
У детей препарат должен применяться в соответствии с назначением врача.
Побочное действие
Аллергические реакции наблюдались преимущественно со стороны кожных покровов, но отмечались также и другие проявления аллергии. Сообщения о данных побочных эффектах были получены в период постмаркетингового применения и носили спонтанный характер. Для точной оценки частоты случаев имеющихся данных недостаточно.
При применении у детей не было отмечено каких-либо специфических нежелательных реакций. Частота, тип и степень тяжести нежелательных реакций у детей с муковисцидозом были сходны с таковыми у взрослых.
Противопоказания к применению
Применение при беременности и кормлении грудью
Применение препарата Эрмиталь ® при беременности и в период лактации возможно только после тщательной оценки соотношения пользы для матери и риска для плода или младенца. В связи с незначительной системной абсорбцией панкреатина, негативного влияния на организм матери, а также плода и младенца, не ожидается.
Применение у детей
У детей препарат должен применяться в соответствии с назначением врача.
Особые указания
При длительном применении панкреатина в высоких дозах у пациентов с муковисцидозом возможно развитие запоров, стриктур подвздошной и слепой кишки (фиброзирующая колонопатия), колит.
При приеме препарата в высоких дозах (более 10000 липазных единиц/кг массы тела в сутки) следует тщательно контролировать необычные симптомы и побочные эффекты со стороны органов ЖКТ и, при необходимости, проводить медицинское обследование для исключения фиброзирующей колонопатии.
Препарат Эрмиталь ® содержит активные ферменты, которые при высвобождении в полости рта (например, при жевании) могут вызвать раздражение и изъязвление слизистой оболочки. Поэтому микротаблетки следует глотать, не разжевывая.
Влияние на способность управлять транспортными средствами, механизмами
Препарат не влияет на способность управлять транспортными средствами, механизмами.
Передозировка
При приеме панкреатина в высоких дозах возможно развитие гиперурикозурии и гиперурикемии, особенно у пациентов с муковисцидозом.
Лечение: отмена препарата, симптоматическая терапия.
Лекарственное взаимодействие
При приеме препарата Эрмиталь ® может снижаться всасывание фолиевой кислоты.
На фоне лечения препаратом Эрмиталь ® может снижаться эффект пероральных гипогликемических лекарственных средств акарбозы и миглитола.
Условия хранения препарата Эрмиталь ®
Препарат следует хранить в недоступном для детей месте при температуре не выше 25°C.