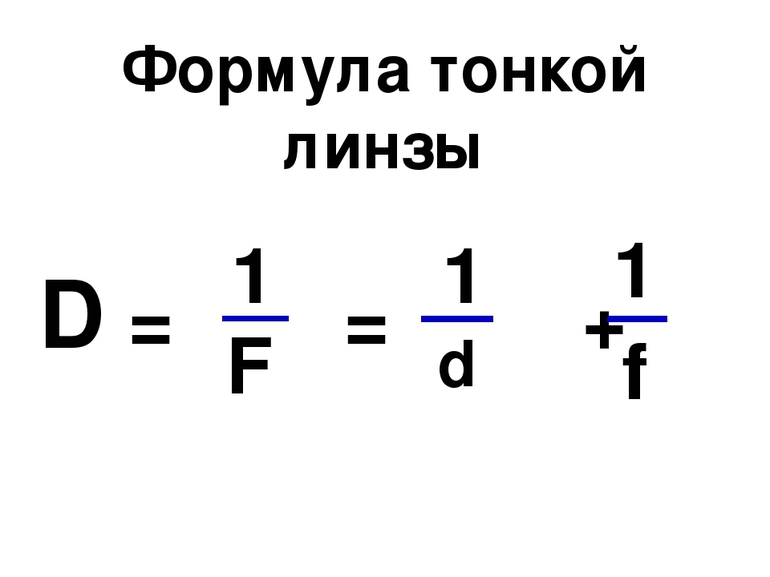
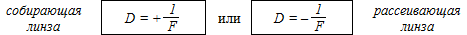Формула тонкой линзы в чем измеряется

Тонкие линзы

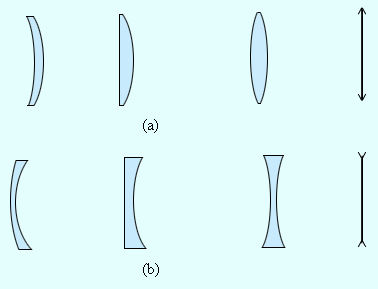
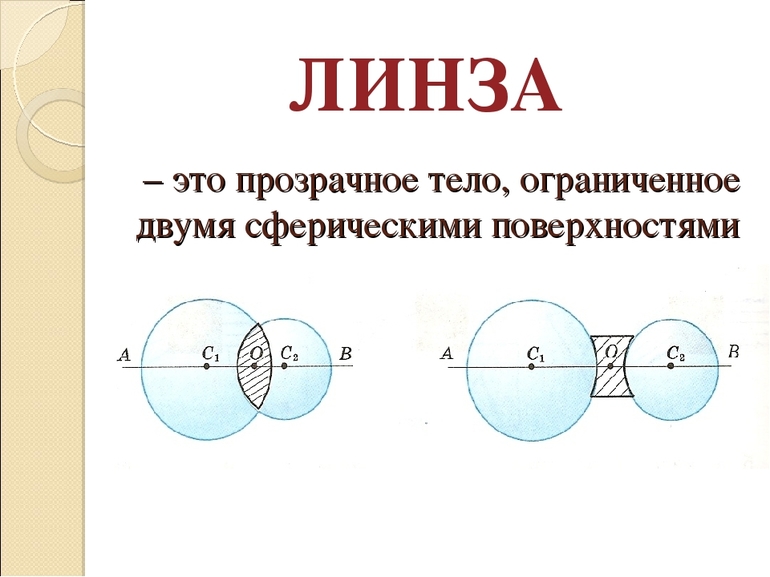
Линза – это прозрачное тело, имеющая 2 сферические поверхности. Она, является тонкой, если ее толщина меньше радиусов кривизны сферических поверхностей.

Линза, имеющая большую толщину по краям, называется рассеивающей.

Главная оптическая ось – это прямая, которая проходит через центры кривизны O 1 и O 2 сферических поверхностей.

Побочные оптические оси – это прямые, проходящие через оптический центр.

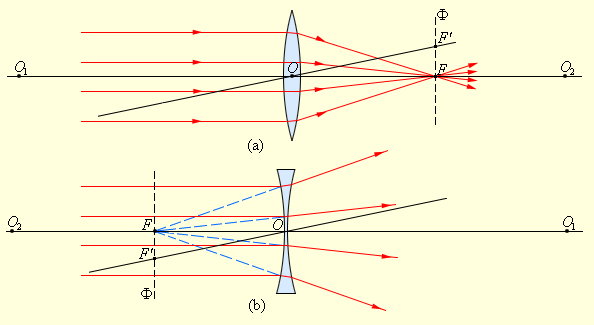
Эта точка получила название главный фокус линзы.

Тонкая линза имеет два главных фокуса, которые располагаются симметрично на главной оптической оси по отношению к линзе.

Фокус собирающей линзы – действительный, а у рассеивающей – мнимый.

Главным свойством линз является способность передавать изображения предметов. Они, в свою очередь, бывают:

Построение изображения в линзах

Величина D – это оптическая сила линзы, равная обратному фокусному расстоянию.

Величина d и f тоже подчиняются определенным знакам:

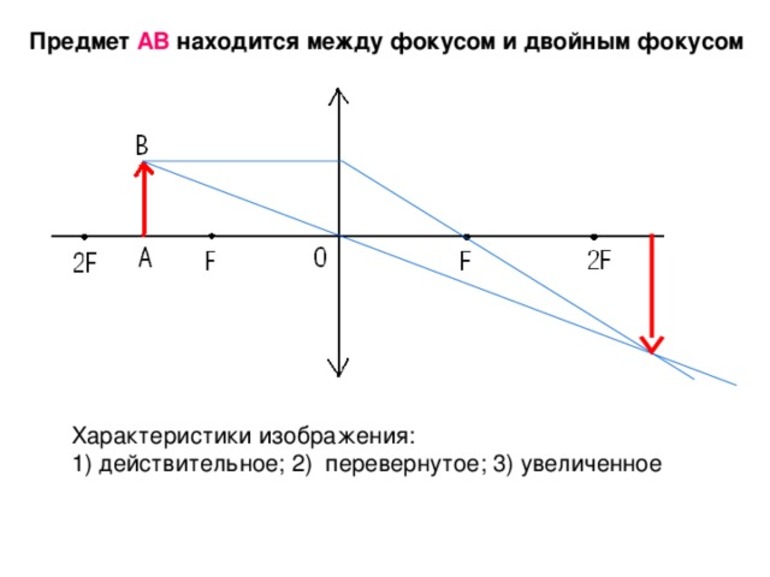
Линейные размеры изображения зависят от положения предмета по отношению к линзе.

Выпуклая поверхность имеет положительный радиус кривизны, а вогнутая поверхность – отрицательным. Данная формула применима в изготовлении линз с заданной оптической силой.

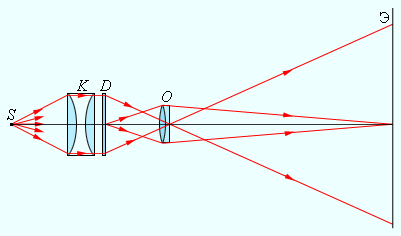
Астрономическая труба Кеплера и земная труба Галилея

Тонкая линза имеет некоторые недостатки, которые не позволяют получать изображения высокого разрешения.

Аберрация – это искажение, которое возникает в процессе формирования изображения. В зависимости от расстояния, на котором проводится наблюдение, аберрации могут быть сферическими и хроматическими.

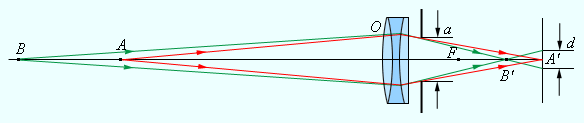
Смысл сферической аберрации в том, что при широких световых пучках лучи, находящиеся на далеком расстоянии от оптической оси, пересекают ее не в месте фокуса. Формула тонкой линзы действует лишь для лучей, которые находятся близко к оптической оси. Изображение удаленного источника, которое создается широким пучком лучей, преломленных линзой, размыто.

Современные оптические приборы оснащены не тонкими линзами, а сложными линзовыми системами, в которых есть возможность исключить некоторые искажения.

В таких приборах, как фотоаппараты, проекторы и т.д., используются собирающие линзы для формирования действительных изображений предметов.

Что представляет собой фотоаппарат

Фотоаппарат – это замкнутая светонепроницаемая камера, в которой изображение запечатленных предметов создается на пленке системой линз – объективом. На время экспозиции объектив открывается и закрывается с помощью специального затвора.

Источник

Общие сведения

Согласно физическому определению, под линзой понимают оптическую систему, которая состоит из прозрачного для электромагнитных волн вещества, и которая ограничена хотя бы одной кривой поверхностью (вторая может быть плоской). Прозрачное вещество должно обладать способностью преломлять свет, что возможно, если оно имеет отличный от окружающей среды коэффициент преломления. Оптический объект будет только тогда обладать всеми своими свойствами, если коэффициент преломления вещества, из которого он изготовлен, будет больше этого показателя для окружающей среды.

Слово «линза» произошло от латинского lentis, которое означает «чечевица». Такое название связано с похожестью формы оптического объекта и плода растения.

Линзы используются человеком издревле для разных хозяйственных нужд. Так, в своей работе «Облака» (423 год до нашей эры) греческий философ Аристофан упоминает об их применении в качестве предмета для размягчения воска с помощью фокусировки солнечных лучей. Начиная с XV века, в Европе возникает индустрия производства оптики. С этого времени развивается теоретическая база для ее использования.

Виды и типы

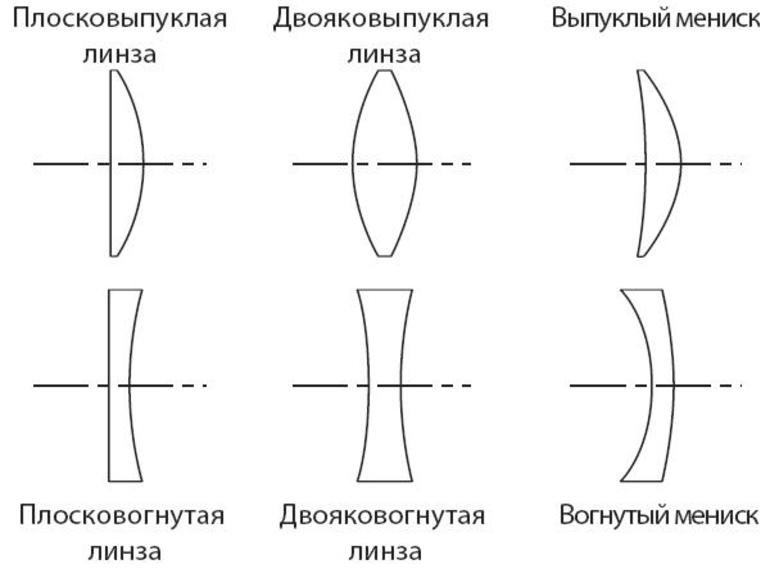
Существует огромное многообразие оптических линз. Однако все они могут быть сгруппированы по определенным физическим критериям:

При изучении физических свойств оптических стекол пользуются их упрощенным изображением. Выпуклые линзы показывают в виде отрезка со стрелками на его концах, обращенными наружу. Для рассеивающих стекол эти стрелки обращены внутрь.

Существует еще один критерий, который определяет характер прохождения лучей через рассматриваемые типы объектов. Речь идет о сравнении показателей преломления вещества и окружающей среды. Предполагают, что это значение для оптического объекта n’ больше, чем для среды n (n’>n). Для воздуха n=1, поэтому n’ должен быть больше 1.

Основная формула

Существует выражение, которое позволяет определить любую характеристику оптического стекла. Оно называется фундаментальная формула линзы. Иногда его также называют уравнением изготовителя оптических стекол. Это выражение устанавливает четкую связь между расстоянием от объекта s и его изображения s’ и показателями преломления вещества линзы и окружающей среды, а также радиусами кривизны R1, R2. Сформулировать его можно так:

n/s’ — n/s = (n’-n)*(1/R1 — 1/R2).

Фундаментальное уравнение можно найти самостоятельно, если рассмотреть преломление одного луча через каждую из искривленных поверхностей. Это выражение справедливо для всех типов рассматриваемых объектов.

Понятие о фокусе

Когда изучают тонкие оптические стекла, то особое внимание уделяют фокусному расстоянию предмета f и его изображения f’. Определения этих величин следующие:

Учитывая определения фокусных расстояний предмета и его изображения, а также привлекая фундаментальное уравнение, можно записать следующую взаимосвязь между f и f’:

Полученные выражения можно использовать для выведения гауссового вида формулы тонкой линзы. Она имеет следующую форму:

Это выражение справедливо для любых сред, а не только для воздуха. Оно также называется формулой фокусного расстояния линзы.

Гауссова форма

Ее использование позволяет сделать несколько важных выводов. Для их получения удобно переписать ее в следующем виде:

Источник

Формула тонкой линзы

теория по физике 🧲 оптика

Формула тонкой линзы — формула, связывающая три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы.

Вывод формулы

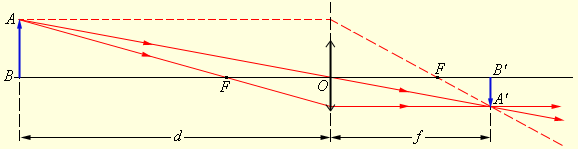
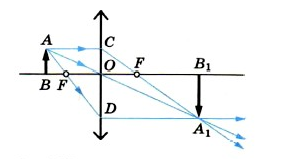
Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:

Видно, что треугольники АОВ и А₁В₁О подобные (по двум углам). Следовательно:

По двум углам также являются подобными треугольники COF и FA₁B₁. Отсюда делаем вывод, что:

Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:

Отсюда следует, что:

B O является расстоянием от предмета до линзы. Обозначим его за d. O B 1 является расстоянием от линзы до изображения. Обозначим его за f. O F является фокусным расстоянием линзы. Обозначим его за F. F B 1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:

Избавимся от знаменателей и получим:

Или можно записать так:

Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:

Формула тонкой линзы

Поскольку величиной, равной обратной фокусному расстоянию, является оптическая сила, формулу тонкой линзы можно записать следующим образом:

Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.

Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.

Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.

Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.

Применим формулу тонкой линзы:

Умножим выражение на 150d:

Увеличение линзы

Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.

Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А₁В₁ равна Н, то:

Мы уже выяснили, что треугольники АОВ и ОА₁В₁ подобны. Поэтому:

Где H — высота изображения предмета, h — высота самого предмета.

Отсюда вытекает, что увеличение линзы равно:

Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?

Сначала применим формулы тонкой линзы:

Она необходима, чтобы выразить фокусное расстояние линзы:

Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:

Отсюда это расстояние равно:

Подставим полученное выражение в формулу фокусного расстояния линзы:

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Источник

Формула тонкой линзы

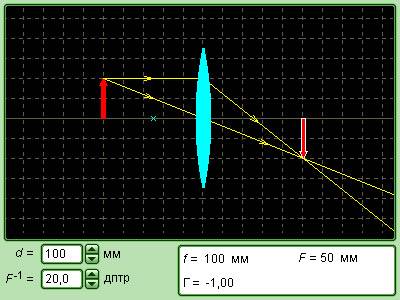
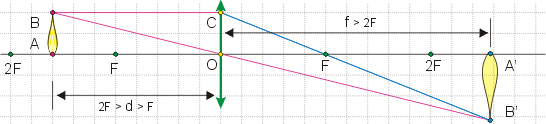
Установим соответствие между геометрическим и алгебраическим способами описания характеристик изображений, даваемых линзами. Сделаем чертёж по рисунку со статуэткой в предыдущем параграфе.

Поясним наши обозначения. Фигура AB – статуэтка, которая находится на расстоянии d от тонкой собирающей линзы с центром в точке О. Правее располагают экран, на котором A’B’ – изображение статуэтки, наблюдаемое на расстоянии f от центра линзы. Точками F обозначены главные фокусы, а точками 2F – двойные фокусные расстояния.

Почему мы построили лучи именно так? От головы статуэтки параллельно главной оптической оси идёт луч BC, который при прохождении линзы преломляется и проходит через её главный фокус F, создавая луч CB’. Каждая точка предмета испускает множество лучей. Однако при этом луч BO, идущий через центр линзы, сохраняет направление из-за симметрии линзы. Пересечение преломлённого луча и луча, сохранившего направление, даёт точку, где будет изображение головы статуэтки. Луч AO, проходящий через точку О и сохраняющий своё направление, позволяет нам понять положение точки A’, где будет изображение ног статуэтки – на пересечении с вертикальной линией от головы.

Предлагаем вам самостоятельно доказать подобие треугольников OAB и OA’B’, а также OFC и FA’B’. Из подобия двух пар треугольников, а также из равенства OC=AB, имеем:

Последняя формула предсказывает соотношение между фокусным расстоянием собирающей линзы, расстоянием от предмета до линзы и расстоянием от линзы до точки наблюдения изображения, в которой оно будет отчётливым. Чтобы эта формула была применима и для рассевающей линзы, вводят физическую величину оптическая сила линзы.

Поскольку фокус собирающей линзы всегда действительный, а фокус рассеивающей линзы всегда мнимый, оптическую силу определяют так:

Другими словами, оптическая сила линзы равна обратному значению её фокусного расстояния, взятому с «+», если линза собирающая, и взятому с «–», если линза рассеивающая. Единица оптической силы – диоптрия (1 дптр = 1/м). С учётом введённого обозначения получим:

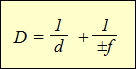D – оптическая сила линзы, дптр d – расстояние от предмета до линзы, м f – расстояние от линзы до изображения, м

Это равенство называют формулой тонкой линзы. Опыты по её проверке показывают, что она справедлива только в том случае, если линза относительно тонкая, то есть её толщина в средней части мала по сравнению с расстояниями d и f. Кроме того, если изображение, даваемое линзой, мнимое, перед величиной f необходимо использовать знак «–».

Задача. Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?

Решение. Поскольку оптическая сила линзы положительна, следовательно, линза является собирающей. Определим её фокусное расстояние:

F = 1/D = 1 : 2,5 дптр = 0,4 м, что больше, чем F.

Поскольку F Опубликовано в разделах: 9 класс, Введение в оптику

Источник

Формула тонкой линзы

Г=H/h=f/d

Также из по­до­бия тре­уголь­ни­ков CFO и A’FB’ сле­ду­ет, что:

Те­перь мы можем при­рав­нять по­лу­чен­ные ра­вен­ства, про­из­во­дим неслож­ные ариф­ме­ти­че­ские вы­чис­ле­ния и по­лу­ча­ем ко­неч­ную фор­му­лу:

1/d=1/F-1/f

Дво­я­ко­во­гну­тая линза

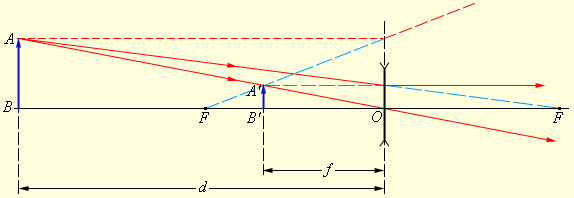
Дво­я­ко­во­гну­тую линзу, из­го­тов­лен­ную из ма­те­ри­а­ла с ко­эф­фи­ци­ен­том пре­лом­ле­ния боль­шим 1, на­зы­ва­ют рас­се­и­ва­ю­щей. Такое на­зва­ние обу­слов­ле­но тем, что лучи, иду­щие до пре­лом­ле­ния в линзе па­рал­лель­но ее глав­ной оп­ти­че­ской оси, после пре­лом­ле­ния от­кло­ня­ют­ся от сво­е­го на­прав­ле­нию в сто­ро­ну от глав­ной оп­ти­че­ской оси, в от­ли­чие от со­би­ра­ю­щей линзы. Все утвер­жде­ния о ходе лучей в рас­се­ва­ю­щей линзе яв­ля­ют­ся ана­ло­га­ми для со­от­вет­ству­ю­щих утвер­жде­ний в со­би­ра­тель­ной линзе с той лишь раз­ни­цей, что те­перь го­во­рить стоит не о ходе самих лучей, а об их про­дол­же­ни­ях.

1. Луч, про­хо­дя­щий через оп­ти­че­ский центр, не пре­лом­ля­ет­ся

2. Луч, па­рал­лель­ный глав­ной оп­ти­че­ской оси, после пре­лом­ле­ния идет так, что его про­дол­же­ние про­хо­дит через глав­ный фокус

Луч, па­рал­лель­ный по­боч­ной оп­ти­че­ской оси, после пре­лом­ле­ния идет так, что его про­дол­же­ние про­хо­дит через по­боч­ный фокус, ко­то­рый яв­ля­ет­ся точ­кой пе­ре­се­че­ния по­боч­ной оп­ти­че­ской оси па­рал­лель­ной лучу с фо­каль­ной плос­ко­стью

Фор­му­ла тон­кой рас­се­ва­ю­щей линзы будет иметь вид:

По­лу­чен­ная фор­му­ла яв­ля­ет­ся фор­му­лой тон­кой линзы, как мы видим, она свя­зы­ва­ет три ве­ли­чи­ны: рас­сто­я­ние от пред­ме­та до линзы, рас­сто­я­ние от изоб­ра­же­ния до линзы и фо­кус­ное рас­сто­я­ние линзы. Зная два из выше при­ве­ден­ных па­ра­мет­ров, мы с лег­ко­стью можем найти тре­тий.

Важно от­ме­тить, что в за­да­чах лишь два из этих па­ра­мет­ров могут ме­нять свое зна­че­ние, а имен­но рас­сто­я­ние от пред­ме­та до линзы и рас­сто­я­ние до изоб­ра­же­ния.

Т.о. формула тонкой линзы:

Правило знаков

Величины d, f, F могут быть как положительными, так и отрицательными. Если линза собирающая, то ее фокус действительный, и перед членом «1/|F|» ставиться знак «+». В случае рассеивающей линзы F больше 0 и в правой части формулы будет стоять отрицательная величина «-1/|F|». Перед членом «1/|f|» ставиться знак «плюс», если изображение действительное, и знак «минус» в случае мнимого изображения. Наконец, перед членом «1/|d|» ставят знак «плюс» в случае действительной светящейся точки, и «минус», если она мнимая (т.е. на линзу падает сходящийся пучок лучей, продолжения которых пересекаются в одной точке).

Источник