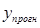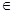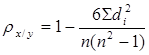Функциональная связь характеризуются тем что
Виды и формы взаимосвязей социально-экономических явлений.
Экономические данные представляют собой количественные характеристики каких-либо экономических объектов или процессов. Они формируются под действием множества факторов, не все из которых доступны внешнему контролю. Неконтролируемые факторы могут принимать случайные значения из некоторого множества значений и тем самым обуславливать случайность данных, которые они определяют. Стохастическая (вероятностная) природа экономических данных обуславливает необходимость применения соответствующих статистических методов для их обработки и анализа.
Изучение действительности показывает, что вариация каждого изучаемого признака находится в тесной связи и взаимодействии с вариацией других признаков, характеризующих исследуемую совокупность единиц. Вариация уровня производительности труда работников предприятий зависит от степени совершенства применяемого оборудования, технологии, организации производства, труда и управления и других самых различных факторов.
При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обусловливающих изменение других признаков. Признаки этой первой группы в дальнейшем будем называть признаками-факторами (факторными признаками); а признаки, которые являются результатом влияния этих факторов, будем называть результативными.
Рассматривая зависимости между признаками, необходимо выделить, прежде всего, две категории зависимости: 1) функциональные и 2) корреляционные.
Функциональные связи характеризуются полным соответствием между изменением факторного признака и изменением результативной величины, и каждому значению признака-фактора соответствуют вполне определенные значения результативного признака. Функциональная зависимость может связывать результативный признак с одним или несколькими факторными признаками. Так, величина начисленной заработной платы при повременной оплате труда зависит от количества отработанных часов.
В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных. Одновременное воздействие на изучаемый признак большого количества самых разнообразных факторов приводит к тому, что одному и тому же значению признака-фактора соответствует целое распределение значений результативного признака, поскольку в каждом конкретном случае прочие факторные признаки могут изменять силу и направленность своего воздействия.
При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака.
Статистические показатели могут состоять между собой в следующих основных видах связи: балансовой, компонентной, факторной и др.
Компонентные связи показателей характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители
Важное значение компонентной связи состоит в том, что она позволяет определять величину одного из неизвестных компонентов
Факторные связи могут рассматриваться как функциональные и корреляционные.
При функциональной связи изменение результативного признака всецело зависит от изменения факторного признака :
При корреляционной связи изменение результативного признака не всецело зависит от факторного признака, а лишь частично, так как возможно влияние прочих факторов.
Особенности корреляционной статистической связи
По характеру изменений в парной корреляции выделяют прямую и обратную связь.
Корреляционные связи помогают в решении следующих задач:
· наличие или отсутствие корреляционной зависимости между изучаемыми признаками. Может быть решена на основе параллельного сопоставления (сравнения) значений х и у, при помощи группировок и построения корреляционных таблиц;
Корреляционно-регрессионный анализ подразумевает всестороннее исследование корреляционных связей. Для решения вышепоставленных задач в статистике используются различные методы и показатели (коэффициенты), различающиеся по сложности.
Использование различных методов определяется конкретной целью исследования. Для некоторых требуется только констатация факта наличия связи, а для некоторых, наиболее сложных разработаны специальные компьютерные программы.
Теория корреляции начала разрабатываться во второй половине XIX в., а особенного расцвета достигла в XX в. Основоположниками теории корреляции являются английские биометрики Гальтон и Пирсон, в России их идеи получили развитие в трудах Чупрова.
Понятие о функциональной и корреляционной связи



1. Регрессионный анализ.
2. Корреляционно-регрессионный анализ.
3. Понятие о функциональной и корреляционной связи.
Независимыми,или факторными, называют признаки, которые вызывают изменения других, связанных с ними признаков. Признаки, изменение которых под воздействием определенных факторов требуется проследить, называют зависимыми, или результативными.
При функциональной связи изменение независимых переменных приводит к получению точно определенных значений зависимой переменной.
Наиболее часто функциональные связи проявляются в естественных науках, например в механике функциональной является зависимость расстояния, пройденного объектом, от скорости его движения и т. п.
При статистической связи каждому значению независимой переменной Х соответствует множество значений зависимой переменной Y, причем не известно заранее, какое именно. Например, мы знаем, что прибыль коммерческого банка определенным образом связана с размером его уставного капитала (этот факт не подлежит сомнению). Тем не менее, нельзя вычислить точную величину прибыли при заданном значении последнего показателя, так как она зависит еще и от множества других факторов, помимо размера уставного капитала, среди которых имеются и случайные. В нашем случае, скорее всего, мы определим лишь среднее значение прибыли, которое будет получено в целом по совокупности банков со сходным объемом уставного капитала. Таким образом, статистическая связь отличается от функциональной наличием действия на зависимую переменную большого числа факторов.
Заметим, что статистическая связь проявляется лишь «в общем и среднем» при большом числе наблюдений за явлением. Так, интуитивно мы можем предполагать, что существует зависимость между объемом основных фондов предприятия и получаемой им прибылью, а именно с увеличением первого размер прибыли возрастает. Но на это можно возразить и привести пример предприятия, обладающего достаточным количеством современного производственного оборудования, но тем не менее терпящего убытки. В данном случае мы имеем наглядный пример статистической связи, которая проявляется лишь в больших совокупностях, содержащих десятки и сотни единиц в отличие от функциональной, подтверждающейся для каждого наблюдения.
Корреляционной является статистическая связь между признаками, при которой изменение значений независимой переменной Х приводит к закономерному изменению математического ожидания случайной величины Y.
Пример 8.1 – Предположим, что имеются данные по предприятиям о размере нераспределенной прибыли предыдущего года, объеме инвестиций в основной капитал и о суммах, выделенных на приобретение ценных бумаг (тыс. ден. ед.) – таблица 8.1.
Таблица 8.1 – Основные показатели деятельности предприятий
Проведение корреляционно-регрессионного анализа предполагает решение следующих задач:
1) выявление из большого числа факторов наиболее информативных, оказывающих более существенное воздействие на результативную величину (предварительный анализ, базирующийся на простейших методах выявления зависимостей и экспертных оценках);
2) определение направления и количественной оценки тесноты зависимости между факторной величиной Х и результативной Y (при этом факторных переменных может быть достаточно много, тогда определяется множественная корреляция);
3) нахождение математической функции, описывающей зависимость результативного показателя Yот наиболее информативных факторных Х. Эта функция выполняет роль модели, которая аналитически выражает зависимость условного среднего значения результативного признака от факторных переменных
4) оценка качества полученной модели, определение возможной величины ошибки получаемых по этой модели прогнозных значений Y;
5) построение прогнозов.
Проблема направленности функциональных связей
Вы будете перенаправлены на Автор24
Понятие функциональных связей
Связь – это одна из философских категорий, выражающая взаимообусловленность существования явлений, разделенных в пространстве и времени, а также непосредственно отношения между субъектами, проявляющиеся в том, что состояния или свойства любого из них могут измениться при изменении состояний и свойств других.
Беспричинных явлений не бывает. Однако это совсем не значит, что все связи между явлениями в окружающем мире являются причинно-следственными. Казуальность – это самый существенный и всеобщий, но при этом далеко не единственный тип детерминации. Вместе с казуальностью и при относительном единении с нею, обнаруживаются и такие довольно существенные типы детерминации, как:
Следует отметить, что рассмотрение обозначенных типов детерминации свойственно только для постклассической науки и постклассической философии. Это объясняется тем, что в классической науке, а значит и в философии главенствовал лапласовский детерминизм с его абсолютизацией динамической однозначной причины явления.
Функциональная связь – это такие отношения между объектами, при которых изменения каждого из них соответствуют друг другу. Именно соответствуют, а не причиняются друг другу. Как правило, объекты, которые находятся между собой в функциональных взаимодействиях, связаны генетически, то есть каузально, только в том смысле, что являются производными от одного и того же основания. В самой же функциональной связи объектов нет главных признаков причинно-следственной связи:
Готовые работы на аналогичную тему
Причинная и функциональная связь
Один из путей проникновения в причинные связи – исследование функциональных связей. Так, выяснение причин изменения электрической проводимости металла потребовало установить функциональную зависимость, например, между температурой и электрической проводимостью. Познание причин болезней связывают с уяснением нарушений соответствующих функций организма.
Функциональная связь – это определенная зависимость явлений, при которой изменение одного явления сопровождает изменение другого.
В самом простом случае это можно выразить в математическом виде следующей формулой х = f(у), где у – переменная, именуемая функцией переменной х, если при этом каждому значению х будет соответствовать определенное значение у.
Например, для экономики важнейшими функциональными связями выступают связи между накоплением и потреблением, национальным доходом и капитальными вложениями, между производством средств и производством предметов потребления.
Благодаря функциональным зависимостям можно выразить закономерные связи сосуществующих свойств и явлений. В таком случае имеет место явление обратимости, то есть возможности переставлять местами независимые переменные и зависимые от них функции. Например, соотношение радиуса и площади круга, давления и объема газа в замкнутом сосуде. Через функциональные связи можно также описать законы, которым характерна необратимость связей. Функциональный подход является наиболее важным, когда в качестве предмета изучения рассматриваются процессы, внутренний причинный механизм которых пока неизвестен и выступает в качестве своего рода «чёрного ящика». Когда же требуется объяснить какое-либо явление, необходимо ставить вопрос о его причине. В науках, особенно в естествознании, принято выделять несколько типов причин:
Полная причина – это совокупность всех событий, при наличии которых появляется следствие. Установить полную причину можно только для достаточно простых событий, в которых принимают участие относительно небольшие группы элементов. Обычно исследование направляется на раскрытие специфических причин события.
Специфическая причина – это совокупность определенного количества обстоятельств, взаимодействием которых вызывается следствие. При этом специфическими причинами вызывается следствие, если есть ряд других обстоятельств, которые уже были в этой ситуации до того, как наступило следствие. Эти обстоятельства составляют условия действия специфической причины.
Иногда бывает так, что причиной события являются сразу несколько обстоятельств, каждое из которых необходимо, но недостаточно, чтобы наступило явление.
Главная причина – это та, которая из всей совокупности причин играет решающую роль.
Также выделяют внутренние и внешние причины. Внутренние причины работают, не выходя за рамки данной системы, а внешней причиной характеризуется взаимодействие одной системы с другой.
Например, развитие любого производства – это внутренняя причина развития человеческого общества.
Существенное значение имеют и внешние причины, например, взаимодействие организма со средой, общества с природой, взаимоотношения между государствами. Причины делятся на объективные и субъективные.
Объективные причины осуществляются не зависимо от человеческих воли и сознания. Субъективные причины заключаются в целенаправленных действиях людей, их решимости, организованности, опыте и знаниях. Необходимо отличать непосредственную причину, то есть вызывающие и определяющие данное действие, и причины опосредованные, вызывающие и определяющие действие через несколько промежуточных звеньев.
Например, при получении человеком сильной психической травмы, ее действие может не сразу проявиться. Однако через несколько лет, при действии соответствующих условий, влияние этой травмы проявилось посредством определенного симптома болезни. Это и будет опосредованной причиной.
Виды и формы связей, изучаемых в статистике. Задачи статистического изучения связи в торговле
Изучение стат. явлений формируется и развивается за счет действия на них многих факторов. Статистика при помощи различных методов выявляет эти факторы, определяет наличие связей и форму зависимости между ними.
Рассматривая зависимости между признаками, необходимо выделить, прежде всего, две категории зависимости: 1) функциональные и 2) корреляционные.
Функциональные связи характеризуются полным соответствием между изменением факторного признака и изменением результативной величины, и каждому значению признака-фактора соответствуют вполне определенные значения результативного признака. Функциональная зависимость может связывать результативный признак с одним или несколькими факторными признаками. Так, величина начисленной заработной платы при повременной оплате труда зависит от количества отработанных часов.
В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных. Одновременное воздействие на изучаемый признак большого количества самых разнообразных факторов приводит к тому, что одному и тому же значению признака-фактора соответствует целое распределение значений результативного признака, поскольку в каждом конкретном случае прочие факторные признаки могут изменять силу и направленность своего воздействия.
При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака. В отличие от жесткости функциональной связи корреляционные связи характеризуются множеством причин и следствий и устанавливаются лишь их тенденции. Статистические показатели могут состоять между собой в следующих основных видах связи: балансовой, компонентной, факторной и др.
Основные виды связей:
1)Балансовая связь характеризует зависимость между источником формирования ресурсов и их использованием.
(где предложение ресурса: Он – остатки на начало периода, П – поступления; использование ресурса: В – выбытие, Ок – остаток на конец периода).
2)Компонентная связь характеризует изменение стат пок-ля за счет изменения компонентов, его образующих.
(где a – результативный признак, b и с – факторные признаки).
3)Факторная связь проявляется в согласованной вариации изучаемых показателей.
X – факторный признак (признак, от которого зависит другой признак), y – результативный признак (зависит от факторного признака).
Факторные связи принято классифицировать по степени зависимости одного явления от другого:
1) функциональная связь – связь, при кот. величина результативного признака y полностью опр-ся величиной факторного признака х.
функциональная связь чаще всего встречается в технике, математике и др. точных науках.
2) корреляционная связь проявляется в масс. явлениях общественной жизни. В этом случае нет точного соответствия между х и у. Одному значению факторного признака х может соответствовать несколько значений результативного признака у, т.к. на результат признака у воздействует множество других факторных признаков.
Т.о. влияние факторного признака х проявляется лишь в общем, среднем для всей совокупности.
По направлению связи:
Прямая связь – направление изменения результативного признака совпадает с направлением изменения признака фактора, т.е. с увеличением факторного признака увеличивается и результативный и наоборот. Обратная связь – направление изменения результативного признака не совпадает с изменением факторного признака, т.е. при увеличении факторного признака результативный уменьшается и наоборот.
По форме связи:
1. Прямолинейные – с возрастанием величины факторного признака происходит непрерывное возрастание результативного признака и наоборот. Математически такая зависимость представляется уравнением прямой. График представлен в виде прямой. Эту зависимость называют линейной.
2. Криволинейные – с возрастанием величины факторного признака изменение результативного признака происходит неравномерно, направление его может даже меняться.
Связи:
-множественные (результативн признак 1, а факторных 2 и более)
Для корреляционных связей есть различия в том случае, если: исследуется связь между одним признаком – фактором и результативным признаком; исследуется связь между несколькими признаками – факторами и результативным признаком. В первом случае имеет место парная связь и парная корреляция, во втором случае многофакторная связь и множественная корреляция.
Задачи статистики по изучению связей:
1) выявить наличие связей между явлениями
2) определить направление связей
3) оценить тесноту связей
4) определить форму связей, т.е. выразить связь аналитически.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Реферат: Социально-экономические явления и методы исследования связей между ними
| Название: Социально-экономические явления и методы исследования связей между ними Раздел: Рефераты по экономике Тип: реферат Добавлен 19:53:57 24 декабря 2010 Похожие работы Просмотров: 1711 Комментариев: 19 Оценило: 3 человек Средний балл: 4.7 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рейтинг | Название предприятия | Собственный капитал, млн. руб. | Прибыль, млн. руб. |
| 1 | 2 | 3 | 4 |
| 1 | «Газпром» | 2772000 | 348400 |
| 2 | РЖД | 1851000 | 237545 |
| 3 | ОАО «Сургутнефтегаз» | 707913 | 214479 |
| 4 | РАО «ЕЭС России» | 386200 | 203448 |
| 5 | Нефтяная компания «ЛУКойл» | 222156 | 126326 |
| 6 | ГМК «Норильский никель» | 208143 | 118159 |
| 7 | ТНК-ВР | 165000 | 110400 |
| 8 | «Связьинвест» | 167572 | 95700 |
| 9 | Нефтяная компания «Сибнефть» | 153000 | 84800 |
| 10 | АФК «Система» | 150844 | 76503 |
| 11 | Сбербанк России | 148000 | 62929 |
| 12 | “Татнефть” | 103653 | 36876 |
| 13 | «Северсталь» | 103275 | 34312 |
| 14 | Нефтегазовая компания «Славнефть» | 101270 | 29923 |
| 15 | Евраз Груп | 77558 | 29517 |
| 16 | «Русал» | 75600 | 28512 |
| 17 | АК «Транснефть» | 46629 | 4608 |
| 18 | АвтоВАЗ http://www.tatneft.ru/ | 43308 | 1400 |
| 19 | Магнитогорский металлургический комбинат | 28500 | 1345 |
На основании имеющихся данных найдем:
Получили, что коэффициенты регрессии а = 51,61 и b = 0,115. Таким образом, уравнение зависимости прибыли предприятий (У) от величины собственного капитала (Х) имеет вид: У = 51,61 + 0,115Х, т.е. при увеличении размера собственного капитала на 1 млн. руб. прибыль предприятий в среднем увеличивается на 115 тыс. руб.
Коэффициент корреляции rху = 0,867 свидетельствует о сильной и прямой связи между размером собственного капитала и прибылью организации.
Изобразим графически исходные данные о прибыли и размере собственного капитала и полученную прямую зависимости данных признаков.
5. Анализ и прогнозирование экономических показателей на основе регрессионных моделей
Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений зависимой переменной.
Прогнозируемое значение переменной 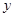
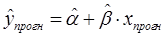
ожидаемой величины фактора 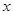
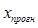
Вероятность реализации точечного прогноза теоретически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой надежностью.
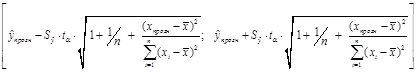
6. Измерение связей неколичественных переменных
Методы корреляционного и дисперсионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических методов.
Между тем в статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили название непараметрических.
Оценить тесноту связи между признаками можно с помощью коэффициентов взаимной сопряженности и коэффициентов контингенции или ассоциации.
В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности по значению признака называется ранжированием. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д.
При ранжировании каждой единице совокупности присваивается ранг, т. е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Например, если у 5-й и 6-й единиц совокупности значения признаков одинаковы, обе получат ранг, равный (5 + 6) / 2 = 5,5.
Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена (р) и Кендэлла ( X ). Эти методы применимы не только для качественных, но и для количественных показателей, особенно при малом объеме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.
Сущность метода Спирмена (Spearman) состоит в следующем:
1) располагают варианты факторного признака по возрастанию — ранжируют единицы по значению признака X;
2) для каждой единицы совокупности указывают ранг с точки зрения результативного признака У.
Если связь между признаками прямая, то с увеличением ранга признака X ранг признака У также будет возрастать; при тесной связи ранги признаков X и У в основном совпадут. При обратной связи возрастанию рангов признака X будет, как правило, соответствовать убывание рангов признака У. В случае отсутствия связи последовательность рангов признака У не будет обнаруживать никакого порядка возрастания или убывания.
Теснота связи между признаками оценивается ранговым коэффициентом корреляции Спирмена ( в случае, когда нет связанных рангов):
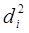
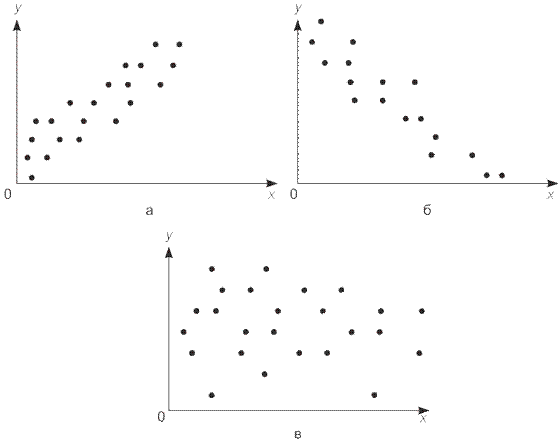
n – число наблюдений ( число пар рангов).
Коэффициент корреляции Спирмена принимает значение в интервале (-1,+1). Чем ближе он к единице, тем более тесня связь между признаками. Знак коэффициента показывает направление связи.
2. Громыко Г.Л. Теория статистики: учеб. – М., Изд-во Инфра-М, 2000.
5. Шмойлва Р.А. Практикум по теории статистики: учеб. пособ. – М., Изд-во Финансы и статистика, 2002.
- Функциональная рентгенография поясничного отдела позвоночника что
- Функциональная спондилография поясничного отдела позвоночника что это такое




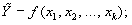
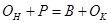
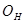 — остаток на начало отчетного периода;
— остаток на начало отчетного периода;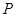 — поступление за период;
— поступление за период;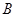 — выбытие в изучаемом периоде;
— выбытие в изучаемом периоде;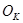 — остаток на конец отчетного периода.
— остаток на конец отчетного периода.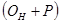 ,
,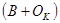
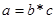
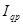 представляет произведение двух компонентов, на пример, — индекса товарооборота в сопоставимых ценах
представляет произведение двух компонентов, на пример, — индекса товарооборота в сопоставимых ценах 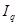 и индекса цен
и индекса цен 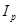 , т.е.
, т.е.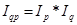
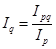 или
или 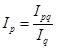
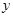 всецело зависит от изменения факторного признака
всецело зависит от изменения факторного признака 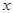 :
: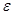 :
: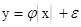
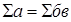 ). Индексный метод анализа позволяет определить роль отдельных компонентов в совокупном изменении сложного явления.
). Индексный метод анализа позволяет определить роль отдельных компонентов в совокупном изменении сложного явления.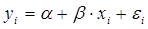 ,
,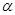 — постоянная величина (или свободный член уравнения),
— постоянная величина (или свободный член уравнения), 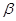 — коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Это показатель, характеризующий изменение переменной
— коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Это показатель, характеризующий изменение переменной 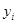 , при изменении значения
, при изменении значения 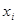 на единицу. Если
на единицу. Если 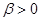 — переменные
— переменные 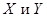 связаны линейной зависимостью, т.е.
связаны линейной зависимостью, т.е.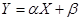 .
.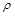 является выборочный парный коэффициент корреляции:
является выборочный парный коэффициент корреляции: 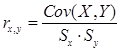 =
= 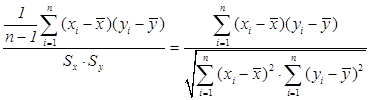 , (3.3)
, (3.3)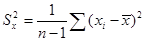
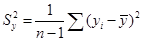
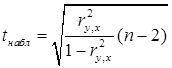 (3.4)
(3.4)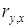 близко к нулю, связь между переменными слабая. Если случайные величины связаны положительной корреляцией, это означает, что при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать. Если случайные величины связаны отрицательной корреляцией, это означает, что при возрастании одной случайной величины, другая имеет тенденцию в среднем убывать.
близко к нулю, связь между переменными слабая. Если случайные величины связаны положительной корреляцией, это означает, что при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать. Если случайные величины связаны отрицательной корреляцией, это означает, что при возрастании одной случайной величины, другая имеет тенденцию в среднем убывать.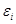 представляет собой отклонение фактического значения зависимой переменной от значения данной переменной, полученное расчетным путем:
представляет собой отклонение фактического значения зависимой переменной от значения данной переменной, полученное расчетным путем: 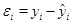 (
(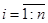 ). Если
). Если 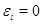 (
( ) проходит через все точки корреляционного поля, что возможно только при строго функциональной связи. Следовательно, результативный признак
) проходит через все точки корреляционного поля, что возможно только при строго функциональной связи. Следовательно, результативный признак 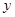 полностью обусловлен влиянием фактора
полностью обусловлен влиянием фактора 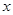 .
.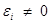 ). Величина этих отклонений и лежит в основе расчета показателей качества (адекватности) уравнения.
). Величина этих отклонений и лежит в основе расчета показателей качества (адекватности) уравнения.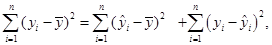 (4.2)
(4.2)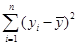
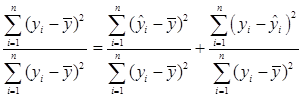
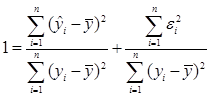 .
.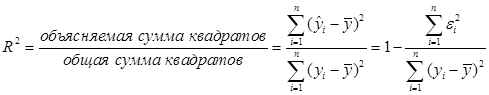 (4.3)
(4.3) к 1, тем выше качество модели.
к 1, тем выше качество модели.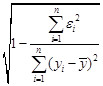 =
= 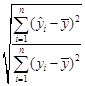 (4.4)
(4.4)
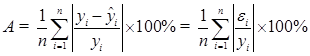 ( 4.5)
( 4.5)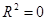 . Альтернативная ей гипотеза о значимости уравнения — гипотеза о неравенстве нулю параметров регрессии.
. Альтернативная ей гипотеза о значимости уравнения — гипотеза о неравенстве нулю параметров регрессии.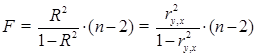 (4.6)
(4.6)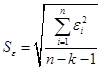 (4.7)
(4.7)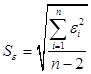
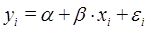
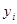 , соответствующие данным
, соответствующие данным 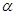 и
и 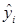 :
: 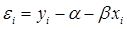 . Так как ошибки (остатки)
. Так как ошибки (остатки) 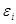 нормально распределены, то среднеквадратическое отклонение ошибок используется для измерения этой вариации. Среднеквадратические отклонения коэффициентов известны как стандартные ошибки (отклонения ):
нормально распределены, то среднеквадратическое отклонение ошибок используется для измерения этой вариации. Среднеквадратические отклонения коэффициентов известны как стандартные ошибки (отклонения ):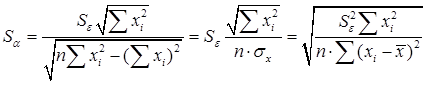
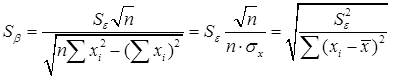 (4.8)
(4.8)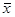 — среднее значение независимой переменной х;
— среднее значение независимой переменной х;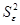 стандартная ошибка, вычисляемая по формуле (4.8);
стандартная ошибка, вычисляемая по формуле (4.8);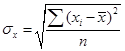 .
.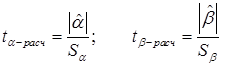 (4.9)
(4.9)